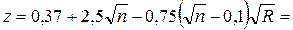Что такое гидравлический прыжок

Виды гидравлического прыжка.

Виды гидравлического прыжка.

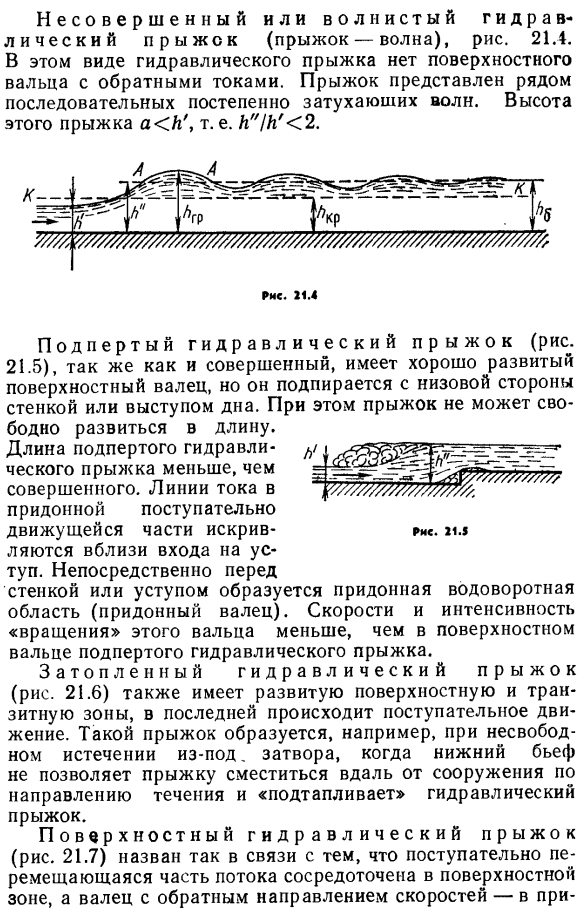
Виды гидравлического прыжка. В зависимости от условий, в которых происходит гидравлический скачок, наблюдаются его различные типы. Полный гидравлический скачок (рис. 21.3) может быть достигнут, если отсутствует вертикальное ограничение канала, например, если отношение глубины»!».К ’ ^ 2.It наблюдается в виде нижней полки. Для полного гидравлического прыжка его высота a> k’is characteristic. In этот тип скачка, поверхностного крена, выражается в обратном направлении скорости на свободной поверхности, а также в области поступательного движения жидкости (проходящей части потока). 388. Неполный или волнообразный гидравлический прыжок (скачкообразная волна), рисунок 21.4.In этот тип гидравлического скачка там никакой поверхностный барабанчик с обратной подачей. Скачки представлены серией волн, которые затухают непрерывно и постепенно.

В зависимости от условий, в которых происходит гидравлический прыжок, наблюдаются различные его виды. Людмила Фирмаль

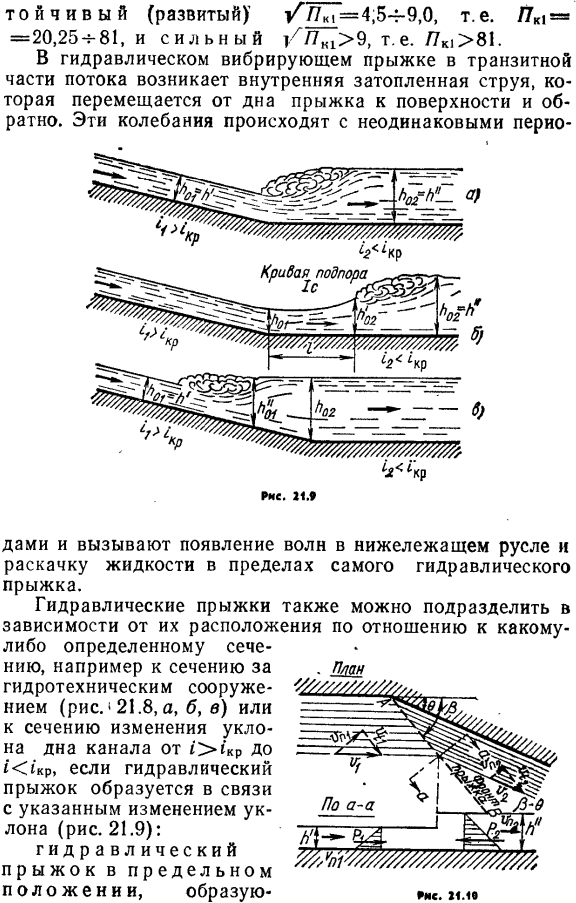
В гидравлическом вибрирующем прыжке в транзитной части потока возникает внутренняя затопленная струя, которая перемещается от дна прыжка к поверхности и обратно. Людмила Фирмаль

Смотрите также:

Возможно эти страницы вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

ГИДРАВЛИЧЕСКИЙ ПРЫЖОК

В системах водоотведения гидравлический прыжок образуется на очистных сооружениях при истечении потоков из-под щита и в перепадных колодцах, при изменении уклона трассы коллектора и в других случаях.

На транспортных магистралях гидравлический прыжок может иметь место в водопропускных и водоотводных сооружениях (каналы, трубы, малые мосты, перепады, быстротоки).

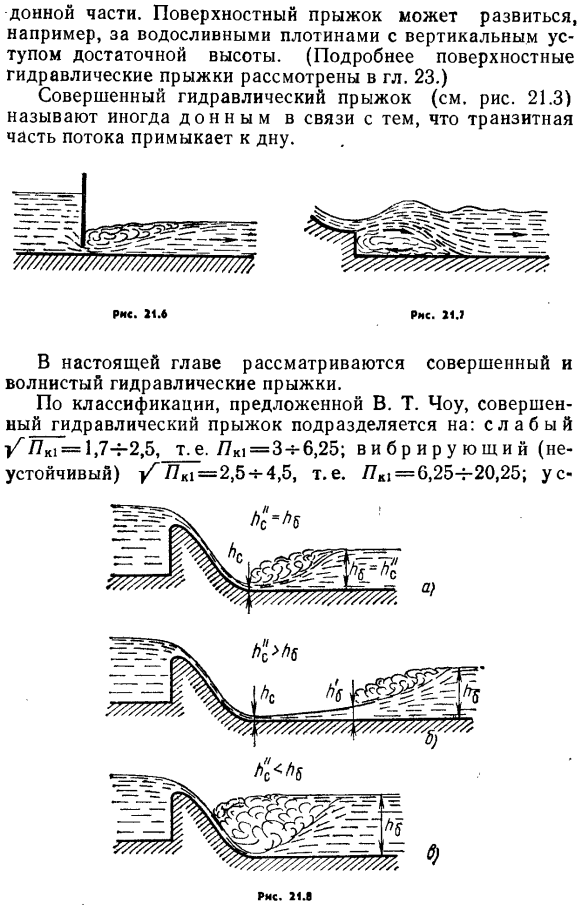
Прыжок, в котором над основанием транзитного потока образуется валец с водоворотным движением, называется совершенным гидравлическим прыжком.

Рис. 8.13. Совершенный гидравлический прыжок

При истечении из-под щита потенциальная энергия жидкости перед щитом переходит в кинетическую энергию вытекающей струи. За счет большой скорости истечения сразу за щитом поток в начале прыжка находится в бурном состоянии и глубина его . Бурный поток вливается в поток, находящийся в спокойном состоянии, с глубиной , равной глубине в конце прыжка.

В результате образования прыжка наблюдается поверхность раздела между транзитной струей и вальцем, представленная на рис. 8.13 линией ABC. После точки А транзитный поток расширяется от глубины , до глубины . Глубины воды в прыжке .

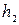
В вальце происходит вращательное движение жидкости, при этом он насыщен пузырьками воздуха. Верхняя поверхность вальца имеет волнообразную форму.

В транзитной струе, расположенной под вальцем, происходит движение жидкости. Гидравлический прыжок можно рассматривать как затопленную полуограниченную струю, вытекающую из отверстия в однородную жидкость. Такой подход к рассмотрению прыжка позволяет несколько лучше представить физическую модель прыжка, в которой транзитный растекающийся поток является основным участком струи. В зоне поверхности раздела между вальцами и транзитным потоком, за счет пульсации скоростей и давления происходит интенсивный массобмен частичками жидкости.

За гидравлическим прыжком осуществляется выравнивание эпюры скоростей, и окончательно эпюра скорости приобретает форму, соответствующую равномерному установившемуся движению потока в открытом русле. Участок от прыжка до сечения, в котором эпюра скорости выравнивается, называется послепрыжковым, а длина этого участка обозначается .

Следует отметить, что на участке вальца за счет вихреобразования имеют место наибольшие скорости у дна русла и они уменьшаются на послепрыжковом участке.

Рассмотрим совершенный гидравлический прыжок (рис. 8.13), считая длину прыжка достаточно малой и уклон дна русла 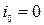. Сечение русла на участке прыжка постоянно и может иметь любую форму. Расход жидкости равен Q.

Изменение проекции количества движения на ось х за время dt равно разности количества движения массы объемов A’b’d’C’ и AbdC.

Следовательно, изменение количества движения

. (8.45)

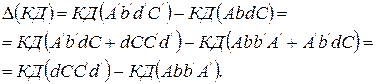
Массе жидкости, проходящей через сечение 2—2, соответствует масса объема dCC’d’ и равняется массе жидкости объема Abb’А’ первого сечения. Масса

.

Изменение количества движения

, (8.46)

где и — средние скорости в сечениях 2—2 и 1—1.

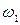
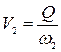
Средние скорости в сечениях с площадями живого сечения и

и .

Изменения количества движения за время dt

. (8.47)

Определим сумму проекций на ось х импульсов сил, действующих на объем жидкости AbdC, за тот же промежуток времени.

Для этого принимаем следующие допущения:

• считаем, что в сечениях 2—2 и 1—1 движение плавно изменяющееся;

Для плавно изменяющегося движения гидростатический напор в любой точке взятого сечения постоянен, т.е. соблюдается распределение давления по гидростатическому закону. Поэтому силы давления , и находятся по формулам гидростатики:

; , (8.48)

где , и — погружение центров тяжести сечений соответственно площадей , и , они отсчитываются от свободной поверхности в соответствующих сечениях. Сумму проекций импульса сил (ИС) за время dt можно представить в виде

. (8.49)

Изменение количества движения равно импульсу сил:

. (8.50)

После некоторых упрощений и перестановок в (8.50) получим основное уравнение гидравлического прыжка

. (8.51)

При заданном расходе левая часть уравнения (8.51) является функцией глубины , так же как и правая часть уравнения. Для любого сечения в пределах гидравлического прыжка можно записать

. (8.52)

Функция называется прыжковой функцией, и (8.51) можно выразить в следующем виде:

, (8.53)

где и — функции, соответствующие глубинам в русле , и .

Используя свойство, что прыжковые функции равны, можно найти одну из глубин, если другая известна. Решение этой функции показывает, что при критической глубине она имеет минимальное значение.

На рис. 8.14 изображен график прыжковой функции, построенной согласно зависимости (8.52).

Рис. 8.14. График прыжковой функции

На рис. 8.14 приведена кривая удельной энергии сечения .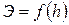

График этой функции подобен графику функции удельной энергии сечения , но минимальное значение рассматриваемой функции значительно меньше минимального значения удельной энергии сечения. Поэтому график функции более вытянутый к оси , чем функции .

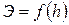
Исследование графика прыжковой функции позволяет сделать следующие выводы:

· глубины в начале , и конце прыжка имеют равные значения прыжковой функции, и такие глубины называют сопряженными глубинами;

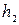
· изменение глубины в начале прыжка ведет к изменению глубины в его конце, причем эта зависимость обратная. Увеличение глубины , приводит к уменьшению глубины .

Источник

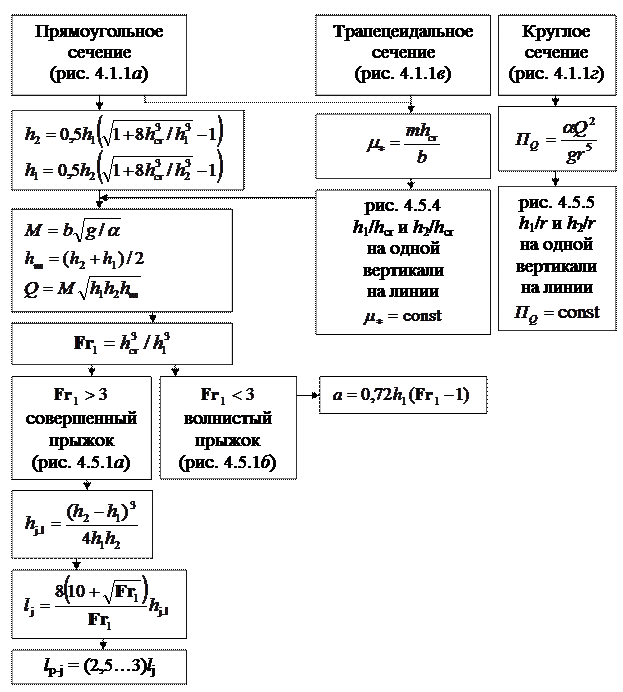
ТЕМА 4.5. Гидравлический прыжок

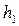
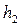
• Гидравлический прыжок – это резкий скачкообразный переход от бурного состояния к спокойному, т.е. переход от глубин, меньших критической, к глубинам, большим критической. Глубины перед прыжком и после него называются взаимными или сопряженными. В зависимости от соотношения взаимных глубин прыжок бывает совершенным (рис. 4.5.1а) или волнистым (рис. 4.5.1б).

а б

Рис. 4.5.1. Совершенный а и волнистый б гидравлические прыжки.

• Совершенный гидравлический прыжок – это прыжок, в котором над основной транзитной струей образуется участок с водоворотным движением (поверхностный валец).

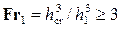
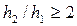
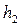
• В руслах прямоугольного сечения совершенный прыжок образуется, если число Фруда , или если отношение взаимных глубин . При этом вторая глубина берется на некотором расстоянии от водоворота, в сечении, где заканчивается повышение глубин.

• Импульс жидкости, проходящей за единицу времени через сечение потока,

, (4.5.1)

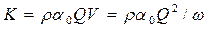
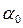
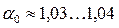
где – корректив импульса (коэффициент Буссинеска), учитывающий неравномерность распределения скоростей по сечению ( ).

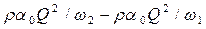
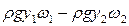
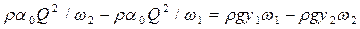
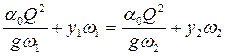
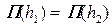
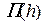
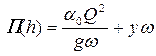
• Согласно основному закону динамики изменение импульса жидкости между сечениями 1–1 и 2–2 (рис. 4.5.2) за единицу времени равняется равнодействующей силе, – в данном случае силе гидростатического давления , где y – глубина погружения центра тяжести сечения. Таким образом . Отсюда получаем основное уравнение гидравлического прыжка:

; , (4.5.2)

где – прыжковая функция:

. (4.5.3)

Рис. 4.5.2. Взаимные (сопряжённые) глубины.

• Прыжковые функции сопряженных глубин равны между собой.

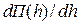
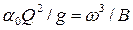
• Приравняв производную прыжковой функции нулю, после ряда преобразований получаем условие минимума прыжковой функции:

. (4.5.4)

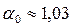
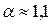
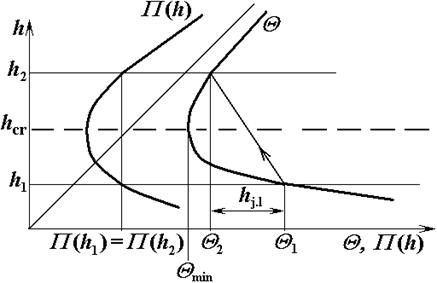Это уравнение отличается от уравнения (3.2) для определения критической глубины тем, что в одном стоит корректив импульса , а в другом корректив кинетической энергии . Поскольку , можно считать, что минимум прыжковой функции соответствует минимуму удельной энергии сечения (рис. 4.5.3), т.е. критической глубине.

Рис. 4.5.3. Прыжковые функции сопряжённых глубин равны.

• График рис. 4.5.3 дает возможность объяснить причину резкого увеличения глубин в гидравлическом прыжке. В самом деле, если глубины будут повышаться постепенно, как при плавноизменяющемся движении, то в соответствии с ними постепенно будет изменяться и удельная энергия сечения. Сначала она будет уменьшаться от Θ₁ до Θ_min, а потом будет увеличиваться от Θ_min до Θ₁, но это противоречит закону сохранения энергии.

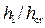
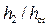
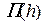
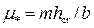
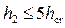
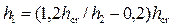
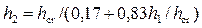
• Для гидравлического прыжка в руслах трапецеидального сечения относительные взаимные глубины и находят по графику Рахманова (рис. 4.5.4) при одинаковых значениях прыжковой функции и параметра . Приближенно при взаимные глубины в руслах трапецеидального сечения можно определить по эмпирическим формулам Рахманова:

, (4.5.5)

. (4.5.6)

• Для прямоугольного русла

, (4.5.7)

. (4.5.8)

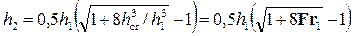
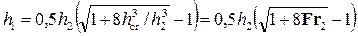
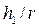
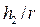
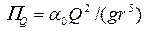
• Относительные взаимные глубины прыжка и в круглых безнапорных трубах систем водоотведения находят по графику рис. 4.5.5 при одинаковых значениях относительной прыжковой функции и расходного параметра трубы .

• Гидравлический прыжок сопровождается потерями энергии, вызванными внутренним трением при вращении жидкости в поверхностном вальце. Если уклон дна незначителен, потери удельной энергии в прыжке (рис. 4.5.3)

. (4.5.9)

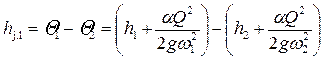
Для русел прямоугольной формы

. (4.5.10)

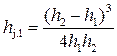
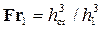
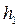
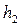
• Чем больше число Фруда в сечении до прыжка, т.е. чем меньше глубина до прыжка, тем большей будет глубина после прыжка и тем большими будут потери энергии в прыжке.

Пример 4.5.1. Определить потери удельной энергии в гидравлическом прыжке трапецеидального сечения, если сопряженные глубины до и после прыжка равны: h₁ = 0,4 м, h₂ = 0,8 м, а средние в сечениях скорости, соответствующие этим глубинам: V₁ = 3,6 м/с и V₂ = 1,4 м/с.

Решение. Из уравнения Бернулли потери удельной энергии между сечениями потока

0,217 м.

Рис. 4.5.4. График Рахманова для нахождения сопряжённых глубин в канале трапецеидального сечения.

Рис. 4.5.5. График для нахождения сопряжённых глубин в канале круглого сечения.

• За длину прыжка 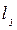берут расстояние от начала вальца до сечения, где глубины становятся практически постоянными, хотя они и дальше еще немного увеличиваются (рис. 4.5.6). В русле прямоугольного сечения

. (4.5.11)

Рис. 4.5.6. Длины прыжка и послепрыжкового участка.

Если Fr₁ > 10, можно пользоваться более простой формулой:

(4.5.12)

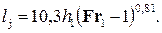
• Участок потока после прыжка, на котором переформировывается эпюра скоростей, называется послепрыжковым. Для него характерны повышенные пульсации скоростей и давлений, что создает опасность размыва. Длина послепрыжкового участка

. (4.5.13)

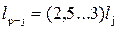
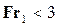
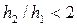
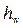
• В руслах прямоугольного сечения волнистый прыжок (рис. 4.5.7) возникает, если , что соответствует соотношению сопряженных глубин . Поверхностный валец не образовывается, а поток переходит из бурного состояния в спокойное благодаря образованию ряда волн с наибольшей глубиной .

• Высота первой волны волнистого прыжка

. (4.5.14)

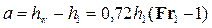
Рис. 4.5.7. Высота первой волны гидравлического прыжка.

• Отношение сопряженных глубин волнистого прыжка:

(при ), (4.5.15)

(при ). (4.5.16)

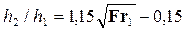
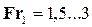
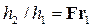
За бóльшую сопряженную глубину 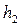волнистого прыжка принимают глубину в сечении, где волны практически затухают.

• Гидравлический прыжок в прямоугольном сечении может использоваться как водомер. Расход

, (4.5.17)

где – постоянный множитель для данного русла, – среднее арифметическое значение взаимных глубин в прыжке.

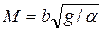
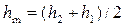
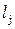
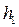
Пример 4.5.2. Определить в русле прямоугольного сечения (m = 0) глубину после прыжка h₂ и его длину , если расход Q = 1,0 м 3 /с, ширина русла b = 1 м, а глубина в начале прыжка = 0,2 м.

Решение. Критическая глубина

0,482 м/с.

14,0.

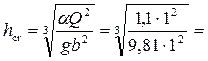
Так как 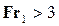, то прыжок – совершенный.

Глубина после прыжка

0,964 м.

16,4 м.

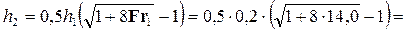
С использованием графика рис. 4.5.4 имеем

; 0,415 и 2,0.

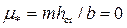
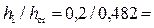
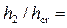
Глубина после прыжка 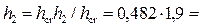0,92 м.

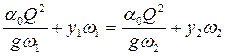
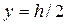
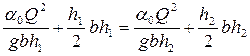
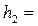
Решим ту же задачу с использованием табличного процессора Microsoft Excel (рис. 4.5.8) методом подбора из основного уравнения гидравлического прыжка . Для прямоугольного сечения глубина погружения центра тяжести сечения . Равенство удовлетворяется при 0,93 м.

Содержимое ячеек: G2 =СТЕПЕНЬ(B2*C2*C2/D2/E2/E2;1/3) H2 =СТЕПЕНЬ(G2/F2;3) I2 =0,5*F2*(КОРЕНЬ(1+8*H2)-1) D5 =A2*C2*C2/D2/E2/F2+F2/2*E2*F2 D10 =$A2*$C2*$C2/$D2/$E2/D8+D8/2*$E2*D8

Рис. 4.5.8. Решение примера 4.3.2 в MS Excel.

Рис. 4.5.9. Схема расчета гидравлического прыжка.

ТЕМА 4.6. Водосливы

• Водослив – это препятствие в потоке, которое стесняет его снизу и по бокам. Часть потока перед водосливом называется верхним бьефом, часть потока после водослива – нижним бьефом.

• Превышение отметки свободной поверхности в верхнем бьефе над отметкой порога водослива (рис. 4.6.1) называется геометрическим напором на водосливе H. Геометрический напор измеряется на расстоянии (3. 4)H от верховой грани водослива, где снижение уровня воды перед водосливом практически несущественно.

• Напор с учетом скорости подхода V₀ называется полным напором:

. (4.6.1)

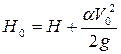
• Разность отметок свободной поверхности жидкости в верхнем и нижнем бьефах называется геометрическим перепадом на водосливе z (рис. 4.6.1). Полным перепадом на водосливе называется сумма геометрического перепада и скоростного напора перед водосливом:

. (4.6.2)

Рис. 4.6.1. Незатопленный а и затопленный б водосливы с тонкой стенкой.

• В зависимости от толщины δ порога (водосливной стенки) различают водосливы с тонкой стенкой δ 3 /с, [H] = м. Если H = 0,05…0,25 м, то α = 2,5 и M = 1,4. Если H = 0,25…0,5 м, то α = 2,47 и M = 1,343.

Рис. 4.6.5. Треугольный водослив с углом θ = 90°.

Пример 4.6.1. На канале прямоугольного сечения шириной русла b = 2 м установлен водослив с тонкой стенкой высотой P = 1 м. Определить расход Q, если напор на водосливе H = 0,65 м и глубина воды в нижнем бьефе h_d = 1,2 м (рис. 4.6.1б).

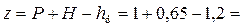
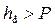
Решение. Отношение напора на водосливе к его высоте H/P = 0,65/1 = 0,65. Перепад на водосливе 0,45 м. Относительный перепад на водосливе 0,45. По графику рис. 4.6.4 критический перепад (z/P)_cr ≈ 0,75. Так как уровень воды в нижнем бьефе расположен выше порога водослива: (1,2 > 1) и относительный перепад на водосливе z/P меньше его критического значения: z/P 3 /с.

Пример 4.6.2. В канале установлен треугольный водослив с тонкой стенкой с углом при вершине θ = 90° (рис. 4.6.5). Напор на пороге водослива H = 0,5 м. Определить расход Q воды в канале.

Решение. Если H = 0,25…0,5 м, то α = 2,47 и M = 1,343.

Расход = 0,242 м 3 /с.

• Водосливы практического профиля криволинейного очертания могут быть безвакуумными и вакуумными. Безвакуумные водосливы имеют очертание (рис. 4.6.6а), совпадающее с нижней поверхностью струи, которая переливается через водослив с тонкой стенкой (очертание Кригера-Офицерова).

Если водосливная поверхность не доходит до струи (рис. 4.6.6б), то под струей устанавливается давление, меньшее атмосферного, а водослив называется вакуумным. Струя прижимается к водосливу. Один и тот же водослив может быть как вакуумным, так и безвакуумным. В самом деле, при увеличении напора на безвакуумном водосливе струя старается откинуться дальше от водослива и между ним и водосливной поверхностью образуется вакуум.

• Пропускная способность водосливов практического профиля

. (4.6.12)

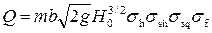
Рис. 4.6.6. Водосливы практического профиля криволинейного очертания: а – безвакуумный, б – вакуумный.

• Коэффициент расхода безвакуумного водослива m = 0,49…0,5. Вакуумные водосливы имеют большую пропускную способность, поскольку скорость потока на водосливе увеличивается в случае уменьшения давления. Коэффициент расхода вакуумного водослива может достигать значений m = 0,54…0,57.

• Коэффициент полноты напора σ_h учитывает отличие напора H на водосливе от расчетного напора H_c, по которому построено очертание водослива Кригера-Офицерова. Если H/H_c = 0,2…1, то σ_h = 0,84…1; если H/H_c = 1…2 (это уже вакуумный профиль), то σ_h = 1…1,1; если H = H_c, то σ_h = 1.

• Коэффициент формы σ_sh зависит от близости формы оголовка к очертанию Кригера-Офицерова). Обычно σ_sh = 0,85…1.

• Коэффициент бокового сжатия

, (4.6.13)

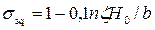
где ζ – коэффициент формы береговых опор и промежуточных быков (рис. 4.6.7); n – количество боковых сжатий, при одном отверстии водослива n = 2, при двух отверстиях n = 4 и т.д.

Рис. 4.6.7. Коэффициент формы береговых опор и промежуточных быков.

• Коэффициент затопления σ_f находят по графику рис. 4.6.8 в зависимости от отношения h_e/H₀ (см. рис. 4.6.1б). Кривая 1 принадлежит вакуумным водосливам (рис. 4.6.6б), кривая 2 – безвакуумным водосливам (рис. 4.6.6а), кривая 3 – водосливам с расширенным гребнем (рис. 4.6.9).

Рис. 4.6.8. Коэффициент затопления для водосливов: вакуумных (1), безвакуумных (2) и с широким порогом(3).

Рис. 4.6.9. Водослив с расширенным гребнем.

• Незатопленный водослив с широким порогом. В зависимости от ширины порога могут устанавливаться такие схемы протекания потока.

• При δ ≈ (2…4)H глубина потока непрерывно понижается на пороге (рис. 4.6.10б).

• При (2…4)H (8…10)H на условия протекания потока начинают влиять силы трения, т.е. пропускная способность водослива становится зависимой от потерь энергии по длине, и водослив можно рассматривать как короткий канал. В начале порога устанавливается так называемая сжатая (т.е. наименьшая) глубина h_sq и ряд волн, которые затухают с переходом через критическую глубину, которая соответствует минимальной удельной энергии сечения Θ и обозначена на рис. 4.6.11 линией К–К. Такой переход называется волнистым гидравлическим прыжком.

Рис. 4.6.11. Водослив как короткий канал с волнистым гидравлическим прыжком.

• Пропускная способность незатопленных водосливов с широким порогом

. (4.6.14)

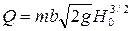
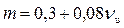
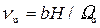
• Коэффициент расхода для водосливов с широким порогом , где ν_u – параметр сжатия потока при входе на водослив, который равняется отношению произведения ширины отверстия b водослива на величину напора H перед водосливом к площади живого сечения Ω_u в верхнем бьефе:

. (4.6.15)

Для неплавных оголовков прямоугольных подводящих русел 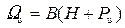, где B – ширина подводящего русла, P_u – высота водослива со стороны верхнего бьефа.

• Для нахождения глубины h на пороге водослива с широким порогом используют уравнение Бернулли для сечений, проходящих через точки A перед водосливом и C на его пороге, относительно плоскости сравнения, проведенной через верховую грань водослива (рис. 4.6.10а):

, (4.6.16)

где – коэффициент сопротивления на входе на водослив, V – скорость на пороге водослива. С учетом формул , , , а также считая, что α ≈ 1, получаем:

, (4.6.17)

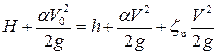
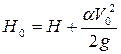
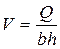
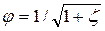
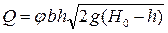
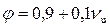
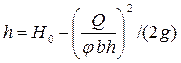
где коэффициент скорости . Отсюда

. (4.6.18)

• Затопленный водослив с широким порогом (рис. 4.6.12). Затопление происходит, если глубина подтопления (превышение отметки поверхности воды в нижнем бьефе над гребнем водослива) h_e > NH, где критерий затопления N ≈ 0,8.

• Параметр сжатия потока при выходе из водослива

, (4.6.19)

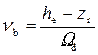
где 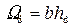– площадь живого сечения в нижнем бьефе.

• Характер течения на затопленном водосливе зависит от условий входа на него. Если вход плавный и степень подтопления значительная, на водосливе устанавливается приблизительно горизонтальная поверхность с перепадом восстановления z_r на выходе в нижний бьеф (рис. 4.6.12а). При неплавном входе на пороге образуется впадина с последующим волнистым повышением глубины (рис. 4.6.12б). Пропускная способность затопленного водослива

, (4.6.20)

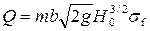
где коэффициент затопления σ_f = 0,44…1 в зависимости от степени затопления h_e/H и условий на входе (плавный или неплавный вход).

• Энергия сечения на выходе из водослива вследствие потерь напора на сопротивлении водослива ниже энергии на входе, что при спокойном состоянии потока (рис. 4.3.1) означает уменьшение глубины в нижнем бьефе по сравнению с глубиной в верхнем бьефе на величину z.

Рис. 4.6.12. Затопленный водослив с широким порогом: а – при плавном входе, б – при неплавном входе.

• В случае большой степени затопления (h_e/H ≥ 0,95) для определения пропускной способности лучше пользоваться формулой:

. (4.6.21)

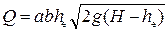
Значения поправочного коэффициента a = 0,8…2,4 в зависимости от параметра сжатия потока при выходе из водослива ν_b и условий на входе и выходе (плавные они или нет) представлены в табл. 4.6.1.

Таблица 4.6.1. Поправочный коэффициент в формуле расхода через водослив.

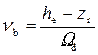	a при входе и выходе
неплавных	плавных
0,1 0,3 0,5 0,7	0,8 1,35 1,9	0,9 1,1 1,6 2,4

• Расчет отверстий водопропускных сооружений. Отверстия шлюзов-регуляторов, малых мостов и т.п. не имеют порога, и напор перед ними образуется за счет бокового сжатия русла (рис. 4.6.13).

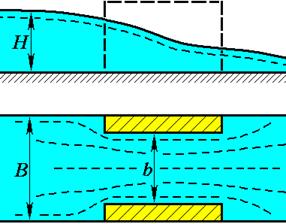Рис. 4.6.13. Водослив с боковым сжатием.

• Водомерные лотки. На очистных сооружениях (рис. 4.6.14) систем водоотвода (канализации) измерение расхода сточных вод необходимо для регулирования и контроля над работой очистных сооружений. Применение для этих целей мерных водосливов с тонкой стенкой невозможно, поскольку сточные воды будут создавать заиливание перед водосливом. Поэтому для измерения расхода сточных вод обычно применяют водомерные лотки, работающие по схеме водослива без порога (P = 0), что исключает заиливание (рис. 4.6.15). Для уменьшения потерь энергии лотки выполняют с постепенным плавным сужением к горловине и расширением после нее.

Рис. 4.6.14. Очистные сооружения.

• На рис. 4.6.15а показан лоток, работающий в условиях затопленного истечения (лоток Вентури). Расход через такой лоток (из уравнения Бернулли):

, (4.6.22)

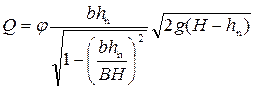
где φ – коэффициент скорости (при плавном входе φ = 0,96…0,97, при неплавном входе φ = 0,90…0,95), 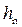– высота воды в сжатом сечении лотка, b – ширина суженной части лотка, H – глубина в канале перед входом в лоток, B – ширина канала.

Рис. 4.6.15. Водомерный лоток: а – с затопленным истечением, б – с незатопленным истечением.

• Если суженная вставка выполнена со значительным (i > i_cr) уклоном (рис. 4.6.15б), то в горловине лотка поток становится бурным, возникает гидравлический прыжок через критическую глубину и вода через лоток протекает по схеме незатопленного (свободного) водослива. В этом случае расход

(4.6.23)

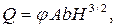
где; A – коэффициент, зависящий от отношения :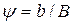

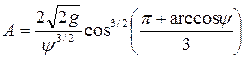
. (4.6.24)

Условие установления критической глубины в лотке:

, (4.6.25)

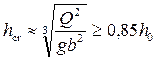
где – глубина воды при равномерном движении в канале, в котором установлен лоток.

Пример 4.6.3. В канале прямоугольного сечения шириной 1 м и с уклоном дна установлен для измерения проходящего расхода воды лоток с критической глубиной (рис. 4.6.15б). Стенки и дно канала облицованы кирпичом ( ; высота боковых стенок канала 1,3 м. Максимальный расход воды в канале 1 м 3 /с. Требуется определить ширину горловины лотка b для обеспечения условий свободного истечения.

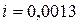
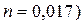
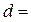
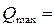
Решение. Определяем глубину воды при равномерном движении в канале в условиях максимального расхода . Задаёмся различными значениями глубин до тех пор, пока не устанавливаем, что максимальному расходу 1 м 3 /с соответствует глубина 1 м. Действительно, в этом случае:

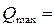
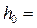
площадь живого сечения 1 м 2 ;

смоченный периметр 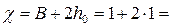3 м;

гидравлический радиус 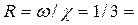0,333 м;

показатель степени в формуле скоростной характеристики

0,683;

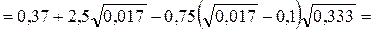
скоростная характеристика 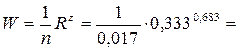27,8 м/с;

расходная характеристика 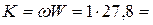27,8 м 3 /с;

расход 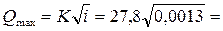1 м 3 /с.

Исходя из условия (4.6.26), минимальное значение критической глубины

0,85 м.

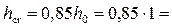
Из (4.6.25) необходимая для создания такой критической глубины ширина горловины лотка

0,44 м.

Принимаем 0,4 м; = 0,4.

1,77.

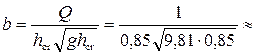
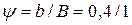
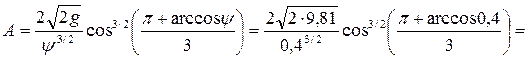
Принимаем значение коэффициента .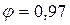

Из (4.6.24) глубина в верхнем бьефе 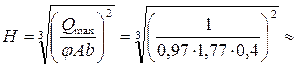1,28 м.

Эта глубина в верхнем бьефе является допустимой для подходного участка канала, так как 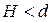(1,28 i_cr), то состояние потока в нем бурное (рис. 4.7.4), и после водослива устанавливается без гидравлического прыжка через критическую глубину кривая подпора по типу нижней кривой на рис. 4.4.1б.

• Если уклон дна нижнего бьефа меньше критического (i h_n), прыжок устанавливается на некотором расстоянии (иногда очень бол

Источник