Что такое главный период функции

Периодическая функция

Периодическая функция — это функция, значения которой не изменяются при добавлении к значениям её аргумента некоторого числа T (отличного от нуля).

Функция y=f(x) называется периодической, если существует такое число T≠0, что для любого x из области определения этой функции выполняются равенства:

Число T называют периодом функции y=f(x).

Из определения следует, что значения x-T и x+T также входят в область определения функции y=f(x).

Свойства периодических функций

1) По определению периодической функции для любого x из области определения y=f(x) если T — период функции, то f(x-T)= f(x)=f(x+T).

2) Для любого x из области определения y=f(x) если T₁ — период функции, то

Так как T₂ также является периодом функции y=f(x), то для аргумента x-T₁

Следовательно, число T₁+T₂ является периодом функции y=f(x).

3) Это свойство непосредственно вытекает из свойства 2, если T взять в качестве слагаемого n раз.

4) Если T — период функции f(x), то для аргумента kx+b

Значит число T/k — период функции f(kx+b).

5) Эти свойства следуют непосредственно из определения.

Например, для суммы f(x) и g(x):

Из свойства 3 следует, что каждая периодическая функция имеет бесконечно много периодов.

Если среди всех периодов функции y=f(x) существует наименьший положительный период, то его называют главным (или основным) периодом функции.

Примеры периодических функций

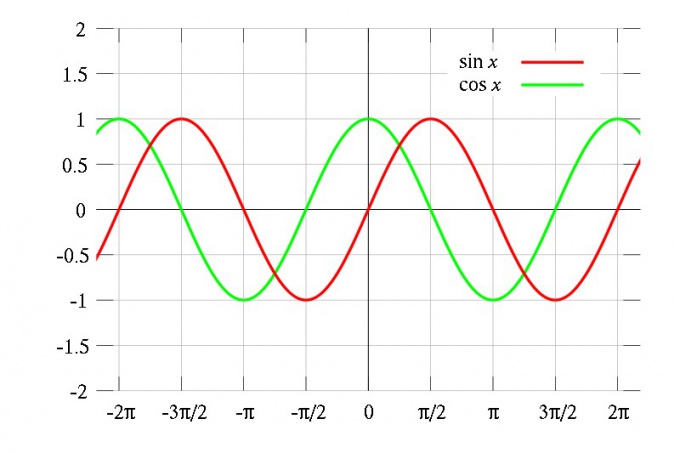
1) Поскольку для любого x выполняются равенства

то функции y=sin x и y=cos x являются периодическими с периодом T=2π.

2) Так как для любого x из области определения функции y=tg x выполняется равенство

tg (x-π)=tg x =tg (x-π), то y=tg x — периодическая функция с периодом T=π.

Аналогично, y=ctg x — периодическая функция с периодом T=π.

3) Так как для любого действительного числа x и любого рационального числа k выполняется равенство D(x+k)=D(x), то функция Дирихле D(x) — периодическая с периодом T=k, где k∈Q, k≠0.

Поскольку k — любое рациональное число, невозможно его указать наименьшее положительное значение. Следовательно, функция Дирихле не имеет главного периода.

4) Рассмотрим частный случай линейной функции y=b, b — действительное число (b∈R). Эта функция определена на множестве действительных чисел и при любых значениях аргумента принимает единственное значение y=b, то есть для любого действительного числа m (m∈R), y(x)=y(x+m)=b.

Значит y=b — периодическая функция с периодом T=m, где m∈R, m≠0.

Так как m — любое действительное число, оно не имеет наименьшего положительного значения. Поэтому функция y=b не имеет главного периода.

5) Так как для любого действительного x и любого целого k выполняется равенство =, то функция дробной части числа y= — периодическая с периодом T=k, где k∈Ζ, k≠0.

Наименьшим положительным целым числом является единица. Следовательно, T=1 — главный период функции y=.

Главный период функций y=sin x и y=cos x T=2π.

Главный период функций y=tg x и y=ctg x T=π.

Если T — период функции y=sin x, то sin (x-2π)=sin x = sin (x-2π) для любого x.

То есть любой период функции y=sin x имеет вид 2πn, n∈Z.

Наименьшее положительное значение это выражение принимает при n=1 и оно равно T=2π.

Таким образом, 2π — главный период функции y=sin x.

Аналогично доказываются утверждения о главном периоде функций y=cos x, y=tg x и y=ctg x.

Из 4-го свойства периодических функций непосредственно следует, что для функций y=sin (kx+b) и y=cos (kx+b) (k≠0) наименьший положительный период

а для функций y=tg (kx+b) и y=ctg (kx+b) (k≠0) наименьший положительный период

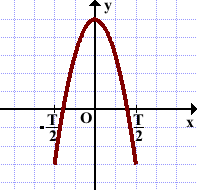
График периодической функции повторяется через промежутки длиной T (на оси Ox).

Дана часть графика

промежутке длиной T.

Чтобы построить график функции, выполняем параллельный перенос этой части графика вдоль оси Ox на ±T, ±2T,… :

Источник

Как определить периодичность функции

Если F(x) — функция аргумента x, то она называется периодической, если есть такое число T, что для любого x F(x + T) = F(x). Это число T и называется периодом функции.

Периодов может быть и несколько. Например, функция F = const для любых значений аргумента принимает одно и то же значение, а потому любое число может считаться ее периодом.

Обычно математика интересует наименьший не равный нулю период функции. Его для краткости и называют просто периодом.

Если F(x) — периодическая функция с периодом T, и для нее определена производная, то эта производная f(x) = F′(x) — тоже периодическая функция с периодом T. Ведь значение производной в точке x равно тангенсу угла наклона касательной графика ее первообразной в этой точке к оси абсцисс, а поскольку первообразная периодически повторяется, то должна повторяться и производная. Например, производная от функции sin(x) равна cos(x), и она периодична. Беря производную от cos(x), вы получите –sin(x). Периодичность сохраняется неизменно.

Однако обратное не всегда верно. Так, функция f(x) = const периодическая, а ее первообразная F(x) = const*x + C — нет.

Если F1(x) и F2(x) — периодические функции, и их периоды равны T1 и T2 соответственно, то сумма этих функций тоже может быть периодической. Однако ее период не будет простой суммой периодов T1 и T2. Если результат деления T1/T2 — рациональное число, то сумма функций периодична, и ее период равен наименьшему общему кратному (НОК) периодов T1 и T2. Например, если период первой функции равен 12, а период второй — 15, то период их суммы будет равен НОК (12, 15) = 60.

Наглядно это можно представить так: функции идут с разной «шириной шага», но если отношение их ширин рационально, то рано или поздно (а точнее, именно через НОК шагов), они снова сравняются, и их сумма начнет новый период.

Источник

Периодические функции

С периодическими функциями мы встречаемся в школьном курсе алгебры. Это функции, все значения которых повторяются через определенный период. Как будто мы копируем часть графика — и повторяем этот паттерн на всей области определения функции. Например, — периодические функции.

Дадим определение периодической функции:

Например, — периодические функции.

Для функций и период

Но не только тригонометрические функции являются периодическими. Если вы учитесь в матклассе или на первом курсе вуза — вам могут встретиться вот такие задачи:

1. Периодическая функция определена для всех действительных чисел. Ее период равен двум и Найдите значение выражения

График функции может выглядеть, например, вот так:

Как ведет себя функция в других точках — мы не знаем. Но знаем, что ее график состоит из повторяющихся элементов длиной 2, что и нарисовано.

2. График четной периодической функции совпадает с графиком функции на отрезке от 0 до 1; период функции равен 2. Постройте график функции и найдите f(4 ).

Построим график функции при

Поскольку функция четная, ее график симметричен относительно оси ординат. Построим часть графика при симметричную части графика от 0 до 1.

Период функции равен 2. Повторим периодически участок длины 2, который уже построен.

3. Найдите наименьший положительный период функции

Наименьший положительный период функции равен

График функции получается из графика функции сжатием в 3 раза по оси X (смотри тему «Преобразование графиков функций).

Рассуждая аналогично, получим, что для функции наименьший положительный период равен На отрезке укладывается ровно 5 полных волн функции

4. Период функции равен 12, а период функции равен 8. Найдите наименьший положительный период функции

Наименьший положительный период суммы функций равен наименьшему общему кратному периодов слагаемых.

Источник

§ 13. Свойства тригонометрических функций

Объяснение и обоснование

ления этих функций.

Например, — это ордината соответствующей точки единичной

окружности. Поэтому значение будет положительным, если точка

имеет положительную ординату, a это будет тогда, когда точка находит-

верти, то ее ордината отрицательна, и поэтому тоже отрицателен.

Аналогично, учитывая, что — это абсцисса соответствующей точки ,

получаем, что >0 в I и IV четвертях (абсцисса точки положительна)

и Функция y = f (x) называется периодической с периодом T ≠ 0, если для

любого x из области определения функции числа (x + T) и (x – T) также

Из приведенного определения получаем, что f (x – T) = f ((x – T) + T) =

= f (x), то есть, если T — период функции f (x), то и – T тоже период этой

Учитывая, что на единичной окружности числам (углам) где

соответствует одна и та же точка (рис. 71), получаем:

Тогда является периодом функций и .

При k = 1 получаем, что — это период функций и .

Докажем, что эти функции не могут иметь меньший положительный пе-

риод. Чтобы доказать, что — наименьший положительный период

бого значения x выполняется равенство cos (x + T) = cos x. Взяв x = 0,

получаем cos T = 1. Но это означает, что на единичной окружности при

повороте на угол T точка снова попадает в точку , то есть ,

где k ∈ Z. Таким образом, любой период косинуса должен быть кратным

, а значит,

— наименьший положительный период косинуса.

Чтобы обосновать, что — наименьший положительный период

функции sin x, достаточно в равенстве sin (x + T) = sin x, которое выпол-

няется для любых значений x, взять . Получаем Но это

означает, что при повороте на угол точка попадает в точку A (0;1)

(рис. 71), то есть таким образом . Следовательно,

любой период синуса должен быть кратным , а значитит,

— наименьший положительный период косинуса.

Если учесть, что на единичной окружности точки и являются

диаметрально противоположными, то этим точкам соответствует одна и та же

точка на линии тангенсов (рис. 72) или на линии котангенсов (рис. 73). Тогда

также

То есть периодом функций tg x и ctg x является (k ≠ 0, k ∈ Z).

Наименьшим положительным периодом для функций tg x и ctg x явля-

ется

Чтобы доказать это, достаточно в равенстве tg (x + T) = tg x взять x = 0.

Тогда получим tg T = 0. Таким образом, T =, где k ∈ Z. Итак, любой

период тангенса должен быть кратным а значит, — наименьший по-

ложительный период тангенса. Аналогично в соответствующем равенстве

для ctg x достаточно взять .

ции y = f (x), напомним, что по определению график функции y = f (x)

ординаты (x; y) = (x; f (x)). Первая координата для точек графика вы-

бирается произвольно из области определения функции. Выберем как

первую координату значение x + T (или в обобщенном виде — значение

x + kT при целом значении k) и учтем, что для периодической функции

f(x + T) = f(x – T) = f (x) (в общем случае f (x + kT) = f (x)). Тогда графи-

ку функции y = f (x) будет принадлежать также точка M1 координатной

плоскости с координатами:

(x + T; y) = (x + T; f (x + T)) = (x + T; f (x)).

ным переносом вдоль оси Ox на T единиц (рис. 74). В общем случае точку

реносом вдоль оси Ox на kT единиц. Таким образом, через промежуток T

вид графика периодической функции будет повторяться. Поэтому для

построения графика периодической функции с периодом T достаточно

построить график на любом промежутке длиной T(например, на проме-

жутке [0;T]), а потом полученную линию параллельно перенести вправо

и влево вдоль оси Ox на расстояние kT, где k — любое натуральное число.

Примеры решения задач

Задача 1 Пользуясь периодичностью, четностью и нечетностью триго-

нометрических функций, найдите:

Задача 1 Докажите утверждение: если функция y = f (x) периодическая

с периодом T, то функция y = Af (kx + b) также периодическая

с периодом (A, k, b — некоторые числа и k ≠ 0).

Используем утверждение, доказанное в задаче 2 для нахождения перио-

1) если функция sin x имеет период , то функция sin 4x имеет период

2) если функция tg x имеет период ,то функция имеет период

Вопросы для контроля

б *) Обоснуйте знаки тригонометрических функций в каждой из коорди-

2. а) Какие из тригонометрических функций являются четными, а какие

нечетными? Приведите примеры использования четности и нечетности

для вычисления значений тригонометрических функций.

б *) Обоснуйте четность или нечетность соответствующих тригонометри-

3. а) Какая функция называется периодической? Приведите примеры.

б *) Обоснуйте периодичность тригонометрических функций. Укажи-

те наименьший положительный период для синуса, косинуса, тангенса

и котангенса и обоснуйте, что в каждом случае этот период действитель-

но является наименьшим положительным периодом.

Упражнения

1. Пользуясь периодичностью, четностью и нечетностью тригонометриче-

ской функции, найдите:

1) 2) sin (–750°); 3) 4) ctg 945°;

5) 6) cos (–3630°); 7) 8) tg 600°.

2*. Среди данных функций найдите периодические и укажите наименьший

положительный период для каждой из них:

1) f(x)= x^2; 2) f(x)= sin 2x; 3) f(x)= | x |; 4) f(x)= tg 3x; 5)f(x) = 3.

3. Найдите период каждой из данных функций:

1) y= cos 2x; 2)y = tg 5x; 3) 4) y = ctg 3x; 5)

4. На каждом из рисунков 75–78 приведена часть графика некоторой перио-

дической функции с периодом T. Продолжите график на отрезке [–2T; 3T].

Источник