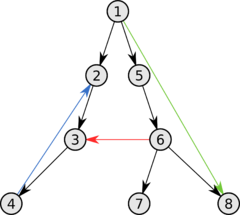
Что такое глубина поиска
Алгоритм DFS («Depth-first search» или «Поиск в глубину»)
Алгоритм DFS
Стандартная реализация DFS помещает каждую вершину графа в одну из двух категорий:
Алгоритм DFS работает следующим образом:
Пример DFS
Давайте посмотрим, как алгоритм «поиска в глубину» работает на примере. Мы используем неориентированный граф с 5 вершинами.
Мы начинаем с вершины 0, алгоритм DFS начинается с помещения его в список посещенных и размещения всех смежных вершин в стеке.
Затем мы посещаем элемент в верхней части стека, то есть 1, и переходим к смежным узлам. Так как 0 мы уже посетили, вместо этого посещаем 2.
У вершины 2 есть не посещенная смежная вершина 4, поэтому мы добавляем ее в верхнюю часть стека и посещаем.
После того, как мы посетим последний элемент 3, у него нет не посещенных смежных узлов. На этом мы завершим первый «обход в глубину» графа.
Псевдокод DFS (рекурсивная реализация)
Псевдокод для DFS показан ниже. Обратите внимание, что в функции init() мы запускаем функцию DFS на каждом узле. Это связано с тем, что граф может иметь две разные несвязанные части, поэтому, чтобы убедиться, что мы покрываем каждую вершину, мы также можем запустить алгоритм DFS на каждом узле.
Код DFS
Код для алгоритма «поиска в глубину» с примером показан ниже. Код был упрощен, поэтому мы можем сосредоточиться на алгоритме, а не на других деталях.
Поиск в глубину.
Поиск в глубину (англ. depth-first search, DFS) – это рекурсивный алгоритм обхода вершин графа. Если метод поиска в ширину производился симметрично (вершины графа просматривались по уровням), то данный метод предполагает продвижение вглубь до тех пор, пока это возможно. Невозможность дальнейшего продвижения, означает, что следующим шагом будет переход на последний, имеющий несколько вариантов движения (один из которых исследован полностью), ранее посещенный узел (вершина).
Отсутствие последнего свидетельствует об одной из двух возможных ситуаций: либо все вершины графа уже просмотрены, либо просмотрены все те, что доступны из вершины, взятой в качестве начальной, но не все (несвязные и ориентированные графы допускают последний вариант).
Рассмотрим то, как будет вести себя алгоритм на конкретном примере. Приведенный далее неориентированный связный граф имеет в сумме 5 вершин. 
Пусть обход начнется с узла 1, тогда порядок последовательности просмотренных узлов будет следующим: 1 2 3 5 4. Если выполнение начать, например, с узла 3, то порядок обхода окажется иным: 3 2 1 5 4.
Алгоритм поиска в глубину базируется на рекурсии, т. е. функция обхода, по мере выполнения, вызывает сама себя, что делает код в целом довольно компактным.
Псевдокод алгоритма:
Здесь DFS (depth-firstsearch) – название функции. Единственный ее параметр st – стартовый узел, передаваемый из главной части программы как аргумент. Каждому из элементов логического массива visited заранее присваивается значение false, т. е. каждая из вершин изначально будет значиться как не посещенная.
Двумерный массив graph – это матрица смежности графа. Большую часть внимания следует сконцентрировать на последней строке. Если элемент матрицы смежности, на каком то шаге равен 1 (а не 0) и вершина с тем же номером, что и проверяемый столбец матрицы при этом не была посещена, то функция рекурсивно повторяется. В противном случае функция возвращается на предыдущую стадию рекурсии.
Обход в глубину, цвета вершин
Обход в глубину (поиск в глубину, англ. Depth-First Search, DFS) — один из основных методов обхода графа, часто используемый для проверки связности, поиска цикла и компонент сильной связности и для топологической сортировки.
Содержание
Алгоритм [ править ]
Общая идея [ править ]
Общая идея алгоритма состоит в следующем: для каждой не пройденной вершины необходимо найти все не пройденные смежные вершины и повторить поиск для них.
Пошаговое представление [ править ]
Реализация [ править ]
В массиве [math]\mathrm
Время работы [ править ]
Цвета вершин [ править ]
Зачастую, простой информации «были/не были в вершине» не хватает для конкретных целей.
Поэтому в процессе алгоритма вершинам задают некоторые цвета:
Такие «метки» в основном используются при поиске цикла.
Реализация [ править ]
Пример [ править ]
Рассмотрим, как будут изменяться цвета вершин при обходе в глубину данного графа.
Дерево обхода в глубину [ править ]
Алгоритм [math]\mathrm
Алгоритмы на графах — Часть 1: Поиск в глубину и проблема взаимоблокировок
Недавно на Хабре была статья, посвященная алгоритмам на графах. С позволения автора, мой первый хабратопик продолжит цикл.
Хотелось бы осветить вопросы применения некоторых алгоритмов, для решения задач программирования.
Достаточно жизненный пример, с которым сталкивался не один разработчик — это deadlock. По сути deadlock – это взаимоблокировка, в результате которой система, или какие-то отдельные процессы начинают конкурировать за один ресурс.
В жизни такие ситуации встречаются, например, когда два человека желают пропустить друг друга на входе, предположим, в аудиторию. Однако после 3-4 фраз «только после вас!», кто-нибудь всё же пройдет первым.
На уровне программного обеспечения всё сложнее, пока программы не способны думать, машинный аналог фразы «только после вас!» будет повторяться вплоть до перезагрузки.
Как исполняющая система может повлиять на этот процесс? Вот тут нам на помощь и приходят алгоритмы на графах.
Для начала определимся, что же будет элементами нашего графа, и как его составить.
Возьмем более «машинный» пример: однопоточное java приложение с выходом в интернет. Представим, что наш код и система вывода сообщений будут выполняться в одном потоке, в этом случае, перед открытием соединения буден инициирован запрос пользователю, действительно ли он доверяет этому приложению пользоваться интернетом. Возникает блокировка, код не завершится, пока пользователь не нажмет «OK», но вывод сообщений будет возможен только после завершения кода. Попробуем построить граф для этого примера.
Вершинами обозначим функциональные узлы программы, дугами – внешние запросы, необходимые для продолжения работы узла.
Определим контур, как путь из какой либо вершины в саму себя. В таком случае на нашем графе каждый контур будет иллюстрировать возникший deadlock.
Теперь все готово для формального описания самого алгоритма.
1. Пронумеруем все вершины графа
2. Отметить все вершины графа, как новые
3. Отметить все дуги графа, как новые
4. Поместим произвольную вершину графа в стек
5. Пока стек не пуст, прочитать (не выталкивая) из стека последнюю вершину и применить к ней процедуру Find(Node V)
6. Если стек пуст, но остались новые вершины, положить в стек любую из новых и перейти к п.5
Где D.LinkNode — вершина, на которую указывает дуга.
Пример реализации алгоритма:
Для начала нам понадобится объявить тип данных для графа и его вершин
public class GraphNode
<
public bool New;
public List Links;
>
Теперь реализуем класс, выполняющий поиск контуров
public static class PathFinder
<
static List list;
static List List > paths;
public static List List > Find(Graph graph)
static void InternalFind(GraphNode node)
>
И, собственно, наши основные функции:
static List List > Find(Graph graph)
<
list = new List (); //Имитируем стек
paths = new List List >(); //Результирующий список контуров
foreach (GraphNode node in graph.Nodes)
<
node.New = true ;
>
list.Add(graph.Nodes[0]); //Добавляем первую вершину для начала алгоритма
// Поиск оставшихся новых вершин
done = true ;
foreach (GraphNode node in graph.Nodes)
<
if (node.New)
<
list.Add(node);
done = false ;
break ;
>
>
>
return paths;
>
Стек был намеренно реализован списком, т.к. нам надо будет считывать из него найденные контура, не выталкивая элементы
static void InternalFind(GraphNode node)
<
node.New = false ;
foreach (GraphNode nextNode in node.Links) //Итерация по всем дугам текущей вершины
<
if (nextNode.New)
<
list.Add(nextNode);
InternalFind(nextNode);
>
for ( int i = firstElement; i
Графически, алгоритм можно рассмотреть так:
Из вершины «0», которая является началом пути, мы движемся вниз, если на очередном шаге алгоритм находит дугу, указывающую на вершину, находящуюся в стеке (в данном случае дуга исходит из вершины «4»), из вершин стека образуется контур (на примере: 0-2-3-4-5-0), соответственно, если дуга указывает на уже не новую вершину, но уже вытолкнутую из стека (например на вершину «1»), контура не возникает.
Данный алгоритм известен как поиск в глубину в ориентированном графе.
Таким образом, исполняющей среде остаётся только отслеживать все вызовы методов и, периодически, проверять наличие блокировок.
Как бороться с найденными блокировками? Иногда deadlock бывает настолько запутанным, что гораздо проще перезапустить взаимоблокируемый код, в любом случае, это уже должно решаться индивидуально для конкретной системы.
В следующий раз (с моей стороны) – алгоритм топологической сортировки, который, в том числе, может быть применен при компиляции и анализе цепи активаций нейронов в нейросети.
UPD: Добавил пример кода
UPD2: Перенес в алгоритмы, спасибо
Обход графа: поиск в глубину и поиск в ширину простыми словами на примере JavaScript
Доброго времени суток.
Что такое обход графа?
Простыми словами, обход графа — это переход от одной его вершины к другой в поисках свойств связей этих вершин. Связи (линии, соединяющие вершины) называются направлениями, путями, гранями или ребрами графа. Вершины графа также именуются узлами.
Двумя основными алгоритмами обхода графа являются поиск в глубину (Depth-First Search, DFS) и поиск в ширину (Breadth-First Search, BFS).
Несмотря на то, что оба алгоритма используются для обхода графа, они имеют некоторые отличия. Начнем с DFS.
Поиск в глубину
DFS следует концепции «погружайся глубже, головой вперед» («go deep, head first»). Идея заключается в том, что мы двигаемся от начальной вершины (точки, места) в определенном направлении (по определенному пути) до тех пор, пока не достигнем конца пути или пункта назначения (искомой вершины). Если мы достигли конца пути, но он не является пунктом назначения, то мы возвращаемся назад (к точке разветвления или расхождения путей) и идем по другому маршруту.
Давайте рассмотрим пример. Предположим, что у нас есть ориентированный граф, который выглядит так:
Мы находимся в точке «s» и нам нужно найти вершину «t». Применяя DFS, мы исследуем один из возможных путей, двигаемся по нему до конца и, если не обнаружили t, возвращаемся и исследуем другой путь. Вот как выглядит процесс:
Здесь мы двигаемся по пути (p1) к ближайшей вершине и видим, что это не конец пути. Поэтому мы переходим к следующей вершине.
Мы достигли конца p1, но не нашли t, поэтому возвращаемся в s и двигаемся по второму пути.
Достигнув ближайшей к точке «s» вершины пути «p2» мы видим три возможных направления для дальнейшего движения. Поскольку вершину, венчающую первое направление, мы уже посещали, то двигаемся по второму.
Мы вновь достигли конца пути, но не нашли t, поэтому возвращаемся назад. Следуем по третьему пути и, наконец, достигаем искомой вершины «t».
Так работает DFS. Двигаемся по определенному пути до конца. Если конец пути — это искомая вершина, мы закончили. Если нет, возвращаемся назад и двигаемся по другому пути до тех пор, пока не исследуем все варианты.
Мы следуем этому алгоритму применительно к каждой посещенной вершине.
Необходимость многократного повторения процедуры указывает на необходимость использования рекурсии для реализации алгоритма.
Заметка: этот специальный DFS-алгоритм позволяет проверить, возможно ли добраться из одного места в другое. DFS может использоваться в разных целях. От этих целей зависит то, как будет выглядеть сам алгоритм. Тем не менее, общая концепция выглядит именно так.
Анализ DFS
Давайте проанализируем этот алгоритм. Поскольку мы обходим каждого «соседа» каждого узла, игнорируя тех, которых посещали ранее, мы имеем время выполнения, равное O(V + E).
Краткое объяснение того, что означает V+E:
V — общее количество вершин. E — общее количество граней (ребер).
Может показаться, что правильнее использовать V*E, однако давайте подумаем, что означает V*E.
V*E означает, что применительно к каждой вершине, мы должны исследовать все грани графа безотносительно принадлежности этих граней конкретной вершине.
С другой стороны, V+E означает, что для каждой вершины мы оцениваем лишь примыкающие к ней грани. Возвращаясь к примеру, каждая вершина имеет определенное количество граней и, в худшем случае, мы обойдем все вершины (O(V)) и исследуем все грани (O(E)). Мы имеем V вершин и E граней, поэтому получаем V+E.
Далее, поскольку мы используем рекурсию для обхода каждой вершины, это означает, что используется стек (бесконечная рекурсия приводит к ошибке переполнения стека). Поэтому пространственная сложность составляет O(V).
Теперь рассмотрим BFS.
Поиск в ширину
BFS следует концепции «расширяйся, поднимаясь на высоту птичьего полета» («go wide, bird’s eye-view»). Вместо того, чтобы двигаться по определенному пути до конца, BFS предполагает движение вперед по одному соседу за раз. Это означает следующее:
Вместо следования по пути, BFS подразумевает посещение ближайших к s соседей за одно действие (шаг), затем посещение соседей соседей и так до тех пор, пока не будет обнаружено t.
Чем DFS отличается от BFS? Мне нравится думать, что DFS идет напролом, а BFS не торопится, а изучает все в пределах одного шага.
Далее возникает вопрос: как узнать, каких соседей следует посетить первыми?
Для этого мы можем воспользоваться концепцией «первым вошел, первым вышел» (first-in-first-out, FIFO) из очереди (queue). Мы помещаем в очередь сначала ближайшую к нам вершину, затем ее непосещенных соседей, и продолжаем этот процесс, пока очередь не опустеет или пока мы не найдем искомую вершину.
Анализ BFS
Может показаться, что BFS работает медленнее. Однако если внимательно присмотреться к визуализациям, можно увидеть, что они имеют одинаковое время выполнения.
Очередь предполагает обработку каждой вершины перед достижением пункта назначения. Это означает, что, в худшем случае, BFS исследует все вершины и грани.
Несмотря на то, что BFS может казаться медленнее, на самом деле он быстрее, поскольку при работе с большими графами обнаруживается, что DFS тратит много времени на следование по путям, которые в конечном счете оказываются ложными. BFS часто используется для нахождения кратчайшего пути между двумя вершинами.
Таким образом, время выполнения BFS также составляет O(V + E), а поскольку мы используем очередь, вмещающую все вершины, его пространственная сложность составляет O(V).
Аналогии из реальной жизни
Если приводить аналогии из реальной жизни, то вот как я представляю себе работу DFS и BFS.
Когда я думаю о DFS, то представляю себе мышь в лабиринте в поисках еды. Для того, чтобы попасть к цели мышь вынуждена много раз упираться в тупик, возвращаться и двигаться по другому пути, и так до тех пор, пока она не найдет выход из лабиринта или еду.
Упрощенная версия выглядит так:
В свою очередь, когда я думаю о BFS, то представляю себе круги на воде. Падение камня в воду приводит к распространению возмущения (кругов) во всех направлениях от центра.
Упрощенная версия выглядит так: