Что такое гомоморфизм колец
Теория колец
Множества с двумя алгебраическими операциями. Кольца и поля.
Пусть на множестве R определены две алгебраические операции, которые мы будем называть сложением и умножением и обозначать соответственно + и *. Говорят, что умножение обладает свойством (правой) дистрибутивности относительно сложения, если
. (1)
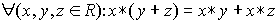
Полем называется такое ассоциативное коммутативное кольцо с единицей k, в котором всякий ненулевой элемент обратим: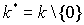 
.
Таким образом, по определению в поле отсутствуют делители нуля.
Примеры колец и полей.
Ядро гомоморфизма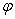 
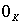
— это ядро группового гомоморфизма аддитивных групп 
, то есть множество всех элементов из R, которые отображаются в 
.
Подкольцо К называется идеалом кольца R, если 
: x*K 
K и K*yK.
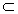
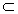
Мы видим, что если К является идеалом в R, произведение смежных классов (r+K)*(s+K) содержится в смежном классе r*s+K. Значит в факторгруппе R/K определена операция умножения, превращающая ее в кольцо, называемое факторкольцом кольца R по идеалу К.
Свойства ассоциативности, коммутативности и наличия единицы очевидно сохраняются при переходе к факторкольцу. Напротив, отсутствие в R делителей нуля еще не гарантирует их отсутствие в факторкольце (см. пример 1).
Ядро гомоморфизма колец является идеалом.
Пусть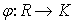 
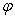
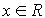
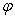
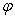
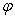
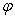
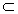
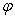
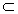
— гомоморфизм колец, I =Ker
, 
— любой элемент. Тогда, (x*I) =(x)*(I) =(x)*0 =0. Значит, x*IKer =I. Аналогично проверяется, что I*xI.
Пусть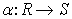 
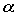
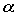
— сюръективный гомоморфизм колец. Тогда S изоморфно факторкольцу R/Ker
. Если эти изоморфные кольца отождествить, то отождествляется с естественным гомоморфизмом кольца R на свое факторкольцо.
Доказательство этой теоремы аналогично доказательству соответствующей теоремы для групп и мы его опускаем.
Кольцо многочленов над полем.
Общим наибольшим делителем ненулевых многочленов p и s называется такой унитарный многочлен ОНД( p, s), что
По определению, для ненулевого многочлена р со старшим коэффициентом а ОНД (р, 0) = ОНД (0, р) = р/а; ОНД (0, 0)=0.
Аналогично определяется ОНД любого числа многочленов.
Единственность ОНД двух многочленов непосредственно вытекает из определения. Существование его следует из следующего утверждения.
Основная теорема теории делимости ( для многочленов).
Для любых двух ненулевых многочленов p и q над полем k можно найти такие многочлены u и v над тем же полем, что ОНД(p, q)= u*p+v*q.
II. Разложение на множители.
Свойства неприводимых многочленов.
В самом деле, p = d*s и если deg(s )>0, то это противоречит неприводимости p, а если deg(s )=0, то d | q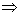
p | q.
2. Если p |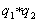 
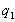
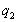
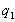
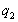
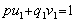
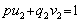
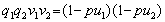
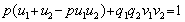
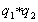
и p неприводим, то либо p | 
либо p | 
. Действительно, в противном случае НОД(p, ) = НОД(p, 
) =1 и потому по основной теореме теории делимости 
; 
, откуда: 
и значит, 
, то есть НОД(p, 
)=1 и, следовательно, deg (p )=0.
III. Корни многочленов. Производная и кратные корни.
Ошибка в тексте? Выдели её мышкой и нажми 
гомоморфизм колец
Смотреть что такое «гомоморфизм колец» в других словарях:
Гомоморфизм — Не следует путать с гомеоморфизмом. Гомоморфизм (от др. греч. ὁμός равный, одинаковый и μορφή вид, форма) это морфизм в категории алгебраических систем. Это отображение алгебраической системы А, сохраняющее основные операции и… … Википедия
МОДУЛЬ — абелева группа с кольцом операторов. М. является обобщением (линейного) векторного пространства над полем Кдля случая, когда Кзаменяется нек рым кольцом. Пусть задано кольцо А. Аддитивная абелева группа Мназ. левым А модулем, если определено… … Математическая энциклопедия
Идеал (алгебра) — У этого термина существуют и другие значения, см. Идеал (значения). Идеал одно из основных понятий абстрактной алгебры. Наибольшее значение идеалы имеют в теории колец, но также определяются и для полугрупп, алгебр и некоторых других… … Википедия
КЛАССОВ ДИВИЗОРОВ ГРУППА — факторгруппа группы диеизориалъных идеалов D (А) Крулля кольца А по подгруппе главных идеалов F(A). К. д. г. является абелевой группой и обычно обозначается С(А). Группа С(А)порождается классами простых идеалов высоты 1 в кольце А. В некотором… … Математическая энциклопедия
Ядро линейного отображения — В различных разделах математики ядром отображения называется некоторое множество kerf, в некотором смысле характеризующее отличие f от инъективного отображения. Конкретное определение может различаться, однако для инъективного отображения f… … Википедия
Теоремы об изоморфизме — Запрос «Теорема об изоморфизме» перенаправляется сюда; см. также другие значения. Первая теорема об изоморфизме Т … Википедия
ТОПОЛОГИЧЕСКОЕ КОЛЬЦО — кольцо R, являющееся топологич. пространством, причем требуется, чтобы отображения были непрерывны. Т. к. Rназ. отделимым, если оно отделимо как топологич. пространство. В этом случае пространство R хаусдорфово. Любое подкольцо МТ. к. R, а также… … Математическая энциклопедия
АФФИННАЯ СХЕМА — обобщение понятия аффинного многообразия, играющее роль локального объекта в теории схем. Пусть А коммутативное кольцо с единицей. Аффинная схема состоит из топо логич. пространства Spec Аи пучка колец на Spec A. При этом Spec Аесть множество… … Математическая энциклопедия
Кольцо (математика) — У этого термина существуют и другие значения, см. Кольцо. В абстрактной алгебре кольцо это один из наиболее часто встречающихся видов алгебраической структуры. Простейшими примерами колец являются алгебры чисел (целых, вещественных,… … Википедия
Инструменты пользователя
Инструменты сайта
Содержание
Кольцо (математика)
Кольца являются основным объектом изучения теории колец — крупного раздела общей алгебры, в котором разработаны инструментальные средства, нашедшие широкое применение в алгебраической геометрии, алгебраической теории чисел, алгебраической
История
Определение
Кольца могут обладать следующими дополнительными свойствами:
Простейшие свойства
Непосредственно из аксиом кольца можно вывести следующие свойства:
Основные понятия
Виды элементов кольца
Пусть в кольце есть элементы, отличные от нуля (кольцо не является тривиальным). Тогда левый делитель нуля — это ненулевой элемент кольца для которого существует ненулевой элемент кольца такой что Аналогично определяется правый делитель нуля. В коммутативных кольцах эти понятия совпадают. Пример: рассмотрим кольцо непрерывных функций на интервале Положим тогда то есть являются делителями нуля. Здесь условие означает, что является функцией, отличной от нуля, но не означает, что нигде не принимает значение 8)
Идемпотентный элемент — это такой элемент, что Например, идемпотентен любой оператор проектирования, в частности, следующий: в кольце матриц 10)
Если – произвольный элемент кольца с единицей то левым обратным элементом к называется такой, что Правый обратный элемент определяется аналогично. Если у элемента есть как левый, так и правый обратный элемент, то последние совпадают, и говорят, что обладает обратным элементом, который определён однозначно и обозначается Сам элемент называется обратимым элементом. 11)
Подкольцо
Подмножество называется подкольцом если само является кольцом относительно операций, определенных в При этом говорят, что – расширение кольца 12) Другими словами, непустое подмножество является подкольцом, если
По определению, подкольцо непусто, поскольку содержит нулевой элемент. Нуль и единица кольца являются нулем и единицей любого его подкольца. 13)
Подкольцо наследует свойство коммутативности. 14)
Пересечение любого множества подколец является подкольцом. Наименьшее подкольцо, содержащее подмножество называется подкольцом, порождённым а — системой образующих для кольца Такое подкольцо всегда существует, так как пересечение всех подколец, содержащих удовлетворяет этому определению. 15)
Подкольцо кольца с единицей порождённое его единицей, называется наименьшим или главным подкольцом кольца Такое подкольцо содержится в любом подкольце кольца 16)
Идеалы
Непустое подмножество кольца называется левым идеалом, если:
Из первого свойства следует и замкнутость I относительно умножения внутри себя, так что I является подкольцом.
Аналогично определяется правый идеал, замкнутый относительно умножения на элемент кольца справа.
Двусторонний идеал (или просто идеал) кольца — любое непустое подмножество, являющееся одновременно левым, так и правым идеалом.
Также идеал кольца может определяться как ядро некоторого гомоморфизма 18)
Идеал кольца, не совпадающий со всем кольцом, называется простым, если факторкольцо по этому идеалу не имеет делителей нуля.
Идеал кольца, не совпадающий со всем кольцом и не содержащийся ни в каком большем идеале, не равном кольцу, называется максимальным. 20)
Гомоморфизм
Гомоморфизм колец (кольцевой гомоморфизм) — это отображение, сохраняющее операции сложения и умножения. А именно, гомоморфизм из кольца в кольцо — это функция такая что
Гомоморфизм колец называется изоморфизмом, если существует обратный гомоморфизм колец. Любой биективный гомоморфизм колец является изоморфизмом. Автоморфизм — это гомоморфизм из кольца в себя, который является изоморфизмом. Пример: тождественное отображение кольца на себя является автоморфизмом. 23)
Факторкольцо
Определение факторкольца по идеалу аналогично определению факторгруппы. Более точно, факторкольцо кольца по двустороннему идеалу — это множество классов смежности аддитивной группы по аддитивной подгруппе со следующими операциями:
Аналогично случаю групп, существует канонический гомоморфизм задаваемый как Ядром при этом является идеал
Аналогично теореме о гомоморфизме групп существует теорема о гомоморфизме колец: пусть тогда изоморфен факторкольцу по ядру гомоморфизма 26)
Некоторые особые классы колец
Примеры
Конструкции
Прямое произведение
Сходная конструкция существует для произведения произвольного семейства колец (сложение и умножение задаются покомпонентно). 43)
Пусть — коммутативное кольцо и — попарно взаимно простые идеалы в нём (идеалы называются взаимно простыми, если их сумма равна всему кольцу). Китайская теорема об остатках утверждает, что отображение
Кольцо эндоморфизмов
Поле частных и кольцо частных
Пусть R — целостное кольцо, тогда следующая конструкция позволяет построить наименьшее поле, содержащее его. Поле частных кольца R — это множество классов эквивалентности формальных дробей по следующему отношению эквивалентности:
тогда и только тогда, когда
с обычными операциями:
Не вполне очевидно, что заданное отношение действительно является отношением эквивалентности: для доказательства приходиться воспользоваться целостностью кольца. Существует обобщение данной конструкции на произвольные коммутативные кольца. А именно, пусть S — мультипликативно замкнутая система в коммутативном кольце R (то есть подмножество, содержащее единицу и не содержащее нуля; произведение любых двух элементов из подмножества снова ему принадлежит). Тогда кольцо частных — это множество классов эквивалентности формальных дробей по отношению эквивалентности:
Также эту конструкцию называют локализацией кольца (так как в алгебраической геометрии она позволяет исследовать локальные свойства многообразия в отдельной его точке). Пример: кольцо десятичных дробей — это локализация кольца целых чисел по мультипликативной системе
Категорное описание
Кольца вместе с гомоморфизмами колец образуют категорию, обычно обозначаемую Ring (иногда так обозначают категорию колец с единицей, а категорию обычных колец обозначают Rng). Категория колец с единицей обладает многими полезными свойствами: в частности, она полна и кополна. Это значит, что в ней существуют все малые пределы и копределы (например, произведения, копроизведения, ядра и коядра). Категория колец с единицей обладает начальным объектом (кольцо ) и терминальным объектом (нулевое кольцо).
Можно дать следующее категорное определение кольца: ассоциативное кольцо с единицей — это моноид в категории абелевых групп (абелевы группы образуют моноидальную категорию относительно операции тензорного произведения). Действие кольца R на абелевой группе (кольца, рассматриваемого как моноид по умножению) превращает абелеву группу в R-модуль. Понятие модуля обобщает понятие векторного пространства: грубо говоря, модуль — это «векторное пространство над кольцом». 48) 49)