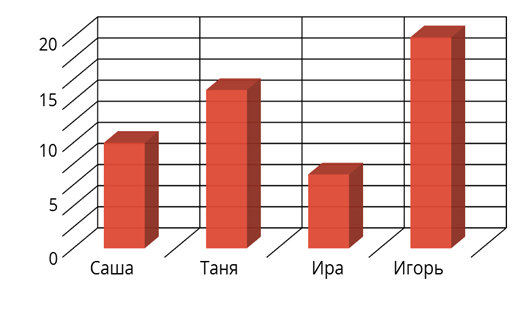Что такое графическая модель ситуации
Графические информационные модели. Многообразие графических информационных моделей
Урок 5. Информатика 9 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Графические информационные модели. Многообразие графических информационных моделей»
Графическая информационная модель – это наглядный способ представления объектов и процессов в виде графических изображений. Графические информационные модели являются простейшим видом моделей. С их помощью передаются внешние признаки объекта – размер, форма, цвет. Графические модели несут в себе больше информации, чем словесные.
Для более наглядного и понятного представления информации в графических информационных моделях используются графические изображения (образные элементы), которые могут быть дополнены текстами, числами и символами. Примерами графических информационных моделей являются схемы, карты, чертежи, графики, диаграммы и много другое.
Разберёмся более подробно с каждой из них.
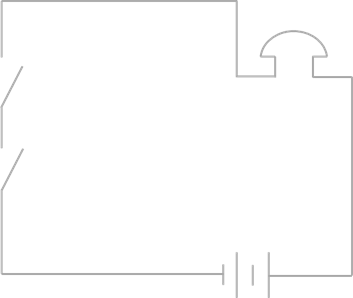
Cхема – это графическое отображение состава и структуры сложной системы. Можно обратиться к ранее рассматриваемому примеру: две электрические схемы соединения переключателей.
Схема последовательного соединения переключателей
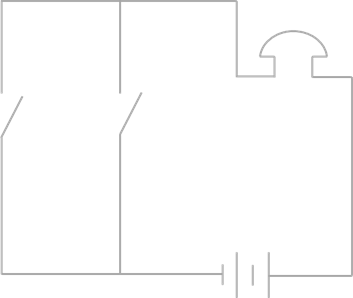
Схема параллельного соединения переключателей
На первой представлено последовательное соединение, а на второй – параллельное. Можно заметить, что с помощью схемы легче разбираться с такими задачами, нежели использовать словесное описание. Схемы используются на уроках биологии, истории и так далее.
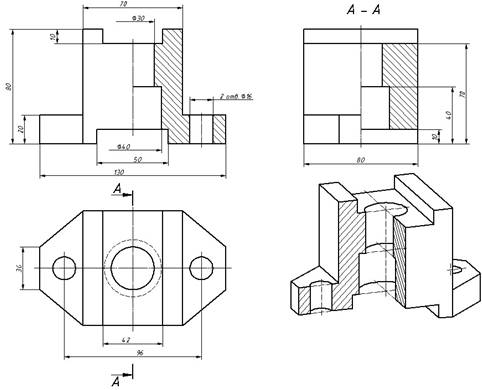
Следующая графическая информационная модель – чертеж. Чертеж – это условное графическое изображение предмета с точным соотношением его размеров, получаемое методом моделирования. При построении чертежа используются изображения, числа, текст. С помощью изображений мы получаем представление о форме объекта, с помощью чисел – о размере, с помощью текста – о названии объектов, размерах, в которых выполнены изображения. Примером чертежа является изображение детали перед её изготовлением.
На чертеже изображена деталь в разрезе, чтобы лучше было видно все части, составляющие нашу деталь, присутствуют размеры (числа).
Рассмотрим такую графическую информационную модель как карта. Карта используется для отображения местности в уменьшенном масштабе, которая является для нее объектом моделирования. Например, с помощью карты мы можем узнать сколько километров от Москвы до Санкт-Петербурга, как добраться на метро или автобусе с одного остановочного пункта до другого, где находится Будапешт и много другое. Для различных целей используются разнообразные карты: политическая, географическая, тематическая и другие.
Перейдем к графикам. График – это графическое изображение, которое отображает зависимость одной величины от другой, динамику какого-либо процесса в течение какого-либо периода и много другое.
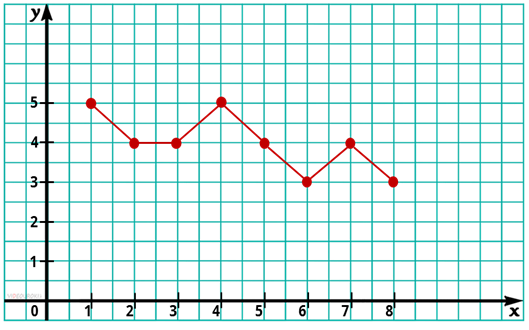
Расставим точки в соответствии с данными на координатной плоскости и соединим их линиями.
Мы получили необходимый график, с помощью которого можно сделать вывод, что знания Максима по математике ухудшились. Ещё одним примером графика является кардиограмма сердца. Кардиограмма точно определяет в каком ритме бьётся сердце.
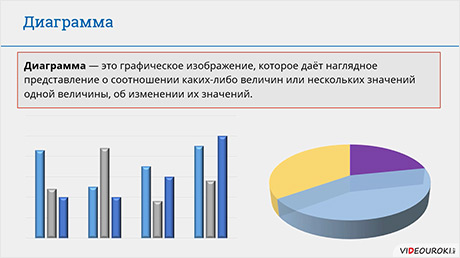
Перейдём к диаграммам. Диаграмма – это графическое изображение, которое даёт наглядное представление о соотношении каких-либо величин или нескольких значений одной величины, об изменении их значений. Диаграммы бывают нескольких видов, но более подробно мы с ними познакомимся при изучении электронных таблиц.
А сейчас рассмотрим несколько примеров.
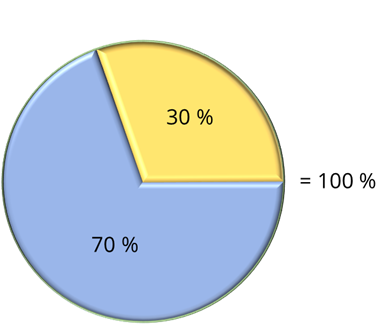
Первый: Наша планета состоит из воды и суши. Вода составляет семьдесят процентов от планеты, а суша – тридцать. Изобразим всё это с помощью круговой диаграммы. Нарисуем круг. Он будет изображать планету и соответственно будет равен ста процентам. Затем изобразим семьдесят процентов суши и тридцать процентов воды.
На данной диаграмме мы можем увидеть соотношение воды и суши.
Теперь рассмотрим ещё один пример. Саша тратит на дорогу от дома до школы 10 минут, Таня – 15 минут, Ира – 7 минут и Игорь – 20 минут. Давайте все это изобразим с помощью диаграммы. На оси X напишем имена учащихся, а на оси Y – время, затраченное на дорогу. Затем каждому учащемуся нарисуем столбик по высоте соответствующий времени его пути.
Таким образом мы получили столбчатую диаграмму.
· Графическая информационная модель – это наглядный способ представления объектов и процессов в виде графических изображений.
· Схема – это графическое отображение состава и структуры сложной системы.
· Чертёж – это условное графическое изображение предмета с точным соотношением его размеров, получаемое методом моделирования.
· График – это графическое изображение, которое отображает зависимость одной величины от другой, динамику какого-либо процесса в течение какого-либо периода и много другое.
· Диаграмма – это графическое изображение, которое дает наглядное представление о соотношении каких-либо величин или нескольких значений одной величины, об изменении их значений.
Графические информационные модели
1.3 Графические информационные модели.
Графическая информационная модель – это наглядный способ представления объектов и процессов в виде графических изображений. К ним относятся: чертежи, графики, диаграммы, образные модели, схемы (карты, графы, блок-схемы).
Графические (геометрические) информационные модели передают внешние признаки объекта — размеры, форму, цвет, расположение. В графических информационных моделях для наглядного отображения объектов используются условные графические изображения (образные элементы). Часто графические модели дополняются числами, символами и текстами (знаковыми элементами). В этом случае их называют смешанными моделями.
Схема — это представление некоторого объекта в общих, главных чертах с помощью условных обозначений. Схема – это графическое отображение состава и структуры сложной системы. С помощью схем может быть представлен и внешний вид объекта, и его структура. Схема как информационная модель не претендует на полноту предоставления информации об объекте. С помощью особых приёмов и графических обозначений на ней более рельефно выделяется один или несколько признаков рассматриваемого объекта.

В информатике особое место занимает построение блок-схем. Блок-схемы наглядно отражают алгоритм, т. е. последовательность действий при решении задачи. Они строятся при программировании – создании новых программ.
Карта описывает конкретную местность, которая является для нее объектом моделирования. Это уменьшенное обобщённое изображение поверхности Земли на плоскости в той или иной системе условных обозначений.
Карта создается с определенными целями для определения:
- местоположения населенных пунктов; рельефа местности; расположения автомагистралей; измерения расстояний между реальными объектами на местности
Графики и диаграммы — это информационные модели, которые в наглядной форме представляют числовые и статистические данные.
График — линия, дающая наглядное представление о характере зависимости одной величины (например, пути) от другой (например, времени). График – отображение и визуализация различных процессов (природных, экономических, общественных и технических). График позволяет отслеживать динамику изменения данных.
Диаграмма — графическое изображение, дающее наглядное представление о соотношении каких-либо величин или нескольких значений одной величины, об изменении их значений. Более подробно типы диаграмм и способы их построения будут рассмотрены при изучении электронных таблиц.
Отдельное место среди графических моделей занимают графы.
Графы – замечательные математические объекты, с их помощью можно решать очень много различных, внешне не похожих друг на друга задач. В математике существует целый раздел – теория графов, который изучает графы, их свойства и применение. В информатике по графам строятся программы. В этом параграфе рассмотрены только самые основные понятия, свойства графов и некоторые способы решения задач.
Если объекты некоторой системы изобразить точками (кругами, овалами, прямоугольниками…), а связи между ними — линиями (дугами, стрелками…), то мы получим информационную модель рассматриваемой системы в форме графа. Граф представляет собой набор вершин и соединяющих их ребер. Вершины графа могут быть обозначены буквами, числами, словами…
Если ребра графа указывают направление (представлены стрелками), то граф называют ориентированным (орграфом). Движение в ориентированном графе возможно тольеко в одном направлении (по стрелкам). Связи между объектами – вершинами в таком случае считаются несимметричными. У неориентированного графа связи между объектами – вершинами симметричны.
Одинаковые, но по-разному нарисованные графы, называют изоморфными. У изоморфных графов соединены одни и те же вершины.
Степенью вершины графа называется количество выходящих из нее ребер. Вершина, имеющая четную степень, называется четной вершиной, Вершина, имеющая нечетную степень, называется нечетной вершиной. На рисунке вершины A, B, D – чётные. Их степень равна 2. Вершины С, Е – нечётные. Их степень равна 3.
С понятием степени вершины связана одна из основных теорем теории графов – теорема о чётности числа нечетных вершин.
Теорема: Любой нормальный граф содержит четное число нечетных вершин.
Для иллюстрации рассмотрим задачу.
В городе Маленьком 5 телефонов. Можно ли их соединить проводами так, чтобы каждый телефон был соединен ровно с 3-мя другими?
Решение: Допустим, что такое соединение телефонов возможно. Тогда представим себе граф, в котором вершины обозначают телефоны, а ребра – провода, их соединяющие. Подсчитаем, сколько всего получится проводов. К каждому телефону подключено ровно 3 провода, т. е. степень каждой вершины нашего графа – 3. Чтобы найти число проводов, надо просуммировать степени всех вершин графа и полученный результат разделить на 2 (т. к. каждый провод имеет два конца и при суммировании степеней каждый провод взят 2 раза). (3*5)/2=15/2=7,5
Но это число не целое, то есть количество проводов получится разным. Значит наше предположение о том, что можно соединить каждый телефон ровно с пятью другими, оказалось неверным.
Ответ. Соединить телефоны таким образом невозможно.
Есть еще одно важное понятие, относящееся к графам – понятие связности. Граф называется связным, если любые две его вершины можно соединить путем, т. е. непрерывной последовательностью ребер. Существует целый ряд задач, решение которых основано на понятии связности графа. Граф на рисунке ниже имеет три компоненты связности (состоит из трёх отдельных частей).
Вершина, не имеющая рёбер, называется изолированной вершиной и составляет отдельную компоненту связности. Вершина, имеющая только одно ребро, называется концевой или висячей.
Путь по вершинам и рёбрам графа, в который любое ребро графа входит не более одного раза, называется цепью (1). Цепь, начальная и конечная вершины которой совпадают, называется циклом (2). Дерево (иерархия) – это граф, в котором нет циклов (3), т. е. в нём нельзя из некоторой вершины пройти по нескольким различным рёбрам и вернуться в ту же вершину. Отличительной особенностью дерева является то, что между любыми двумя его вершинами существует единственный путь.



Всякая иерархическая система может быть представлена с помощью дерева. У дерева выделяется одна главная вершина, называемая его корнем. Каждая вершина дерева (кроме корня) имеет только одного предка, обозначенный им объект входит в один класс высшего уровня. Любая вершина дерева может порождать несколько потомков — вершин, соответствующих классам нижнего уровня. Такой принцип связи называется «один-ко-многим». Вершины, не имеющие порождённых вершин, называются листьями.
Например, родственные связи между членами семьи удобно изображать с помощью графа, называемого генеалогическим или родословным деревом.
Граф с циклом называется сетью. Если героев некоторого литературного произведения представить вершинами графа, а существующие между ними связи изобразить рёбрами, то мы получим граф, называемый семантической сетью.
1.3.3 Использование графов при решении задач
Пример 1. Для того чтобы записать все трёхзначные числа, состоящие из цифр 1 и 2, можно воспользоваться графом (деревом).
Дерево можно не строить, если не требуется выписывать все возможные варианты, а нужно просто указать их количество. В этом случае рассуждать нужно так: в разряде сотен может быть любая из цифр (1или 2), в разряде десятков — те же два варианта, в разряде единиц — те же два варианта. Следовательно, число различных вариантов: 2 • 2 • 2 = 8.
В общем случае, если известно количество возможных вариантов выбора на каждом шаге построения графа, то для вычисления общего количества вариантов нужно все эти числа перемножить.
Пример 2. Рассмотрим несколько видоизменённую классическую задачу о переправе.
На берегу реки стоит крестьянин (К) с лодкой, а рядом с ним — собака (С), лиса (Л) и гусь (Г). Крестьянин должен переправиться сам и перевезти собаку, лису и гуся на другой берег. Однако в лодку кроме крестьянина помещается либо только собака, либо только лиса, либо только гусь. Оставлять же собаку с лисой или лису с гусем без присмотра нельзя — собака представляет опасность для лисы, а лиса — для гуся. Как крестьянин должен организовать переправу?
Для решения этой задачи составим граф, вершинами которого будут исходное размещение персонажей на берегу реки, а также всевозможные промежуточные состояния, достигаемые из предыдущих за один шаг переправы. Каждую вершину-состояние переправы обозначим овалом и свяжем рёбрами с состояниями, образованными из неё. Недопустимые по условию задачи состояния выделены пунктирной линией; они исключаются из дальнейшего рассмотрения. Начальное и конечное состояния переправы выделены жирной линией.
На графе видно, что существует два решения этой задачи. Приведём соответствующий одному из них план переправы:
крестьянин перевозит лису; крестьянин возвращается; крестьянин перевозит собаку; крестьянин возвращается с лисой; крестьянин перевозит гуся; крестьянин возвращается; крестьянин перевозит лису.
Пример 3. Рассмотрим следующую игру: сначала в кучке лежит 5 спичек; два игрока убирают спички по очереди, причём за 1 ход можно убрать 1 или 2 спички; выигрывает тот, кто оставит в кучке спичку. Выясним, кто выигрывает при правильной игре — первый (I) или второй (II) игрок.
Игрок I может убрать одну спичку (в этом случае их останется 4) или сразу 2 (в этом случае их останется 3).
Если игрок I оставил 4 спички, игрок II может своим ходом оставить 3 или 2 спички. Если же после хода первого игрока осталось 3 спички, второй игрок может выиграть, взяв две спички и оставив одну.
Если после игрока II осталось 3 или 2 спички, то игрок I в каждой из этих ситуаций имеет шанс на выигрыш.
Таким образом, при правильной стратегии игры всегда выиграет первый игрок. Для этого своим первым ходом он должен взять одну спичку.
На рис. 2.8 представлен граф, называемый деревом игры. На нём отражены все возможные варианты, в том числе ошибочные (проигрышные) ходы игроков.
Контрольные вопросы.
Вопросы и задания выполнить письменно в тетради.
Какие информационные модели относят к графическим? Приведите примеры графических информационных моделей, с которыми вы имеете дело: а) при изучении других предметов; б) в повседневной жизни. Что такое граф? Что является вершинами и рёбрами графа? Укажите на собственном графе-примере. Какой граф называют ориентированным? Какой граф называют взвешенным? Какие графы называют изоморфными?
Что такое степень вершины? Укажите степени вершин в вашем графе. Сформулируйте теорему о чётности числа нечетных вершин. Какой граф называют связным? Изобразите граф с двумя компонентами связности. Какую вершину называют изолированной? Укажите на собственном примере – графе. Какую вершину называют висячей? Укажите на собственном примере – графе. Что такое путь? Что такое цепь? Что такое цикл? Укажите на собственном примере – графе. Что такое граф-дерево? Моделями каких систем могут служить деревья? Приведите пример такой системы. Составьте семантическую сеть по русской народной сказке «Колобок».
Сущность и характеристика графического (наглядного) моделирования
Анастасия Сергиенкова
Сущность и характеристика графического (наглядного) моделирования
Научная статья на тему: «Сущность и характеристика графического (наглядного) моделирования»
Моделирование – наглядно–практический метод обучения. Модель представляет собой обобщенный образ существенных свойств моделируемого объекта (план комнаты, географическая карта, глобус и т. д.).
Метод моделирования, разработанный Д. Б. Элькониным [79], Л. А. Венгером [8], Н. Н. Поддьяковым [50], заключается в том, что мышление ребенка развивают с помощью специальных схем, моделей, которые в наглядной и доступной для него форме воспроизводят скрытые свойства и связи того или иного объекта.
Исследователи (Л. А. Венгер [8], Г. А. Глотова [18]) отмечают, что основы моделирования закладываются в дошкольном возрасте, вырастая из замещений в игре и продуктивных видах деятельности детей (рисование, конструирование и т. д., однако дошкольники осваивают лишь основы моделирования, что проявляется в умении использовать модель в познании разнообразного содержания, выделении и установлении связи «замещаемое – замещающее»; некоторых правил моделирования, замещении содержания, видоизменении готовых моделей.
В. И. Логинова считает, что «под моделированием понимается процесс создания моделей и их использование в целях формирования знаний о свойствах, структуре, отношениях и связях объектов» [15].
Психолог И. Б. Новик характеризует моделирование как «опосредованное практическое или теоретическое исследование объекта, при котором непосредственно изучается не интересующий нас объект, а вспомогательная, искусственная или естественная система, находящаяся в некотором объективном соответствии с познаваемым объектом, способная при его исследовании в конечном итоге получить информацию о самом моделируемом объекте» [3, с. 41].
В настоящее время моделирование рассматривается с разных позиций. В одних работах моделирование выступает как общая интеллектуальная способность (Л. А. Венгер [8], Р. И. Говорова [18], в других – как вид знаково–символической деятельности (Г. А. Глотова [17]). Под знаково–символической деятельностью понимается сложное, системное, многоуровневое, иерархически организованное образование, позволяющее моделировать и преобразовывать во внутреннем плане сознания субъекта объективный мир; процессы конструирования идеализированной предметности и оперирования в ней знаковыми средствами, что играет большую роль, в формировании планирующей функции мышления, необходимой в школьной жизни.
Деятельность со знаково–символическими средствами не ограничивается содержанием, определенным понятием «моделирование», поэтому возникает необходимость выделения других способов оперирования знаково–символическими средствами.
Первым этапом становления знаково–символической деятельности является замещение, оно развивается на протяжении дошкольного детства, качественно изменяясь. По мере освоения ребенком игры, речи, рисования на смену изолированным заместителям приходят их системы. В этих формах деятельности ребенок осваивает разные алфавиты и синтаксисы, если пользоваться терминологией знаковых систем (Н. Г. Салминой, и они сами становятся предметом анализа. Одно и тоже содержание ребенок научается выражать на разных языках – символьном, графическом и т. д. [18].
Второй этап становления знаково–символической деятельности – моделирование. В его основе лежит замещение – возможность переноса значения с одного объекта на другой, возможность репрезентировать одно через другое.
Модели – это формы особых абстракций, в которых существенные отношения объекта закреплены в наглядно–воспринимаемых и представляемых связях и отношениях, вещественных или знаковых элементах [4]. А под моделированием понимается процесс создания моделей и их использование в целях формирования знаний о свойствах, структуре, отношениях, связях объектов. Особенность моделирования как метода обучения в том, что оно делает наглядным скрытые от непосредственного восприятия свойства, связи, отношения объектов, которые являются существенными для понимания фактов, явлений, при формировании знаний, приближающихся по содержанию к понятиям.
Модели условно делятся на три группы
1. Предметные. Они помогают воспроизводить структуру и особенность, внутренние и внешние взаимосвязи реальных объектов и явлений. Это разные предметы и конструкции (макет аквариума, Земли, природных зон «Север», «Лес»).
2. Предметно–схематические модели. Здесь выделенные в объекте познания существенные компоненты и связи между ними обозначаются при помощи предметов–заместителей и графических знаков. Примером простой предметно–схематической модели может служить модель для раскрытия понятия о покровительственной окраске, как проявлении связи животного со средой обитания (лист картона определенной расцветки и фигура животного: если их цвета совпадают, то животное не видно).
3. Графические модели. Они передают обобщенно (условно) признаки, связи и отношения явлений. Примером такой модели может быть календарь погоды, который ведут дети, используя специальные значки–символы для обозначения явлений в неживой и живой природе, а также структуры описательного рассказа об игрушках, транспорте и другие; схемы к рассказам, стихотворениям; наборы схем для графического плана; детские схемы) [25].
Одним из видов графических моделей является мнемотехника. Мнемотехнику в дошкольной педагогике называют по–разному: называет эту методику сенсорно–графическими схемами, – предметно–схематическими моделями, Ефименкова Л. Н. – схемой составления рассказа, мнемотехнику называют также символической аналогией, графической аналогией, пиктограммами [23].
Доступность метода моделирования для дошкольников показана была психологами и педагогами (А. В. Запорожцем [28], Л. А. Венгером [8], Д. Б. Элькониным [80], В. И. Логиновой [40], М. В. Крулехт [34]). Она определяется тем, что в основе моделирования, как уже отмечалось,лежит принцип замещения: реальный предмет может быть замещен в деятельности детей другим предметом, изображением, знаком. Как показали исследования, ребенок рано овладевает замещением объектов в игре, в процессе освоения речи, в формировании природоведческих знаний, конструирования, в изобразительной деятельности, а также в трудовой деятельности.
Третий этап становления знаково–символической деятельности – умственное экспериментирование. Знаково–символическая деятельность приобретает функцию опережающего отражения действительности, прогнозирования, предвидения. Именно здесь максимально полно реализуется функция знаков как усилителей человеческих способностей в реальном мире. Здесь лежат широкие возможности развития креативности, творчества как усиление субъектом самого себя (К. Роджерс) [54].
Кроме того, третий этап характеризуется наличием всех процессов, в которых знаково–символическая деятельность находит свое воплощение: замещение, кодирование, моделирование, схематизация и обобщение (Н. Г. Салмина). Рассмотрим их особенности [18].
Замещение – знаково–символическая деятельность, целью которой является функциональное воспроизведение реальности, использующая любые способы работы. Под замещением, как правило, имеется в виду замены каких–либо объектов или предметов разнозначными предметами.
Кодирование (декодирование) – вид деятельности со знаково–символическими средствами, который заключается в переводе реальности на знаково–символический язык и в последующем декодировании информации. В кодировании могут использоваться любые заместители.
Схематизация – знаково–символическая деятельность, целью которой является ориентировка в реальности (структурирование, выявление связей, осуществляющая одновременно в двух планах с постоянным поэлементным соотнесением символического и реального плана. В схематизации в качестве заместителей выступают схемы. Ребенок «видит» сквозь схемы действительные свойства, осуществляет анализ реальности посредством схемы. Схемы выступают средством ориентировки в действительности.
Моделирование – знаково–символическая деятельность, заключающаяся в получении объективно новой информации за счет оперирования знаково–символическими средствами, в которых представлены структурные, функциональные элементы. Моделирование своим объектом имеет модели. Основная характеристика модели в том, что она является заместителем в широком смысле слова.
Содержание моделирования заключает в себе опосредованнное, практическое или теоретическое обследование объекта, при котором непосредственно изучается не интересующий нас объект, а вспомогательная искусственная или естественная система, находящаяся в некотором объективном соответствии с познаваемым объектом, способная его замещать в определенном отношении, и дающая при его исследовании в конечном итоге, информацию о самом модулируемом объекте [3].
Как выше было изложено, основы моделирования формируются в дошкольном возрасте, вырастая из замещений в игре и продуктивных видах деятельности. Так, разыгрывая тот или иной сюжет в игре, дети моделируют взаимоотношения взрослых людей, а при помощи предметов, используемых в качестве игровых заместителей, создают модели, отображающие взаимосвязи реальных предметов и действий.
Рисунок дошкольника, бесспорно, – наглядная модель изображаемого объекта или ситуации, и не случайно многие исследователи детского рисования называют его схематическим (т. е. модельным) изображением, которое используется в деятельности взрослых.
Еще более явно выступает момент наглядного моделирования в детской конструктивной деятельности. Создаваемые детьми конструкции из строительного материала и различных конструкторов представляют собой объемные модели предметов и ситуаций и затем используются в качестве таковых в процессе сюжетно–ролевых игр.
Однако следует заметить то, что в самых разных видах деятельности дети не просто «символизируют» или обозначают предметы и ситуации, но создают их наглядные модели, устанавливая между отдельными заместителями отношения, адекватные отношениям замещаемых объектов.
Моделирующий характер детской деятельности послужил одним из оснований для выдвижения Л. А. Венгером гипотезы, согласно которой формирование мыслительных способностей ребенка основано на овладении опосредованным решением мыслительных задач. А такой формой опосредования в дошкольном возрасте является наглядное моделирование [8].
Другое основание для разработки гипотезы Л. А. Венгер и его ученики почерпнули из ряда психологических и педагогических исследований, продемонстрировавших понимание дошкольниками различного рода моделей в качестве средства сообщения детям разнообразных знаний. Так, установлено, что дошкольники без всякого предварительного обучения соотносят схематическое изображение лабиринта с реальным лабиринтом и используют его в качестве модели, облегчающей последующую ориентировку в реальном пространстве [8].
Наглядные модели звукового состава используются в качестве одного из основных средств обучения дошкольников грамоте по методике Д. Б. Эльконина [79] и Л. Е. Журовой [27].
Подводя итоги ряда исследований, А. В. Запорожец заключил, что наглядные модели – специфические средства, позволяющие детям усваивать обобщенные знания о некоторых связях и закономерностях явлений деятельности [28].
Наглядное моделирование нашло широкое применение в работах по поэтапному формированию умственных действий и понятий, выступая в качестве одного из главных средств построения ориентировочной основы действий (П. Я. Гальперин [13], Н. Ф. Талызина [62]).
Ведение наглядных моделей в процесс развития речи позволяет логопеду, воспитателю более целенаправленно развивать импрессивную речь детей, обогащать их активный словарь, закреплять навыки словообразования, формировать и совершенствовать умение использовать в речи различные конструкции предложений, описывать предметы, составлять рассказ.
Схематическая наглядность отражает основные качества, свойства, действия предмета или явления в их взаимосвязи и определенной последовательности. Таким образом, она помогает ребенку вычленить главное, основное при характеристике предмета (лица) или последовательности его действий, наглядно демонстрирует каркас, структуру заданного вида рассказа, помогая удерживать в памяти последовательность его частей.В методике развития речи детей дошкольного возраста наиболее признанными являются:
Сериационный ряд. Эта модель представляет собой постепенно увеличивающиеся полоски и кружки разной длины и величины. Сериационный ряд отражает структуру кумулятивной сказки (например, сказка «Репка», в которой происходят многократные, нарастающие повторения действий.
Двигательное моделирование. Двигательное моделирование – воспроизведение основной последовательности действий сказки. Этот вид схематической наглядности представляет собой круги разного цвета и используется при работе со сказками о животных.
Временно – пространственная модель. Эта модель соответствует структуре волшебных сказок. Она представляет собой ряд блоков со стрелочками. Каждый из этих блоков соответствует одному эпизоду сказки. В нем размещаются заместители тех персонажей, которые участвовали в данном эпизоде, а также схематически изображаются некоторые декорации. Стрелки обозначают последовательность перехода от одного эпизода к другому [48].
Схемы для составления описательных рассказов (Т. А. Ткаченко). Эти схемы используются для составления рассказов об игрушках, одежде, посуде, временах года, овощах и фруктах. Эта модель представляет собой лист картона, размером 45х30 см., разделенный на 6–8 квадратов (по количеству характерных признаков предмета или объекта, о которых надо рассказать) [65].
Схемы–рисунки (Л. Соломенникова). Эти схемы можно использовать для обучения пересказу и составлению описательных рассказов. Этот вид схематической наглядности представляет собой полосу картона, разделенную на квадраты (количество квадратов зависит от характерных признаков предмета, объекта) [57].
Эффективность использования наглядного моделирования в развитии связной речи детей с общим недоразвитием речи отмечают В. П. Глухов [19], Т. А. Ткаченко [65], Л. Н. Ефименко [23], В. К. Воробьева [10].
Так, включение наглядных моделей в процесс обучения содействует закреплению понимания значений частей речи и грамматических категорий, развитию понимания логико–грамматических конструкций и целостного речевого высказывания. При этом используемые наглядные модели могут включать стилизованные изображения реальных предметов, символы для обозначения некоторых частей речи («стрелка» вместо глагола, «волнистая линия» вместо прилагательного в моделях предложений и др.); схемы для обозначения основных признаков отдельных видов описываемых предметов, а тех же выполняемых действий по отношению к ним с целью обследования; стилизованные обозначения «ключевых слов» основных частей описательного рассказа.
Применение наглядных моделей способствует более точному и прочному усвоению детьми на практическом уровне отдельных словообразовательных операций. Используя наглядную модель, дети практически усваивают способы образования относительных прилагательных со значением отнесенности к продуктам питания; наглядные схемы ориентируют детей на поиск слов «родственников» в определенном лексико–семантическом поле.
Таким образом, сфера применения наглядного моделирования отнюдь не ограничивается решением учебных задач. Она охватывает самые различные виды детского мышления.
Наглядные модели – специфические средства, позволяющие детям усваивать обобщенные знания о некоторых связях и закономерностях, явлениях действительности. Существуют разные подходы к классификации и использованию наглядного материала, что обусловлено разными задачами обучения и воспитания. Различные виды наглядного моделирования можно применять в обучении детей дошкольного возраста пересказу и различным видам рассказов.
Характеристика общего недоразвития речи ОБЩЕЕ НЕДОРАЗВИТИЕ РЕЧИ Характеристика ОНР по Левиной: ОНР– это такая форма аномалии, под которой следует понимать нарушение всей речевой.
Характеристика на воспитанника ДОУ (младший возраст) Число, месяц, год рождения: Адрес регистрации ребенка: Адрес проживания ребенка: Забелинский Артем поступил в МДОУ на основании путевки.


Конспект НОД по речевому развитию с применением технологии наглядного моделирования и ИКТ «Волшебная страна» Конспект открытой непосредственно образовательной деятельности по речевому развитию в подготовительной группе с применением технологии наглядного.


Сущность самоконтроля и его место в учебной деятельности учащихся младшего школьного возраста Сущность самоконтроля и его место в учебной деятельности учащихся младшего школьного возраста Известно, что учебная деятельность – ведущая.