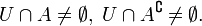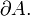Что такое граничные точки отрезка в геометрии

Граничная точка

Смотреть что такое «Граничная точка» в других словарях:

граничная точка — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] граничная точка Такая точка некоторого подмножества A метрического пространства, что любая ее малая окрестность (называется e окрестность) содержит хотя бы одну точку из A и… … Справочник технического переводчика

Граничная точка — [boundary point] такая точка некоторого подмножества A метрического пространства, что любая ее малая окрестность (называется e окрестность) содержит хотя бы одну точку из A и хотя бы одну точку, не принадлежащую A. Например. Г.т., лежащая на… … Экономико-математический словарь

граничная точка — ribinis taškas statusas T sritis fizika atitikmenys: angl. limit point; limiting point vok. Grenzpunkt, m rus. граничная точка, f; предельная точка, f pranc. point limite, m … Fizikos terminų žodynas

Граничная точка — Граница множества это такое множество, что его точки находятся сколь угодно близко как к точкам в множестве, так и к точкам вне множества. Содержание 1 Определение 2 Свойства 3 Примеры 4 См. также … Википедия

граничная точка профиля зуба — граничная точка профиля Общая точка главного или номинального профиля зуба и его переходной кривой. [ГОСТ 16530 83] Тематики передачи зубчатые Обобщающие термины понятия, относящиеся к зубчатому колесупрофиль зуба Синонимы граничная точка профиля … Справочник технического переводчика

граничная точка выхода — Узел, организующий вызов через внешнее соединение. Этот узел является последним в peer группе, кто работает с этим вызовом. [http://www.lexikon.ru/dict/net/index.html] Тематики сети вычислительные EN exit border node … Справочник технического переводчика

граничная точка сети — (МСЭ Т K.66). [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN network boundary pointNBP … Справочник технического переводчика

ИРРЕГУЛЯРНАЯ ГРАНИЧНАЯ ТОЧКА — точка у 0 границы Г области D, для к рой существует такая непрерывная граничная функция f(y)на Г, что обобщенное решение Дирихле задачи в смысле Винера Перрона (см. Перрона метод) и (х)не принимает в точке у 0 граничного значения f(y0), т. е.… … Математическая энциклопедия

верхняя (нижняя) граничная точка однопарного зацепления — Контактная точка профиля зуба, соответствующая началу или окончанию однопарного зацепления, наиболее близкая к его вершине (к его переходной кривой). [ГОСТ 16530 83] Тематики передачи зубчатые Обобщающие термины параметры зубчатой передачи и… … Справочник технического переводчика

Источник

Граничная точка

Грани́ца мно́жества’ — это такое множество, что его точки находятся сколь угодно близко как к точкам в множестве, так и к точкам вне множества.

Содержание

Определение

Множество всех граничных точек множества A называется границей и обозначается

Свойства

Примеры

Рассмотрим числовую прямую со стандартной топологией. Тогда: для :

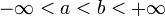
См. также

Полезное

Смотреть что такое «Граничная точка» в других словарях:

граничная точка — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] граничная точка Такая точка некоторого подмножества A метрического пространства, что любая ее малая окрестность (называется e окрестность) содержит хотя бы одну точку из A и… … Справочник технического переводчика

Граничная точка — [boundary point] такая точка некоторого подмножества A метрического пространства, что любая ее малая окрестность (называется e окрестность) содержит хотя бы одну точку из A и хотя бы одну точку, не принадлежащую A. Например. Г.т., лежащая на… … Экономико-математический словарь

граничная точка — ribinis taškas statusas T sritis fizika atitikmenys: angl. limit point; limiting point vok. Grenzpunkt, m rus. граничная точка, f; предельная точка, f pranc. point limite, m … Fizikos terminų žodynas

Граничная точка — множества, точка, в любой окрестности которой находятся как точки, принадлежащие данному множеству, так и не принадлежащие ему. Совокупность всех Г. т. множества составляет его границу. В случае открытых множеств, т. е. множеств, каждая… … Большая советская энциклопедия

граничная точка профиля зуба — граничная точка профиля Общая точка главного или номинального профиля зуба и его переходной кривой. [ГОСТ 16530 83] Тематики передачи зубчатые Обобщающие термины понятия, относящиеся к зубчатому колесупрофиль зуба Синонимы граничная точка профиля … Справочник технического переводчика

граничная точка выхода — Узел, организующий вызов через внешнее соединение. Этот узел является последним в peer группе, кто работает с этим вызовом. [http://www.lexikon.ru/dict/net/index.html] Тематики сети вычислительные EN exit border node … Справочник технического переводчика

граничная точка сети — (МСЭ Т K.66). [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN network boundary pointNBP … Справочник технического переводчика

ИРРЕГУЛЯРНАЯ ГРАНИЧНАЯ ТОЧКА — точка у 0 границы Г области D, для к рой существует такая непрерывная граничная функция f(y)на Г, что обобщенное решение Дирихле задачи в смысле Винера Перрона (см. Перрона метод) и (х)не принимает в точке у 0 граничного значения f(y0), т. е.… … Математическая энциклопедия

верхняя (нижняя) граничная точка однопарного зацепления — Контактная точка профиля зуба, соответствующая началу или окончанию однопарного зацепления, наиболее близкая к его вершине (к его переходной кривой). [ГОСТ 16530 83] Тематики передачи зубчатые Обобщающие термины параметры зубчатой передачи и… … Справочник технического переводчика

Источник

Определение вектора

В статье пойдет речь о том, что такое вектор, что он из себя представляет в геометрическом смысле, введем вытекающие понятия.

Для начала дадим определение:

Вектор – это направленный отрезок прямой.

Исходя из определения, под вектором в геометрии отрезок на плоскости или в пространстве, который имеет направление, и это направление задается началом и концом.

Нулевой вектор

Под нулевым вектором 0 → будем понимать любую точку плоскости или пространства.

Из определения становится очевидным, что нулевой вектор может иметь любое направление на плоскости и в пространстве.

Длина вектора

Под длиной вектора A B → понимается число, большее либо равное 0, и равное длине отрезка АВ.

Понятия модуль вектора и длина вектора равносильны, потому что его обозначение совпадает со знаком модуля. Поэтому длину вектора также называют его модулем. Однако грамотнее использовать термин «длина вектора». Очевидно, что длина нулевого вектора принимает значение ноль.

Коллинеарность векторов

Два вектора лежащие на одной прямой или на параллельных прямых называются коллинеарными.

Два вектора не лежащие на одной прямой или на параллельных прямых называются неколлинеарными.

Следует запомнить, что Нулевой вектор всегда коллинеарен любому другому вектору, так как он может принимать любое направление.

Коллиниарные векторы в свою очередь тоже можно разделить на два класса: сонаправленные и противоположно направленные.

Направление векторов

Считается, что нулевой вектор является сонаправленым к любым другим векторам.

Равные и противоположные векторы

Равными называются сонаправленные вектора, у которых длины равны.

Противопожными называются противоположно направленные вектора, у которых их длины равны.

Введенные выше понятия позволяют нам рассматривать векторы без привязки к конкретным точкам. Иначе говоря, можно заменить вектор равным ему вектором, отложенным от любой точки.

Углы между векторами

Угол φ = ∠ A O B называется углом между векторами a → = O A → и b → = O B → .

Очевидно, что угол между сонаправленными векторами равен нулю градусам (или нулю радиан), так как сонаправленные векторы лежат на одной или на параллельных прямых и имеют одинаковое направление, а угол между противоположно направленными векторами равен 180 градусам (или π радиан), так как противоположно направленные векторы лежат на одной или на параллельных прямых, но имеют противоположные направления.

Перпендикулярными называются два вектора, угол между которыми равен 90 градусам (или π 2 радиан).

Источник

§ 1. Понятие вектора

Эта глава посвящена разработке векторного аппарата геометрии. С помощью векторов можно доказывать теоремы и решать геометрические задачи. Примеры такого применения векторов приведены в данной главе. Но изучение векторов полезно ещё и потому, что они широко используются в физике для описания различных физических величин, таких, например, как скорость, ускорение, сила.

Многие физические величины, например сила, перемещение материальной точки, скорость, характеризуются не только своим числовым значением, но и направлением в пространстве. Такие физические величины называются векторными величинами (или коротко векторами).

Рассмотрим пример. Пусть на тело действует сила в 8 Н. На рисунке силу изображают отрезком со стрелкой (рис. 240). Стрелка указывает направление силы, а длина отрезка соответствует в выбранном масштабе числовому значению силы. Так, на рисунке 240 сила в 1 Н изображена отрезком длиной 0,6 см, поэтому сила в 8 Н изображена отрезком длиной 4,8 см.

Отвлекаясь от конкретных свойств физических векторных величин, мы приходим к геометрическому понятию вектора.

Рассмотрим произвольный отрезок. Его концы называются также граничными точками отрезка.

На отрезке можно указать два направления: от одной граничной точки к другой и наоборот.

Чтобы выбрать одно из этих направлений, одну граничную точку отрезка назовём началом отрезка, а другую — концом отрезка и будем считать, что отрезок направлен от начала к концу.

На рисунках вектор изображается отрезком со стрелкой, показывающей направление вектора. Векторы обозначают двумя заглавными латинскими буквами со стрелкой над ними, например . Первая буква обозначает начало вектора, вторая — конец (рис. 242).

На рисунке 243, а изображены векторы точки А, С, Е — начала этих векторов, а В, D, F — их концы. Векторы часто обозначают и одной строчной латинской буквой со стрелкой над ней: (рис. 243, б).

Для дальнейшего целесообразно условиться, что любая точка плоскости также является вектором. В этом случае вектор называется нулевым. Начало нулевого вектора совпадает с его концом. На рисунке такой вектор изображается одной точкой. Если, например, точка, изображающая нулевой вектор, обозначена буквой М, то данный нулевой вектор можно обозначить так: (рис. 243, а). Нулевой вектор обозначается также символом На рисунке 243 векторы ненулевые, а вектор нулевой.

Длиной или модулем ненулевого вектора называется длина отрезка АВ. Длина вектора (вектора ) обозначается так: . Длина нулевого вектора считается равной нулю:

Длины векторов, изображённых на рисунках 243, а и 243, 6, таковы:

(каждая клетка на рисунке 243 имеет сторону, равную единице измерения отрезков).

Равенство векторов

Прежде чем дать определение равных векторов, обратимся к примеру. Рассмотрим движение тела, при котором все его точки движутся с одной и той же скоростью и в одном и том же направлении.

Скорость каждой точки М тела является векторной величиной, поэтому её можно изобразить направленным отрезком, начало которого совпадает с точкой М (рис. 244). Так как все точки тела движутся с одной и той же скоростью, то все направленные отрезки, изображающие скорости этих точек, имеют одно и то же направление и длины их равны.

Этот пример подсказывает нам, как определить равенство векторов.

Предварительно введём понятие коллинеарных векторов.

Ненулевые векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых; нулевой вектор считается коллинеарным любому вектору.

На рисунке 245 векторы (вектор нулевой) коллинеарны, а векторы а также не коллинеарны.

Сонаправленность векторов и обозначается следующим образом: Если же векторы и противоположно направлены, то это обозначают так: На рисунке 245 изображены как сонаправленные, так и противоположно направленные векторы:

Начало нулевого вектора совпадает с его концом, поэтому нулевой вектор не имеет какого-либо определённого направления. Иначе говоря, любое направление можно считать направлением нулевого вектора. Условимся считать, что нулевой вектор сонаправлен с любым вектором. Таким образом, на рисунке 245 и т. д.

Ненулевые коллинеарные векторы обладают свойствами, которые проиллюстрированы на рисунке 246, а — в.

Дадим теперь определение равных векторов.

Таким образом, векторы и равны, если . Равенство векторов и обозначается так:

Откладывание вектора от данной точки

Если точка А — начало вектора , то говорят, что вектор отложен от точки А (рис. 247). Докажем следующее утверждение:

от любой точки М можно отложить вектор, равный данному вектору , и притом только один.

В самом деле, если — нулевой вектор, то искомым вектором является вектор . Допустим, что вектор ненулевой, а точки А и B — его начало и конец. Проведём через точку M прямую р, параллельную АВ (рис. 248; если M — точка прямой АВ, то в качестве прямой р возьмём саму прямую АВ). На прямой р отложим отрезки MN и MN’, равные отрезку АВ, и выберем из векторов тот, который сонаправлен с вектором (на рисунке 248 вектор ). Этот вектор и является искомым вектором, равным вектору . Из построения следует, что такой вектор только один.

Равные векторы, отложенные от разных точек, часто обозначают одной и той же буквой. Так обозначены, например, равные векторы скорости различных точек на рисунке 244. Иногда про такие векторы говорят, что это один и тот же вектор, но отложенный от разных точек.

Практические задания

738. Отметьте точки А, В и С, не лежащие на одной прямой. Начертите все ненулевые векторы, начало и конец которых совпадают с какими-то двумя из этих точек. Выпишите все полученные векторы и укажите начало и конец каждого вектора.

739. Выбрав подходящий масштаб, начертите векторы, изображающие полёт самолёта сначала на 300 км на юг от города А до В, а потом на 500 км на восток от города В до С. Затем начертите вектор который изображает перемещение из начальной точки в конечную.

740. Начертите векторы так, чтобы:

а) были коллинеарны и

б) были коллинеарны, были не
коллинеарны и

741. Начертите два неколлинеарных вектора и . Изобразите несколько векторов: а) сонаправленных с вектором ; б) сонаправленных с вектором ; в) противоположно направленных вектору ; г) противоположно направленных вектору .

742. Начертите два вектора: а) имеющие равные длины и неколинеарные; б) имеющие равные длины и сонаправленные; в) имеющие равные длины и противоположно направленные. В каком случае полученные векторы равны?

743. Начертите ненулевой вектор и отметьте на плоскости три точки А, В и С. Отложите от точек А, В и С векторы, равные .

Задачи

744. Какие из следующих величин являются векторными: скорость, масса, сила, время, температура, длина, площадь, работа?

745. В прямоугольнике ABCD АВ = 3 см, ВС = 4 см, М — середина стороны АВ. Найдите длины векторов

746. Основание AD прямоугольной трапеции ABCD с прямым углом А равно 12 см, АВ = 5 см, ∠D = 45°. Найдите длины векторов

747. Выпишите пары коллинеарных векторов, которые определяются сторонами: а) параллелограмма MNPQ; б) трапеции ABCD с основаниями AD и ВС; в) треугольника FGH. Укажите среди них пары сонаправленных и противоположно направленных векторов.

748. Диагонали параллелограмма ABCD пересекаются в точке О. Равны ли векторы: а) ; б) ; в) ; г) ? Ответ обоснуйте.

749 Точки S и Т являются серединами боковых сторон MN и LK равнобедренной трапеции MNLK. Равны ли векторы: а) ; б) ; в) ; г) ; д) .

750. Докажите, что если векторы равны, то середины отрезков AD и ВС совпадают. Докажите обратное утверждение: если середины отрезков AD и ВС совпадают, то

751. Определите вид четырёхугольника ABCD, если: и а векторы не коллинеарны.

752. Верно ли утверждение: а) если ; б) если то и коллинеарны; в) если то г) если то д) если

Ответы к задачам

745.

746.

748. а) да; б) нет; в) да; г) нет.

749. а) нет; б) да; в) нет; г) нет; д) да.

751. а) ромб; б) трапеция.

752. а) да; б) да; в) нет; г) нет; д) да.

1 Нетрудно дать и точное определение этих понятий. Например, два ненулевых вектора, лежащие на параллельных прямых, называются сонаправленными (противоположно направленными), если их концы лежат по одну сторону (по разные стороны) от прямой, проходящей через начала. Как сформулировать аналогичное определение для ненулевых векторов, лежащих на одной прямой?

Источник