Что такое группа и подгруппа

Подгруппа

Подгруппа ― подмножество группы , само являющееся группой относительно операции, определяющей .

Подмножество группы является её подгруппой тогда и только тогда, когда:

В случае конечных и, вообще, периодических групп проверка условия 2 является излишней.

Примеры

Связанные определения

Свойства

Полезное

Смотреть что такое «Подгруппа» в других словарях:

подгруппа — подблок, субблок; субгруппа, группа Словарь русских синонимов. подгруппа сущ., кол во синонимов: 2 • группа (98) • … Словарь синонимов

ПОДГРУППА — ПОДГРУППА, подгруппы, жен. Подразделение группы, часть группы. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова

ПОДГРУППА — ПОДГРУППА, ы, жен. Подразделение внутри группы. | прил. подгрупповой, ая, ое. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова

ПОДГРУППА — англ. sub group; нем. Subgruppe. Часть группы, выполняющая либо свои собственные функции, либо функции группы в целом. П. может способствовать функционированию и поддерживанию группы либо ее дезорганизации и разрушению. Antinazi. Энциклопедия… … Энциклопедия социологии

подгруппа — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN subgroup … Справочник технического переводчика

подгруппа — 3.14. подгруппа: Одно или более наблюденных значений признака, используемых для анализа возможностей процесса. Примечания 1. Подгруппу, собранную таким образом, чтобы обеспечить максимальное подобие данных в каждой подгруппе и максимальное… … Словарь-справочник терминов нормативно-технической документации

ПОДГРУППА — подмножество Н группы G, само являющееся группой относительно операции, определяющей G. Подмножество Нгруппы Gявляется ее подгруппой тогда и только тогда, когда: (1) H содержит произведение любых двух элементов из H, (2) H содержит вместе со… … Математическая энциклопедия

подгруппа — pogrupis statusas T sritis chemija apibrėžtis Periodinės elementų sistemos grupės dalis, susidedanti iš elementų, kurių valentinių elektronų šalutiniai kvantiniai skaičiai vienodi. atitikmenys: angl. subgroup rus. подгруппа … Chemijos terminų aiškinamasis žodynas

подгруппа — pogrupis statusas T sritis fizika atitikmenys: angl. subgroup vok. Untergruppe, f rus. подгруппа, f pranc. sous groupe, m … Fizikos terminų žodynas

подгруппа — pogrupis statusas T sritis Kūno kultūra ir sportas apibrėžtis Smulkesnis už grupę vienetas, pvz., grupės dalis, daranti kurį nors fizinį pratimą pratybose. atitikmenys: angl. subgroup vok. Gruppe, f; Vorrunde, f rus. подгруппа … Sporto terminų žodynas

Источник

ПОДГРУППА

Найдено 3 изображения:

подгруппа ж. Подразделение группы, часть группы.

3.14. подгруппа: Одно или более наблюденных значений признака, используемых для анализа возможностей процесса.

1. Подгруппу, собранную таким образом, чтобы обеспечить максимальное подобие данных в каждой подгруппе и максимальное отличие подгрупп между собой называют рациональной подгруппой.

3. Рациональные подгруппы обычно отбирают из последовательных серий значений, иногда применяют случайные выборки.

Смотри также родственные термины:

1.3.9 подгруппа (единиц)

Один из наборов единиц продукции или количество материала, полученные разделением большей группы единиц продукции или большего количества материала

1.3.10 подгруппа (измерений)

Один из наборов групп наблюдений, полученных разделением большей группы наблюдений

3.11 подгруппа испытаний: Совокупность видов испытаний (или одно испытание), проводимых по одному плану испытаний, по результатам которых принимают единую (общую) оценку.

3.48. Подгруппа нефтепродуктов

Совокупность нефтепродуктов, входящих в одну группу и имеющих сходные показатели качества и область применения (бензин автомобильный, дизельное топливо для быстроходных дизелей и судовых газовых турбин, дизельное топливо для автотранспортных тепловозных и судовых дизелей, топливо для реактивных двигателей с дозвуковой скоростью, топливо для реактивных двигателей со сверхзвуковой скоростью и т.д.).

Совокупность нефтепродуктов, входящих в одну группу и имеющих сходные показатели качества и условия применения (бензин автомобильный, бензин авиационный, дизельное топливо для быстроходных дизелей и судовых газовых турбин, дизельное топливо для автотракторных тепловозных и судовых дизелей, топливо печное, топливо газотурбинное, керосин осветительный, топливо для реактивных двигателей с дозвуковой скоростью, топливо для реактивных двигателей со сверхзвуковой скоростью и т. д.)

Теоретико-множественное пересечение любых двух (и любого множества) П. группы G является П. группы G. Пересечение всех П. группы G, содержащих все элементы нек-рого непустого множества М, наз. подгруппой, порожденной множеством М, и обозначается символом <М>. Если Мсостоит из одного элемента а, то <а>наз. циклической П. элемента а. Группа, совпадающая с одной из своих циклических П., наз. циклической группой.

Гомоморфный образ П.- подгруппа. Если группа G₁ изоморфна нек-рой подгруппе H группы G, то говорят, что группа G₁ может быть вложена в группу G. Если даны две группы и каждая из них изоморфна нек-рой истинной П. другой, то отсюда еще не следует изоморфизм самих этих групп. О. А. Иванова.

Источник

Значение слова «подгруппа»

Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека

, само являющееся группой относительно операции, определяющей

является её подгруппой тогда и только тогда, когда:

содержит единичный элемент из

содержит произведение любых двух элементов из

содержит вместе со всяким своим элементом

обратный к нему элемент

В случае конечных и, вообще, периодических групп третье условие является следствием первых двух.

ПОДГРУ’ППА, ы, ж. Подразделение группы, часть группы.

Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека

подгру́ппа

1. выделенная часть или подразделение группы ◆ С совершенствованием техники группы искусств распадаются на всё большее и большее количество подгрупп; дифференциация искусств, как и дифференциация наук, не имеет предела. Андрей Белый, «Смысл искусства», 1907 г. (цитата из НКРЯ) ◆ По обнаружении и обозначении всех мин в намечаемом проходе подгруппа миноискателей выдвигается вперёд и своим огнём прикрывает подгруппу разминирования, которая уничтожает мины взрывом. Сборник боевых документов Великой Отечественной войны. Выпуск 3, 1943–1944 гг. (цитата из НКРЯ) ◆ Из подгруппы тяжёлых инертных газов аргон самый лёгкий. Д. Финкельштейн, «Аргон», 1968 г. // «Химия и жизнь» (цитата из НКРЯ)

2. матем. подмножество группы, само являющееся группой относительно той же бинарной операции и имеющее тот же нейтральный элемент ◆ Проблема нахождения силовской подгруппы данной группы является важной задачей вычислительной теории групп. Для групп перестановок Уильям Кантор доказал, что силовская p—подгруппа может быть найдена за время, полиномиальное от размера задачи (в данном случае это порядок группы, помноженный на количество порождающих элементов). «Теоремы Силова» (цитата из Википедии)

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я стал чуточку лучше понимать мир эмоций.

Вопрос: пустотелый — это что-то нейтральное, положительное или отрицательное?

Источник

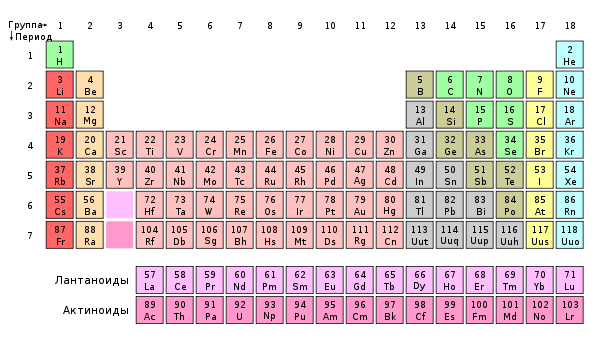
Группа периодической системы

Номер группы определяется количеством электронов на внешней оболочке атома (валентных электронов) и, как правило, соответствует высшей валентности атома.

В короткопериодном варианте периодической системы группы подразделяются на подгруппы — главные (или подгруппы A), начинающиеся с элементов первого и второго периодов, и побочные (подгруппы В), содержащие d-элементы. Подгруппы также имеют названия по элементу с наименьшим зарядом ядра (как правило, по элементу второго периода для главных подгрупп и элементу четвёртого периода для побочных подгрупп). Элементы одной подгруппы обладают сходными химическими свойствами.

С возрастанием заряда ядра у элементов одной группы из-за увеличения числа электронных оболочек увеличиваются атомные радиусы, вследствие чего происходит снижение электроотрицательности, усиление металлических и ослабление неметаллических свойств элементов, усиление восстановительных и ослабление окислительных свойств образуемых ими веществ.

Несмотря на то, что в России и в большинстве стран мира признаётся, что Дмитрий Иванович Менделеев изобрел периодическую таблицу, еще до «холодной войны» в США сформировалось мнение, что первооткрываетелем является Уильям Олдинг.

Нумерация групп

Несмотря на это, продолжают применяться ставшие традиционными системы нумерации с использованием римских цифр и латинских букв, отличающиеся для Америки и Европы.

Современная система нумерации содержит следующие группы (старые системы, Европейская и Американская, приведены в скобках):

Полезное

Смотреть что такое «Группа периодической системы» в других словарях:

Группа периодической таблицы — Группа периодической системы химических элементов последовательность атомов по возрастанию заряда ядра, обладающих однотипным электронным строением. Номер группы определяется количеством электронов на внешней оболочке атома (валентных электронов) … Википедия

Четвёртый период периодической системы — К четвёртому периоду периодической системы относятся элементы четвёртой строки (или четвёртого периода) периодической системы химических элементов. Строение периодической таблицы основано на строках для иллюстрации повторяющихся (периодических)… … Википедия

Первый период периодической системы — К первому периоду периодической системы относятся элементы первой строки (или первого периода) периодической системы химических элементов. Строение периодической таблицы основано на строках для иллюстрации повторяющихся (периодических) трендов в… … Википедия

Второй период периодической системы — Ко второму периоду периодической системы относятся элементы второй строки (или второго периода) периодической системы химических элементов. Строение периодической таблицы основано на строках для иллюстрации повторяющихся (периодических) трендов в … Википедия

Пятый период периодической системы — К пятому периоду периодической системы относятся элементы пятой строки (или пятого периода) периодической системы химических элементов. Строение периодической таблицы основано на строках для иллюстрации повторяющихся (периодических) трендов в… … Википедия

Третий период периодической системы — К третьему периоду периодической системы относятся элементы третьей строки (или третьего периода) периодической системы химических элементов. Строение периодической таблицы основано на строках для иллюстрации повторяющихся (периодических) трендов … Википедия

Седьмой период периодической системы — К седьмому периоду периодической системы относятся элементы седьмой строки (или седьмого периода) периодической системы химических элементов. Строение периодической таблицы основано на строках для иллюстрации повторяющихся (периодических) трендов … Википедия

Шестой период периодической системы — К шестому периоду периодической системы относятся элементы шестой строки (или шестого периода) периодической системы химических элементов. Строение периодической таблицы основано на строках для иллюстрации повторяющихся (периодических) трендов в… … Википедия

Короткая форма периодической системы элементов — Короткая форма таблицы Менделеева основана на параллелизме степеней окисления элементов главных и побочных подгрупп: например, максимальная степень окисления ванадия равна +5, как у фосфора и мышьяка, максимальная степень окисления хрома равна +6 … Википедия

Группа — Сюда перенаправляется запрос «Группировка». На эту тему нужна отдельная статья … Википедия

Источник

Что такое группа и подгруппа

В теории групп рассматриваются пары групп, в которых каждый элемент одной группы принадлежит другой группе. Например, группа целых чисел по сложению и группа рациональных чисел по сложению (каждое целое число рационально).

Другим примером пары групп являются группа отличных от ноля вещественных чисел по умножению и группа отличных от ноля комплексных чисел по умножению (каждое вещественное число можно рассматривать как комплексное число). Или группа положительных вещественных чисел по умножению и группа вещественных чисел по сложению (каждое положительное вещественное число, разумеется, является вещественным числом). В этой паре групп групповые операции в каждой группе различны. Поэтому связь, между такими группами менее тесная, чем в том случае, когда групповые операции одинаковы. В каждом из рассмотренных выше примеров речь шла о некоторой связи между двумя группами. Но группы – это не только наборы элементов и заданной на этом множестве операции. Установление связи между разными группами должно сопровождаться установлением определенной зависимости между групповыми операциями. Если же между операциями в группах никакой зависимости не существует, то, даже располагая самыми подробными сведениями о свойствах исходной, большей группы, можно мало, что сказать о свойствах производной меньшей группы. В тех же случаях, когда операции в двух группах одинаковы (совпадают), операция, заданная на большей группе, уже полностью определяет операцию, заданную на меньшей группе – на подгруппе. Группа называется подгруппой группы , если Н – подмножество множества G и операции g и h совпадают на множестве Н.

Рассмотрим примеры подгрупп, выяснив, каким образом можно сделать вывод о том, образуют ли элементы, принадлежащие тому или иному подмножеству элементов группы, подгруппу или ее не образуют. При этом целесообразно использовать в качестве примера аддитивную группу G, состоящую из целых чисел (положительные и отрицательные, включая ноль), кратных некоторому числу . Пусть , тогда группу G схематично можно представить в виде ряда чисел:

В этой схеме серым цветом подняты значения чисел, которые составляют подгруппу Н и в последующем применительно к теории кодирования станет ясно, что элементы подгруппы Н представляют подмножество разрешенных кодовых комбинаций. По сути, выбирая , выбирают помехоустойчивый код, обладающий теми или иными свойствами, при этом на параметр не накладывается каких-либо особых условий. Заметно, что в приведенном примере между соседними числами кратными находится всего две позиции и если выделенные числа представить аналогом кодовых комбинаций, то между соседними комбинациями не наблюдается существенных различий. Возникает вопрос выбора достаточного расстояния (метрики) между элементами подгруппы Н для их надежного различия.

Интересующее нас подмножество Н должно быть подгруппой, в которой умножение (сложение) совпадает с операцией, заданной на всей группе. На самом подмножестве никакой собственной групповой операции не задается и поэтому она вводиться так, как она определена на исходной группе. Следовательно, в подгруппе остается проверить, не выводит ли за ее пределы операция, определенная на исходной группе, то есть можно ли эту операцию считать групповым умножением (сложением) на интересующем нас подмножестве. Если это действительно так, то обязательно выполняются следующие условия.

1. Произведение (сумма) любых двух элементов подмножества принадлежит подмножеству. Говорят подмножество замкнуто относительно введенной операции. Тем самым на подмножестве Н операция оказывается заданной так, что подмножество становится подгруппой. Более того, операция, превращающая подмножество в подгруппу исходной группы, определена единственным образом. Расширим наше представление о подгруппе и рассмотрим группу целых чисел по сложению. В ней можно выделить следующие подгруппы: множество четных чисел, множество, содержащее только ноль, множество всех целых чисел.

Действительно, сумма двух четных чисел четна, ноль – четное число и число, обратное или противоположное четному числу, также четно. В подгруппе, содержащей только ноль заведомо 0+0=0, сам ноль принадлежит множеству и – 0 = 0. Множество всех целых чисел по определению образуют группу по сложению, т.е. любая группа содержит себя в качестве подгруппы.

Необходимо проверить, существует ли относительно введенной на подмножестве операции левый единичный элемент. Если f – такой элемент, то ff=f. Но поскольку ef=f (e – единичный элемент исходной группы), то ef=ff, откуда, применяя закон сокращения справа, получаем равенство: e=f. Следовательно, если в подмножестве относительно введенной на нем операции существует единичный элемент, то этим элементом может быть только единичный элемент исходной группы. Наоборот, если единичный элемент исходной группы принадлежит выбранному подмножеству, то он, разумеется, является левым единичным элементом относительно определенной на подмножестве операции. Отсюда следует второе условие.

2. Единичный элемент должен принадлежать рассматриваемому подмножеству. Сначала следовало бы проверить, существует ли единичный элемент в выборочном подмножестве. При этом достаточно воспользоваться тем, что этим элементом может быть только единичный элемент исходной группы, и поэтому осуществить поиск путем проверки принадлежности одного вполне определенного элемента группы выбранному подмножеству.

Рассмотрим группу рациональных чисел по сложению. В ней можно выделить следующую подгруппу: множество целых чисел, так как сумма двух целых чисел – целое число, ноль – целое число и любое число, противоположное целому (то есть равное целому числу с обратным знаком) является – также целое. При этом единичный элемент ноль принадлежит как исходной группе рациональных чисел, так и подгруппе целых чисел.

Наконец, следует проверить, для каждого ли элемента подмножества существует принадлежащий подмножеству обратный элемент (относительно определенной на подмножестве операции). Поскольку достоверно известно, что единичный элемент исходной группы должен принадлежать подмножеству, то элемент, обратный любому элементу подмножества, совпадает с элементом, обратным этому элементу в исходной группе. Это положение определяет третье условие.

3. Вместе с каждым элементом подмножество должно содержать обратный элемент. Таким образом, пара образует подгруппу группы в том и только в том случае, если H – подмножество множества G, удовлетворяющее условиям 1,2 и 3 (по определению операция h совпадает с операцией g на Н).

Под данное определение попадают все подгруппы аддитивной, то есть со сложением в качестве групповой операции, группы целых чисел, так как выполнение всех трех условий «гарантировано» тем, что они выполнены в группе целых чисел.

Пример последней подгруппы важен с точки зрения теории построения двоичных помехоустойчивых кодов, поскольку в системе мягкого декодирования при использовании фазовой модуляции принято через значение – 1 представлять бит равный единице, а через значение + 1 бит равный нолю.

Рассмотренные примеры позволяют установить следующее.

1. Все группы содержат в качестве подгруппы множество, состоящее только из единичного элемента. Такая подгруппа называется единичной подгруппой.

2. Любая группа содержит себя в качестве подгруппы.

3. Во всякой группе все подгруппы любой подгруппы являются в то же время подгруппами исходной группы.

Единичная подгруппа и вся группа называются тривиальными подгруппами, а все остальные подгруппы называются истинными подгруппами.

Как показывают примеры, элементы каждой подгруппы обычно обладают каким-нибудь отличительным свойством. Иногда все элементы, входящие в подгруппу, удается «назвать поименно». К последнему способу построения подгруппы можно прибегнуть в том случае, если подгруппа содержит конечное число элементов и проще перебрать все ее элементы, чем найти их отличительный признак.

Если подгруппа задана каким-то свойством, то не составляет особого труда определить, обладает ли этим свойством единичный элемент. Как правило, единичный элемент обладает всеми указанными свойствами. Действительно, из двух других условий следует, что единичный элемент принадлежит рассматриваемому подмножеству. Таким образом, по существу необходимо проверить лишь два условия: замкнутость относительно умножения и взятия обратного элемента. Если группа конечна, то есть содержит конечное число элементов, то достаточно проверить одно из этих условий.

Если некоторое подмножество элементов конечной группы содержит единичный элемент и замкнуто относительно умножения, то оно является подгруппой. Для представления всех элементов мультипликативной (аддитивной) группы в компактной форме прибегают к отображению группы в виде матрицы размерности , где – любое натуральное число, которое определяет порядок (число элементов) подгруппы . Значение , определяющее число различных смежных классов в разложении группы по подгруппе получило название индекса в . Обозначим элементы группы через , а элементы подгрупп – через и рассмотрим таблицу, в которой первая строка состоит из элементов подмножества , при этом единичный элемент в этой строке будет находиться слева, т.е. первым, а любой элемент может появиться в строке только один раз. Первым элементом второй строки в матрице может быть любой элемент группы, не входящий в первую строку, а все остальные элементы получаются умножением слева (сложением) всех элементов подгруппы на первый элемент строки. Аналогично образуются третья и все последующие строки вплоть до строки с номером , пока каждый элемент группы не войдет в матрицу.

Совокупность элементов в строке этой матрицы называются левым смежным классом, а если группа коммутативна, то просто смежным классом. Элементы первого столбца матрицы называются образующим смежного класса. Таким образом, матрица задает разложение группы на смежные классы.

(1.16)

Пусть мультипликативная группа G содержит n элементов, а подгруппа Н – элементов. Правому смежному классу На принадлежат элементы вида ха, где х – произвольный элемент подгруппы Н. Так как элементов х может быть не больше элементов, чем элементов в подгруппе Н, то смежный класс На содержит не больше, чем подгруппа Н. Но все элементы вида ха различны (это следует из закона сокращения), поэтому смежный класс На содержит ровно столько элементов, сколько содержит их подгруппа Н. Если число правых смежных элементов равно m, то общее число элементов группы равно mq, так как каждый из m смежных классов содержит по q элементов. Но соотношение n = mq означает, что число q – делитель числа n, то есть порядок конечной группы всегда делится на порядок любой подгруппы.

(порядок )(индекс в ) = порядок .

Этот факт известен как теорема Лагранжа [4]. Порядок любого элемента конечной группы является делителем порядка группы. Теорема устанавливает довольно жесткие пределы для существования подгрупп данной группы.

Рассматривая образование матрицы, применительно к аддитивной группе целых чисел и положив вновь , получаем новое и более компактное их представление.

(1.17)

Смежный класс, содержащий число 0, представляет собой не что иное, как выбранную подгруппу, то есть состоит из чисел, делящихся на 3. Обозначим его . Элементы смежного класса, содержащего число 1, получим, прибавив по 1 к числам, делящимся на 3. Все числа, образующие новый смежный класс, при делении на 3 дают остаток 1. Обозначим этот смежный . Аналогичным образом можно убедиться в том, что смежный класс, которому принадлежит число 2, состоит из чисел, дающих при делении на 3 остаток 2.Обозначим этот смежный класс .

Заметно, что смежные классы с образующими и формируют те числа представленного выше ряда, которые не кратны . Поэтому в теории кодирования образующие смежных классов, отличные от ноля трактуются как образцы ошибок.

Поскольку всякое целое число (в том числе и отрицательное) при делении на 3 дает в остатке 0, 1 или 2, то других смежных классов при не существует. Таким образом, ответ на вопрос, какому из смежных классов принадлежит сумма двух чисел, зависит не от самих чисел, а от того, какие остатки они дают при делении на 3. Например, если одно из двух чисел при делении на 3 дает остаток 1, а другое – остаток 2, то их сумма всегда будет делиться на 3.

Подгруппа H группы G называется нормальным делителем, или инвариантной подгруппой, если для любых двух смежных классов aH и bH по подгруппе H произведение произвольного элемента из класса aH и произвольного элемента из класса bH всегда принадлежит одному и тому же смежному классу abH.

В коммутативных группах всякая подгруппа является нормальным делителем. Подгруппа H группы G является нормальным делителем в том и только в том случае, если каждый левый смежный класс по H совпадает с некоторым правым смежным классом по H (и наоборот).

Отличительный признак нормального делителя, состоящий в том, что всякий левый смежный класс по нормальному делителю H является одновременно и правым смежным классом, можно сформулировать следующим образом: для произвольного элемента группы G смежные классы aH и Ha совпадают. Для этого достаточно, чтобы все элементы смежного класса aH (разумеется, при любом элементе группы G) принадлежали смежному классу Ha.

Если подгруппа группы нормальная, то можно ввести операцию над смежными классами, так, что получится новая группа, элементами которой будут смежные классы. Эта группа получила название факторгруппы и обозначается как .

Источник