Что такое группировка слагаемых

Группировка слагаемых и множителей, правило, примеры.

К суммам трех и большего количества слагаемых относится тождественное преобразование, имеющее название группировка слагаемых. Аналогичный вид преобразований существует и для произведений трех, четырех и т.д. множителей, называемый группировкой множителей. В этой статье мы разберем правила группировки слагаемых и множителей, и рассмотрим применение этих правил на примерах.

Навигация по странице.

Группировка слагаемых, примеры

В числовых и буквенных выражениях, содержащих суммы трех и большего количества слагаемых, можно выполнять группировку слагаемых. Что же понимают под этим термином?

Под группировкой слагаемых подразумевается совместное рассмотрение нескольких слагаемых в сумме. Иными словами, группировка слагаемых – это объединение слагаемых в группу.

Существует правило группировки слагаемых: сначала в исходной сумме выполняется перестановка слагаемых так, чтобы группируемые слагаемые оказались рядом, после чего они заключаются в скобки.

Прежде чем перейти к рассмотрению примеров, поясним, на чем основано приведенное правило группировки слагаемых. Оно базируется на переместительном и сочетательном свойстве сложения.

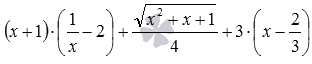
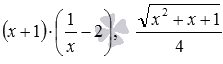
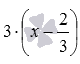
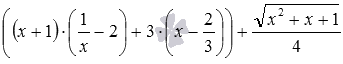
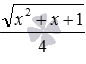
Следует заметить, что часто основные трудности с группировкой слагаемых заключаются не в самой группировке, а в том, чтобы разглядеть в исходном выражении сумму и составляющие ее слагаемые. Особенно это касается громоздких выражений. Когда слагаемые найдены, их группировка не вызывает проблем. Например, выражение представляет собой сумму трех слагаемых и . После того, как мы определили эти слагаемые, мы можем сгруппировать, например, первое слагаемое с третьим, при этом получим выражение . Кстати, в дроби под знаком корня находится сумма трех слагаемых, в которой тоже можно провести группировку.

Группировка слагаемых широко применяется для рационального вычисления значений выражений, при упрощении выражений и при решении многих других математических задач. К примеру, при вычислении значения выражения 1/3+2/7+2/3+3/7 удобно сгруппировать дроби с одинаковым знаменателем, что упрощает и ускоряет вычисления: 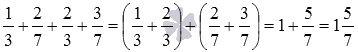. К слову, на группировке слагаемых базируется один из методов разложения многочлена на множители.

Группировка множителей, примеры

Группировка множителей по своему смыслу аналогична группировке слагаемых, только она проводится не в суммах, а в произведениях. Так под группировкой множителей в произведении понимают объединение нескольких множителей в группу.

Группировка множителей проводится по правилу, которое также аналогично правилу группировки слагаемых: группируемые множители переставляются в произведении так, чтобы они оказались рядом одно за другим, после чего они заключаются в скобки. Теоретической базой этого правила являются переместительное и сочетательное свойство умножения.

Источник

Способ группировки

Кроме вынесения общего множителя за скобки существует еще один способ разложения многочлена на множители — способ группировки.

Этот способ разложения на множители считается более сложным, поэтому перед его изучением, убедитесь, что вы уверенно выносите общий множитель за скобки.

Чтобы разложить многочлен на множители способом группировки, необходимо сделать следующее.

Рассмотрим пример разложения многочлена на множители способом группировки.

Примеры способа группировки

Рассмотрим пример. Требуется разложить многочлен на множители, используя способ группировки.

Первый способ

Обратим внимание, что в двух одночленах повторяется « y 2 » и « z 2 ». Подчеркнем повторяющиеся одночлены и запишем их друг за другом. Затем вынесем общий множитель у каждой группы одночленов.

48x z 2 + 32x y 2 − 15 z 2 − 10 y 2 = 48x z 2 − 15 z 2 + 32x y 2 − 10 y 2 = 3z 2 (16x − 5) + 2y 2 (16x − 5) =
= (16x − 5)(3z 2 + 2y 2 )

Второй способ

Запишем пример еще раз. Теперь обратим внимание, что в первых двух одночленах повторяется « x ». Подчеркнем повторяющиеся одночлены. Вынесем общий множитель у каждой группы одночленов.

48 x z 2 + 32 x y 2 − 15z 2 − 10y 2 = 16x(3z 2 + 2y 2 ) − 5(3z 2 + 2y 2 ) = (3z 2 + 2y 2 )(16x − 5)

В итоге получился такой же ответ, как и при первом способе.

Рассмотрим еще один пример разложения многочлена способом группировки.

Смена знаков в скобках

Иногда для вынесения общего многочлена требуется сменить все знаки одночленов в скобках на противоположные.

Для этого за скобки выносится знак « − », а в скобках у всех одночленов меняются знаки на противоположные.

2ab 2 − 3x + 1 = −( − 2ab 2 + 3x − 1)

Рассмотрим пример способа группировки, где для вынесения общего многочлена, нам потрубуется выполнить смену знаков в скобках.

Источник

Разложение многочлена способом группировки

Основные понятия

Мы знаем, что слово «множитель» происходит от слова «умножать».

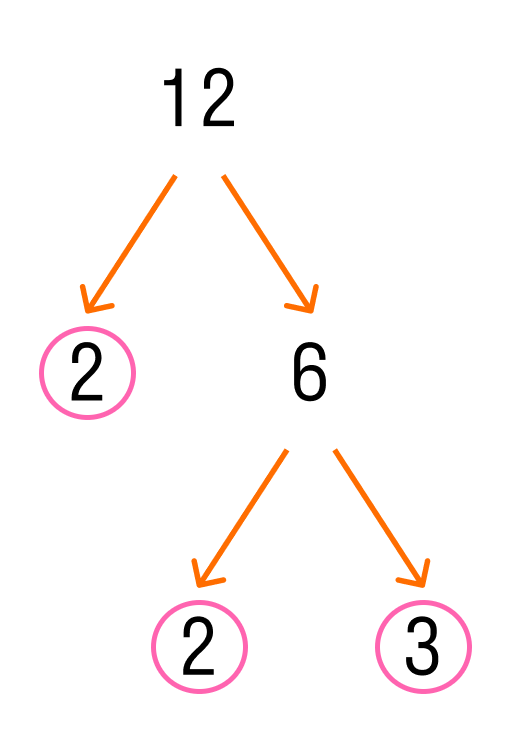
Возьмем, например, число 12. Чтобы разложить его на множители, нужно написать его по-другому, а именно в виде «произведения» множителей.

Число 12 можно получить, если умножить 2 на 6. А 6 можно представить, как произведение 2 и 3. Вот так:

Так выглядит пошаговое разложение на множители. Числа, которые обведены в кружок на картинке — это множители, которые дальше разложить уже нельзя.

Разложение многочлена на множители — это преобразование многочлена в произведение, которое равно данному многочлену.

5 способов разложения многочлена на множители

Способ группировки множителей

Разложение на множители методом группировки возможно, когда многочлены не имеют общего множителя для всех членов многочлена.

Этот способ применяется в тех случаях, когда многочлен удается представить в виде пар слагаемых таким образом, чтобы из каждой пары можно было выделить один и тот же множитель. Этот общий множитель можно вынести за скобку. И тогда исходный многочлен будет представлен в виде произведения, что значительно облегчает задачу.

Разложить на множители методом группировки можно в три этапа:

Объединить члены многочлена в группы можно по-разному. И не всегда группировка может быть удачной для последующего разложения на множители. В таком случае нужно продолжить эксперимент и попробовать объединить в группы другие члены многочлена.

Чтобы понять эти сложные выражения, применим правило группировки множителей при решении примеров. Рассмотрим два способа.

Заметим, что в первой группе повторяется p, а во второй — d.

Вынесем в первой группе общий множитель p, а во второй общий множитель d.

Вынесем его за скобки:

Группировка множителей выполнена.

Заметим, что в первой группе повторяется u, а во второй — b.

Вынесем в первой группе общий множитель u, а во второй общий множитель b.

Заметим, что общий множитель (p + d).

Вынесем его за скобки:

Группировка множителей выполнена.

От перестановки мест множителей произведение не меняется, поэтому оба ответа верны:

Вот так работает алгоритм разложения многочлена на множители способом группировки. Продолжим практиковаться на примерах.

Иногда для вынесения общего многочлена нужно заменить все знаки одночленов в скобках на противоположные. Для этого за скобки выносится знак минус, а в скобках у всех одночленов меняем знаки на противоположные.

Проверим как это на следующем примере.

Курсы ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Источник

Презентация по математике на тему»Группировка слагаемых»(4 класс)

Описание презентации по отдельным слайдам:

Один гусь и одна утка весят вместе столько же, сколько весит один поросенок. Гусь весит 7 кг, поросенок 12 кг. Определите вес утки? 5 кг

Около школы строят дом. 7 этажей уже построили. Планируют, что это будет девятиэтажный дом. На сколько этажей больше уже построили, чем еще осталось построить? на 5 этажей

Петя хотел прибавить к 12 какое-то число. Когда он сложил эти числа, то получил 63, но оказалось, что он ошибся, его ответ на 1 больше того, который является правильным. Какое число прибавлял Петя? 50

205, 210, 215,… 900,890,880,… 35 см,70 см,140 см,… Чистописание Пропишите до конца строчки, установив закономерность.

205, 210, 215, 220,225,230,235,240,245,250 Чистописание

35 см,70 см,140 см,280 см, 560 см Чистописание

до 1 тонны 580 кг 520 кг 150 кг 860 кг Дополните

до 1 километра 870 м 500 м 320 м 450 м

Слагаемое Слагаемое Сумма Как называются компоненты при сложении?

ПЕРЕМЕСТИТЕЛЬНОЕ СВОЙСТВО СЛОЖЕНИЯ 127+643 = 644+123

73+138+107+50+42= Найдите значение выражения 410

(73+107)+(138+42)+50=180+180+50= Найдите значение выражения 410

группировать Математики говорят: слагаемые можно не только переставлять, но и

ГРУППИРОВАТЬ-объединять, соединять в группу, группы по каким либо признакам.

ГРУППИРОВКА СЛАГАЕМЫХ ЭТО ПРИЁМ РАЦИОНАЛЬНЫХ ВЫЧИСЛЕНИЙ

Тема урока-ГРУППИРОВКА СЛАГАЕМЫХ КАК РАЦИОНАЛЬНЫЙ ПРИЁМ ВЫЧИСЛЕНИЙ

Как в математике называется действие, когда слагаемые объединяют в группы? ГРУППИРОВКА СЛАГАЕМЫХ

Что такое группировка слагаемых? объединение в группы слагаемых при сложении

С какой целью мы группируем слагаемые? чтобы удобнее было вычислять

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-748827

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Путин призвал повышать уровень общей подготовки в колледжах

Время чтения: 1 минута

В Хабаровске родители смогут заходить в школы и детсады только по QR-коду

Время чтения: 1 минута

Поставщики интернета для школ будут работать с российским оборудованием

Время чтения: 1 минута

Итоговое сочинение успешно написали более 97% выпускников школ

Время чтения: 2 минуты

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Группировка слагаемых

Группировка слагаемых — это объединение слагаемых в группы с помощью скобок. При группировке слагаемых обычно изменяется порядок их следования в сумме для удобства вычислений.

Метод группировки слагаемых можно применять к суммам, состоящим из трёх и более слагаемых. Группировку можно разбить на три последовательных действия:

Рассмотрим нахождение значения выражения, изображённого на картинке:

Можно просто сначала сложить первые два слагаемых, к полученной сумме прибавить третье слагаемое, а к полученному результату затем прибавить четвёртое слагаемое:

15 + 27 + 55 + 13 = 42 + 55 + 13 = 97 + 13 = 110,

но в данном случае значение выражения будет легче найти, если сначала сгруппировать слагаемые так, чтобы в сумме они давали круглые числа:

15 + 27 + 55 + 13 = (15 + 55) + (27 + 13) = 70 + 40 = 110.

Приём группировки слагаемых обычно используется для упрощения вычислений.

Пример. Вычислить значение выражений, используя приём группировки слагаемых.

3) 340 + 114 + 60 + 26;

4) 154 + 235 + 13 + 115 + 46.

1) 248 + 123 + 52 + 7 = ( 248 + 52) + ( 123 + 7) = 300 + 130 = 430;

2) 101 + 67 + 19 + 3 = ( 101 + 19) + ( 67 + 3) = 120 + 70 = 190;

3) 340 + 114 + 60 + 26 = ( 340 + 60) + ( 114 + 26) = 400 + 140 = 540;

4) 154 + 235 + 13 + 115 + 46 = ( 154 + 46) + ( 235 + 115) + 13 = 200 + 350 + 13 = 563.

Источник