Что такое начала евклида
Начала Евклида
Не снимайте пометку о выставлении на переименование до окончания обсуждения.
Дата постановки — 29 августа 2012.
Прокл сообщает (ссылаясь на Евдема), что подобные сочинения создавались и до Евклида: «Начала» были написаны Гиппократом Хиосским, а также платониками Леонтом и Февдием. Но эти сочинения, по-видимому, были утрачены ещё в античности.
«Начала» оказали огромное влияние на развитие математики вплоть до Новейшего времени. Книга переведена на множество языков мира. По количеству переизданий «Начала» не имеют себе равных среди светских книг.
Содержание
Краткий обзор содержания
В «Началах» излагаются планиметрия, стереометрия, арифметика, отношения по Евдоксу. В классической реконструкции Гейберга весь труд состоит из 13 книг. К ним традиционно присоединяют две книги о пяти правильных многогранниках, приписываемые Гипсиклу Александрийскому и школе Исидора Милетского.
Изложение в «Началах» ведётся строго дедуктивно. Каждая книга начинается с определений. В первой книге за определениями идут аксиомы и постулаты. Затем следуют предложения, которые делятся на задачи (в которых нужно что-то построить) и теоремы (в которых нужно что-то доказать). Определения, аксиомы, постулаты и предложения пронумерованы, например, I def. 2 — второе определение первой книги.
Первая книга
Первая книга начинается определениями, из которых первые семь (I def. 1-7) гласят:
Комментаторы эпохи Возрождения предпочитали говорить, что точка есть место без протяжения. Современные авторы, напротив, признают невозможность определения основных понятий, и Давид Гильберт начинает «Основания геометрии» [6] так:
Мы мыслим три различные системы вещей: вещи первой системы мы называем точками и обозначаем 
За определениями Евклид приводит постулаты (I post. 1-5):
Наиболее интересен в аксиоматике Евклида последний, знаменитый пятый постулат. Среди других, интуитивно очевидных постулатов, он нарочито чужероден, его громоздкая формулировка закономерно вызывает некоторое чувство протеста и желание отыскать для него доказательство. Такие доказательства уже в древности пытались построить Птолемей и Прокл; а в Новое время из этих попыток развилась неевклидова геометрия. Следует отметить, что первые 28 теорем I книги относятся к абсолютной геометрии, то есть не опираются на V постулат.
За постулатами следуют аксиомы (I ax. 1-9), которые имеют характер общих утверждений, относящихся в равной мере как к числам, так и к непрерывным величинам:
В скобки взяты аксиомы, принадлежность которых Евклиду Гейберг, автор классической реконструкции текста «Начал», счёл сомнительной. I post. 4 и 5 в ряде списков выступают как I ax. 10 и 11 соответственно.
За аксиомами следуют три теоремы, представляющие собой задачи на построение, давно вызывающие споры. Так I prop. 2 предлагает «от данной точки отложить прямую, равную данной прямой». Нетривиальность этой задачи состоит в том, что Евклид не переносит отрезок на прямую соответствующим раствором циркуля, полагая такую операцию недозволенной, и использует I post. 3 в неожиданно узком смысле.
Затем рассматриваются различные случаи равенства и неравенства треугольников; теоремы о параллельных прямых и параллелограммах; так называемые «местные» теоремы о равенстве площадей треугольников и параллелограммов на одном основании и под одной высотой. Заканчивается I книга теоремой Пифагора.
Обзор содержания книг II—XIII
II книга — теоремы так называемой «геометрической алгебры».
IV книга — предложения о вписанных и описанных многоугольниках, о построении правильных многоугольников.
V книга — общая теория отношений, разработанная Евдоксом Книдским.
VI книга — учение о подобии геометрических фигур. Эта книга завершает евклидову планиметрию.
VII, VIII и IX книги посвящены теоретической арифметике. Евклид в качестве чисел рассматривает исключительно натуральные числа; для него «Число есть совокупность единиц». Здесь излагаются теория делимости и пропорций, доказывается бесконечность множества простых чисел, приводится алгоритм Евклида для нахождения наибольшего общего делителя двух чисел, строятся чётные совершенные числа. Евклид доказывает также формулу для суммы геометрической прогрессии.
X книга — классификация несоизмеримых величин. Это самая объёмная из книг «Начал».
XI книга — начала стереометрии: теоремы о взаимном расположении прямых и плоскостей; теоремы о телесных углах, объём параллелепипеда и призмы, теоремы о равенстве и подобии параллелепипедов.
XII книга — теоремы о пирамидах и конусах, доказываемые с помощью метода исчерпывания. Здесь доказывается, например, теорема о том, что объём конуса составляет одну треть от объёма цилиндра с теми же основанием и высотой.
XIII книга — построение правильных многогранников; доказательство того, что существует ровно пять правильных многогранников.
Евклид нигде в книге не ссылается на других греческих математиков, хотя несомненно опирается на их результаты. Историки науки [9] [10] показали, что прототипом для труда Евклида послужили более ранние сочинения античных математиков:
В целом содержание «Начал» покрывает значительную часть античной теоретической математики. Однако некоторая часть известного древнегреческим математикам материала осталась вне этого труда — например, конические сечения (Евклид посвятил им отдельный труд, который не сохранился), длина окружности, теория приближённых вычислений.
Манускрипты и издания «Начал»
Греческий текст «Начал»
При раскопках античных городов найдено несколько папирусов, содержащих небольшие фрагменты «Начал» Евклида. Самый известный был найден в «городе папирусов» Оксиринхе в 1896—1897 и содержит формулировку II prop. 5 с рисунком. [11]
Греческий текст «Начал» Евклида известен по византийским манускриптам, из них самые известные:
На их основе, а также с учётом арабских переводов «Начал» (IX век и далее) оригинальный текст был реконструирован датским историком науки Гейбергом в конце XIX века, его методы подробно описаны Хизом (T. L. Heath). [12]
Гейберг использовал в своей реконструкции 8 греческих манускриптов, датируемых сейчас IX—XI веками. Из этих манускриптов семь в своем заглавии имеют пометку «из издания Теона» или «из лекций Теона» и поэтому называются Теоновскими. Ватиканский манускрипт такой пометки не имеет и считается неподверженным редакции Теона. Теоновские манускрипты разнятся между собой, и общих признаков, отличающих их от ватиканского манускрипта, немного (наиболее существенный — концовка IV книги). На полях манускриптов имеются многочисленные комментарии, взятые частично из комментариев Прокла, которые вписывают «Начала» в контекст греческой культуры, напр., сообщается о том, что Пифагор, открыв свою теорему, принес в жертву быков.
История обретения византийских манускриптов темна. Вероятно, они попали в Европу ещё в XVI веке, но не были опубликованы. В первом издание греческого текста, осуществленном Йоханом Хервагеном (Johann Herwagen) между 1533 и 1558 под редакцией Симона Гринера (Simon Gryner, он же Grynaeus, профессор греческого в базельском университете), использованы манускрипты, которые, по мнению Гейберга, представляют собой весьма плохие копии XVI века. Лишь в 1808 Пейрар (F. Peyrard) во время наполеоновских экспроприаций нашел три манускрипта в Ватикане и среди них важнейший ватиканский.
Латинский текст «Начал»
Русские переводы
Первое издание «Начал» на русском языке произошло в 1739 году; книга вышла в Петербурге под названием «Евклидовы элементы из двенадцати нефтоновых книг выбранныя и в осьмь книг через профессора мафематики Андрея Фархварсона сокращенныя, с латинского на российский язык хирургусом Иваном Сатаровым преложенныя». [18] Перевод выполнил И. П. Сатаров под руководством шотландского математика Генри Фарварсона (Henry Fargwarson). [19] Имя Ньютона («Нефтона») в названии упомянуто, возможно, в рекламных целях, к содержанию книги он никакого отношения не имеет. Перевод был сделан с сокращённого французского издания «Начал» А. Такэ (A. Tacquet). [18] Немного позднее вышли ещё 2 перевода, также сокращённые до 8 книг:
Последнее по времени полное академическое издание было опубликовано в 1949-1951 годах, перевод с греческого и комментарии Д. Д. Мордухай-Болтовско́го.
Всемирное распространение
На китайском языке первые 6 книг «Начал» издал Маттео Риччи во время своей миссии в Китае (1583—1610). Полный перевод, выполненный А.Вайли, вышел с хвалебным предисловием Цзэн Гофаня, написанным в 1865 году.
Тексты «Начал»
В сети доступны следующие манускрипты и печатные издания «Начал»:
Начала Евклида
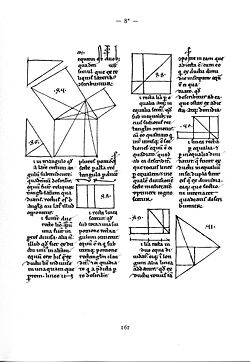
Ватиканский манускрипт (Vat. 190), т.2, 207v — 208r. Euclid XI prop. 31, 32 и 33.
«Начала» оказали огромное влияние на развитие математики вплоть до Новейшего времени. Книга переведена на множество языков мира. По количеству переизданий «Начала» не имеют себе равных среди светских книг.
Содержание
Краткий обзор содержания
Изложение в «Началах» ведётся строго дедуктивно. Каждая книга начинается с определений. В первой книге за определениями идут аксиомы и постулаты. Затем следуют предложения, которые делятся на задачи (в которых нужно что-то построить) и теоремы (в которых нужно что-то доказать). Определения, аксиомы, постулаты и предложения пронумерованы, например, I def. 2 — второе определение первой книги.
Первая книга
Первая книга начинается определениями, из которых первые семь (I def. 1-7) гласят:
Комментаторы эпохи Возрождения предпочитали говорить, что точка есть место без протяжения. Современные авторы, напротив, признают невозможность определения основных понятий, и Давид Гильберт начинает «Основания геометрии» [6] так:
Мы мыслим три различные системы вещей: вещи первой системы мы называем точками и обозначаем 
За определениями Евклид приводит постулаты (I post. 1-5):
За постулатами следуют аксиомы (I ax. 1-9), которые имеют характер общих утверждений, относящихся в равной мере как к числам, так и к непрерывным величинам:
В скобки взяты аксиомы, принадлежность которых Евклиду Гейберг, автор классической реконструкции текста «Начал», счёл сомнительной. I post. 4 и 5 в ряде списков выступают как I ax. 10 и 11 соответственно.
За аксиомами следуют три теоремы, представляющие собой задачи на построение, давно вызывающие споры. Так I prop. 2 предлагает «от данной точки отложить прямую, равную данной прямой». Нетривиальность этой задачи состоит в том, что Евклид не переносит отрезок на прямую соответствующим раствором циркуля, полагая такую операцию недозволенной, и использует I post. 3 в неожиданно узком смысле.
Обзор содержания книг II—XIII
II книга — теоремы так называемой «геометрической алгебры».
V книга — общая теория отношений, разработанная Евдоксом Книдским.
VI книга — учение о подобии геометрических фигур. Эта книга завершает евклидову планиметрию.
X книга — классификация несоизмеримых величин. Это самая объёмная из книг «Начал».
XI книга — начала стереометрии: теоремы о взаимном расположении прямых и плоскостей; теоремы о телесных углах, объём параллелепипеда и призмы, теоремы о равенстве и подобии параллелепипедов.
XIII книга — построение правильных многогранников; доказательство того, что существует ровно пять правильных многогранников.
Евклид нигде в книге не ссылается на других греческих математиков, хотя несомненно опирается на их результаты. Историки науки [9] [10] показали, что прототипом для труда Евклида послужили более ранние сочинения античных математиков:
Манускрипты и издания «Начал»
Греческий текст «Начал»
Папирус из Оксиринха
При раскопках античных городов найдено несколько папирусов, содержащих небольшие фрагменты «Начал» Евклида. Самый известный был найден в «городе папирусов» Оксиринхе в 1896—1897 и содержит формулировку II prop. 5 с рисунком. [11]
Греческий текст «Начал» Евклида известен по византийским манускриптам, из них самые известные:
На их основе, а также с учётом арабских переводов «Начал» (IX век и далее) оригинальный текст был реконструирован датским историком науки Гейбергом в конце XIX века, его методы подробно описаны Хизом ( T. L. Heath ). [12]
Гейберг использовал в своей реконструкции 8 греческих манускриптов, датируемых сейчас IX—XI веками. Из этих манускриптов семь в своем заглавии имеют пометку «из издания Теона » или «из лекций Теона» и поэтому называются Теоновскими. Ватиканский манускрипт такой пометки не имеет и считается неподверженным редакции Теона. Теоновские манускрипты разнятся между собой, и общих признаков, отличающих их от ватиканского манускрипта, немного (наиболее существенный — концовка IV книги). На полях манускриптов имеются многочисленные комментарии, взятые частично из комментариев Прокла, которые вписывают «Начала» в контекст греческой культуры, напр., сообщается о том, что Пифагор, открыв свою теорему, принес в жертву быков.
История обретения византийских манускриптов темна. Вероятно, они попали в Европу ещё в XVI веке, но не были опубликованы. В первом издание греческого текста, осуществленном Йоханом Хервагеном (Johann Herwagen) между 1533 и 1558 под редакцией Симона Гринера (Simon Gryner, он же Grynaeus, профессор греческого в базельском университете), использованы манускрипты, которые, по мнению Гейберга, представляют собой весьма плохие копии XVI века. Лишь в 1808 Пейрар (F. Peyrard) во время наполеоновских экспроприаций нашел три манускрипта в Ватикане и среди них важнейший ватиканский.
Латинский текст «Начал»
Манускрипт из Люнебурга, ок. 1200 года, передающий геометрию Боэция.
Русские переводы
Первое издание «Начал» на русском языке произошло в 1739 году; книга вышла в Петербурге под названием «Евклидовы элементы из двенадцати нефтоновых книг выбранныя и в осьмь книг через профессора мафематики Андрея Фархварсона сокращенныя, с латинского на российский язык хирургусом Иваном Сатаровым преложенныя». [18] Перевод выполнил И. П. Сатаров под руководством шотландского математика Генри Фарварсона (Henry Fargwarson). [19] Имя Ньютона («Нефтона») в названии упомянуто, возможно, в рекламных целях, к содержанию книги он никакого отношения не имеет. Перевод был сделан с сокращённого французского издания «Начал» А. Такэ (A. Tacquet). [18] Немного позднее вышли ещё 2 перевода, также сокращённые до 8 книг:
Всемирное распространение
Тексты «Начал»
В сети доступны следующие манускрипты и печатные издания «Начал»:
«Начала» Евклида
«Начала» Евклида
— научное произведение, написанное в 3 в. до н. э., содержащее основы античной математики: элементарной геометрии, теории чисел, алгебры, общей теории отношений и метода определения площадей и объемов, включавшего элементы теории пределов. «Н.» Е.- образец дедуктивной системы, содержащей исходные предложения геометрии и других разделов математики, на основе к-рых все теории развиваются строго логически.