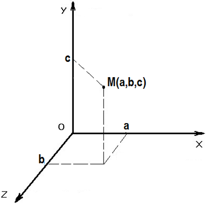
Что такое начальная координата в физике
Определение координаты движущегося тела (9 класс)
Как определить координаты движущегося тела? Для этого необходимо знать такие понятия, как механическое движение, пройденный путь, скорость, перемещение.
Механическое движение
При механическом движении происходит изменение положения тела в пространстве относительно других тел за промежуток времени. Оно бывает равномерным и неравномерным.
Равномерное движение
При равномерном движении тело за равные промежутки времени проходит одинаковые расстояния (т.е. движется с постоянной скоростью).
Путь, пройденный при равномерном движении равен: Sx=Vxt=x-xо
Следовательно, при равномерном движении координата тела изменяется по следующей зависимости:
Рис. 1. Формула координаты тела при прямолинейном равномерном движении
Неравномерное движение
Неравномерное движение – движение, при котором тело за равные промежутки времени проходит неодинаковые расстояния (движется с непостоянной скоростью), то есть движется с ускорением.
Если тело движется неравномерно, то скорость тела в разные моменты отличается не только по величине, но и (или) по направлению. Средняя скорость тела при неравномерном движении определяется по формуле: V (ср)= S (весь)/t (весь)
Ускорение – величина, показывающая, как изменяется скорость за 1 секунду.
Рис. 2. Формула ускорения
Следовательно, скорость в любой момент времени можно найти следующим образом:
V=Vо+at
Если скорость с течением времени увеличивается, то a больше 0, если скорость с течением времени уменьшается, то a меньше 0.
Как найти путь при равноускоренном движении?
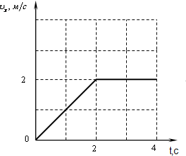
Рис. 3. Прямолинейное равноускоренное движение
Пройденный путь численно равен площади под графиком. То есть Sx=(Vox+Vx)t/2
Скорость в любой момент времени равна Vx=Vox+axt, следовательно Sx=Voxt+axt2/2
Так как перемещение тела равно разности конечной и начальной координат (Sx=X-Xo), то координата в любой момент времени вычисляется по формуле X=Xo+Sx, или
Движение тела по вертикали
Если тело движется по вертикали, а не по горизонтали, то такое движение всегда является равноускоренным. Когда тело падает вниз, то падает оно всегда с одинаковым ускорением – ускорением свободного падения. Оно всегда одинаковое: g=9,8 м/кв.с.
При движении по вертикали формула скорости приобретает вид: Vy=Voy+gt,
где Vy и Voy – проекции начальной и конечной скоростей на ось OY.
Координату же можно рассчитать по формуле: Y=Yo+Voyt+gt2/2
Движение тела по окружности
При движении по окружности численное значение скорости может и не изменяться, но поскольку обязательно изменяется направление, то движение по окружности – это всегда равноускоренное движение.
Что мы узнали?
Тема «Определение координаты движущего тела», которую изучают в 9 классе, поможет ученикам систематизировать информацию о том, что движение может быть равномерным и неравномерным. Так же для того чтобы знать пройденный путь, нужно выбрать тело отсчета и использовать прибор для отсчета времени.
Механическое движение и его характеристики
теория по физике 🧲 кинематика
Механика — раздел физики, который изучает механическое движение физических тел и взаимодействие между ними.
Основная задача механики — определение положение тела в пространстве в любой момент времени.
Механическое движение — изменение положения тела в пространстве относительно других тел с течением времени.
Механическое движение и его виды
По характеру движения точек тела выделяют три вида механического движения:
По типу линии, вдоль которой движется тело, выделяют два вида движения:
По скорости выделяют два вида движения:
По ускорению выделяют три вида движения:
Что нужно для описания механического движения?
Для описания механического движения нужно выбрать, относительно какого тела оно будет рассматриваться. Движение одного и того же объекта относительно разных тел неодинаковое. К примеру, идущий человек относительно дерева движется с некоторой скоростью. Но относительно сумки, которую он держит в руках, он находится в состоянии покоя, так как расстояние между ними с течением времени не изменяется.
Решение основной задачи механики — определения положения тела в пространстве в любой момент времени — заключается в вычислении координат его точек. Чтобы вычислить координаты тела, нужно ввести систему координат и связать с ней тело отсчета. Также понадобится прибор для измерения времени. Все это вместе составляет систему отсчета.
Система отсчета — совокупность тела отсчета и связанных с ним системы координат и часов.
Тело отсчета — тело, относительно которого рассматривается движение.
Часы — прибор для отсчета времени. Время измеряется в секундах (с).
При описании движения тела важно учитывать его размеры, так как характер движения его отдельных точек может различаться. Но в рамках некоторых задач размер тела не влияет на результат решения. Тогда его можно считать пренебрежительно малым. Тогда тело рассматривают как движущуюся материальную точку.
Материальная точка — это тело, размерами которого можно пренебречь в условиях конкретной задачи. Допустимо принимать тело за точку, если оно движется поступательно или его размеры намного меньше расстояний, которые оно проходит.
Виды систем координат
В зависимости от характера движения тела для его описания выбирают одну из трех систем координат:
Способы описания механического движения
Описать механическое движение можно двумя способами:
Координатный способ
Указать положение материальной точки в пространстве можно, используя трехмерную систему координат. Если эта точка движется, то ее координаты с течением времени меняются. Так как координаты точки зависят от времени, можно считать, что они являются функциями времени. Математически это записывается так:
Эти уравнения называют кинематическими уравнениями движения точки, записанными в координатной форме.
Векторный способ
Радиус-вектор точки — вектор, начало которого совпадает с началом системы координат, а конец — с положением этой точки.
Указать положение точки в трехмерном пространстве также можно с помощью радиус-вектора. При движении точки радиус-вектор со временем изменяется. Он может менять направление и длину. Это значит, что радиус-вектор тоже можно принять за функцию времени. Математически это записывается так:
Эта формула называется кинематическим уравнением движения точки, записанным в векторной форме.
Характеристики механического движения
Движение материальной точки характеризуют три физические величины:
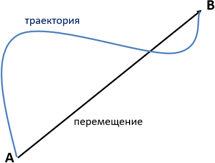
Перемещение
Траектория — линия, которую описывает тело во время движения.
Путь — длина траектории. Обозначается буквой s. Единица измерения — метры (м).
Путь есть функция времени:
Модуль перемещения — длина вектора перемещения. Обозначается как |Δ r |. Единица измерения — метры (м).
Модуль перемещения необязательно должен совпадать с длиной пути.
Пример №1. Человек обошел круглое поле диаметром 1 км. Чему равны пройденный путь и перемещение, которое он совершил.
Путь равен длине окружности. Поэтому:
Человек, обойдя круглое поле, вернулся в ту же точку. Поэтому его начальное положение совпадает с конечным. В этом случае человек совершил перемещение, равное нулю.
Пример №2. Точка движется по окружности радиусом 10 м. Чему равен путь, пройденный этой точкой, в момент, когда модуль перемещения равен диаметру окружности?
Диаметр — это отрезок, который соединяет две точки окружности и проходит через центр. Перемещение равно длине этого отрезка в случае, если один из концов этого отрезка является началом вектора перемещения, а другой — его концом. Траекторией движения в этом случае является дуга, равная половине окружности. А длина траектории есть путь:
Скорость
Скорость — векторная физическая величина, характеризующая быстроту перемещения тела. Численно она равна отношению перемещения за малый промежуток времени к величине этого промежутка.
Скорость характеризуется не только направлением вектора скорости, но и его модулем.
Модуль скорости — расстояние, пройденное точкой за единицу времени. Обозначается буквой V и измеряется в метрах в секунду (м/с).
Математическое определение модуля скорости:
Величина скорости тела в данный момент времени есть первая производная от пройденного пути по времени:
Ускорение
Ускорение — векторная физическая величина, которая характеризует быстроту изменения скорости тела. Численно она равна отношению изменения скорости за малый промежуток времени к величине этого промежутка.
Модуль ускорения — численное изменение скорости в единицу времени. Обозначается буквой a. Единица измерения — метры в секунду в квадрате (м/с 2 ).
Математическое определение модуля скорости:

Ускорение тела есть первая производная от скорости или вторая производная от пройденного пути по времени:
Проекция вектора перемещения на ось координат
Проекция вектора перемещения на ось — это скалярная величина, численно равная разности конечной и начальной координат.
Проекция вектора на ось OX:
Проекция вектора на ось OY:
Знаки проекций перемещения
Проекция вектора перемещения на ось считается нулевой, если вектор расположен перпендикулярно этой оси.
Модуль перемещения — длина вектора перемещения:
Модуль перемещения измеряется в метрах (м).
Вместе с собственными проекциями модуль перемещения образует прямоугольный треугольник. Сам он является гипотенузой этого треугольника. Поэтому для его вычисления можно применить теорему Пифагора. Выглядит это так:
Выразив проекции вектора перемещения через координаты, эта формула примет вид:
Выражение проекций вектора перемещения через угол его наклона по отношению к координатным осям:
Общий вид уравнений координат:
Пример №3. Определить проекции вектора перемещения на ось OX, OY и вычислить его модуль.
Определяем координаты начальной точки вектора:
Определяем координаты конечной точки вектора:
Проекция вектора перемещения на ось OX:
Проекция вектора перемещения на ось OY:
Применяем формулу для вычисления модуля вектора перемещения:
Пример №4. Определить координаты конечной точки B вектора перемещения, если начальная точка A имеет координаты (–5;5). Учесть, что проекция перемещения на OX равна 10, а проекция перемещения на OY равна 5.
Извлекаем известные данные:
Для определения координаты точки В понадобятся формулы:
Выразим из них координаты конечного положения точки:
Точка В имеет координаты (5; 10).
Алгоритм решения
Решение
Записываем исходные данные:
Записываем формулу ускорения:
Так как начальная скорость равна 0, эта формула принимает вид :
Отсюда скорость равна:
Подставляем имеющиеся данные и вычисляем:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Что такое начальная координата в физике
10 класс
Материалы к зачету по теме «Основные законы механики «
1. Механическое движение.
Явление механического движения тел (материальных точек)состоит в том, что положение тела относительно других тел, т. е. его координаты, с течением времени изменяется.Чтобы найти координаты тела в любой момент времени, нужно знать начальные координаты и вектор перемещения тела. Изменение координаты тела равно проекции вектора перемещения на соответствующую ось координат.
Прямолинейное равномерное движение — это самый простой вид движения.При таком движении нужно определять лишь одну координату потому, что координатную ось можно направить вдоль направления движения тела. Координату х тела (материальной точки) в любой момент времени t можно вычислить по формуле:
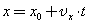
где 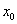
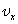
Механическое движение относительно. Это значит, что перемещение и скорость тела относительно различных систем координат, движущихся друг относительно друга, различны.
Покой также относителен. Если относительно какой-то системы координат тело покоится, то существуют и такие системы отсчета, относительно которых оно движется.
2. Основная задача механики
состоит в нахождении положения тела в любой момент времени. Решение этой задачи идет по своеобразной «цепочке»:
чтобы найти координату точки, нужно знать ее перемещение, а чтобы вычислить перемещение, нужно знать скорость движения.
По такой цепочке: скорость → перемещение → координата решают задачи механики для прямолинейного равномерного движения.
Если движение ускоренное, то нужно знать ускорение, так что при таком движении задачи решают по «цепочке» ускорение → скорость → перемещение → координата. И для равномерного, и для ускоренного движения должны быть известны начальные условия — начальные координаты и начальная скорость.
При прямолинейном ускоренном движении мгновенная скорость тела (материальной точки) непрерывно изменяется от одного момента времени к другому. Поэтому для вычисления скорости в любой момент времени и в любой точке нужно знать быстроту ее изменения, т.е. ускорение:
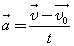
Проекцию скорости тела на выбранную координатную ось в любой момент времени t вычисляют по формуле:
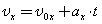
Координату тела находят по формуле:
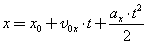
Проекцию перемещения находят по формуле:
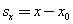
Из приведенных формул получаются формулы для скорости, координат и перемещений при равномерном прямолинейном движении, если принять, что а x = 0.
Значение проекции перемещения при равноускоренном движении можно определить также по формуле:
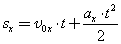
| Так как | 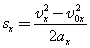 | , то для координаты тела х имеем: | 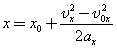 |
При вычислениях по приведенным формулам знаки проекций векторов 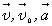
3. При криволинейном движении непрерывно изменяется направление вектора скорости, и в каждой точке траектории он направлен по касательной к траектории в данной точке. Поэтому даже равномерное движение по криволинейной траектории, при котором значение модуля скорости постоянно, есть ускоренное движение. Движение тела (материальной точки) по окружности описывают не только с помощью линейных величин — перемещения и скорости, но и с помощью угловых величин — угла поворота радиуса φ, проведенного из центра окружности к телу, и угловой скорости ω.
Связь между линейной и угловой скоростью выражается формулой:
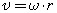
где r — радиус окружности.
При равномерном движении по окружности вектор ускорения в любой точке окружности перпендикулярен вектору скорости и направлен к центру окружности. Модуль вектора центростремительного ускорения выражается равенством:
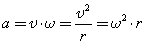
Относительно вращающегося стержня (оси) не закрепленное на нем тело (точка) движется вдоль стержня по направлению от оси вращения.
Пример решения задачи:
1. Ширина реки 200 м. Лодка, держа курс перпендикулярно течению реки, достигла противоположного берега за 140 с. Скорость течения воды в реке 0,8 м/с. Определите скорость и перемещение лодки относительно берега.
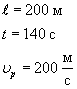  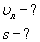 | 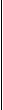 | 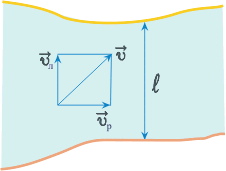 |
Ответ: Скорость лодки относительно берега 1,6 м/с, перемещение 112 м.
Решите задачи самостоятельно:
1. Через реку переправляется лодка, выдерживая курс перпендикулярно течению. Скорость лодки
4 м/с, скорость течения реки 3 м/с. Какова ширина реки, если лодку снесло на 60 м?
3. Автомобиль движется: а) с постоянной скоростью; б) с постоянным ускорением;
в) с положительным ускорением; г) с отрицательным ускорением.
Назовите вид каждого движения и изобразите соответствующие графики скорости.
17. Механика  Читать 0 мин.
Читать 0 мин.
17.20. Движение
Движением тела называется изменение его положения в пространстве относительно других.
Координата— величина, служащая для определения положения какой-либо точки на плоскости или в пространстве.
Перемещением тела называется вектор, соединяющий начальное положение тела с его последующим положением.
Траектория — это линия, вдоль которой движется тело.
Путь — это длина траектории, вдоль которой движется тело.
Прямолинейным равномерным движением называется движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения.
Скорость ― это векторная величина!
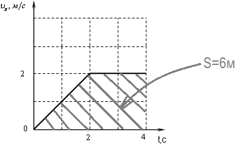
В заданиях, где дана зависимость скорости тела от времени,
пройденный путь можно вычислить как площадь под графиком:
Ускорением тела называется векторная величина, равная отношению изменения скорости за любой промежуток времени к величине этого промежутка:
Зависимость скорости от времени при наличии ускорения определяется выражением:
$\overrightarrow
Равноускоренным движением тела называется движение, при котором его ускорение не меняется, ни по величине, ни по направлению.
Уравнение равноускоренного движения в проекции на ось х имеет вид:
Применение производной в кинематике
Если существует зависимость координаты от времени x(t), то зависимость скорости от времени можно получить, взяв производную по времени от этой зависимости.
Скорость ― это производная координаты тела по времени:
Например, если зависимость координаты тела при равноускоренном движении имеет вид
то взяв первую производную от координаты, мы получим зависимость скорости тела от времени:
Точно также, ускорение ― это производная от скорости тела:










































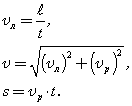
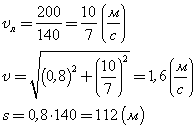
 Читать 0 мин.
Читать 0 мин.