Что такое наглядное изображение в черчении

Что такое наглядное изображение в черчении

Предметы, которые мы видим: сооружения, машины, механизмы, детали — можно изображать на плоскости разными способами. Одним из этих способов является рисование. При рисовании предмет изображается от руки так, как это воспринимается нашим зрением или воображением. Рисунок передает форму предмета и его отдельные части с искажением, например, деталь на рис. 81. По этому рисунку мы не можем получить точное представление о формах и размерах отверстий и отдельных элементах детали. Все круглые отверстия изображаются овалами. Поэтому такой передачей формы и размеров изделия пользуются в технике только для вспомогательных изображений.

В отличие от рисунка чертеж может передавать форму предмета не одним, а несколькими изображениями (проекциями, видами). При этом каждая отдельная проекция (вид) на чертеже изображает только одну сторону предмета. Такой вид изображения помогает точно установить формы и размеры будущего изделия.

Чертежи должны выполняться по методу прямоугольного проецирования и с соблюдением ряда правил.

Рассмотрим существующие методы проецирования.

Способы изображения пространственных форм на плоскости рассматриваются и изучаются в предмете, который называется начертательной геометрией.

На основах начертательной геометрии базируется проекционное черчение, которое является основой машиностроительного черчения. В проекционном черчении изучаются практические приемы изображения геометрических тел и их сочетаний.

Любую сложную форму детали машин можно представить как совокупность простейших геометрических тел или их частей. Поверхности деталей машин представляют собой плоскости и другие поверхности, чаще всего поверхности вращения (цилиндрическая, коническая, сферическая, торовая, винтовая). Пример детали, ограниченной такими простейшими геометрическими поверхностями, показан на рис. 81.

Изображение на плоскости предмета, расположенного в пространстве, полученное при помощи прямых линий — лучей, проведенных через каждую характерную точку предмета до пересечения этих лучей с плоскостью, называется проекцией этого предмета на данную плоскость.

Точки пересечения лучей с плоскостью называются проекциями точек предмета, а плоскость, на которую проецируются точки, плоскостью проекций.

Если все лучи, называемые проецирующими прямыми, проводятся из одной точки (центра) О, то полученное на плоскости проекций изображение предмета называется его центральной проекцией.

Центральная проекция предмета получается следующим образом: из точки схода лучей О (рис. 82, а), называемой центром проекций, проводят ряд проецирующих лучей через все наиболее характерные точки предмета до пересечения с плоскостью проекций V.

В результате получим изображение предмета, называемое его проекцией. Это изображение получается увеличенным — размеры изображения не соответствуют действительным размерам предмета — и дает представление только о форме предмета, а не о его размерах. Поэтому центральные проекции в машиностроительных чертежах почти не применяются.

Аксонометрическая проекция предмета получается, если точку схода лучей (центр проецирования) мысленно перенести в бесконечность (отодвинуть от плоскости проекций бесконечно далеко).

При построении аксонометрической проекции предмет также помещается перед плоскостью проекций V, проецируют предмет вместе с осями и на эту плоскость. Проецирующие лучи проводят параллельно друг другу (рис. 82, б).

Аксонометрические проекции дают наглядное, но искаженное изображение предмета: прямые углы преобразуются в острые и тупые, окружности — в эллипсы и т. д. В технике аксонометрические проекции применяются только в тех случаях, когда требуется выполнить наглядное изображение.

Прямоугольные (ортогональные) проекции. Здесь центр проекции также удален от плоскости проекций бесконечно далеко, проецирующие лучи параллельны и составляют с плоскостью проекций прямой угол (отсюда и название — прямоугольные проекции).

Производственные чертежи выполняют в прямоугольных проекциях. Предмет располагают перед плоскостью проекций так, чтобы большинство его линий и плоских поверхностей были параллельны этой плоскости (рис. 82, в). Тогда эти линии и поверхности будут изображаться на плоскости проекций в действительном виде.

Изображение на одну плоскость V в общем случае не дает представления об объеме предмета, поэтому прямоугольные проекции выполняют не на одной плоскости проекций, а на двух (плоскости или трех взаимно перпендикулярных плоскостях. По такому чертежу можно представить себе форму предмета и найти размеры всех элементов.

Проекция с числовыми отметками. В некоторых случаях применяют проекции с числовыми отметками, которые представляют собой прямоугольную (ортогональную) проекцию предмета на горизонтальную плоскость проекций, называемую плоскостью нулевого уровня. Расстояние каждой точки изображаемого объекта от плоскости уровня указывается числовой отметкой.

При этом используется только горизонтальная плоскость проекций. Например, на рис. 83, б показан топографический план, который изображает возвышенность (рис. 83, а).

Для построения профиля поверхности этой возвышенности все линии пересечения топографической поверхности с горизонталями переносят на чертеж.

Точки с одинаковым расстоянием от нулевого уровня образуют непрерывную линию, в разрыве которой ставится число, равное расстоянию до нулевого уровня.

Источник

86. Построение наглядного изображения предмета

Для построения наглядного изображения предмета воспользуемся аксонометрическими проекциями (гл. 12). Выполнить его можно по его комплексному чертежу. Воспользовавшись рис. 172, построим

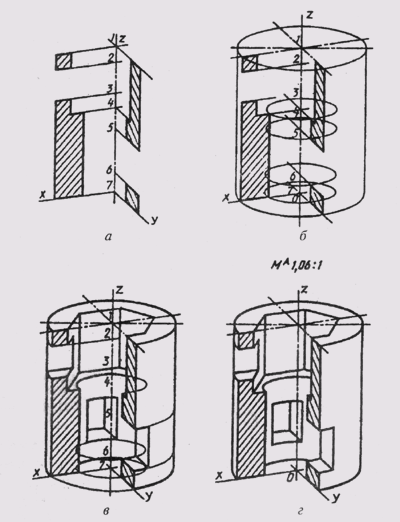
стандартную прямоугольную изометрию изображенного на нем предмета. Воспользуемся приведенными коэффициентами искажения. Примем расположение начала координат (точка О) — в центре нижнего основания предмета (рис. 198). Вычертив оси изометрии и установив масштаб изображения (М А 1,22 : 1), отмечаем центры окружностей верхнего и нижнего оснований цилиндра, а также окружностей, ограничивающих Т-образный вырез. Вычерчиваем эллипсы, являющиеся изометрией окружностей (см. § 77). Затем проводим линии, параллельные координатным осям, которые ограничивают вырез в цилиндре. Изометрию линии пересечения сквозного цилиндрического отверстия, ось которого

параллельна оси Оу с поверхностью основного цилиндра, строим по отдельным точкам, используя те же точки (К, L, М и им симметричные), что и при построении вида слева. Затем удаляем вспомогательные линии и обводим окончательно изображение с учетом видимости отдельных частей предмета.

Плоские фигуры, получаемые при этом, уже построены на комплексном чертеже, так как они являются половинами фронтального и профильного разреза предметов (рис. 185, б).

Построение наглядного изображения начинаем с проведения осей диметрии и указания масштаба М А 1,06 : 1 (см. § 78). На оси z отмечаем положение центров 1, 2. 7 (рис. 199, а); расстояния между ними берем с главного вида предмета. Через отмеченные точки проводим оси диметрии. Затем строим в диметрии фигуры сечения сначала в плоскости xOz, а затем в плоскости yOz. Размеры координатных отрезков берем с комплексного чертежа (рис. 185); при этом размеры по оси у сокращаем в два раза. Выполняем штриховку сечений. Угол наклона линий штриховки в аксонометрии определяется диагоналями параллелограммов, построенных на аксонометрических осях с учетом коэффициентов искажения. На рис. 200, а приведен пример выбора направления штриховки в изометрии, а на рис. 200, б — в диметрии. Далее строим эллипсы — диметрию окружностей, расположенных в горизонтальных плоскостях (см. рис. 199, б). Проводим контурные линии наружного цилиндра, внутренних вертикальных отверстий, строим основание этих отверстий (рис. 199, в); вычерчиваем видимые линии пересечения горизонтальных отверстий с наружной и внутренними поверхностями.

Затем удаляем вспомогательные линии построения, проверяем правильность выполнения чертежа и обводим чертеж линиями требуемой толщины (рис. 199, г).

Источник

Понятие об аксонометрических проекциях

Наглядные изображения применяют для пояснения чертежей деталей и машин. По ним легче представить форму предмета, чем по чертежу в трёх видах.

Одним из видов наглядных изображений являются аксонометрические изображения.

Аксонометрия в переводе с греческого означает «измерение по осям».

Аксонометрические проекции получают путём проецирования параллельными лучами

предмета, который связан с осями прямоугольных координат, на некоторую плоскость Р (рис. 103).

Таким образом, аксонометрическая проекция – это проекция только на одну плоскость.

Чтобы изображение получилось наглядным, проецирующие лучи не должны быть параллельны ни одной оси координат. Тогда на плоскости Р будут, хоть и с искажениями, изображены все три измерения предмета.

Аксонометрические проекции в зависимости от направления проецирования делятся на два вида: прямоугольные, когда направление проецирования перпендикулярно плоскости Р (угол φ=90°), и косоугольные, когда угол φ≠90°.

Если плоскость Р не параллельна ни одной из координатных плоскостей x,y,z, то на аксонометрической проекции у предмета искажаются все три его измерения. Если же плоскость Р параллельна одной или двум осям координат, то у предмета искажаются размеры соответственно по двум его измерениям или по одному.

Величина искажения определяется коэффициентом искажения, который равен отношению длины аксонометрической проекции отрезка, параллельного соответствующей оси координат, к его действительной длине. Любая аксонометрическая проекция имеет три коэффициента искажения по числу осей координат.

В зависимости от того, разные они или одинаковые, аксонометрические проекции делят на изометрические (коэффициенты искажения равны по всем трём осям) и триметрические (коэффициенты искажения по всем осям разные).

Стандартные виды аксонометрии. Изометрия. Диметрия

Наиболее распространёнными видами аксонометрических проекций являются прямоугольная изометрическая проекция (изометрия) и прямоугольная диметрическая проекция (диметрия), основные правила построения которых определены стандартом.

Прямоугольная изометрия представляет собой аксонометрическую проекцию с направлением проецирования, перпендикулярным к плоскости аксонометрических проекций одинаковыми по всем трём осям коэффициентами искажения, равными 0,82.

Оси изометрии (рис. 104а) составляют между собой углы 120°. Ось Z расположена вертикально. Для упрощения построения коэффициент искажения принимают равным 1.

Изображение при этом получается увеличенным, но вид его не меняется, т.к. сохраняется пропорциональность всех его размеров.

На рис. 104б и в приведены два способа построения осей в изометрии.

Прямоугольная диметрия представляет собой аксонометрическую проекцию с направлением проецирования, перпендикулярным аксонометрической плоскости проекций Р и одинаковыми коэффициентами искажения по осям х и z.

Ось х (рис. 105а) составляет с горизонтальной прямой угол 7°10′, а ось у – угол 41°25′.

Ось z занимает вертикальное положение. На рис. 105б показан графический способ построения осей диметрии.

В диметрии коэффициенты искажения по осям х и z равны 0,94, а по оси у – 0,47. При построениях первый коэффициент округляют до 1, а второй – до 0,5. Таким образом, отрезки, параллельные осям координат х и z, откладывают в натуральную величину, а длину отрезков, параллельных оси у, уменьшают в два раза.

Построение окружности в аксонометрии

Изометрия. Изометрические проекции окружностей, расположенных в плоскостях проекций или в плоскостях, им параллельных, есть эллипсы (рис. 106).

Большие оси этих эллипсов равны l,22Dокр, а малые 0,71Dокр, где Dокр – диаметр изображаемой окружности. Большая ось эллипсов всегда перпендикулярна к той аксонометрической оси, которая отсутствует в плоскости окружности, а малая совпадает с этой осью или параллельна ей.

Практически при построении изометрии окружности эллипс обычно заменяют близким к нему по форме овалом, т.к. построение овала значительно проще.

Наиболее простой способ построения овала показан на рис. 107.

На рис. 108а,б построены изометрии окружностей, расположенных во фронтальной и профильной плоскостях.

Окружности, расположенные во фронтальной плоскости, проецируются в виде эллипсов с большой осью, равной 1,06Dокр, а малой – 0,94Dокр. Большие оси эллипсов, как и в изометрии, перпендикулярны к той аксонометрической оси, которая отсутствует в данной плоскости, а малые оси совпадают с направлением этой оси.

Диметрии окружностей (эллипсы) обычно заменяют овалами, размеры осей которых равны размерам соответствующих осей эллипсов. Построение этих овалов показано на рис. 110. На рис. 110а построения понятны по чертежу.

На рис. 110б строим оси диметрии х_р, у_р, z_р. Затем строим прямую, перпендикулярную оси у_р. Отложив на осях х_р и z_р радиус заданной окружности, получим точки М, К, N, L, которые являются точками сопряжения дуг овала. Через точки М и N проводим горизонтальные прямые. В пересечении этих прямых с осью у_р и перпендикуляром к ней получим точки О₁, О₂, О₃, О₄. Из центров O₁ и О₃ опишем дуги радиусом R₁=О₃ K, а из центров О₂ и О₄ – дуги радиусом R₂=О₂M.

Аксонометрические изображения предметов

Приступая к построению аксонометрической проекции предмета, следует выбрать вид аксонометрии, обеспечивающий наибольшую наглядность изображения. Затем предмет связывают с системой прямоугольных координат, оси которой обычно совмещают с осями симметрии предмета. Только после этого можно приступить к построению аксонометрии.

Построение аксонометрии предмета обычно начинают с построения аксонометрии одной из его проекций (вторичной проекции). Затем полученное изображение дополняют построением третьего измерения всех его точек.

На рис. 111 показан пример построения прямоугольной изометрии предмета через построение его горизонтальной проекции.

На рис. 112 приведен пример построения прямоугольной изометрии детали путём построения её вторичной фронтальной проекции.

Для выявления внутренней формы предмета, изображённого в аксонометрии, в некоторых случаях применяют разрезы, которые условно называют вырезами. При этом используют две секущие плоскости, обычно совпадающие с плоскостями симметрии предмета (рис. 113).

рис. 111 рис. 112 рис. 113

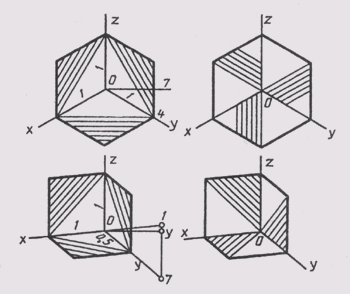
Линии штриховки сечений в аксонометрических проекциях наносят параллельно одной из диагоналей проекций квадратов, лежащих в соответствующих координатных плоскостях. Стороны квадратов параллельны аксонометрическим осям (рис. 114).

Источник

Что такое наглядное изображение в черчении

При построении комплексного чертежа изображаемый предмет обычно располагают так, чтобы направления трех главных измерений (длина — высота — ширина — были бы параллельны координатным осям плоскостей проекций (рис. 2.31, а). Обычно . В этом случае на каждой из проекций два измерения проецируются в натуральную величину без искажения, но третье измерение проецируется в точку, т. е. отсутствует. Поэтому для полного представления о форме предмета необходимы еще одна или несколько проекций на другие плоскости проекций. Несколькими проекциями можно добиться полной информативности комплексного чертежа о форме предмета. Однако на таком чертеже теряется одно из основных качеств изображения, а именно наглядность. Представить истинную пространственную форму предмета по такому чертежу бывает достаточно трудно, особенно для предметов сложной геометрической формы.

Для того чтобы чертеж стал наглядным, необходимо построить проекцию предмета, на которой ни одно из главных измерений не проецировалось бы в точку. Для этого предмет следует соответствующим образом расположить перед плоскостями проекций, чтобы он был виден сразу с трех сторон: спереди, сверху и слева (рис. 2.31, б).

Наглядные изображения могут быть выполнены в свободной манере с приближенным соблюдением соотношений размеров по осям, а могут быть построены по определенным законам. В наглядных изображениях искажаются углы между координатными осями (рис. 2.31, е) и линейные размеры по этим осям. Отношение длины проекции отрезка, параллельного координатной оси, к его истинной длине определяет коэффициент искажения размера по этой оси: — коэффициент искажения вдоль оси х; — то же вдоль оси то же вдоль оси Наглядные изображения, построенные с заданными коэффициентами искажения по главным измерениям и углами между координатными осями, называют аксонометрическими роекциями.

Для прямоугольных аксонометрических проекций существует зависимость между коэффициентами искажения

Правила построения стандартных аксонометрических проекций устанавливает ГОСТ 2.317-69. Наибольшее применение на практике имеют следующие аксонометрические проекции: изометрическая и днметрическая прямоугольные проекции, косоугольная фронтальная диметрическая проекция (рис. 2.32).

Рис. 2.31. Построение наглядного изображения. а — комплексный чертеж; наглядное изображение; в — расположение координатных осей

Изометрическая прямоугольная проекция предполагает, что коэффициенты искажения по всем трем осям одинаковы:

и в соответствии с вышепрннятой формулой равны 0,82. Углы между координатными осями также одинаковы, и равны (рис. 2.33,а). Как правило, при построении изображения предмета в изометрической проекции в целях упрощения используют приведенный коэффициент искажения -Изображение в этом случае получается несколько увеличенным, как бы построенным в масштабе

Диметрическая прямоугольная проекция предполагает одинаковыми коэффициенты искажения по двум осям. В стандартной форме диметрической прямоугольной проекции приняты одинаковыми коэффициенты искажения по осям и 2, а по оси у — в 2 раза меньший, т.е. Действительные коэффициенты искажения равны В целях упрощения построения диметрическую проекцию выполняют без искажения по осям и с коэффициентом искажения по оси Положение координатных осей для днметрической прямоугольной проекции приведено на рис.

Косоугольная фронтальная диметрическая проекция имеет те же коэффициенты искажения, что и прямоугольная диметрическая проекция, но выгодно отличается от нее более удобным расположением координатных осей, что упрощает геометрические построения.

Из других косоугольных аксонометрических проекций, которые рекомендует следует назвать изометрические фронтальную и горизонтальную проекции, каждая из которых выполняется без искажения по всем трем осям: (Подробнее об этих проекциях см.

Необходимо остановиться на построении проекций окружностей в аксонометрии. Как правило, проекциями окружностей являются эллипсы (рис. 2.34). Исключение составляет косоугольная фронтальная диметрическая проекция окружности, лежащей в плоскости, параллельной фронтальной плоскости. Эта проекция представляет собой заданную окружность без искажений. Параметры эллипсов, представляющих собой проекции окружностей, лежащих в координатных плоскостях, приведены

Рис. 2.33. Положение аксонометрических осей: а — изометрии; днметрии; в — косоугольная фронтальная диметрня

Рис. 2.34. Аксонометрические проекции окружностей

в табл. 2.3. Следует заметить, что размеры диаметров эллипсов, параллельных координатным осям, равны диаметрам заданных окружностей.

Чаще всего аксонометрические проекции применяются для построения наглядных изображений деталей. Но возможны случаи, когда в целях усиления наглядности изображение сборочной единицы строится в аксонометрической проекции (рис. 2.35).

Для показа внутренних форм предмета в аксонометрических проекциях используют разрезы. Чаще всего плоскости разреза совпадают с главными плоскостями симметрии (рис. 2.35). В аксонометрических проекциях, как правило, не применяют полных разрезов, не пользуются теми условностями, которые применяют в комплексных чертежах. Линии штриховки сечений наносят параллельно диагоналям квадратов, лежащих в соответствующих плоскостях проекций. При нанесении размеров выносные линии проводят параллельно аксонометрическим осям, размерные линии — параллельно измеряемому отрезку.

Аксонометрические изображения являются самыми простыми из наглядных изображений, применяемых в технике, и используются достаточно широко. Но метод параллельного проецирования, который используется при построении аксонометрических проекций, не позволяет строить изображения предметов такими, как мы их видим в действительности. Метод параллельного проецирования не учитывает следующие основные законы зрения человека:

1) равные между собой расстояния при удалении от наблюдателя, кажутся уменьшающимися;

2) параллельные линии сходятся в одной точке.

Построить изображение предметов с учетом этих зрительных законов можно, использовав метод центрального проецирования, при котором все проецирующие прямые

Таблица 2.3. (см. скан) Окружности в аксонометрических проекциях

Рис. 2.35. (см. скан) Разрезы в аксонометрии

пересекаются в одной точке, называемой центром проецирования.

Сущность метода центрального проецирования представлена на рис. 2.36. Проецирующие прямые выходят из центра проецирования Изображение предмета строится на плоскости К, которая носит название картинной плоскости. Изображение предмета, построенное по методу центрального проецирования с учетом отмеченных выше законов зрения, носит название перспективного изображения, или, просто, перспективы. Часто перспективой называют метод построения изображений на картинной плоскости в соответствии с теми кажущимися сокращениями размеров и изменениями очертаний формы, которые наблюдаются в действительности.

Чтобы построить перспективу предмета, необходимо иметь две его проекции (рис. 2.37, а,б). На горизонтальной проекции (рис. 2.37,б) выбирается положение центра

Рис. 2.36. Метод центрального проецирования

проецирования и положение картинной плоскости К. Наиболее выразительным и естественным перспективное изображение бывает, если угол зрения а выбирается в пределах На фронтальной проекции (рис. 2.37,а) намечается высота линии горизонта Из центра проецирования проводим через характерные точки горизонтальной проекции проецирующие прямые и определяем проекции этих характерных точек на картинной плоскости. Далее находим точки схода параллельных прямых поперечного и продольного направлений, проводя из точки прямые, параллельные соответствующим сторонам предмета на горизонтальной проекции. Полученные точки используются при построении перспективы предмета (рис. 2.37, в). От положения картинной плоскости и линии горизонта зависит видимая форма предмета.

Сравнение различных изображений однбго и гого же предмета комплексного чертежа (см. рис. 2.21, 2.25), аксонометрических проекций (см. рис. 2.32) и перспективы (рис. 2.37) говорит о преимуществах и недостатках того или иного изображения. Комплексный чертеж дает полную информацию о форме и размерах предмета, однако изображение не является наглядным. Перспективное изображение является наиболее натуральным из всех видов изображений, но размеры предмета на

Рис. 2.38. (см. скан) Перспектива тепловой электростанции

Рис. 2.39. (см. скан) Перспектива здания приборостроительного завода

чертеже являются искаженными. Аксонометрические наглядные изображения являются более простыми для построения, чем перспективные изображения.

Наиболее широко перспектива используется в строительных и архитектурных чертежах, где изображаемые предметы имеют значительную протяженность в пространстве и изображение зданнй и сооружений на чертежах должно соответствовать восприятию их глазом человека.

Иллюстративный материал архитектурно-строительной документации включает в себя чертежи, в которых изображения, построенные в линейной графике, дополняются передачей светотени, фактуры материалов здания (рис. 2.38, 2.39). Для усиления

Рис. 2.40. (см. скан) Перспектива здания научно-исследовательского института

реальности изображения здания дополняются окружающими их предметами: соседней застройкой, растительностью, людьми и т. д. (рис. 2.40).

Источник