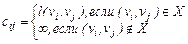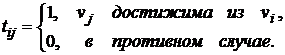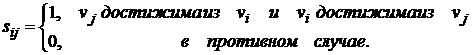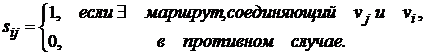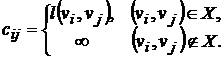Что такое нагруженный граф

Нагруженный граф. Пути в графе. Нахождение минимального пути в графах.

Нагруженный граф – орграф G = (V, X), для которого задана функция ставящая в соответствие каждой дуге этого графа некоторое вещественное число – длина (вес) дуги x l(x). Можно задать с помощью матрицы весов:

Замкнутый путь – путь (маршрут), у которого первая и последняя вершины совпадают. Замкнутый путь, который проходит через каждую дугу (ребро) только 1 раз называется циклом. Цикл, который проходит через каждую вершину 1 раз называется простым.

Цепь – незамкнутый путь (маршрут), который проходит через каждую дугу(ребро) только 1 раз. Цепь, которая проходит через каждую вершину 1 раз называется простой.

Длина пути (для ненагруженного графа) – количество дуг, входящих в этот путь.

Длина пути (для нагруженного графа) – сумма весов дуг, входящих в этот путь. Минимальный путь [между вершинами v₁ и v_k] – путь, имеющий минимальную длину среди всех других путей [из v₁ в v_k].

Алгоритм Дейкстры (поисл min пути в нагруженном графе)

1. Положим l*(s) = 0 и будем считать эту метку постоянной. Для всех v ОV, v № s, положим l*(v) = Ґ и будем считать эти метки временными. Положим p = s.

2. Для всех vОГp с временными метками выполним: если l*(v)>l*(p)+l(p,v), то l*(v)=l*(p)+l(p,v) и Q(v) =р. Иначе l*(v) и Q(v) не менять, т.е. l*(v) = min (l*(t), l*(p)+cpv). (Идея состоит в следующем: пусть p – вершина, получившая постоянную метку l*(p) на предыдущей итерации. Просматриваем все вершины vОГp, имеющие временные метки. Метка l*(v) вершины vОГp заменяется на l*(p)+l(p,v), если оказывается, что ее метка l*(v)>l*(p)+l(p,v). В этом случае говорим, что вершина v получила свою метку из вершины p, поэтому положим Q(v) = p. С помощью этих дополнительных меток будем потом восстанавливать сам путь. Если l*(v) Ј l*(p)+cpv, то метки остаются прежними.

4. Положим p = v*. Если p = t, то перейдем к п.5 ( l*(t) – длина минимального пути ). Иначе перейдем к п.2.

5. Найдем минимальный путь из s в t, используя метки Q(v): П = s…Q(t)t.

Источник

1.8. Нагруженные графы

Нагруженный граф − ориентированный граф D=(V,X), на множестве дуг которого определена некоторая функция , которую называют весовой функцией.

Цифра над дугой (см. рис. 5)− вес дуги (цена дуги).

Обозначения: для любого пути П нагруженного ориентированного графа D через L(П) сумму длин дуг, входящих в путь П. (Каждая дуга считается столько раз, сколько она входит в путь П).

Величина L называется Длиной пути.

Если выбрать веса равными 1, то придем к ненагруженному графу.

Путь в нагруженном ориентированном графе из вершины V в вершину W, где V¹W, называется Минимальным, если он имеет наименьшую длину.

Аналогично определяется Минимальный путь в нагруженном графе.

Введем матрицу длин дуг C(D)=[Cij] порядка N, причем

Свойства Минимальных путей в нагруженном ориентированном графе

1) Если для » дуги , то » минимальный путь (маршрут) является простой цепью;

2) если минимальный путь (маршрут) то для » I,J : путь (маршрут) тоже является минимальным;

3) если − минимальный путь (маршрут) среди путей (маршрутов) из V в W, содержащих не более K+1 дуг (ребер), то − минимальный путь (маршрут) из V в U среди путей (маршрутов), содержащих не более K дуг (ребер).

Источник

Построение собственного графа при анализе таблиц

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Учебный центр “Центриум”

по теме: «Построение собственного графа при анализе таблиц»

по дисциплине Информатика

Матвеев Дмитрий Николаевич,

преподаватель информационных дисциплин

ЭТАПЫ УЧЕБНОГО ЗАНЯТИЯ

Что такое нагруженный граф?

На прошлых занятиях мы познакомились с тем, что же такое граф, узнали, какой граф называется ориентированным и порешали задачи на уже готовом графе. Сегодня же мы познакомимся с новым типом графов, а именно с нагруженным графом.

Нагруженный граф – это такой граф, у которого каждому ребру сопоставлено определенное число.

Чаще всего, в задачах ОГЭ и ЕГЭ это число обозначает расстояние от одной вершины до другой, или время, за которое можно пройти от одной вершины до другой.

Пример нагруженного графа:

Кратчайшее расстояние (время) от стартового до конечного пункта?

В задачах мы постоянно будем сталкиваться с вопросом определения кратчайшего расстояния от одного пункта до другого. Давайте разберемся, что же это значит.

Кратчайшим называется минимальное из множества всех возможных расстояние (время), за которое можно добраться от одного пункта до другого.

Единственная проблема заключается в том, что на практике нам редко будет дан уже готовый нагруженный граф. Чаще всего нам будет необходимо его построить с помощью данных, указанных в таблице.

Рассмотрим конкретный пример:

Между населенными пунктами А, Б, В, Г, Е, Ж, З построены дороги, протяженность которых указана в таблице (Если числа в ячейке нет, это значит, что прямая дорога между этими населенными пунктами отсутствует). Передвигаться можно только по построенным дорогам. Определите длину кратчайшего расстояния между пунктами А и З.

Давайте сначала разберёмся как читать эту таблицу. На самом деле она симметрична относительно линии из крестиков (это отражает то, что длина из условного пункта А в условный пункт Б равна длине из пункта Б в пункт А, и что граф не является ориентированным, т.е. двигаться можно в обе стороны). А дальше читаем по строчкам. Берем строчку А и видим, что числа стоят на пересечении со столбцами Б (28), В (20) и Г (28). Это значит то, что из А ведут дороги в Б, В, Г и им соответствует данные длины, и так далее.

Дальше строим граф.

При построении графа нужно учесть некоторые вещи:

Рёбра графа не должны пересекаться ни в коем случае! (Они могут пересекаться, но вы запутаетесь при решении гарантированно)

Точки, в которые приходит больше всего дорог, должны стоять примерно в центре графа (это скорее рекомендация)

Попробуем построить граф по этой таблице и получаем такую картину:

Дальше просто анализируем наш граф и избавляемся от дорог, которые заведомо нам не выгодны, т.е. слишком длинные. В конечном итоге мы должны зачеркнуть практически все дороги, чтобы у нас остался один единственный верный путь.

Тут мы можем избавиться от дороги АБ (можно пройти АВБ), от дорог ВБ и БЕ (можно пройти ВЕ), от дороги ВЖ (можно пройти ВЕЖ). И у нас остается два пути, через верх и через низ.

Подсчитываем оба варианта и видим, что через верх длина будет 42, а через низ 43. Делаем вывод, что через верх идти выгодней

Значит ответ на эту задачу: 42.

Найти кратчайшее расстояние от пункта А до пункта З.

Получаем следующий граф:

Преобразовываем этот граф, убирая все лишние дороги:

Ответ на эту задачу: 19

Практическая работа №3

Тема: Построение собственного графа при анализе таблиц

Цель работы: Отработка полученных на уроке навыков

Найдите кратчайшее расстояние от пункта А до пункта Ж

Найдите кратчайшее расстояние от пункта А до пункта К

Найдите кратчайшее расстояние от пункта А до пункта Н

Найдите кратчайшее расстояние от пункта А до пункта К

Найдите кратчайшее расстояние от пункта А до пункта М

Самостоятельная работа №3

Тема: Построение собственного графа при анализе таблиц

Цель работы: Оценивание приобретенных на уроке навыков

Найдите кратчайшее расстояние от пункта А до пункта F

Найдите кратчайшее расстояние от пункта А до пункта М

Найдите кратчайшее расстояние от пункта A до пункта L

Найдите кратчайшее расстояние от пункта А до пункта К

Найдите кратчайшее расстояние от пункта А до пункта Н

Источник

Нагруженные графы. Расстояния в нагруженном графе

Дата добавления: 2015-07-23 ; просмотров: 1934 ; Нарушение авторских прав

Таким образом, в нагруженном графе (нагруженном орграфе) каждому ребру (дуге) x 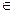X поставлено в соответствие некоторое действительное число l(x).

Значение l(x) называется длинойребра (дуги) x или весом ребра (дуги) x.

Информацию о длинах дуг (ребер) нагруженного орграфа (графа) можно представить в виде матрицы длин дуг (ребер).

Определение: Матрицей длин дуг (ребер)орграфа Д (графа G) называется квадратная матрица порядка n С= [с_ij], у которой каждый элемент с_ij определяется следующим образом:

Определение: Пусть дан нагруженный граф G = (V, X) (орграф Д = (V, X)).

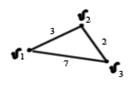
Рассмотрим некоторый маршрут (путь) из вершины v_i в вершину v_j. Обозначим его П, а сумму длин входящих в него ребер (дуг) обозначим l(П).

l(П) называется длиной маршрута (пути) П в нагруженном графе (орграфе) или весом маршрута (пути).

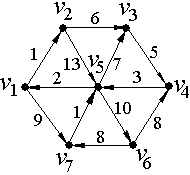
Пример: Пусть П – маршрут из v₁ в v₃.

Определение: Расстоянием в нагруженном графе (орграфе) (или взвешенным расстоянием) между вершинами v_i и v_j называется длина минимального маршрута (пути) из v_i в v_j.

Матрица взвешенных расстояний, взвешенные эксцентриситеты вершин, диаметр, радиус, центр нагруженного графа определяются аналогично определению данных понятий для ненагруженного графа.

Не нашли то, что искали? Google вам в помощь!

Источник

1.6. Матрицы достижимости и связности

S ( G)=sign[ E+ A+ A 2 + A 3 +… A n-1 ] ( E— единичная матрица порядка n ).

1.7. Расстояния в графе

Расстояние в графе удовлетворяют аксиомам метрики

2) (в неориентированном графе)

3)

4) в связном неориентированном графе.

Пусть связный граф (или псевдограф).

Радиусом графа G называется величина

1.8. Образ и прообраз вершины и множества вершин

1.9. Нагруженные графы

Цифра над дугой (см. рис. 5)− вес дуги (цена дуги).

Обозначения: для любого пути П нагруженного ориентированного графа D через l (П) сумму длин дуг, входящих в путь П. (Каждая дуга считается столько раз, сколько она входит в путь П).

Величина l называется длиной пути.

Если выбрать веса равными 1, то придем к ненагруженному графу.

Аналогично определяется минимальный путь в нагруженном графе.

Свойства минимальных путей в нагруженном ориентированном графе

1.10. Деревья и циклы

Граф G называется деревом если он является связным и не имеет циклов.

Следующие утверждения эквивалентны:

1) Граф G есть дерево.

2) Граф G является связным и число его ребер ровно на 1 меньше числа вершин.

3) » две различные вершины графа G можно соединить единственной (и при этом простой) цепью.

4) Граф G не содержит циклов, но, добавляя к нему любое новое ребро, получаем ровно один и притом простой цикл

Утверждение 4. Если у дерева G имеется, по крайней мере, 1 ребро, то у него найдется висячая вершина.

Остовным деревом связного графа G называется любой его подграф, содержащий все вершины графа G и являющийся деревом.

Пусть G – связный граф. Тогда остовное дерево графа G должно содержать n ( G )-1 ребер. Значит, для получения остовного дерева из графа G нужно удалить ребер.

Источник