Что такое наибольший делитель
Как находить наибольший общий делитель (НОД) двух чисел
Одной из задач, вызывающих проблему у современных школьников, привыкших к месту и не к месту использовать калькуляторы, встроенные в гаджеты, является нахождение наибольшего общего делителя (НОД) двух и более чисел.
Невозможно решить никакую математическую задачу, если неизвестно, о чём собственно спрашивают. Для этого нужно знать, что означает то или иное выражение, используемое в математике.
Общие понятия и определения
Необходимо знать:
В математике приняты следующие записи:
Различные способы найти НОД
Проще всего ответить на вопрос как найти НОД в том случае, когда меньшее число является делителем большего. Оно и будет в подобном случае наибольшим общим делителем.
Например, НОД (15;45) = 15, НОД (48;24) = 24.
Но такие случаи в математике являются весьма редкими, поэтому для того, чтобы находить НОД используются более сложные приёмы, хотя проверять этот вариант перед началом работы все же весьма рекомендуется.
Способ разложения на простые сомножители
Если необходимо найти НОД двух или более различных чисел, достаточно разложить каждое из них на простые сомножители, а затем произвести процесс умножения тех из них, которые имеются в каждом из чисел.
Пример 1
Рассмотрим, как находить НОД 36 и 90:
НОД (36;90) = 1*2*3*3 = 18.
Теперь посмотрим как находить то же самое в случае трёх чисел, возьмём для примера 54; 162; 42.
Как разложить 36 мы уже знаем, разберёмся с остальными:
Таким образом, НОД (36;162;42) = 1*2*3 = 6.
Следует заметить, что единицу в разложении писать совершенно необязательно.
Рассмотрим способ, как просто раскладывать на простые множители, для этого слева запишем необходимую нам цифру, а справа станем писать простые делители.
Разделять колонки можно, как знаком деления, так и простой вертикальной чертой.
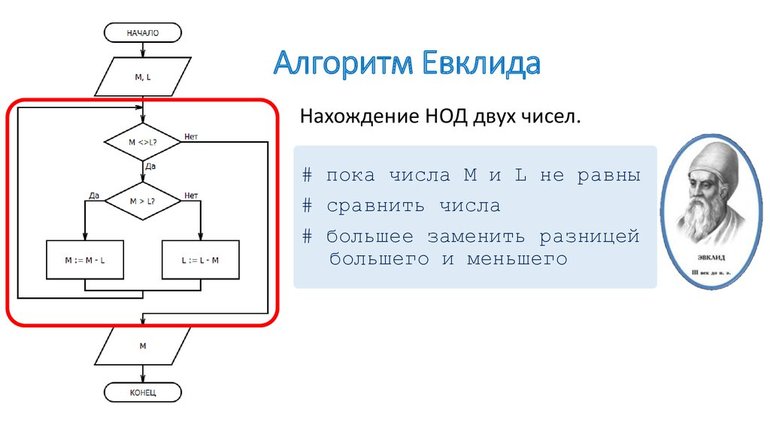
Евклидов способ
Этот вариант известен человечеству ещё со времён древнегреческой цивилизации, он во многом проще, и приписывается великому математику Евклиду, хотя весьма похожие алгоритмы применялись и ранее. Этот способ заключается в использовании следующего алгоритма, мы делим большее число с остатком на меньшее. Затем наш делитель делим на остаток и продолжаем так действовать по кругу пока не произойдёт деление нацело. Последнее значение и окажется искомым наибольшим общим делителем.
Приведём пример использования данного алгоритма:
попробуем выяснить какой НОД у 816 и 252:
Итак, по завершении нашего процесса мы получили НОД (816;252) = 12.
Действия при необходимости определения НОД если задано более двух значений
Мы уже разобрались, что делать в случае, когда имеется два различных числа, теперь научимся действовать, если их имеется 3 и более.
При всей кажущейся сложности, данная задача проблем у нас уже не вызовет. Сейчас мы выбираем два любые числа и определяем искомое для них значение. Следующим шагом отыскиваем НОД у полученного результата и третьего из заданных значений. Затем снова действуем по уже известному нам принципу для четвёртого пятого и так далее.
Заключение
Итак, при кажущейся большой сложности поставленной перед нами изначально задачи, на самом деле все просто, главное уметь выполнять безошибочно процесс делений и придерживаться любого из двух описанных выше алгоритмов.
Видео
С помощью видео вы сможете узнать, как найти наибольший общий делитель.
Наибольший общий делитель
Если натуральное число делится только на 1 и на само себя, то оно называется простым.
Любое натуральное число всегда делится на 1 и на само себя.
Число 2 — наименьшее простое число. Это единственное чётное простое число, остальные простые числа — нечётные.
Но многие натуральные числа делятся нацело ещё и на другие натуральные числа.
Числа, на которые число делится нацело (для 12 это 1, 2, 3, 4, 6 и 12 ) называются делителями числа.
Делитель натурального числа a — это такое натуральное число, которое делит данное число « a » без остатка.
Натуральное число, которое имеет более двух делителей называется составным.
Общий делитель двух данных чисел « a » и « b » — это число, на которое делятся без остатка оба данных числа « a » и « b ».
Наибольший общий делитель (НОД) двух данных чисел « a » и « b » — это наибольшее число, на которое оба числа « a » и « b » делятся без остатка.
Кратко наибольший общий делитель чисел « a » и « b » записывают так:
Делители чисел в записи решения обозначают большой буквой «Д».
Как найти наибольший общий делитель
Чтобы найти НОД двух или более натуральных чисел нужно:
Вычисления удобно записывать с помощью вертикальной черты. Слева от черты сначала записываем делимое, справа — делитель. Далее в левом столбце записываем значения частных.
Ответ: НОД (28; 64) = 4
Оформить нахождение НОД можно двумя способами: в столбик (как делали выше) или «в строчку».
Первый способ записи НОД

Второй способ записи НОД
На нашем информационном сайте вы также можете с помощью программы помощника найти наибольший общий делитель онлайн, чтобы проверить свои вычисления.
Понятие НОД
Определение, что такое НОД в математике, звучит следующим образом: наибольший делитель, общий для чисел a и b, есть такое наибольшее число, на которое описанные значения смогут разделиться без остатка.
Для наилучшего понимания того, как найти НОД двух чисел, вместо указанных переменных достаточно подставлять простые числа, например, 12 и 9. То есть самым наименьшим делимым числом для 12 и 9 является то, которое позволяет найти решение без остатка.
Задача по нахождению НОД может решаться тремя способами. Каждый из них применяется в зависимости от того, насколько быстро требуется найти необходимый показатель:
Лучше всего рассматривать применение указанных методов через определенный класс задач, которые помогают при дальнейшем изучении теорем, касающихся дробей. Формулы для указанной темы очень доступны для понимания ученикам и учителям.
Метод разложения
Суть второй методики заключается в разложении на простые множители и перемножении общих из них. В качестве примера можно рассмотреть представление НОД для показателей 18 и 24:
Способ является достаточно простым. Однако из-за некоторого объема операций можно оказаться в сложной ситуации с поиском общих делителей, поэтому следует рассмотреть еще один способ.
Вычеркивание показателей
Для третьей методики характерно вычеркивание из разложения тех показателей, которые не проходят во второе число. Есть такие виды НОД, которые могут сильно отличаться, но все равно позволяют найти нужный показатель. Например, нужно найти наибольший делитель для значений 28 и 16:
Аналогично можно отыскать для других значений, например, 100 и 40. После разложения из первого перечеркивается лишняя пятерка. Перемножение дает 20, который после поверки оказывается наибольшим делителем.
Несколько значений
Несмотря на кажущуюся сложность, доказать, что возможно найти НОД для нескольких чисел без помощи онлайн-калькуляторов, вполне реально. Значения, подлежащие поиску, необходимо разложить на множители. После чего ищется произведение общих простейших множителей.
Есть такие числа как 18, 24 и 36. Разложение 18 дает такие коэффициенты как 1, 2, 3, 6, 9 и 18. Затем 24 и 36 необходимо править по аналогичному методу. Если составить таблицу, то можно найти следующие общие показатели в виде 2 и 3. Они считаются общими для всех трех чисел.
Перемножив между собой, получается делимое число 6. Оно также подходит под разложение 18, 24 и 36, а также считается наибольшим общим делителем для всех трех параметров. Аналогичный принцип срабатывает и для четырех и более чисел, когда потребуется найти делитель на любом уровне сложности вплоть до максимального.
Наименьшее общее кратное
Помимо НОД, существует еще и наименьшее общее кратное, или НОК. Если сказать по-другому, то таковым свойством можно считать число, которое без остатка будет разделяться на число a и число b.
Как и для НОД, поиск НОК может осуществляться тремя похожими с предшествующими способами. Каждым из них можно воспользоваться в зависимости от ситуации и удобства решения задания:
На последнем методе стоит остановиться несколько подробнее. Он является не только сравнительно менее громоздким, но и обладает определенным преимуществом в виде уже найденного НОД и более простого алгоритма решения.
Совмещение делителей
Такая методика характерна для тех примеров, в которых требуется единовременное нахождение НОД и НОК двух чисел. Например, необходимо отыскать для чисел 24 и 12 НОК и НОК. Действовать нужно в следующем порядке:
Сходный механизм действует и при поиске НОК и НОД исходя из другой пары чисел. В каждом примере необходимо сначала отыскать наибольший делитель, перемножить два числа и получить наименьшее кратное.
Что касается решения с помощью интернет-ресурсов, то на сегодняшний день имеется много онлайн-калькуляторов и программ, которые дают возможность сравнительно быстро найти НОД и НОК и подсказать грамотные пути решения.
Нахождение наибольшего делителя и НОК является не только распространенной, но и сравнительно трудной задачей для учеников средней школы. Ведь если не рассмотреть подробно такую тему, то дальнейшее изучение дробей, которые включают в себя числитель и знаменатель, окажется практически невозможным.
Важно грамотно использовать ресурсы на специальных математических сайтах, где могут подробно и понятно объяснить разложение дробей и нахождение общих делителей. Бояться ошибиться в такой теме не стоит, поскольку при правильном подходе она пройдет достаточно быстро, а вычисление различных по уровню сложности примеров не составит особых сложностей.
Нахождение наибольшего общего делителя
В данной статье мы рассмотрим определение наибольшего общего делителя, научимся его находить для двух или нескольких чисел, а также разберем практические примеры для закрепления изложенного материала.
Определение наибольшего общего делителя
Если у числа больше двух делителей, его называют составным.
В отличие от кратных, количество делителей числа ограничено.
Общий делитель двух натуральных чисел – это такое число, на которое оба этих числа делятся без остатка.
Наибольший общий делитель двух натуральных чисел – наибольшее число из общих делителей данных чисел. Обозначается как НОД.
Например, НОД (12, 24) – это наибольший общий делитель чисел 12 и 24.
Нахождение НОД
Чтобы найти наибольший общий делитель, можно применить один из способов ниже.
Для двух (или небольших) чисел
Пример
Найдем наибольший делитель чисел 18 и 30.
Таким образом, НОД (18, 30) = 6.
Для нескольких (или больших) чисел
Этот метод обычно применяется, если приходится иметь дело с большим числами, или нужно найти НОД для нескольких чисел.
Пример
Найдем НОД (16, 24, 40).
Решение
Разложим эти числа на простые множители.
Для всех трех чисел одинаковыми являются три множителя – это три двойки.
Следовательно, НОД (16, 24, 40) = 2 ⋅ 2 ⋅ 2 = 8.
Вычисление НОД — ошибка, которой не замечают
Что такое НОД, все знают еще со школы. Для тех, кто подзабыл, напомню: НОД — наибольший общий делитель, делящий два целых числа без остатка. Например, НОД чисел 100 и 45 равен 5, а НОД чисел 17 и 7 равен 1. Существует несколько различных алгоритмов поиска этого числа. Однако, несмотря на то, что это достаточно простые алгоритмы, часто совершают одну маленькую, но очень существенную ошибку.
Алгоритмы вычисления НОД
Естественно, чаще всего пишут первый вариант — он легко запоминается, быстро пишется и достаточно быстро работает.
Претесты
Реализации корректно работают на таких тестах:
Естественно, они будут работать и на подобных тестах, где в качестве аргументов выступают целые неотрицательные числа. Но что, если…
Первые тесты с подвохом
… если заменить одно из чисел нулем? Например так:
Классический алгоритм Евклида (№3) уже попадает в бесконечный цикл.
Копаем глубже
Согласно определению, НОД может быть определен для любых двух целых чисел. Так почему бы не попробовать тесты, где одно из чисел — отрицательное:
Все становится еще интереснее. Первые две реализации выдают в качестве ответа -5. Третий алгоритм снова попадает в бесконечный цикл. Вместе с ним в бесконечном цикле оказывается пятый алгоритм. Четвертый падает по StackOverFlow — скорее всего тоже попадает в бесконечный цикл.
Но ведь ответ -5 — неправильный. По определению НОД — наибольший общий делитель. А таковым является число 5. Ведь и первое, и второе число делятся без остатка на 5. Значит и первые две реализации не дают верный ответ.
Почему решения №№3-5 попадают в бесконечный цикл?
Алгоритм Евклида попадает в цикл из-за бесконечного увеличения аргументов, если один из них отрицательный. Действительно, если посмотреть на эти строки, то можно заметить, что при отрицательном a (или b) операция вычитания заменяется сложением.
Аналогичное происходит в четвертом и пятом алгоритме:
В ситуации, когда a или b равны 0, то происходит бесконечное вычитание нуля, которое никаким образом не меняет значения аргументов.
Так что же не так?
Все эти алгоритмы корректны для входных данных, когда оба числа a и b — целые неотрицательные числа. Но вспомним еще раз — НОД существует для любых двух целых чисел.
Что же делать?
В качестве аргументов в функцию можно передавать абсолютное значение чисел, тогда ответ будет корректен:
Второй способ решения задачи — возвращать абсолютное значение ответа:
Второй вариант гораздо предпочтительнее: будет производиться меньше лишних вычислений, чем в первом варианте.
Итоги
Мы рассмотрели пять различных вариантов вычисления наибольшего общего делителя. Для каждого из них мы указали входные данные, на которых ответ существует, но решение «падает», а также способ решения проблемы.
Такие небольшие ошибки чаще всего допускаются по причине того, что не замечают «скользкие» места решения какой-то задачи. Часть из них отлавливается в процессе тестирования, а часть остается незамеченной.
В ситуации с вычислением НОД почти все реализации приведены с ошибкой. В Сети я нашел лишь парочку корректно работающих решений, остальные идентичны тем, что приведены в начале поста.