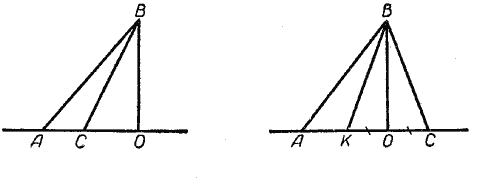Что такое наклонная и проекция наклонной
Геометрия. 10 класс
Конспект урока
Геометрия, 10 класс
Урок №10. Перпендикуляр и наклонные
Перечень вопросов, рассматриваемых в теме.
Теорема о трех перпендикулярах: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.
Обратная теорема: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции.
Определение: углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и ее проекцией на плоскость.
Атанасян Л. С., Бутузов В. Ф. Кадомцев С. Б. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы: учеб. для общеобразоват. организаций: базовый и углубл. уровни. – 4-е изд. – М.: Просвещение, 2017. – 255 с.
Глазков Ю. А., Юдина И. И., Бутузов В. Ф. Рабочая тетрадь по геометрии для 10 класса. Базовый и профильный уровень. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения
Рассмотрим плоскость α и точку А, не лежащую в этой плоскости (рис. 1). Проведем через точку А прямую, перпендикулярную к плоскости α, и обозначим буквой Н точку пересечения этой прямой с плоскостью α. Отрезок АН называется перпендикуляром, проведенным из точки А к плоскости α, а точка Н — основанием перпендикуляра. Отметим в плоскости α какую-нибудь точку М, отличную от Н, и проведем отрезок AM. Он называется наклонной, проведенной из точки А к плоскости α, а точка М – основанием наклонной. Отрезок НМ называется проекцией наклонной на плоскость α.
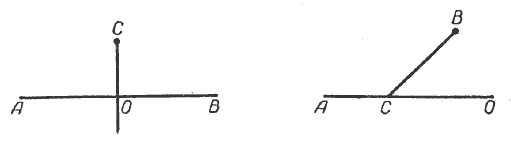
Наклонная к прямой
Что такое наклонная к прямой? Сколько наклонных можно провести из одной точки к данной прямой? Как найти расстояние между основаниями наклонных?
Наклонной, проведенной из точки A к прямой a, называется отличный от перпендикуляра отрезок, соединяющий точку A с некоторой точкой на прямой a.
Рисунок наклонной, проведенной из данной точки к данной прямой, начинают с изображения перпендикуляра (даже если в условии задачи о перпендикуляре не упоминается).
Чтобы нарисовать наклонную, нужно соединить точку, из которой проводится наклонная, с любой точкой на данной прямой.
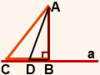
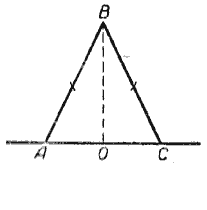
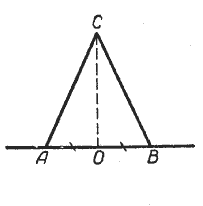
На рисунке 1 AB — перпендикуляр, проведенный из точки A к прямой a, AC — наклонная.
Точка B — основание перпендикуляра, точка C — основание наклонной AC.
Отрезок BC, соединяющий основание перпендикуляра с основанием наклонной, — проекция наклонной AC на прямую a.
Из точки к прямой можно провести бесконечно много наклонных.
Две наклонные проведенные из данной точки к данной прямой, могут быть расположены как по одну сторону от перпендикуляра, так и по разные стороны от него.
На рисунке 2 наклонные AC и AD расположены по одну сторону от перпендикуляра AB.
BC — проекция наклонной AC на прямую a,
BD — проекция наклонной AD на прямую a.
CD — расстояние между основаниями наклонных
Если наклонные расположены по одну сторону от перпендикуляра, чтобы найти расстояние между основаниями наклонных, надо найти разность между длинами их проекций.
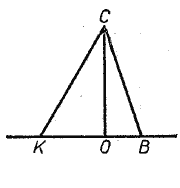
На рисунке 3 наклонные AC и AD расположены по разные стороны от перпендикуляра AB.
BC — проекция наклонной AC на прямую a,
BD — проекция наклонной AD на прямую a.
CD — расстояние между основаниями наклонных
Если наклонные расположены по разные стороны от перпендикуляра, расстояние между основаниями наклонных равно сумме длин проекций этих наклонных.
В следующий раз рассмотрим свойства наклонных.
2 Comments
Если наклонные расположены по разные стороны от перпендикуляра, расстояние между основаниями наклонных равно сумме длин проекций этих наклонных.
Перпендикуляр и наклонная к прямой
1. Проекция отрезка на прямую.
Если через какую-нибудь точку, взятую вне прямой, провести прямую, перпендикулярную к ней, то отрезок от данной точки до прямой для краткости называют одним словом перпендикуляр.
Если прямая, проведённая через данную точку, пересекает другую прямую, но не перпендикулярна к ней, то отрезок её от данной точки до точки пересечения с другой прямой называют наклонной к этой прямой.
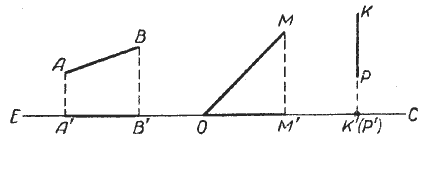
Если из концов какого-нибудь отрезка опустим перпендикуляры на произвольную прямую, то отрезок прямой, заключённый между основаниями перпендикуляров, называется проекцией отрезка на эту прямую.
Проекцией отрезка КР, перпендикулярного к ЕС, будет точка К’ (рис.).
2. Свойства перпендикуляра и наклонных.
Теорема 1. Перпендикуляр, проведённый из какой-нибудь точки к прямой, меньше всякой наклонной, проведённой из той же точки к этой прямой.
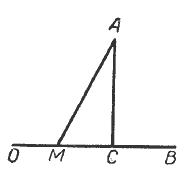
В ΔМАС отрезок АМ является гипотенузой, а гипотенуза больше каждого из катетов этого треугольника. Следовательно, АМ > АС. Так как наклонная АМ взята нами произвольно, то можно утверждать, что всякая наклонная к прямой больше перпендикуляра к этой прямой (а перпендикуляр короче всякой наклонной), если они проведены к ней из одной и той же точки.
Верно и обратное утверждение, а именно: если отрезок АС (рис.) меньше всякого другого отрезка, соединяющего точку АС любой точкой прямой ОВ, то он является перпендикуляром к ОВ. В самом деле, отрезок АС не может быть наклонной к ОВ, так как тогда он не был бы самым коротким из отрезков, соединяющих точку А с точками прямой ОВ. Значит, он может быть только перпендикуляром к ОВ.
Длина перпендикуляра, опущенного из данной точки на прямую, принимается за расстояние от данной точки до этой прямой.
Теорема 3 (обратная). Если две наклонные, проведённые к прямой из одной и той же точки, имеют равные проекции, то они равны между собой.
Требуется доказать, что АС = ВС.
Теорема 4. Если из одной и той же точки проведены к прямой две наклонные, то та из них больше, которая имеет большую проекцию на эту прямую.
1) Наклонные расположены по одну сторону перпендикуляра.
Угол АСЕ внешний по отношению к прямоугольному треугольнику СОВ (рис.), а поэтому ∠АСВ > ∠СОВ, т. е. он тупой. Отсюда следует, что АВ > СВ.
2) Наклонные расположены по обе стороны перпендикуляра. Для доказательства отложим на АО от точки О отрезок ОК = ОС и соединим точку К с точкой В (рис.). Тогда по теореме 3 имеем: ВК = ВС, но АВ > ВК, следовательно, АВ > ВС, т. е. теорема справедлива и в этом случае.
Теорема 5 (обратная). Если из одной и той же точки проведены к прямой две наклонные, то большая наклонная имеет и большую проекцию на эту прямую.
Между отрезками КО и ОВ может быть только одно из трёх соотношений:
КО не может быть меньше ОВ, так как тогда по теореме 4 наклонная КС была бы меньше наклонной ВС, а это противоречит условию теоремы.
Точно так же КО не может равняться ОВ, так как в этом случае по теореме 3 КС = ВС, что также противоречит условию теоремы.
Следовательно, остаётся верным только последнее соотношение, а именно, что КО > ОВ.
Определение перпендикуляра и наклонной
1) Определение перпендикуляра и наклонной.
Пусть дана плоскость и не лежащая на ней точка.
· Отрезок прямой, перпендикулярной плоскости, соединяющий данную точку с точкой на плоскости называется перпендикуляром из данной точки к данной плоскости.
· Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра.
· Любой отрезок, соединяющий данную точку с точкой на плоскости и не являющийся перпендикуляром к плоскости, называется наклонной.
· Конец отрезка, лежащий в плоскости, называется основанием наклонной.
2) Доказательство того, что перпендикуляр корочек наклонной
На рисунке 2 изображена плоскость α, перпендикуляр к ней AO, наклонная AB, а также показан отрезок BO, соединяющий основания наклонной и перпендикуляра. Отрезки AO, BO и AB образуют ΔAOB.
Рассмотрим ΔAOB, из определения перпендикуляра следует, что он прямоугольный. Перпендикуляр AO является катетом этого треугольника, а наклонная AB – его гипотенузой. Катет прямоугольного треугольника всегда меньше его гипотенузы (по теореме Пифагора), следовательно, перпендикуляр всегда короче наклонной.
3) Определение проекции
Отрезок, соединяющий основания перпендикуляра и наклонной, проведенных из одной и той же точки, называется проекцией наклонной.
Отрезок BO на рисунке 2 – является проекцией наклонной AB.
4) Теорема о сравнительной длине наклонных и их проекций
А) Любая наклонная больше своей проекции.
Вновь рассмотрим ΔAOB, изображенный на рис. 2, из определения перпендикуляра следует, что он прямоугольный. Проекция BO является катетом этого треугольника, а наклонная AB – его гипотенузой, т. к. катет прямоугольного треугольника всегда меньше его гипотенузы, следовательно, проекция наклонной на плоскость всегда короче самой наклонной.
Б) Равные наклонные имеют равные проекции
Доказательство: Рассмотрим треугольники AOB и AOD, они равны, т. к. равны их гипотенузы AB и AD, и углы AOB и AOD (они прямые), а сторона AO у них общая. Из равенства треугольников следует и равенство их сторон BO = OD, что и требовалось доказать.
В) Если проекции наклонных равны, то и наклонные равны. Доказывается аналогично утверждению Б.
Г) Большей наклонной соответствует большая проекция.
Рассмотрим прямоугольные треугольники AOB и AOD, AB > AD.


Но так как AB > AD => AB2 > AD2 => 

=> BO > DO. Что и требовалось доказать.
Д) Из двух наклонных больше та, у которой проекция больше. Доказывается аналогично Г.
Перпендикуляр и наклонная. Расстояние от прямой до плоскости
Перпендикуляром, опущенным из данной точки на данную плоскость, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости. Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра.
Расстоянием от точки до плоскости называется длина перпендикуляра, опущенного из этой точки на плоскость.
Наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости. Конец отрезка, лежащий в плоскости, называется основанием наклонной. Отрезок, соединяющий основания перпендикуляра наклонной, проведенных из одной и той же точки, называется проекцией наклонной.
Первый способ.
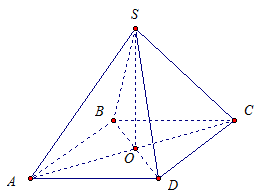
Имеем квадрат, центр квадрата точка – О, SО – перпендикуляр. Значит, для наклонной SC отрезок ОС есть проекция.
Прямая ВD перпендикулярна прямой ОС, которая является проекцией наклонной SC, значит, по теореме о трех перпендикулярах, прямая ВD перпендикулярна наклонной SC.
Второй способ.
Прямая SО перпендикулярна плоскости АВС, а значит – и прямой ВD, лежащей в ней.
Прямая ВD перпендикулярна SО и прямая ВD перпендикулярна прямой АС по свойству квадрата.
Получаем, что прямая ВD перпендикулярна двум пересекающимся прямым плоскости SОС, значит, она перпендикулярна ко всей плоскости SОС, а значит – и к прямой SC, лежащей в этой плоскости.
Расстояние от точки до плоскости есть перпендикуляр, опущенный на эту плоскость, то есть расстояние от точки А до плоскости a, есть длина перпендикуляра АВ.
В единичном тетраэдре DABC найдите расстояние от точки C до плоскости ADB.
Основанием прямого параллелепипеда служит параллелограмм с углом 120 \(^\circ\) и сторонами, равными 3 и 4. Меньшая диагональ параллелепипеда равна большей диагонали основания. Найдите объем параллелепипеда.
Расстояние от точки М до каждой из вершин правильного треугольника ABC равно 4 см. Найдите расстояние от точки М до плоскости ABC, если АВ = 6 см.
Через вершину А прямоугольника АВСD проведена прямая АК, перпендикулярная его плоскости. Расстояния от точки К до других вершин прямоугольника равны 12 м, 14 м, 18 м. Найдите отрезок АК.
Отрезок АD перпендикулярен к плоскости равнобедренного треугольника АВС.
АВ = АС = 10 см, ВС = 12 см, AD = 6 см.
Найдите расстояние от точки D до ВС.
Через вершину прямоугольника ABCD проведена прямая АК, перпендикулярная к плоскости прямоугольника.