Что такое наклонная в геометрии 7 класс
Наклонная к прямой
Что такое наклонная к прямой? Сколько наклонных можно провести из одной точки к данной прямой? Как найти расстояние между основаниями наклонных?
Наклонной, проведенной из точки A к прямой a, называется отличный от перпендикуляра отрезок, соединяющий точку A с некоторой точкой на прямой a.
Рисунок наклонной, проведенной из данной точки к данной прямой, начинают с изображения перпендикуляра (даже если в условии задачи о перпендикуляре не упоминается).
Чтобы нарисовать наклонную, нужно соединить точку, из которой проводится наклонная, с любой точкой на данной прямой.
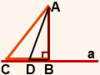
На рисунке 1 AB — перпендикуляр, проведенный из точки A к прямой a, AC — наклонная.
Точка B — основание перпендикуляра, точка C — основание наклонной AC.
Отрезок BC, соединяющий основание перпендикуляра с основанием наклонной, — проекция наклонной AC на прямую a.
Из точки к прямой можно провести бесконечно много наклонных.
Две наклонные проведенные из данной точки к данной прямой, могут быть расположены как по одну сторону от перпендикуляра, так и по разные стороны от него.
На рисунке 2 наклонные AC и AD расположены по одну сторону от перпендикуляра AB.
BC — проекция наклонной AC на прямую a,
BD — проекция наклонной AD на прямую a.
CD — расстояние между основаниями наклонных
Если наклонные расположены по одну сторону от перпендикуляра, чтобы найти расстояние между основаниями наклонных, надо найти разность между длинами их проекций.
На рисунке 3 наклонные AC и AD расположены по разные стороны от перпендикуляра AB.
BC — проекция наклонной AC на прямую a,
BD — проекция наклонной AD на прямую a.
CD — расстояние между основаниями наклонных
Если наклонные расположены по разные стороны от перпендикуляра, расстояние между основаниями наклонных равно сумме длин проекций этих наклонных.
В следующий раз рассмотрим свойства наклонных.
2 Comments
Если наклонные расположены по разные стороны от перпендикуляра, расстояние между основаниями наклонных равно сумме длин проекций этих наклонных.
Презентация: «Перпендикуляр, наклонная, ГМТ», 7 класс
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Перпендикуляр и наклонная Свойство биссектрисы угла Геометрическое место точек Задачи
Проекцией точки С на прямую АВ называется основание С0 перпендикуляра, опущенного из точки С на эту прямую. ССо┴ АВ Точка Со есть проекция точки С на прямую АВ Со = прАВС Свойство перпендикуляра и наклонных
Теоремы о перпендикуляре и наклонной т.2 Если проекции наклонных, проведенных из одной точки, равны, то равны и сами наклонные. Дано: СD и СF – наклонные CoD=прABСD CoF=прABСF CoD=СоF Док-ть: СD=CF Док-во: ΔDCCo=ΔFCCo по СУС DCo=FCo, по усл. Co=90o, по построению CD=CF, ч.т.д. CCo – общая
Теоремы о перпендикуляре и наклонной т.3 (обратная) Если наклонные, проведенные из одной точки, равны, то равны и их проекции. Дано: СD и СF – наклонные CoD=прABСD CoF=прABСF CD=СF Док-ть: СоD=CоF Док-во: ΔDCF – равнобедренный, т.к. CD=CF, по усл. CCо – высота, она же и медиана CоD=CоF, ч.т.д.
Теоремы о перпендикуляре и наклонной т. 4 Из 2-х наклонных, проведенных из одной точки, та больше, которая имеет большую проекцию. т. 5 (обратная) Из 2-х наклонных, проведенных из одной точки, большая наклонная имеет большую проекцию Дом. Задание: т. 4-5 доказать самостоятельно § 10 теоремы 1-4 оформить в тетрадь
Расстояние от точки до прямой есть длина перпендикуляра, опущенного из этой точки на данную прямую Свойство перпендикуляра, проведенного к отрезку прямой через его середину. т. Если прямая перпендикулярна к отрезку АВ и проходит через его середину, то любая точка этой прямой равноудалена от концов отрезка АВ. т. (обратная) Если точка Р равноудалена от концов отрезка АВ, то она лежит на перпендикуляре к нему в его середине.
Свойство биссектрисы угла т. 1 Если луч есть биссектриса угла, то любая точка его равноудалена от сторон этого угла. т. 2 (обратная) Если любая точка луча ОС равноудалена от сторон угла АОВ, то луч ОС – биссектриса этого угла. Доказательство – самостоятельно!
Геометрическое место точек – ГМТ есть совокупность (множество) всех точек, удовлетворяющих некоторому условию, общему для всех этих точек и только для них. Окружность есть ГМТ плоскости, находящихся на данном расстоянии от данной точки плоскости. О – центр окружности r – радиус окружности А, В, С – точки окружности
Биссектриса угла есть геометрическое место точек, каждая из которых равноудалена от сторон этого угла Перпендикуляр к отрезку, проведенный через его середину есть геометрическое место точек, каждая из которых равноудалена от концов этого отрезка Биссектриса
Задачи 1. На прямой АВ найти точку, равноудаленную от сторон угла COD 2. Найти точку О, равноудаленную от сторон ΔАВС 3. Найти точку О, равноудаленную от вершин ΔАВС 4. На прямой АВ найти точку О, равноудаленную от точек E и F
Решение задач 1. На прямой АВ найти точку М, равноудаленную от сторон угла COD Проверь свой чертеж!
2. Найти точку О, равноудаленную от сторон ΔАВС Решение задач Проверь свой чертеж!
3. Найти точку О, равноудаленную от вершин ΔАВС Решение задач Проверь свой чертеж!
4. На прямой АВ найти точку О, равноудаленную от точек E и F Решение задач Проверь свой чертеж!
Спасибо за внимание! Волошина Н.Н.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-494341
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Утверждены сроки заключительного этапа ВОШ
Время чтения: 1 минута
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
В Якутии проведут первую в РФ федеральную олимпиаду по родным языкам
Время чтения: 1 минута
До конца 2024 года в РФ построят около 1 300 школ
Время чтения: 1 минута
Госдума приняла закон об использовании онлайн-ресурсов в школах
Время чтения: 2 минуты
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
НАКЛОННАЯ
Смотреть что такое «НАКЛОННАЯ» в других словарях:
НАКЛОННАЯ — к прямой l прямая, пересекающая прямую l под углом, отличным от прямого. Наклонная к плоскости прямая, пересекающая эту плоскость под углом, отличным от прямого … Большой Энциклопедический словарь
наклонная — сущ., кол во синонимов: 1 • линия (182) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
наклонная — к прямой l, прямая, пересекающая прямую l под углом, отличным от прямого. Наклонная к плоскости прямая, пересекающая эту плоскость под углом, отличным от прямого. * * * НАКЛОННАЯ НАКЛОННАЯ к прямой l, прямая, пересекающая прямую l под углом,… … Энциклопедический словарь
Наклонная — ж. разг. Наклонная плоскость. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
Наклонная — к прямой l, прямая, пересекающая прямую l под углом, отличным от прямого. Н. к плоскости прямая, пересекающая эту плоскость под углом, отличным от прямого … Большая советская энциклопедия
НАКЛОННАЯ — к прямой I прямая, пересекающая прямую Iпод углом, отличным от прямого. Н. к плоскости прямая, пересекающая эту плоскость под углом, отличным от прямого. БСЭ 3 … Математическая энциклопедия
НАКЛОННАЯ — Характеристика линии или плоскости, которая, пересекав другую линию или плоскость под углом, отличным от угла в 90°. В графически представлениях факторного анализа две оси, представляющие коррелир щие факторы, являются наклонными … Толковый словарь по психологии
наклонная поверхность подошвы рельса — Ндп. наклонная грань подошвы рельса Поверхность, соединяющая шейку рельса с боковой гранью подошвы. Примечания 1. В рельсах типов Р75, Р65, Р50, Р38, Р33, Р24, Р18, P11, Р8 и Р5 наклонная поверхность подошвы выполнена в виде прямой линии под… … Справочник технического переводчика
наклонная орбита — Любая орбита спутника, кроме экваториальных и полярных. Наклонные орбиты бывают эллиптические и круговые, синхронные и несинхронные. Термин “наклонная орбита” применим и к геостационарным спутникам, орбита которых из за нестабильности … Справочник технического переводчика
НАКЛОННАЯ ПЛОСКОСТЬ — НАКЛОННАЯ ПЛОСКОСТЬ, простейшее устройство, представляющее собой плоскость, приподнятую с одного края. Проще толкать груз (массой ) вверх по наклонной плоскости (под углом к горизонтали), чем поднимать его вертикально это дает МЕХАНИЧЕСКИЙ… … Научно-технический энциклопедический словарь
Презентация «Перпендикуляр и наклонная» 7 класс
Код для использования на сайте:
Скопируйте этот код и вставьте себе на сайт
Для скачивания поделитесь материалом в соцсетях
После того как вы поделитесь материалом внизу появится ссылка для скачивания.
Подписи к слайдам:
Я МОГУ ОПРЕДЕЛИТЬ ПО ЧЕРТЕЖУ:
-Чем является точка В?
— Чем является отрезок АВ?
— Чем является точка С?
— Чем является отрезок ВС?
— Сколько перпендикуляров можно опустить из одной точки на прямую?
— Сравните наклонную и перпендикуляр по длине. Что из них можно считать наименьшим расстоянием?
Точка В – основание перпендикуляра
Определение АВ – перпендикуляр В – основание перпендикуляра
Наклонной, проведённой из данной точки к данной прямой,
называется отрезок, соединяющий эту точку с любой точкой данной прямой,
отличной от основания перпендикуляра,
опущенного из данной точки к данной прямой
С – основание наклонной
Определение АВ – перпендикуляр В – основание перпендикуляра
с основанием наклонной,
С – основание наклонной
ВС – проекция наклонной
Свойства наклонных перпендикуляр
1) Если из одной точки к прямой проведены наклонная и перпендикуляр, то наклонная всегда больше перпендикуляра.
Перпендикуляр – это расстояние от точки до прямой
Проверочная работа 1. Какой отрезок является перпендикуляром? 2. Какая точка является основанием перпендикуляра? 3. Какие отрезки являются наклонными? 4. Какие отрезки являются проекциями наклонных? 5. Какой отрезок является расстоянием от точки М до КТ?
Проверочная работа 1. Какой отрезок является перпендикуляром? (MF) 2. Какая точка является основанием перпендикуляра? (F) 3. Какие отрезки являются наклонными? (MK MT) 4. Какие отрезки являются проекциями наклонных? (KF TF) 5. Какой отрезок является расстоянием от точки М до КТ? (MF)
Урок геометрии в 7 классе «Перпендикулярные прямые. Перпендикуляр, наклонная и её проекция»
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Краткосрочный план по геометрии
Взаимное расположение прямых
Специализированная гимназия №8 с обучением на трех языках имени М.Х. Дулати
Ф.И.О. учителя: Павленко Е.В.
Перпендикулярные прямые. Перпендикуляр, наклонная и её проекция
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу)
знать понятия перпендикуляра, наклонной и проекции наклонной;
доказывать и применять теорему о единственности перпендикуляра к прямой;
Знают понятия перпендикуляра, наклонной, проекции наклонной, расстояния от точки до прямой;
знают свойства наклонных и их проекций;
знают связь между перпендикуляром, наклонной и проекцией наклонной,
применяют эти понятия в ходе решения задач;
Применяют свойства о единственности перпендикуляра к прямой к исследовательской работе
Знает определение перпендикулярных прямых;
Знает понятие перпендикуляра, наклонной, проекции наклонной;
Применяет перечисленные свойства при решении задач;
Умеет определять расстояние от точки до прямой
Применяет теорему о единственности перпендикуляра к прямой
— комментировать доказательство теорем и решения задач ;
— оперировать понятиями и терминами раздела;
— описывать данные чертежа.
Предметная лексика и терминология
— параллельные, пересекающиеся, перпендикулярные прямые;
— внутренние накрест лежащие углы, внутренние односторонние углы, соответственные углы;
-свойства прямоугольного треугольника;
— перпендикуляр, наклонная, проекция.
Серия полезных фраз для диалога/письма
— если внутренние накрест лежащие углы при… ;
— если сумма внутренних односторонних углов при… ;
-если соответственные углы при… ;
-сумма острых углов прямоугольного треугольника … ;
Обучение на протяжении всей жизни : формирование критического мышления, умение работать в парах, уважение к окружающим, постоянное развитие ума, отношений и характера, творчество и критичность. Развитие у обучающихся устной речи, памяти, воспитание грамотности устной и письменной речи; развитие умений и навыков, которые будут способствовать самостоятельному обучению учащихся.
Использование навыков при построении отрезков и чертежей на уроках черчения, применение понятий наклонная, перпендикуляр, проекция на уроках физики
Признаки равенства прямоугольных треугольников.
Свойства прямоугольного треугольника.
П араллельные прямые, их признаки и свойства
Запланированные этапы урока
Запланированная деятельность на уроке
1 .Организационный момент
Приветствие, создание коллаборативной среды, эмоциональный настрой
Учащиеся говорят пожелания соседу по парте
2. Активизация познавательной деятельности
Стратегия «Проверь себя»
Форма работы: индивидуальная работа
Задание: найти соответствие чертежа, обозначения и названия. Соединить стрелочками:
Выполняют и оценивание по дескриптору.
Определяет параллельные прямые
Определяет перпендикулярные прямые
Определяет пересекающиеся прямые
Определяет совпадающие прямые
Взаимомооценивание – прием «Звезда»
Оранжевая звезда – 1 ошибка
Красная звезда – 2 и более ошибки
3. Раскрытие новой темы
Задание. Устно. «Закончите фразу … »
Общие предложения ко всем учащимся
если внутренние накрест лежащие углы при… ;
если сумма внутренних односторонних углов при… ;
если соответственные углы при… ;
сумма острых углов прямоугольного треугольника …
Формативное оценивание. Устные комментарии учителя
Работа с учебником. Прием «Чтение с пометками»
Индивидульная работа. Задание.
Ознакомьтесь с новой темой в учебнике с.79-81.
Выделите новые понятия
Проверка изученного материала:
Прослушайте утверждение. Если оно верное хлопните в ладоши, если неверное-молчите.
Учитель читает утверждения. Если утверждение верное, учащиеся хлопают в ладоши, если нет – молчат.
1) Две пересекающиеся прямые называются перпендикулярными, если они образуют четыре прямых угла.
2) Через каждую точку прямой можно провести бесконечное множество прямых, перпендикулярных данной
3) Если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и второй
4) Т очка пересечения прямых называется основанием перпендикуляра.
Самооценивание: прием «Сигналы руки»
Большой палец вверх – все правильные и неправильные утверждения определены верно
Большой палец вбок – 1 ошибка
Большой палец вниз – более 1 ошибки
4. Первичное закрепление темы
Задание . Дать определение первым трём отрезкам и указать название точек В и С (с целью 7.3.2.8 знать понятия перпендикуляра, наклонной и проекции наклонной )
Задание выполняется устно, учащимися проговариваются определения перпендикуляра, наклонной и проекции наклонной. Делают соответствующие выводы.
Работа у доски и параллельно класс работает в тетрадях
— пр и меняет по н я т и е накл о н н ой и п е рпенди к у ля р а;
Формативное оценивание. Устные комментарии учителя
Решение задач на готовых чертежах. С обратной стороны листа задания ответы предыдущей парты
Пары проверяют друг друга по методу «Летучка»
— пр и меняет по н я т и е накл о н н ой и п е рпенди к у ля р а;
— сравнивает отрезки и находит длины неизвестных элементов;
— и споль з у е т с войства п р ям о у голь н ого т р е у г ол ьн и к а;
Формативное оценивание. Устные комментарии учителя
— и споль з у е т с войства п р ям о у голь н ого т р е у г ол ьн и к а;
— н а х о д ит ра сс тоя ни е от точки до п рям о й.
Формативное оценивание. Письменные рекомендации учителя в тетради
Исследовательская работа (уровень С)
Проводится приемом «Мозговой штурм».
Каждый учащийся выполняет самостоятельно. Учитель при необходимости оказывает индивидуальную помощь учащимся.
Докажите, что для произвольной прямой и точки, ей не принадлежащей, существует единственный перпендикуляр, опущенный из данной точки на данную прямую.
Пусть АВ – прямая, С – точка, ей не принадлежащая.
Выберем на прямой АВ какую-нибудь точку D. Если прямая СD перпендикулярна АВ, то отрезок СD – искомый перпендикуляр. В противном случае отлоим от луча DА в плоскость, не содержащую точку С, угол АDС’, равный углу АDС. Точку С’ выберем так, чтобы отрезки DС и DС’ были равны. Точку пересечения прямых АС и СС’ обозначим Н. Треугольники СDН и С’DН равны (СD=С’D, DН – общая сторона, СDН = С’DН). Значит, СНD=С’DН, и, следовательно СНD – прямой. Таким образом, СН – искомый перпендикуляр, опущенный из точки С на прямую АВ.
За лучшее доказательство класс оценивает «сигналы рукой».
По рисунку 1 определите отрезки;
По рисунку 2 свяжите эти отрезки с жизненной ситуацией
Подведение итогов: прием « Закончи фразу…»
Формативное оценивание: Устные комментарии учителя