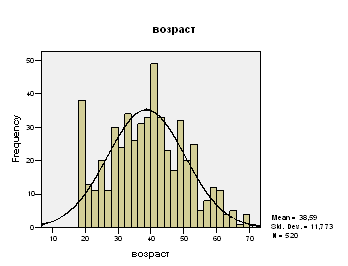
Что такое накопленный кумулятивный процент в таблице распределения частот

Кумулятивный частотный анализ выполняется, чтобы понять, насколько часто определенное явление (характеристика) оказывается ниже определенного значения. Это может помочь в описании или объяснении ситуации, в которой задействовано данное явление, или в планировании мероприятий, например, в защите от наводнений.

Этот статистический метод можно использовать для определения вероятности повторения такого события, как наводнение, в будущем, исходя из того, как часто оно происходило в прошлом. Его можно адаптировать к таким вещам, как изменение климата, вызывающее более влажную зиму и более сухое лето.

СОДЕРЖАНИЕ

Принципы

Определения

Кратко это выражение можно обозначить так:

В процентах уравнение гласит:

Оценка вероятности

От совокупной частоты

Существуют также другие предложения по знаменателю (см. Позиции построения ).

По методике ранжирования

Оценка вероятности упрощается за счет ранжирования данных.

Подгонка вероятностных распределений

Непрерывные распределения

Чтобы представить совокупное частотное распределение в виде непрерывного математического уравнения вместо дискретного набора данных, можно попытаться подогнать совокупное частотное распределение к известному совокупному распределению вероятностей.
В случае успеха известного уравнения будет достаточно, чтобы сообщить о частотном распределении, и таблица данных не потребуется. Кроме того, уравнение помогает интерполяции и экстраполяции. Однако следует проявлять осторожность при экстраполяции совокупного частотного распределения, поскольку это может быть источником ошибок. Одна из возможных ошибок состоит в том, что распределение частот больше не следует выбранному распределению вероятностей за пределами диапазона наблюдаемых данных.

Распределения вероятностей можно аппроксимировать несколькими способами, например:

Применение обоих типов методов с использованием, например,

часто показывает, что ряд распределений хорошо соответствует данным и не дает существенно различающихся результатов, в то время как различия между ними могут быть небольшими по сравнению с шириной доверительного интервала. Это показывает, что может быть трудно определить, какое распределение дает лучшие результаты. Например, приблизительно нормально распределенные наборы данных могут быть приспособлены к большому количеству различных распределений вероятностей. в то время как отрицательно искаженные распределения могут быть подогнаны под квадратные нормальные и зеркальные распределения Гамбеля.

Прерывистые распределения

Прогноз

Неопределенность

Доверительные интервалы

Теория вероятностей может помочь оценить диапазон, в котором может находиться случайная ошибка. В случае накопленной частоты есть только две возможности: превышено определенное опорное значение X или оно не превышено. Сумма частоты превышения и совокупной частоты составляет 1 или 100%. Следовательно, биномиальное распределение можно использовать для оценки диапазона случайной ошибки.

Согласно нормальной теории, биномиальное распределение можно аппроксимировать, а для больших N стандартное отклонение Sd можно рассчитать следующим образом:

Определение доверительного интервала от ПК позволяет использовать Т-критерий Стьюдента ( т ). Значение t зависит от количества данных и уровня достоверности оценки доверительного интервала. Затем нижний ( L ) и верхний ( U ) пределы достоверности Pc в симметричном распределении находятся по формуле:

где видно, что эти выражения для Pc = 0,5 совпадают с предыдущими.

Пример

N = 25, Pc = 0,8, Sd = 0,08, уровень достоверности 90%, t = 1,71, L = 0,58, U = 0,85 Таким образом, с достоверностью 90% установлено, что 0,58 0,85

Срок возврата

Период повторяемости T определяется как:

Потребность в поясах уверенности

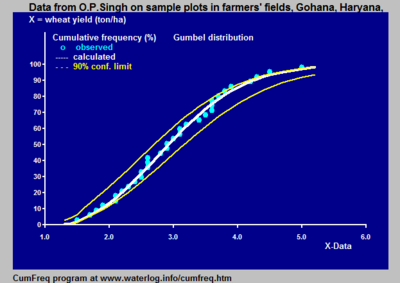
На рисунке показано изменение, которое может возникнуть при получении выборок переменной, соответствующей определенному распределению вероятностей. Данные были предоставлены Бенсоном.

Полоса уверенности вокруг экспериментальной кривой накопленной частоты или периода повторяемости дает представление о регионе, в котором может быть найдено истинное распределение.

Кроме того, он поясняет, что экспериментально найденное наиболее подходящее распределение вероятностей может отклоняться от истинного распределения.

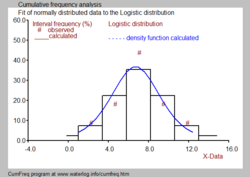
Гистограмма

Источник

Частоты

Команда Frequencies (Частоты) являются одной из самых простых и часто используемых команд SPSS. Действие команды сводится к подсчету количества объектов в каждой категории переменной. Эти и называется распределением частот по категориям переменной.

Для создания частотных распределений в меню Analyze (Анализ) нужно выбрать команду Descriptive Statistic (Описательные статистики), затем Frequencies (Частоты). Появится диалоговое окно.

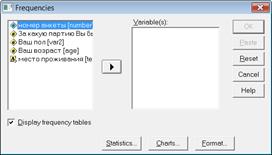
В левой части окна расположен список всех доступных переменных. В нем необходимо выбрать те переменные, для которых необходимо вычислить распределение частот. Для этого щелчком выделяется нужная переменная и с помощью кнопки с треугольником перемещается в целевой список Variable(s) (Переменные).

Если необходимо удалить переменную из целевого списка, достаточно выделить ее в нем, затем воспользоваться кнопкой с направленной влево стрелкой, переменная вновь переместиться в исходный список. Чтобы полностью очистить целевой список, можно щелкнуть на кнопке Reset (Сброс).

После создания целевого списка, для получения частотных распределений, нужно щелкнуть на кнопке ОК. Программа SPSS сформирует окно вывода с результатами выполнения команды.

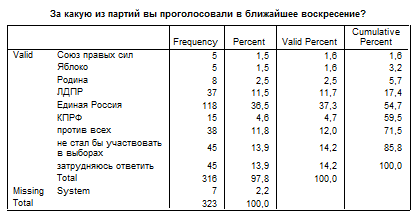
Пример частотного распределения вопроса: «За какую партию Вы голосовали бы в ближайшее воскресенье?» (опрос проводился в 2006 г.)

Ниже дана трактовка терминов, используемых программой в окне вывода данных.

§ Frequency (Частота) – число объектов, соответствующих каждой категории (градации) переменной (число респондентов, выбравших соответствующий вариант ответа)

§ Percent (Процент) – процент от общей численности (с учетом пропусков). Если в файле есть пропущенные значения, то их процент указан в предпоследней строке Missing System.

§ Valid percent (Валидный процент) – процент значений для каждой категории за вычетом пропущенных значений.

§ Cumulative percent (Кумулятивный процент) – накопленный процент величины Valid percent.

§ Valid (Валидные значения) – список градаций (значений) переменной.

§ Total (Итого) – итоговые значения.

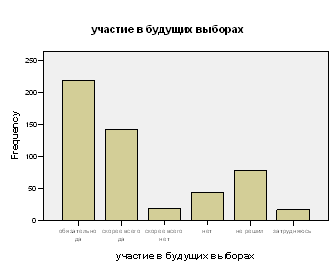
Столбиковые диаграммы. Для того, чтобы создать столбиковую диаграмму для дискретных данных (например, распределение респондентов по полу, предпочтений в выборе партий) необходимо в диалоговом окне Frequencies (Частоты) щелкнуть на кнопке Charts (Диаграммы) и выбрать тип диаграммы с помощью переключателей Bar charts (Столбиковая), Pie charts (Круговая), Histograms (Гистограмма). В зависимости от величины, которую нужно использовать для отображения частот, в группе Chart Values (Значения в диаграмме) устанавливается переключатель Frequencies (Частоты) Percentages (Проценты). Для закрытия диалогового окна нужно щелкнуть на кнопке Continue (Продолжить). Для завершения операции в диалоговом окне Frequencies щелкнуть на кнопке ОК. После этого программа сгенерирует диаграмму, соответствующую выбранной переменной. Созданные диаграммы можно просмотреть в окне вывода, просмотра данных.

Задание.1.По массиву данных opros.sav вычислить частотные (линейные) распределения вопросов: «Играет ли молодежь заметную роль в общественной жизни города?», «Как вы относитесь к политической деятельности?», «Удовлетворены ли вы уровнем своего образования?». Построить диаграммы. Проанализировать полученные данные.

2. Исходя из задач собственного исследования, создать линейные распределения для переменных анкеты. Построить диаграммы. Проанализировать полученные данные.

Источник

Кумулятивный частотный анализ

Кумулятивный частотный анализ выполняется, чтобы получить представление о том, как часто определенное явление (характеристика) оказывается ниже определенного значения. Это может помочь в описании или объяснении ситуации, в которой задействовано данное явление, или в планировании мероприятий, например, в защите от наводнений. [1]

Этот статистический метод можно использовать для определения вероятности повторения такого события, как наводнение, в будущем, исходя из того, как часто оно происходило в прошлом. Его можно адаптировать к таким вещам, как изменение климата, вызывающее более влажную зиму и более сухое лето.

СОДЕРЖАНИЕ

Принципы [ править ]

Определения [ править ]

Кратко это выражение можно обозначить так:

В процентах уравнение гласит:

Оценка вероятности [ править ]

От совокупной частоты [ править ]

Существуют также другие предложения по знаменателю (см. Позиции построения ).

По технике ранжирования [ править ]

Оценка вероятности упрощается за счет ранжирования данных.

Подбор вероятностных распределений [ править ]

Непрерывное распространение [ править ]

Чтобы представить совокупное частотное распределение в виде непрерывного математического уравнения вместо дискретного набора данных, можно попытаться подогнать совокупное частотное распределение к известному совокупному распределению вероятностей. [2] [3] В
случае успеха известного уравнения будет достаточно, чтобы сообщить о распределении частот, и таблица данных не потребуется. Кроме того, уравнение помогает интерполяции и экстраполяции. Однако следует проявлять осторожность при экстраполяции совокупного частотного распределения, поскольку это может быть источником ошибок. Одна из возможных ошибок состоит в том, что распределение частот больше не следует выбранному распределению вероятностей за пределами диапазона наблюдаемых данных.

Распределения вероятностей можно аппроксимировать несколькими способами, например [2] :

Применение обоих типов методов с использованием, например,

часто показывает, что ряд распределений хорошо соответствует данным и не дает существенно различающихся результатов, в то время как различия между ними могут быть небольшими по сравнению с шириной доверительного интервала. [2] Это показывает, что может быть трудно определить, какое распределение дает лучшие результаты. Например, приблизительно нормально распределенные наборы данных могут быть приспособлены к большому количеству различных распределений вероятностей. [4], в то время как отрицательно искаженные распределения могут быть подогнаны к квадратно-нормальным и зеркальным распределениям Гамбеля. [5]

Прерывистые распределения [ править ]

Прогноз [ править ]

Неопределенность [ править ]

Доверительные интервалы [ править ]

Теория вероятностей может помочь оценить диапазон, в котором может находиться случайная ошибка. В случае кумулятивной частоты есть только две возможности: определенное опорное значение Х превышается или не превышается. Сумма частоты превышения и совокупной частоты составляет 1 или 100%. Следовательно, биномиальное распределение можно использовать для оценки диапазона случайной ошибки.

Согласно нормальной теории, биномиальное распределение можно аппроксимировать, а для больших N стандартное отклонение Sd можно рассчитать следующим образом:

Определение доверительного интервала от ПК позволяет использовать Т-критерий Стьюдента ( т ). Значение t зависит от количества данных и уровня достоверности оценки доверительного интервала. Затем нижний ( L ) и верхний ( U ) пределы достоверности Pc в симметричном распределении находятся по формуле:

где видно, что эти выражения для Pc = 0,5 совпадают с предыдущими.

Пример

N = 25, Pc = 0,8, Sd = 0,08, уровень достоверности 90%, t = 1,71, L = 0,58, U = 0,85 Таким образом, с достоверностью 90% установлено, что 0,58 0,85

Период возврата [ править ]

Период повторяемости T определяется как:

Потребность в поясах уверенности [ править ]

На рисунке показано изменение, которое может возникнуть при получении выборок переменной, соответствующей определенному распределению вероятностей. Данные были предоставлены Бенсоном. [1]

Полоса уверенности вокруг экспериментальной кривой накопленной частоты или периода повторяемости дает представление о регионе, в котором может быть найдено истинное распределение.

Кроме того, он поясняет, что экспериментально найденное наиболее подходящее распределение вероятностей может отклоняться от истинного распределения.

Источник

Кумулятивная кривая распределения

График эмпирической функции распределения для непрерывного вариационного ряда называют кумулятивной кривой или просто кумулятой. Название происходит от английского слова accumulation – накопление.

При нахождении значений функции F_n(x) в числителе записывалась сумма некоторых частот. Эта сумма также имеет свое название – кумулятивная или накопленная частота соответствующего интервала. Дадим более точное определение.

Пусть дан вариационный интервальный ряд распределения частот.

Накопленной частотойn_i нак. i–го интервала называется сумма частоты данного интервала и частот всех предшествующих интервалов, т.е.

.

Нетрудно понять, что накопленная частота последнего интервала совпадает с объемом выборочной совокупности.

Аналогично, для каждого интервала можно определить накопленные частости.

Накопленной частостьюw_i нак. i–го интервала называется сумма частости данного интервала и частотей всех предшествующих интервалов, т.е.

.

Ясно, что накопленная частость последнего интервала равна 1.

Определив накопленные частости интервалов, можно иначе определить и кумуляту.

Пусть дан интервальный ряд распределения частостей

Кумулятой (кумулятивной кривой) интервального ряда распределения частостей называют графическое представление данного ряда в виде ломаной линии, вершины которой находятся в точках с координатами (a_i+1; w_i), i = 1, 2, …, m, при этом первая точка ломаной находится на оси абсцисс и имеет координаты (а₁; 0).

В качестве графического представления интервального ряда может быть рассмотрена ломаная с вершинами в точках (а₁; 0) и (a_i+1; n_i), i = 1, 2, …, m. В этом случае полученная кривая будет называться кумулятой распределения частот (а не частостей) интервального ряда.

Общий вид кумулят распределения частот и частостей будет один и тот же. Отличие состоит лишь в масштабе на оси ординат.

Пример 4.5. Для данного интервального ряда построить кумуляту распределения частот и кумуляту распределения частостей

Интервалы	1-3	3-5	5-7	7-9	9-11
Частоты интервалов

Решение. Объем статистической совокупности равен n = 20.

Дополним данный интервальный ряд тремя строками. В третьей строке запишем накопленные частоты интервалов, в четвертой – частости, в пятой – накопленные частости интервалов, получим

Интервалы	1-3	3-5	5-7	7-9	9-11
ni
ni нак
wi	0,15	0,3	0,35	0,15	0,05
wi нак	0,15	0,45	0,8	0,95

Кумулята распределения частот имеет вид:

Кумулята распределения частостей имеет вид:

По правилу, связанному с накопленными частотами и частостями, строят кумуляту и для дискретного вариационного ряда. Аналогично определяется накопленная частота и накопленная частость для варианта. Ломаная линия с вершинами в точках (x_i, n_i нак ), i = 1, 2, …, m будет определять кумуляту распределения частот дискретного ряда, а ломаная линия с вершинами в точках (x_i, w_i нак ), i = 1, 2, …, m – кумуляту распределения частостей дискретного ряда.

Пример 4.6. Построить кумуляту распределения частот и кумуляту распределения частостей для следующего дискретного ряда

Варианты хi

Частоты ni

Решение.Объем статистической совокупности равен n = 10. Дополним данный дискретный ряд тремя строками. В третьей строке запишем накопленные частоты вариантов, в четвертой – частости, в пятой – накопленные частости вариантов, получим

Варианты хi
Частоты ni
ni нак
wi	0,1	0,3	0,5	0,1
wi нак	0,1	0,4	0,9

Строим кумуляту распределения частот:

и кумуляту распределения частостей:

Для вариационных рядов существуют и другие графические представления.

Полигон распределения

Полигон распределения чаще всего используют для графического представления дискретных рядов.

Пусть дан дискретный ряд распределения частот (частостей).

Пример 4.7. Построить полигон распределения частот и полигон распределения частостей для следующего дискретного ряда:

Решение. Объем статистической совокупности равен 20. Дополним ряд одной строкой, где определим для каждого варианта частость, получим

Вариант
Частота
Частость	0,15	0,2	0,3	0,25	0,05	0,05

Полигон распределения частот имеет вид:

Полигон распределения частостей имеет вид:

Очевидно, что полигон распределения частостей дискретного ряда является статистическим (выборочным) аналогом многоугольника распределения дискретной случайной величины.

Для графического представления интервального ряда также может быть построен полигон. Однако вначале интервальный ряд преобразуют в дискретный, для чего каждый интервал заменяют на число, равное середине интервала и ставят в соответствие этому числу частоту (или частость) рассматриваемого интервала. Затем для полученного дискретного ряда строят полигон, который будет являться полигоном и для данного интервального ряда.

Пример 4.8. Построить полигон распределения частот для следующего интервального ряда:

Интервалы	2-5	5-8	8-11	11-14	14-17	17-20
Частоты

Решение.Объем статистической совокупности равен 16. Дополним таблицу одной строкой. В третьей строке запишем z_i – середины соответствующих интервалов, получим

Интервалы	2-5	5-8	8-11	11-14	14-17	17-20
Частоты
zi	3,5	6,5	9,5	12,5	15,5	18,5

Полигон распределения частот имеет вид:

Из теории вероятностей известно, что для непрерывной случайной величины имеется еще одна форма закона распределения – функция плотности распределения, график которой называется кривой распределения. Рассмотрим статистический аналог этого графика.

Источник