Что такое наложение отрезков

Сравнение отрезков

Одной из простейших геометрических фигур является отрезок. Для того чтобы сравнивать отрезки, можно использовать два способа:

Метод наложения:

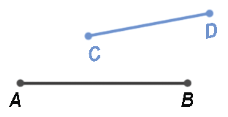
Пусть нам даны два отрезка AB и СD:

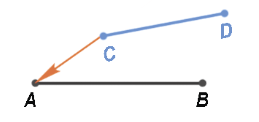
Совместим начало отрезка AB и СD (точки A и С).

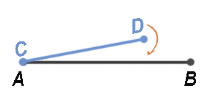
Затем повернем отрезок СD так, чтобы он совпал с отрезком AB.

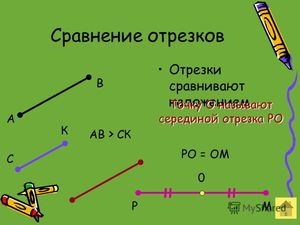
Мы видим, что отрезок СD составляет часть отрезка AB, следовательно, мы можем сделать вывод, что отрезок AB больше отрезка СD.

Если точка делит отрезок на равные отрезки, то эту точку называют серединой отрезка.

Рассмотрим еще одну пару отрезков HG и ST.

Совместим начало отрезка HG и ST.

Затем повернем отрезок ST так, чтобы он совпал с отрезком HG.

В данном случае мы видим, что совпали не только точки S и H (начала отрезков HG и ST), но и точки G и T (концы отрезков HG и ST), то есть отрезки совпадают, а нам известно, что две геометрические фигуры называются равными, если их можно совместить наложением.

Вывод:

Измерение длин:

Для измерения отрезков, необходимо наложить на него единичные отрезки, и длиннее будет считаться тот отрезок, которому соответствует большее число единичных отрезков.

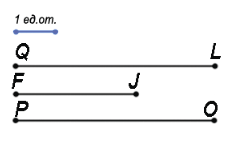
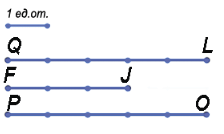
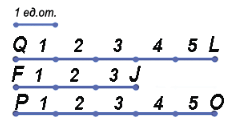
Пример: Пусть у нас есть единичный отрезок. Рассмотрим три отрезка QL, FJ и PO.

Наложим единичный отрезок на данные.

Посчитаем, какое количество единичных отрезков накладывается на каждый из отрезков, получаем: QL = 5 ед.от., FJ = 3 ед.от., PO = 5 ед. от.

Поделись с друзьями в социальных сетях:

Источник

Как сравнить два отрезка: способы и примеры

Отрезок — часть прямой, ограниченная двумя точками, кратчайшее расстояние между этими точками. Существует несколько способов сравнения геометрических фигур, выбор такого способа зачастую зависит не только от условия задачи, но и от возможностей. Как же сравнивать отрезки, расскажем в этой статье.

Способы сравнения двух отрезков

В геометрии две фигуры, имеющие одинаковый размер и форму, называются равными. Сравнение фигур дает возможность сказать, одинаковы ли они. Одним из способов является наложение. Если фигуры удается совместить наложением, они считаются равными.

Сравнить фигуры — значит, определить, которая из них длиннее или короче. Ответ должен быть определенным, нельзя сказать, что один отрезок длиннее или равен второму. В математике такой ответ неправилен, его можно приравнять к отсутствию ответа.

Записывают результат сравнения с помощью знаков больше, меньше и знака равенство (>; АБ.

Сравнивать фигуры можно разными способами, выбор которых зависит от возможностей или условий:

Лучше всего, если они различаются по длине визуально, и, просто посмотрев на них, вы можете сказать, который длиннее. Но так бывает не всегда.

Измерение длины

Самый простой способ — измерение. Для этого можно использовать линейку, просто измерив длину отрезка, мы поймем, который из них длиннее. Если нет линейки, но они начерчены на листе в клетку, для измерения их длин можно посчитать клетки. В одном сантиметре две клетки. Это метод сравнения измерением длин, но есть еще метод сравнения наложением.

Обратите внимание: что такое луч в геометрии.

Наложение друг на друга

Как происходит совмещение АБ и ВГ:

Сравнение в координатной сетке

Допустим, что у нас есть два отрезка, координаты которых мы знаем — а (Х1, Y1; Х2, Y2) и b (Х3, Y3; X4, Y4).

Первое, что нужно сделать — придать координатам числовые значения:

Da = √ ((-7 — 3) ² + (4 — (-4)) ²) = √ (-10 ² + 8 ²) = √ 100 + 64 = √ 164

Db = √ ((-3 — 0) ² + (-5 — (-3)) ²) = √ (-3 ² + (-8) ²) = √ (9+ 64) = √ 73

√ 164 > √ 73, значит, Da > Db.

Также можно сравнить отрезки, находящиеся в трехмерной системе координат, надо учитывать не две, а три координаты каждого из них.

Примеры

Рассмотрим сравнение методом наложения. У нас имеется два отрезка — АБ и ВГ.

Чтобы узнать, равны они или нет, просто приложим их друг к другу так, чтобы их «начала» были в одной точке, то есть совместим точки, А и В.

Если мы видим, что АБ получается частью ВГ, значит, он меньше, то есть АБ 2, значит, CD>AB, то есть отрезок CD длиннее AB.

Источник

Как сравнить два отрезка: способы и примеры

Отрезок — часть прямой, ограниченная двумя точками, кратчайшее расстояние между этими точками. Существует несколько способов сравнения геометрических фигур, выбор такого способа зачастую зависит не только от условия задачи, но и от возможностей. Как же сравнивать отрезки, расскажем в этой статье.

Способы сравнения двух отрезков

В геометрии две фигуры, имеющие одинаковый размер и форму, называются равными. Сравнение фигур дает возможность сказать, одинаковы ли они. Одним из способов является наложение. Если фигуры удается совместить наложением, они считаются равными.

Сравнить фигуры — значит, определить, которая из них длиннее или короче. Ответ должен быть определенным, нельзя сказать, что один отрезок длиннее или равен второму. В математике такой ответ неправилен, его можно приравнять к отсутствию ответа.

Записывают результат сравнения с помощью знаков больше, меньше и знака равенство (&gt,, &lt,, =). Например, длина отрезка АБ — 2 см, а ВГ — 8 см, записываем результат сравнения так: АБ &lt, ВГ или ВГ &gt, АБ.

Это интересно: как разложить на множители квадратный трехчлен?

Сравнивать фигуры можно разными способами, выбор которых зависит от возможностей или условий:

Лучше всего, если они различаются по длине визуально, и, просто посмотрев на них, вы можете сказать, который длиннее. Но так бывает не всегда.

Измерение длины

Самый простой способ — измерение. Для этого можно использовать линейку, просто измерив длину отрезка, мы поймем, который из них длиннее. Если нет линейки, но они начерчены на листе в клетку, для измерения их длин можно посчитать клетки. В одном сантиметре две клетки. Это метод сравнения измерением длин, но есть еще метод сравнения наложением.

Обратите внимание: что такое луч в геометрии.

Наложение друг на друга

Как происходит совмещение АБ и ВГ:

Бывает так, что при наложении одного отрезка на другой ровно половина одного из них будет совмещена с другим. Точку, которая делит его на две равные части, называют серединной точкой. И если у нас есть серединная точка В, то АВ=ВБ.

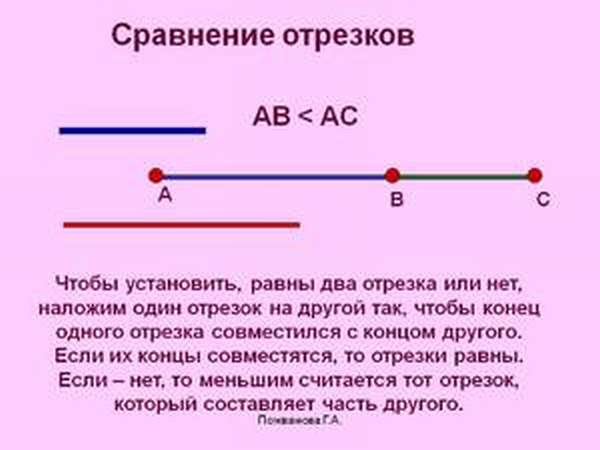
Примерно так же наложением сравнивают не только прямые, но и другие геометрические фигуры, а также углы.

Можно сделать «линейку» из полоски бумаги, при этом такую линейку не нужно линовать, достаточно отметить на ней начало и конец одного из отрезков. Затем вы прикладываете импровизированную линейку ко второму, совмещая его начало с первой отметкой и, сравниваете расположение второй отметки по отношению к его концу. Таким способом можно сравнивать и довольно большие фигуры, например, расстояние между столбиками забора, но использовать при этом лучше не бумажную полоску, а веревку.

Два отрезка называются равными, если их можно совместить методом наложения. Если есть возможность приложить их друг к другу, просто посмотрите, какой из них длиннее. Но так можно сделать не всегда.

Если под рукой имеется циркуль, поставьте одну ножку циркуля в начало, а другую в конец первого отрезка. Затем не сдвигая ножки циркуля, установите одну из них в начало второго и посмотрите, если вторая ножка циркуля в точке, обозначающей конец — они равны. Если вторая ножка на самой прямой — первый отрезок меньше, если за ним — первый больше.

Сравнение в координатной сетке

Допустим, что у нас есть два отрезка, координаты которых мы знаем — а (Х1, Y1, Х2, Y2) и b (Х3, Y3, X4, Y4).

Первое, что нужно сделать — придать координатам числовые значения:

Da = √ ((-7 — 3) ² + (4 — (-4)) ²) = √ (-10 ² + 8 ²) = √ 100 + 64 = √ 164

Db = √ ((-3 — 0) ² + (-5 — (-3)) ²) = √ (-3 ² + (-8) ²) = √ (9+ 64) = √ 73

√ 164 &gt, √ 73, значит, Da &gt, Db.

Также можно сравнить отрезки, находящиеся в трехмерной системе координат, надо учитывать не две, а три координаты каждого из них.

Примеры

Рассмотрим сравнение методом наложения. У нас имеется два отрезка — АБ и ВГ.

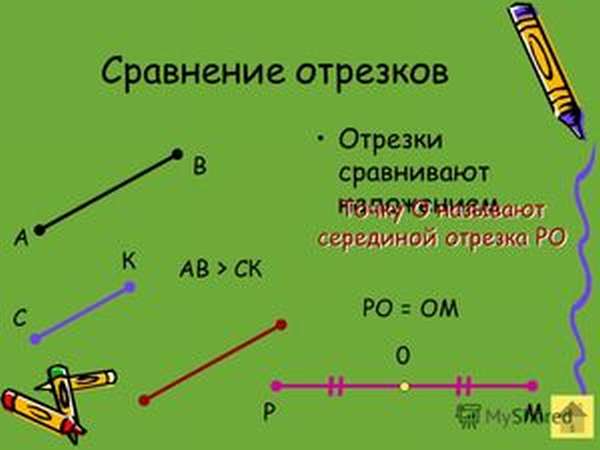
Чтобы узнать, равны они или нет, просто приложим их друг к другу так, чтобы их «начала» были в одной точке, то есть совместим точки, А и В.

Если мы видим, что АБ получается частью ВГ, значит, он меньше, то есть АБ&lt, ВГ, а если при наложении оба конца отрезков совмещаются — значит, они равны.

Теперь рассмотрим сравнение отрезков путем измерения. При помощи линейки вычисляем длину каждого отрезка. Например, длина AB = 2 см, а CD = 8 см. 8&gt,2, значит, CD&gt,AB, то есть отрезок CD длиннее AB.

Источник

Наложения и движения

При наложении различные точки отображаются в различные точки.

Доказательство:

Из этого утверждения мы можем сделать вывод, что при наложении отрезок отображается на равный ему отрезок. Пусть при наложении концы А и В отрезка АВ отображаются в точки А₁ и В₁. Тогда отрезок АВ отображается на отрезок А₁В₁ (т.к. согласно аксиоме, если при наложении совмещаются концы двух отрезков, то совмещаются и сами отрезки), и, следовательно, АВ=А₁В₁. Так как равные отрезки имеют равные длины, то наложение является отображением плоскости на себя, которое сохраняет расстояния, то есть любое наложение является движением плоскости.

Теорема

Доказательство

Дано: движение , АВС отображается в А₁В₁С₁, АВС=А₁В₁С₁

Доказать: движение — наложение

Доказательство:

Так как АВС=А₁В₁С₁ , то по определению существует наложение , при котором точки А, В и С отображаются в точки А₁, В₁ и С₁ соответственно. Докажем, что совпадает с .

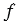
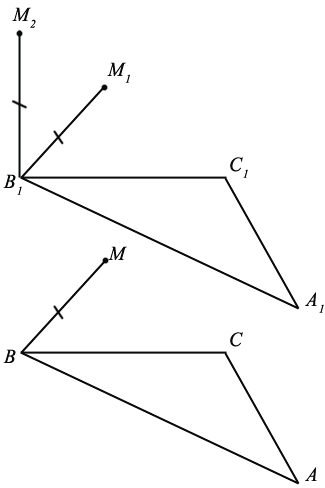
Предположим обратное. Тогда найдется хотя бы одна точка М, которая при движении отображается в точку М₁, а при наложении отображается в другую точку М₂. При отображениях и сохраняются расстояния, поэтому ВМ=В₁М₁, ВМ=В₁М₂, отсюда В₁М₁=В₂М₂, то есть точка В₁ равноудалена от точек М₁ и М₂.

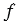
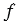
Аналогично можно доказать, что точки А₁ и С₁ равноудалены от точек М₁ и М₂. Следовательно, точки А₁, В₁, и С₁ лежат на серединном перпендикуляре к отрезку М₁М₂, но это не возможно, так как вершины А₁В₁С₁ не лежат на одной прямой. Значит, наше предположение неверно и отображение совпадает с , другими словами, движение является наложением. Теорема доказана.

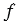
Следствие

Поделись с друзьями в социальных сетях:

Источник

Что значит «Сравнить фигуры наложением»?

Вот, в учебниках по геометрии пишут, что фигуры (например отрезок) можно сравнивать путём наложения отрезков друг на друга. Но как это делать ни в одном не написано, нифига не понятно, что это означает.

Вот, я взял линейку, построил на листе два отрезка, и каким образом я буду их накладывать теперь друг на друга, чтобы узнать равны ли они? Мне, что, вырезать их надо будет, чтобы наложить друг на друга?

Площадь фигуры «круг обрезаный синусоидой»
Доброго времени суток уважаемые форумчане. Помогите решить задачку. Даже не задачку, Просто нужна.

Что значит «реактивная» и «активная» составляющие для ЭДС?
Здравствуйте. У меня в задании дана ЭДС 130 В / 50 Гц. Как определить её активную и реактивные.

Что значит «%d %d\n» в функции вывода в файл fprintf(f, «%d %d\n», i, j);
Что значит «%d %d\n» в функции вывода в файл fprintf(f, «%d %d\n», i, j); Запутался, объясните.

В учебниках или конкретно в. как его? Атанасяне?

Как не написано, должно быть определение. По идее, это вид движения (изометрического аффинного преобразования).

Бумага — это такое вещество из длинных молекул, которые состоят из атомов, находящихся в тепловом движении. Когда по бумаге проводят карандашом, на ней остаётся след — слои кристаллической решётки углерода. Молекулы воздуха стучатся об это хозяйство, что-то застревает, какие-то атомы, наоборот, улетают с поверхности. Циркуль — тоже конструкция из атомов; это кажется, что он полированный, а так он весьма себе бугристый. Кроме прочего, ещё и химические реации идут — окисление в атмосфере.

Вы по-прежнему думаете, что это имеет отношение к геометрическим абстракциям?

Источник