Что такое наложение в математике
Как сравнить два отрезка: способы и примеры

Способы сравнения двух отрезков
В геометрии две фигуры, имеющие одинаковый размер и форму, называются равными. Сравнение фигур дает возможность сказать, одинаковы ли они. Одним из способов является наложение. Если фигуры удается совместить наложением, они считаются равными.
Сравнить фигуры — значит, определить, которая из них длиннее или короче. Ответ должен быть определенным, нельзя сказать, что один отрезок длиннее или равен второму. В математике такой ответ неправилен, его можно приравнять к отсутствию ответа.
Записывают результат сравнения с помощью знаков больше, меньше и знака равенство (>; АБ.
Сравнивать фигуры можно разными способами, выбор которых зависит от возможностей или условий:
Лучше всего, если они различаются по длине визуально, и, просто посмотрев на них, вы можете сказать, который длиннее. Но так бывает не всегда.
Измерение длины
Самый простой способ — измерение. Для этого можно использовать линейку, просто измерив длину отрезка, мы поймем, который из них длиннее. Если нет линейки, но они начерчены на листе в клетку, для измерения их длин можно посчитать клетки. В одном сантиметре две клетки. Это метод сравнения измерением длин, но есть еще метод сравнения наложением.
Обратите внимание: что такое луч в геометрии.
Наложение друг на друга
Как происходит совмещение АБ и ВГ:
Сравнение в координатной сетке
Допустим, что у нас есть два отрезка, координаты которых мы знаем — а (Х1, Y1; Х2, Y2) и b (Х3, Y3; X4, Y4).
Первое, что нужно сделать — придать координатам числовые значения:
Da = √ ((-7 — 3) ² + (4 — (-4)) ²) = √ (-10 ² + 8 ²) = √ 100 + 64 = √ 164
Db = √ ((-3 — 0) ² + (-5 — (-3)) ²) = √ (-3 ² + (-8) ²) = √ (9+ 64) = √ 73
√ 164 > √ 73, значит, Da > Db.
Также можно сравнить отрезки, находящиеся в трехмерной системе координат, надо учитывать не две, а три координаты каждого из них.
Примеры
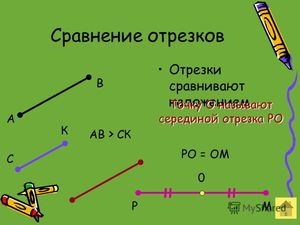
Чтобы узнать, равны они или нет, просто приложим их друг к другу так, чтобы их «начала» были в одной точке, то есть совместим точки, А и В.
Если мы видим, что АБ получается частью ВГ, значит, он меньше, то есть АБ 2, значит, CD>AB, то есть отрезок CD длиннее AB.
Наложения и движения
Напомним, что в нашем курсе геометрии равенство фигур определяется с помощью наложений. Мы говорим, что фигура Ф равна фигуре Фп если фигуру Ф можно совместить наложением с фигурой Ф1. Понятие наложения в нашем курсе относится к основным понятиям геометрии, поэтому определение наложения не даётся. Под наложением фигуры Ф на фигуру Ф1 мы понимаем некоторое отображение фигуры Ф на фигуру Ф1 Более того, мы считаем, что при этом не только точки фигуры Ф, но и любая точка плоскости отображается в определённую точку плоскости, т. е. наложение — это отображение плоскости на себя.
Однако не всякое отображение плоскости на себя мы называем наложением. Наложения — это такие отображения плоскости на себя, которые обладают свойствами, выраженными в аксиомах (см. приложение 1, аксиомы 7—13). Эти аксиомы позволяют доказать все те свойства наложений, которые мы себе представляем наглядно и которыми пользуемся при доказательстве теорем и решении задач. Докажем, например, что при наложении различные точки отображаются в различные точки.
В самом деле, предположим, что это не так, т. е. при некотором наложении какие-то две точки А и В отображаются в одну и ту же точку С. Тогда фигура Ф1, состоящая из точек А и В, равна фигуре Ф2, состоящей из одной точки С. Отсюда следует, что Ф2 = Ф1 (аксиома 12), т. е. при некотором наложении фигура Ф2 отображается в фигуру Ф1. Но это невозможно, так как наложение — это отображение, а при любом отображении точке С ставится в соответствие только одна точка плоскости.
Из доказанного утверждения следует, что при наложении отрезок отображается на равный ему отрезок. Действительно, пусть при наложении концы А и В отрезка АВ отображаются в точки А1 и В1. Тогда отрезок АВ отображается на отрезок А1В1 (аксиома 7), и, следовательно, отрезок АВ равен отрезку А1В1. Так как равные отрезки имеют равные длины, то наложение является отображением плоскости на себя, сохраняющим расстояния, т. е. любое наложение является движением плоскости.
Наложения и движения
При наложении различные точки отображаются в различные точки.
Доказательство:
Из этого утверждения мы можем сделать вывод, что при наложении отрезок отображается на равный ему отрезок. Пусть при наложении концы А и В отрезка АВ отображаются в точки А1 и В1. Тогда отрезок АВ отображается на отрезок А1В1 (т.к. согласно аксиоме, если при наложении совмещаются концы двух отрезков, то совмещаются и сами отрезки), и, следовательно, АВ=А1В1. Так как равные отрезки имеют равные длины, то наложение является отображением плоскости на себя, которое сохраняет расстояния, то есть любое наложение является движением плоскости.
Теорема
| Любое движение является наложением. |
Доказательство
Дано: движение 




Доказать: движение 
Доказательство:
Так как 


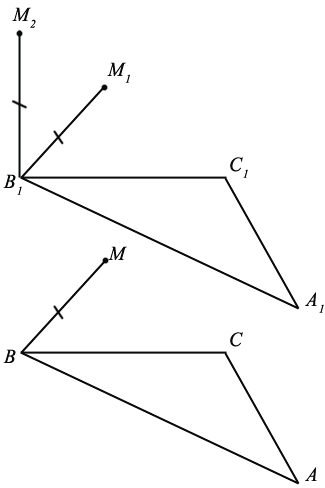
Предположим обратное. Тогда найдется хотя бы одна точка М, которая при движении 
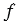

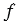
Аналогично можно доказать, что точки А1 и С1 равноудалены от точек М1 и М2. Следовательно, точки А1, В1, и С1 лежат на серединном перпендикуляре к отрезку М1М2, но это не возможно, так как вершины 

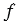

Следствие
| При движении любая фигура отображается на равную ей фигуру. |
Поделись с друзьями в социальных сетях:
Что такое наложение в математике
| Произведения | 4 911 |
| Биографии | 2 004 |
| Библиографии | 10 251 |
| Словари | 161 |
| Словарные статьи | 1 244 714 |
| Автор | Мордухай-Болтовской Д.Д. |  |
| Название | Философия. Психология. Математика | |
| Год издания | 1998 | |
| Раздел | Книги | |
| Рейтинг | 0.39 из 10.00 | |
| Zip архив | скачать (1 674 Кб) | |
 Поиск по произведению Поиск по произведению |
Из истории метода наложения в элементарной геометрии
§ 1. Евклид и Лежандр.
Понятие о сущности математического доказательства подверглось через толщ>’ веков глубочайшему изменению, хотя это изменение и ие было заметно самим исследователям так, как не заметно старение стареющему человеку. То. что Лежандр считает доказательством, не могло быть признано за доказательство Евклидом и, с другой стороны, Лежандр ие мог начать свои «Элементы» с построения равностороннего треугольника, как это делает Евклид.
Не следует думать, что Лежандр 2 в своих упрощенных доказательствах додумался до тех более простых доказательств, которые ускользнули от Евклида. Евклид, очень может быть, знал эти доказательства, но отверг их как негодные, как находящиеся в решительном противоречии с его взглядами на доказательство. Почему ему не поступать так, как Лежандр, при доказательстве основного свойства равнобедренного треугольника, состоящего в том, что углы, противолежащие равным сторонам, равны?
Между тем, Евклид излагает другое, более сложное доказательство (так называемое elefuga ). Ответим: потому, что Евклид признавал существование только тех объектов, которые могут быть построены.
И только благодаря коренному изменению требований, предъявляемых к доказательству, Лежандр получает возможность упростить геометрическую систему и перевернуть порядок теорем.
Он начинает с положения:
«Если две стороны одного треугольника равны соответственно сторонам другого и если в то же время угол между первыми более угла, заключенного между вторыми, то третья сторона первого будет больше третьей стороны второго».
Но это только 24-я теорема I книги «Начал» Евклида, т.е. весьма отдаленная от начала теорема, которая доказывается на основании третьего случая конгруэнтности треугольников.
Для доказательства того, что
АС = GH I также hBC > FH ZBAC > ZFGH
руэнтностиХпроводггг биссек трису АЕ угла няет Е с D
У Клавия мы находим разновидность этого метода, чуждую Евклиду.
На первый взгляд может показаться, что если Аристотель и Евклид не могли бы признать наложение с переносом идеального треугольника, то такая операция могла бы оказаться во вкусе Платона, объектиро- вавшсго идеи и геометрические формы. Видимо, Цейтен 23 так и думает, Он говорит, что математические истины древним представлялись или как теоремы, или как проблемы. Первая точка зрения поддерживалась последователями Платона, думавшими, что проблема только устанавливает то, что уже предварительно существовало, независимо оттого факта, строится оно или нет, более того, построить что-либо, например, разносторонний треугольник, можно только потому, что идея равносторнннего треугольника имеет существование, предваряющее всякое построение.
В «Началах» Евклида Цейтен видит примирение этих точек зрения, Но для того, чтобы Платон и его ученики понимали геометрию так. как понимал ее, например, Декарт, для этого мало ему было признать идеальное существование геометрических фигур в каком-то другом мире, (тотго^ уог|то? ) и том мире, бледным отражением или тенью которого является настоящий. Необходимо было признать их в этом мире, в самих вещах. При методе наложения переносится не платоновский идеальный треугольник из другого мира, а на этот, первый тот второй; треугольник и не материальный, а идеальный, который, так сказать, живет в первом.
§ 4. Рационалисты против метода наложения.
С развитием рационалистической 25 логики и гносеологии, философы и математики XVII века становятся в явно враждебное отношение к этому методу доказательства. Этот метод, по их мнению, убеждает с помощью обращения к чувствам, а не к чистому разуму, который только один и является судьей.
AB = A ‘ B ‘, AC = A ‘ C ‘, ZBAC = ZB ‘ A ‘ C ‘
то всегда имеют место и конгруэнции
Еще в XVI веке делают опыты построения доказательств равенства треугольников без метода наложения.
Доказательство Кандалы 30 первого случая кошруэнтности треугольников, критикуемое Савплнем, состоит в следующем. Так как по предпо-
расстояния точек ( а и р ) и (5 и s ). ( Здесь Кандала берет определение прямых Прокла, которое последний считает эквивалентным евклвдовскому, а именно, что прямая линия между двумя точками равна их расстоянию).
Поэтому и остальные элементы равны, т.е. углы |3 и У соответственно равны s iiC 15 .
Не будем останавливаться на критике Савилия, смотрящего на это доказательство как на неубедительное, как основанное на положениях не более очевидных, чем доказуемое. Заметим только, что из защиты Сави- лия метода наложения видно, что при выработанной схоластическим реализмом объективации геометрических форм операция наложения сперва не представляется недопустимой. Идеальный треугольник переносится ие в действительности, так как его нельзя взять в руки, но только в воображении.
По Савплию,» это вполне возможно в теореме (но не в проблеме), так как в теореме не требуеся никакого действия, требуется только обнаружить истинное или ложное, и нет ничего ложного в том перенесении, которое делаем только одним воображением, а не руками или операцией, употребляемой при построении.
К невозможности перенесения приводит лишь дальнейшее размышление об идеальных объектах, которые обявляются не только не ощущаемыми, но в собственном смысле и не воображаемыми.
Все действия над воображаемыми фигурами представляются как действия не над идеальными фигурами, а образами материальных тел.
Геометрия, наконец, объявляется возможной без чертежа не только конкретного, но и воображаемого.
Философско-математические идеи XVI века.
Очень может быть, что в нарисованной мной картине этого отдаленного прошлого ие все правильно, но и у хорошего художника сходство в редких случаях с первого раза полное. Может быть мне, а может быть другим удастся в будущем замазать неправильно уловленные черты другими, приближающими к большему сходству.
Но я в се таки льщу себя, что и мои несовершенный очерк может оказаться полезным.
В заключение считаю необходимым выразить свою благодарность приват-доценту Императорского Московского Университета В.В. Бобыни- иу за ряд для меня полезных советов и указаний, библиотекарю того лее университета и помощнику его за любезную помощь при моей работе в библиотеке этого университета, Факультету и Совету Императорского Варшавского Университета за средства к напечатанию этой работы.
Проф. Д. Мордухай-Болтовской. г. Ростов-на-Дону. Октябрь 1916 г.
§ 1. Общая характеристика мысли XVI века.
Нельзя отрицать своеобразной физиономии XVI века, во многом отличающейся как от средневековья, так и от рационализма XVII века. Это эпоха борьбы с авторитетом, эпоха юности, возрождающейся от гнета научной мысли.
Чисто юношеская жажда знания заставляет ее устремляться в те области, доступ в которые в позднейшее время рационалистического отрезвления был окончательно закрыт.
Ум, который привык верить, перестав верить в то, во что он раньше горячо верил, ищет новой пищи для своей веры. Этой наивной веры уже нет у мыслителя XVII века, который, сохранив только пламенную веру в разум, старается всю вселеную заключить в бесспорно узкие для нее рамки геометрической логики.
Что характерно для математиков XVI века, это недостаток их artis demonstrandi ; они хороши, когда ищут новые методы, ибо эти методы их оказываются правильными и могут быть обоснованы, но сами они не могут, да и не особенно стараются их обосновать. Как сын остается похожим на отца, хотя бы находился с ним в самых враждебных отношенаях, так и рамизм XVI века, враг схоластики, похож на схоластику, из которой он в конце концов вышел. Ваддингтон» указывает три принципа, характеризующие рамизм: право разума на свободное исследование, борьба с крайностями средних веков и упрощение наук употреблением правильных метод.
Но это, конечно, характеристика деятельности, а не мировоззрения рамизма.
С последней точки зрения, ои не далеко от схоластики. Естественная логика, которая им противополагается логике Аристотеля, представляет ту ле е, но только несколько видоизмененную логику Аристотеля, изменение которой в то время казалось огромным, а в настоящее время ничтожным. Метод исследования остается по существу схоластическим.
Зачаткам новой философ™, говорит Виндельбанд 7 свойственна инстинктивная оппозиция против «схоластики» и наивное непонимание общей зависимости, в которой сами они находятся от какой-либо ее традиции».
§ 2. Эволюция иерархического принципа в онтологии.
Этот идеал, конечно, создался средневековым реализмом, видевшим в возрастающей общности классов, возвышающиеся степени существования, так что genus generalissiuium является вместе с тем и одаренным наибольшей полнотой существования.
Легко отсюда видим, какое значение в глазах средневекового мыслителя имело определение.
В высокой степени интересно проследить эволюцию основного принципа, лежащего в основе иерархической лестницы существ. Вне сомнения, иерархические идеи пускают свои корни в политеистическое мировоззрение еще самых низших ступеней развития человека.
Этот живой н красочный мир Платона, в атмосфере схоластики, обращается в бесцветный и безжизненный мир абстракции, в восходящую до пустого понятия бытия иерархию теряющих в своем содержании и вы-игривающих в объеме соподчиненных друг другу универсалий, за которыми оставались, как за их предками, постепенно возвышающиеся степени реальности.
С окончательным падением реализма в ХШ- XIV вв. поколебалось и основание указанной выше иерархии, ибо большей общности уже перестала отвечать большая степень реальности.
Но в XV и XVI веках старались влить новое вино в старые меха, живую вселенную, которая открылась им, освобожденным от средневекового тумана глазам, включить в выработанные схоластикой омертвелые формы.
XVI век стоит уже недалеко оттого момента, когда гений Декарта разбил эти формы.
Наряду с логикой классов схоластиков, у рационалистов выступает логика отношений. Лежащие в основе науки аксиомы говорят не столько об отнесении данного объекта или вида к определенному классу, сколько о взаимоотношении различных объектов.
Глазам рационалиста вся вселенная представляется, как ряд взаимоотношений, вытекающих из небольшого числа аксиом, относящихся к простейшим отношениям.
§3. Логические идеи Рамуса.
Математика XVI века преимущественно интересуют задачи. Но при решении их он не проявляет критического отношения к постановке проблемы, ни к ее решению.
Так, например, вместо того, чтобы делить треугольники на прямоугольные, косоугольные и остроугольные, молено их делить теперь на прямоугольные и непрямоугольные, а затем последние на косоугольные и остроугольные.
Именно эта схема должна была оказаться боль ше всего по сердцу концептуалисту. л
С концептуалистической точки зрения, как А так и не А суть только модусы мыслящего духа и обладают, так сказать, равными правами. Поэтому для концептуалиста является весьма естественным остановиться именно на рамической дихотомной схеме, правильность и простота строения которой дает уже ие онтологическую, а логическую проблему.
Но позже, поиски естественно-научных методов увенчиваются учением об опытной индукции Фрэнсиса Бэкона и переходом от жившего методами прошлого и ищущего методов будущего гуманитарного периода, к периоду естественно-научиому,
Рамус выступает не только против Аристотеля, но и против Евклида. Он не ограничивается одной критикой, он старается дать образец исправленаых «Начал».
«Если бы, говорит Рамус, Евклид был бы настолько логиком, насколько был математиком, то на вопрос Птоломея: «Не существует ли к математической философии более короткого пути, чем тот, который дают «Начала», я думаю, никогда не ответил бы, что нет такого царственного пути.
Ибо царственный путь может быть ие только более кратким, более планомерным ( planior ) и более широким ( amplior ), но при этом, необходим логический аппарат, легкий для познания и трудный для осуществления. Путь можно исправить, но для этого необходим труд больший, чем это кажется».
Рамус вполне сознает, гак трудно вогнать геометрию в узкие схоластические рамки аристотеле-рамической логики. Задача им поставленная много трудней, чем задачи рационалиста Арно, эмпирика Бертрана или логистов Саньо и д’Овидио. «
Конечно, для Рамуса самым важным в геометрии являются определения, а за ними [логический] план геометрии.
В чем главный недостаток Евклида?
В том, что он идет от частного к общему вместо того, чтобы идти от общего к частному. С точки зрения Рамуса и его современников именно в определении происходит наиболее важный акт.
Мы скажем: «Да не все ли равно, как определять параллельные;’ лишь бы все, что затем следует [из определения], было бы правильно выведено».
«Нет!», возразил бы Рамус,. «математика имеет целью, как всякая другая наука, исследование свойств вещей, которые некоторым образом уже даны до начала математического исследования».
Концептуализм перевел идеи из внешнего мира в наш дух, но не перестал на них смотреть, как на неподвижные и неизменные сущности, изначально обретающиеся в нем, но не органически из него развивающиеся.
Последний взгляд был достоянием отдаленного будущего.
§4. Рамус о геометрических определениях.
Обратимся к геометрии Рамуса. Возьмем определение круга. Здесь и в настоящее время существует некоторая словесная путаница; «круг» употребляется и в смысле кривой, и в смысле площади, ограниченной этой кривой согласно 15-му определению I кн. «Начал» 21 : «Круг есть плоская фигура, содержимая одной линией, называемой окружностью, к которой все прямые, исходящие от одной из точек, внутрь сей фигуры лежащих, взаимно равны».
И Рамус говорит не только о центре круга, он говорит вообще о центрах.
Каждый из нас отнесет к одному классу и центр квадрата, и центр круга.
Все это центры- симметрии, о которых мы получаем идею много раньше, чем в состоянии облечь ее в научное определение.
Евклид, если и имел эту идею, то все-таки выключил ее из своих «Начал», так как она ему оказалась не нужной для выводимой цепи положений. Рамус же ие мог обойти этот обобщенный центр при присущем тому времени стремлении к построению иерархий объемлющих друг друга классов.
Определение центра у него [следующее]:
Centrum est punctum in figura medium.
Центр [есть] середина фигуры.
Т.е. им предполагается, что то, что нужно считать серединой (в тех, конечно, фигурах, где эта середина есть) каждый знает, и снабжает эту точку названием: центр.
Радиус [по Рамусу, ес п>1 не только у круга.
Радиус [есть] у всякой фигуры, имеющей центр. Это- прямая, идущая от центра к периметру (отсюда выводится, что центр [находится] в пересечении диаметров).
Angulus est lineatum in communi sectione terminorum.
Угол есть линеатум в общем сечении членов.
Параллелизм прямых подводится под общее понятие параллелизма линий (как прямых, так и кривых). Параллельными являются ие только прямые, но, например, два концентричных круга (или, вернее, окружности).
Под род параллельных линий подводятся два вида: параллельные кривые и параллельные прямые. Определять следует не «прямые параллельные», а вообще параллельные линии, из какового класса «прямые параллельные» выделяются благодаря признаку прямизны. Но, как основательно замечает Рамус, та идея о параллелизме, которую мы находим в себе, менее всего характеризуется несхождением прямых. Кривые не параллельные могут не сходиться, какова, например, конхоида или гипербола с их ассим-птомами.
При этом свойство, что две линии, паралельные каждая третьей, параллельны между собой, распространяется и на случай кривых параллельных.
[У Рамуса] определяется не высота треугольника и затем высота призмы и т.д., а высота вообще.
Altitudo est perpendicuiaris a vertice figurae ad basin.
«Когда прямая, поставленная на другую прямую, делает смежные углы взаимно равными, то каждый из равных углов называется прямым; а поставленная прямая называется перпендикулярной или отвесной к той, на которую поставлена».
«Прямые взаимно-перпендикулярны, если одна, падая на другую, равномерно между ними лежит ( aequaliterinterjacet )».
такая же как В, так что отношение перпендикулярности [по Рамусу] является несимметричным: радиус перпен дикулярен к окружности, но окружность не перпендику- ( 0 лярна к радиусу.
Для того, чтобы подвести подобие окружностей под общее опредление подобия, которое берется из
евклидового определения прямолинейных подобных
Онне вооружается против евклидовых генетических определений, но выставляет в комментариях другие, не евклидова типа определения.
Евклид дает для шара, определение совсем не то, которое соответствует приведенному выше евклидову определению круга.
Такое определение дает Клавий в своих комментариях в дополнение к евклидову:
Sphaera est figura solida una superficie coraprehensa ad quam ab im o puncto eo rora quae intra figuram sunt posita cadentes rectae liniae inter se sunt aequales.
Не трудно видеть, отчего Евклид не мог дать это определение, а дал другое:
14 опред. XI книги «Начал»:
«Шар есть тело, производимое через обращение полукружия на неподвижном его поперечнике, пока оное опять восставится там, откуда началось его обращение».
В самом деле, Евклиду при определении Клавия, пришлось бы, как и к приведенному выше определению круга приставить постулат о возможности описания данным радиусом шара 1 «,
Средневековое мышление положило свой отпечаток на понятие о геометрическом существовании, которое подверглось незаметной для самих математиков метаморфозе.
? 5. Порядок геометрии по Рамусу
В «Началах» Евклида все аксиомы стянуты к началу I книги.
Вспомним эпоху Евклида, вспомним, что «Начала» Евклида являлись своего рода крепостью, которая должна была быть готова выдержать тяжелые орудия софистов.
Не трудно уяснить себе стратегические приемы софистов.
Их должно было быть немного и с ними следовало, как можно скорее покончить.
Без сомнения, для софиста было в высокой степени выгодно делать это не в начале, а потом, при ходе дальнейшего изложения или спора требовать от собеседника или противника признания не высказанных раньше аксиом.
Вне сомнения, что чем позиция его противника становилась опасней и спор казался ближе к окончанию для противника неблагоприятному, тем менее последний становился чувствительнее к этим общепризнанным истинам.
Вся евклидова логика, как и логика Сократа и Платона вышла из софистической логики совершенно так же, как логика Рамуса из схоластической.
Определения, в противоположность аксиомам оказываются распределенными между различными книгами.
Нужные для данной книги определения помещаются в начале ее.
Собственно говоря, и определение тоже следовало помещать в начале книги. Вероятно, так это и делалось бы, если бы «Начала» были меньше. Но в таком большом труде, как «Начала» Евклида это было бы уже невозможно, так как читатель не был бы в состоянии удержать в своей памяти всю ту массу необходимых определений, которые выставляет Евклид.
Такой порядок аксиом и определений в настоящее время является недопустимым. Система определений должна постепенно развертываться с цепью теорем.
Если мы определяем А совокупностью признаков: а, Ь, с. то мы должны предварительно доказать совместность этих признаков а, Ь, с. что возможно сделать только протянув уже часть цепи друг за другом следующих положений.
Необходимость оправдания определений некоторыми начала сознаваться еще в XVI i веке.
Но проблема обоснования геометрических истин, вплоть до второй половины XIX века, сводилась к выводу положений из системы очевидных категорических суждений.
Если к категорическим суждениям присоединить условные, то дело изменится.
За аксиому можно было бы признать положение: «Если имеет место А, то также имеет место и В».
Но наличность А может быть не очевидной, и приходится доказывать ее из других уже очевидных категорических суждений. В таком случае аксиомы уже рассеиваются по всей сети доказываемых положений.
Рамус тоже вооружается против евклидова порядка, но, исходя из совершенно иных, нам совершенно чуждых идей.
«Природа, говорит Рамус, ие создает лес таким образом, что производит сразу для всех деревьев корни, а затем к ним стволы; архитектор не будет строить город таким образом, что для всех домов сперва воздви- иет фундаменты, а затем займется самими постройками.
. Евклид должен определить треугольник там, где он начинает теорию треугольников, четырехугольник там, где начинает говорить о четырехугольнике».
Но Клейн забывает сказать главное: еще выше практических интересов у Рамуса стоят схоластические интересы, построение delineatio 34 геометрии, родословного дерева геометрических классов с удовлетворяющими его логике определениями.
Таково определение contiouilas (непрерывности или, вернее, непрерывного геометрического образа), объемлющего собой виды линий, поверхности, тела.
«Contimiitas est indiscrecio lerminorura cum terminandi potentia».
Angulus est continuarum in contiuutatis termine convencium.
Вот родословная классов, которую можно извлечь из геометрии Рамуса.
Соответственно этой delineatio порядок геометрии Рамуса такой: сперва говорится о наиболее общем, о том, что такое величина ( magnitude ), о границах ее, о наложимости, как условии равенства. Затем о линиях вообще, об их перпендикулярности и параллельности, отнюдь не только прямых. От linea следует перейти к lineatuin и, прежде всего, к углам: исследовать условия равенства углов и различные виды углов.