Что такое направление вектора
Характеристики вектора: длина, направление, координаты
У любого вектора есть 2 главные характеристики:
Третья характеристика вектора – это его координаты.
Примечание:
Зная координаты вектора, можно найти его длину и направление. Поэтому, задавать информацию о векторе можно двояко: либо указав его длину и направление, либо его координаты.
Что такое координаты вектора
Координаты вектора – это длины его теней на осях координат (его проекции на оси).
Координаты вектора указывают так:
\( a_
\( a_
Координаты вектора можно получить из координат его начальной и конечной точек:
«координата вектора» = «конец» — «начало»
Пример:
\( A \left( 1;1 \right) \) — начальная точка,
\( B \left( 4;3 \right) \) — конечная точка,
\[ \overrightarrow
\[ \begin
Длина вектора (в чем измеряется, как посчитать)
Длину вектора (его модуль) обозначают так:
Как вычислить длину вектора по его координатам
Когда известны координаты вектора, его длину считают так:
\( a_
Для двухмерного вектора:
Для трехмерного вектора:
Как вычислить длину вектора с помощью рисунка
Если вектор нарисован на клетчатой бумаге, длину считаем так:
1). Если вектор лежит на линиях клеточек тетради:
— считаем количество клеточек.
Зная масштаб клеток, легко получить длину вектора – умножаем масштаб на количество клеток.
2). Если вектор не лежит вдоль линий:
— проводим вертикаль и горизонталь пунктиром.
\( \Delta x \) — горизонталь; \( \Delta y \) — вертикаль;
— затем применяем формулу:
Как указать направление вектора
Указать направление вектора можно с помощью его координат. Так как в его координатах уже содержится информация о длине и направлении вектора.
Бывает так, что координаты вектора неизвестны, а известна только лишь его длина. Тогда направление можно указать с помощью угла между вектором и какой-либо осью.
Для двумерного вектора
Если вектор двумерный, то для указания направления (см. рис. 10) можно использовать один из двух углов:
Словами указать направление вектора можно так:
Такой способ указания координат используют в полярной системе координат.
Для трехмерного вектора
Когда вектор располагается в трехмерном пространстве, чтобы указать, куда вектор направлен, используют два угла.
Такой способ указания координат используют в сферической системе координат.
Считаем Землю шаром. Расположим ее центр в начале трехмерной системы координат – точке (0 ; 0 ; 0).
Тогда координаты любой точки на поверхности планеты можно указать с помощью радиус-вектора этой точки.
Для указания сферических координат принято использовать:
Знакомимся с вектором
Основы линейной алгебры для тех, кого это миновало в универе.
Вы наверняка слышали много историй о программистах, которые учились в технических вузах, изучали высшую математику и теперь пользуются этими знаниями в программировании. И если кого-то это не коснулось, может быть ощущение, что он пропустил в жизни что-то важное.
Будем это исправлять. Попробуем разобрать некоторые базовые понятия из математики за пределами школьной программы. И заодно покажем, как оно связано с программированием и для каких задач полезно.
⚠️ Математики, помогайте. Мы тут многое упростили, поэтому будем рады увидеть ваши уточнения и замечания в комментариях.
Линейная алгебра
Есть математика: она изучает абстрактные объекты и их взаимосвязи. Благодаря математике мы знаем, что если сложить два объекта с ещё двумя такими же объектами, то получится четыре объекта. И неважно, что это были за объекты: яблоки, козы или ракеты. Математика берёт наш вещественный мир и изучает его более абстрактные свойства.
Внутри математики есть алгебра: если совсем примитивно, то в алгебре мы вместо чисел начинаем подставлять буквы и изучать ещё более абстрактные свойства объектов.
Внутри алгебры есть линейная алгебра — она изучает векторы, векторные пространства и другие абстрактные понятия, которые в целом относятся к некой упорядоченной информации. Например, координаты ракеты в космосе, биржевые котировки, расположение пикселей в изображении — всё это примеры упорядоченной информации, которую можно описывать векторами. И вот их изучает линейная алгебра.
В программировании линейная алгебра нужна в дата-сайенс, где из упорядоченной информации создаются алгоритмы машинного обучения.
Если представить линейную алгебру в виде дома, то вектор — это кирпич, из которого всё состоит. Сегодня разберёмся, что такое вектор и как его понимать.
Что такое вектор
Вы наверняка помните вектор из школьной программы — это такая стрелочка. Она направлена в пространство и измеряется двумя параметрами: длиной и направлением. Пока длина и направление не меняются, вектор может перемещаться в пространстве.
Физическое представление вектора: есть длина, направление и нет начальной точки отсчёта. Такой вектор можно как угодно двигать в пространстве
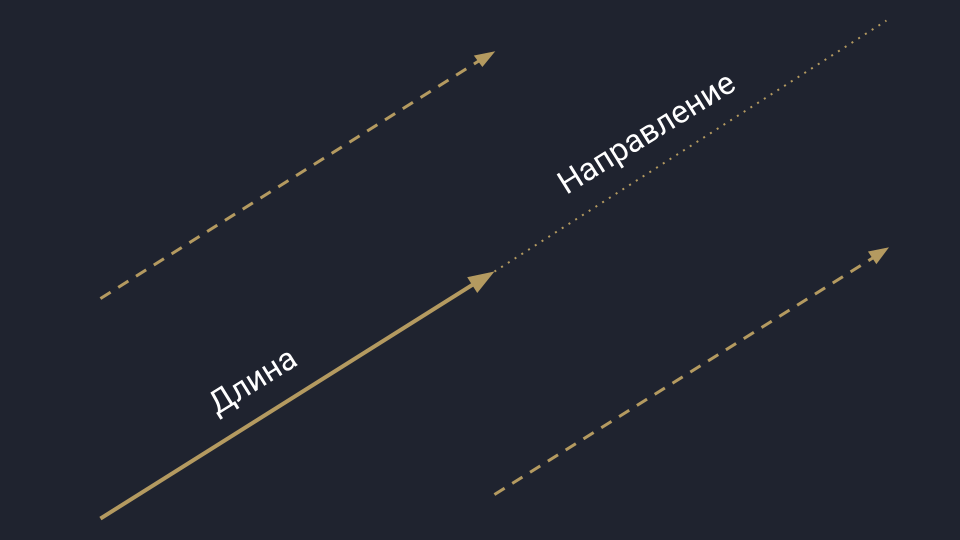
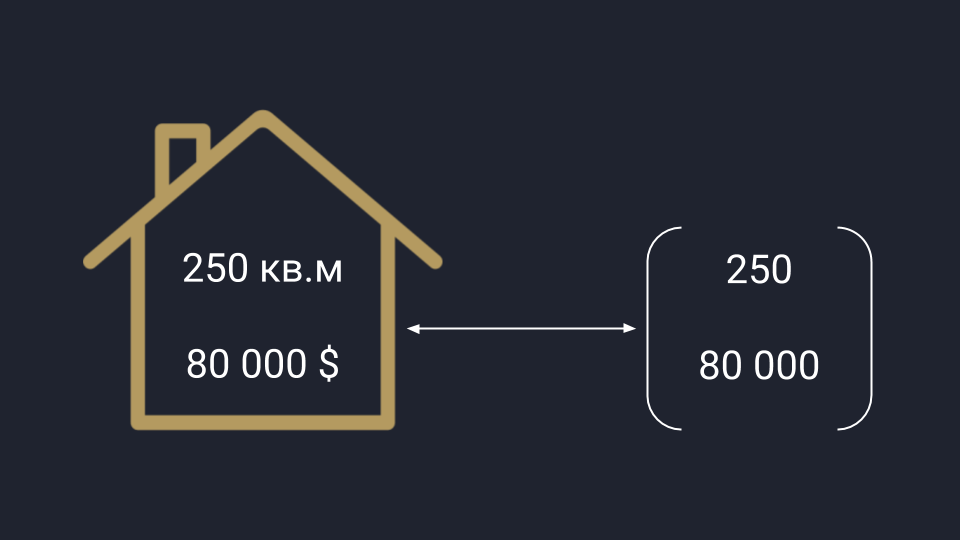
У аналитиков вектор представляется в виде упорядоченного списка чисел: это может быть любая информация, которую можно измерить и последовательно записать. Для примера возьмём рынок недвижимости, который нужно проанализировать по площади и цене домов — получаем вектор, где первая цифра отвечает за площадь, а вторая — за цену. Аналогично можно сортировать любые данные.
Аналитическое представление вектора: данные можно перевести в числа
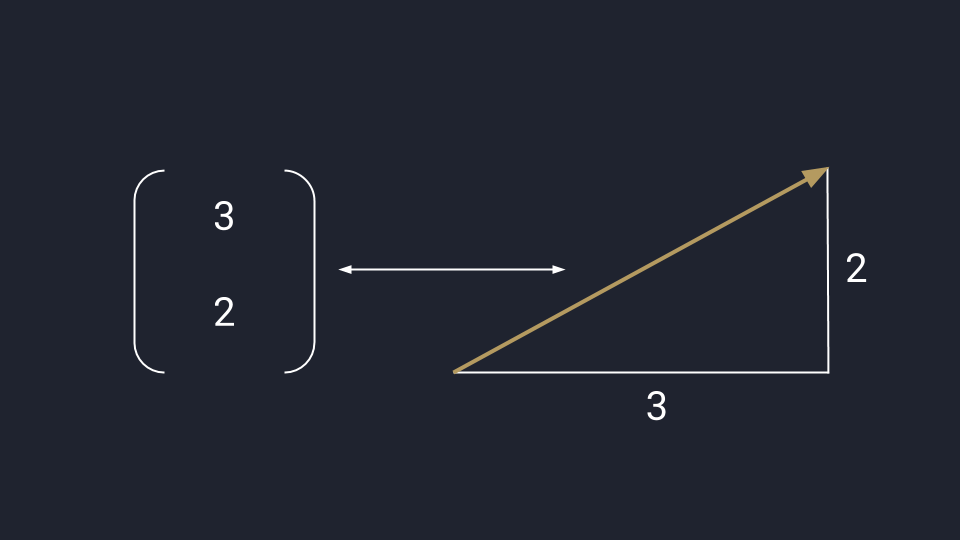
Математики обобщают оба подхода и считают вектор одновременно стрелкой и числом — это связанные понятия, перетекающие друг в друга в зависимости от задачи. В одних случаях удобней считать, а в других — показать всё графически. В обоих случаях перед нами вектор.
Математическое представление вектора: данные можно перевести в числа или график
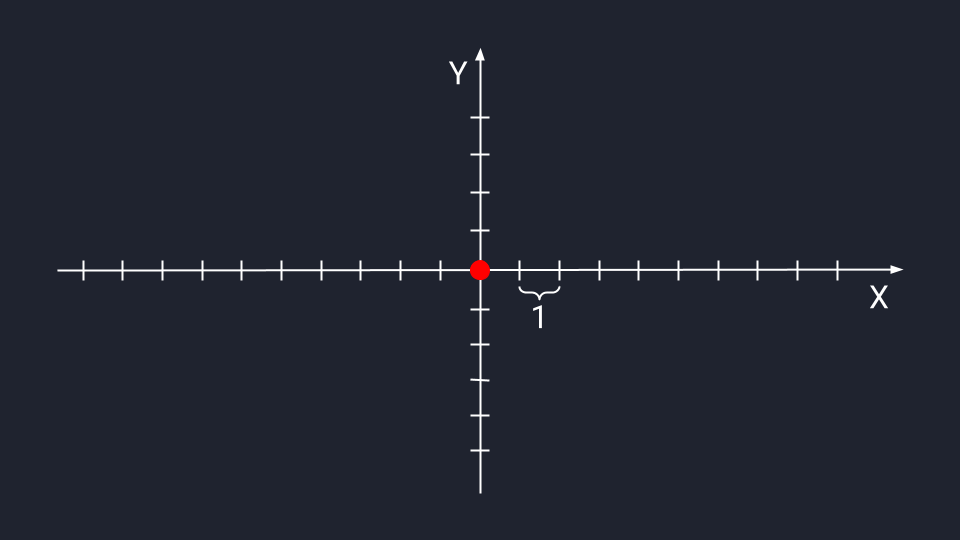
В дата-сайенс используется математическое представление вектора — программист может обработать данные и визуализировать результат. В отличие от физического представления, стрелки векторов в математике привязаны к системе координат Х и У — они не блуждают в пространстве, а исходят из нулевой точки.
Векторная система координат с базовыми осями Х и Y. Место их пересечения — начало координат и корень любого вектора. Засечки на осях — это отрезки одной длины, которые мы будем использовать для определения векторных координат
👉 Получается, вектор – это такой способ записывать, хранить и обрабатывать не одно число, а какое-то организованное множество чисел. Благодаря векторам мы можем представить это множество как единый объект и изучать его взаимодействие с другими объектами.
Например, можно взять много векторов с ценами на недвижимость, как-то их проанализировать, усреднить и обучить на них алгоритм. Без векторов это были бы просто «рассыпанные» данные, а с векторами — порядок.
Как записывать
Вектор можно записать в строку или в столбец. Для строчной записи вектор обозначают одной буквой, ставят над ней черту, открывают круглые скобки и через запятую записывают координаты вектора. Для записи в столбец координаты вектора нужно взять в круглые или квадратные скобки — допустим любой вариант.
Строгий порядок записи делает так, что каждый набор чисел создаёт только один вектор, а каждый вектор ассоциируется только с одним набором чисел. Это значит, что если у нас есть координаты вектора, то мы их не сможем перепутать.
Способы записи вектора
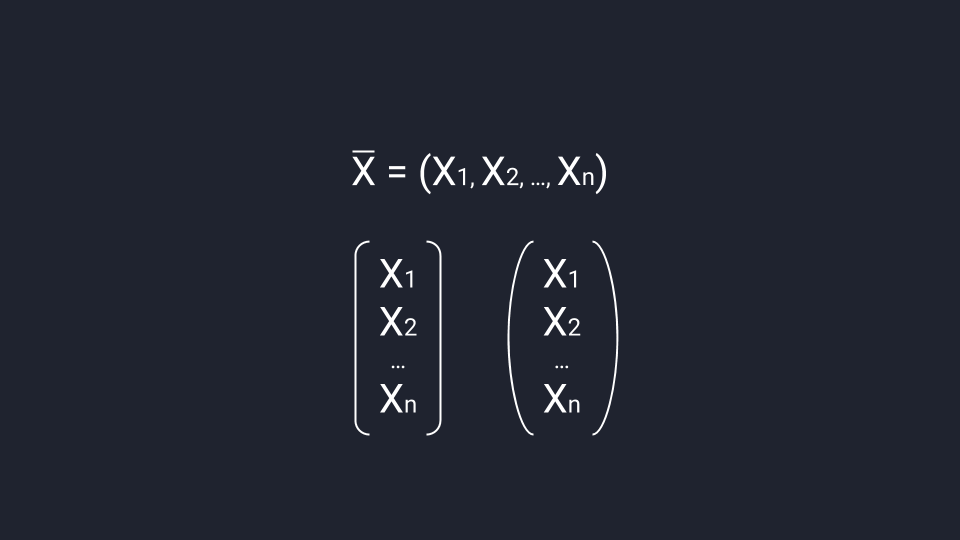
Скаляр
Помимо понятия вектора есть понятие скаляра. Скаляр — это просто одно число. Можно сказать, что скаляр — это вектор, который состоит из одной координаты.
Помните физику? Есть скалярные величины и есть векторные. Скалярные как бы описывают просто состояние, например, температуру. Векторные величины ещё и описывают направление.
Как изображать
Вектор из одного числа (скаляр) отображается в виде точки на числовой прямой.
Графическое представление скаляра. Записывается в круглых скобках
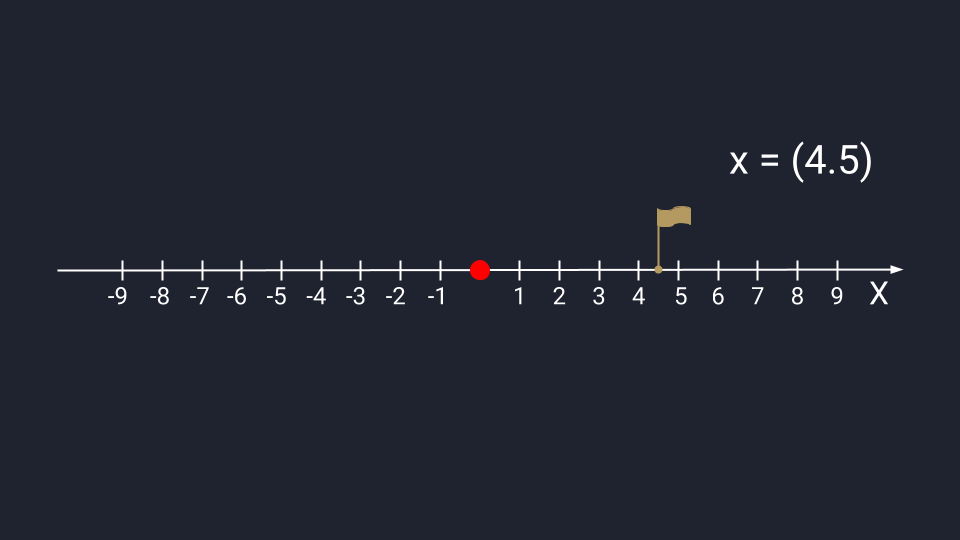
Вектор из двух чисел отображается в виде точки на плоскости осей Х и Y. Числа задают координаты вектора в пространстве — это такая инструкция, по которой нужно перемещаться от хвоста к стрелке вектора. Первое число показывает расстояние, которое нужно пройти вдоль оси Х; второе — расстояние по оси Y. Положительные числа на оси Х обозначают движение вправо; отрицательные — влево. Положительные числа на оси Y — идём вверх; отрицательные — вниз.
Представим вектор с числами −5 и 4. Для поиска нужной точки нам необходимо пройти влево пять шагов по оси Х, а затем подняться на четыре этажа по оси Y.
Графическое представление числового вектора в двух измерениях
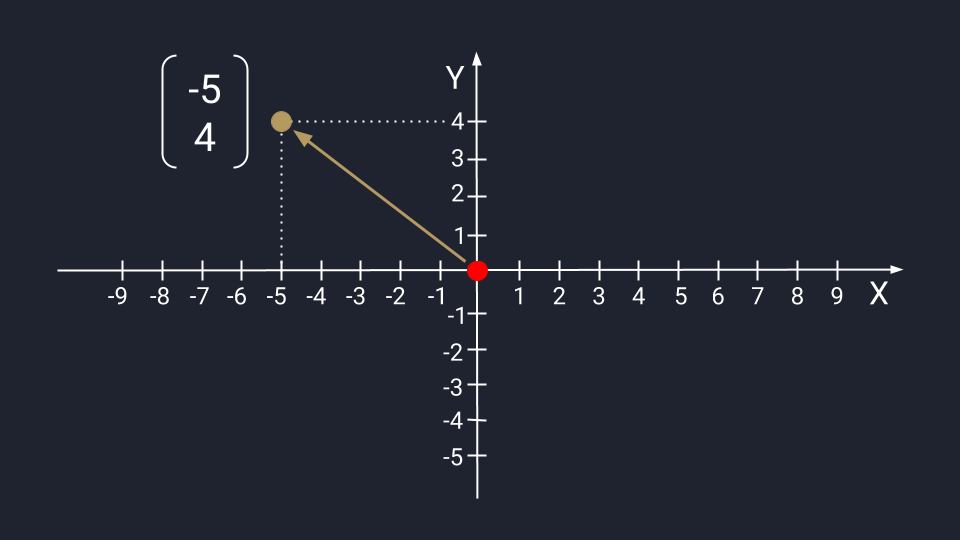
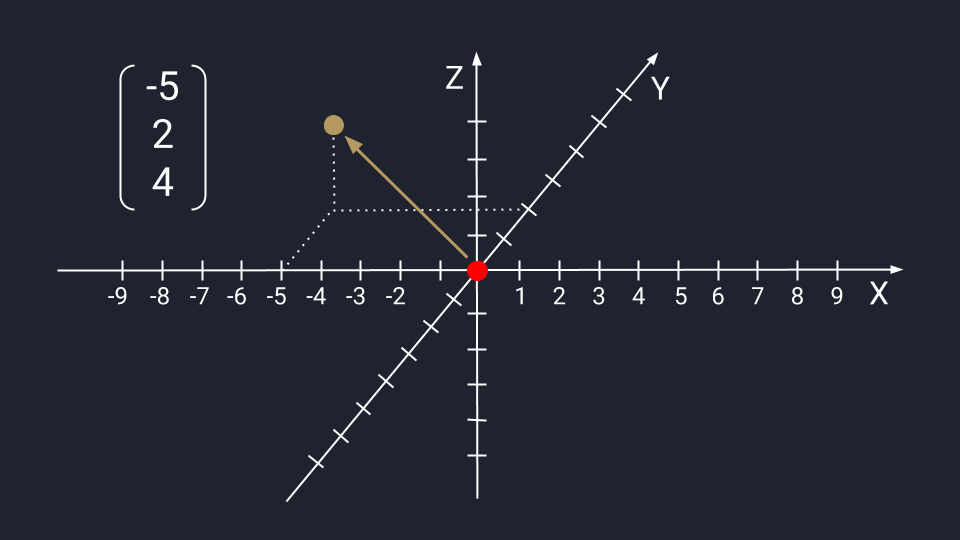
Вектор из трёх чисел отображается в виде точки на плоскости осей Х, Y и Z. Ось Z проводится перпендикулярно осям Х и У — это трёхмерное измерение, где вектор с упорядоченным триплетом чисел: первые два числа указывают на движение по осям Х и У, третье — куда нужно двигаться вдоль оси Z. Каждый триплет создаёт уникальный вектор в пространстве, а у каждого вектора есть только один триплет.
Если вектор состоит из четырёх и более чисел, то в теории он строится по похожему принципу: вы берёте координаты, строите N-мерное пространство и находите нужную точку. Это сложно представить и для обучения не понадобится.
Графическое представление числового вектора в трёх измерениях. Для примера мы взяли координаты −5, 2, 4
Помните, что все эти записи и изображения с точки зрения алгебры не имеют отношения к нашему реальному трёхмерному пространству. Вектор — это просто какое-то количество абстрактных чисел, собранных в строгом порядке. Вектору неважно, сколько там чисел и как их изображают люди. Мы же их изображаем просто для наглядности и удобства.
Например, в векторе спокойно может быть 99 координат. Для его изображения нам понадобилось бы 99 измерений, что очень проблематично на бумаге. Но с точки зрения вектора это не проблема: перемножать и складывать векторы из двух координат можно так же, как и векторы из 9999999 координат, принципы те же.
И зачем нам это всё
Вектор — это «кирпичик», из которого строится дата-сайенс и машинное обучение. Например:
Кроме того, векторы используются в компьютерной графике, работе со звуком, инженерном и просто любом вычислительном софте.
И давайте помнить, что вектор — это не какая-то сложная абстрактная штука, а просто сумка, в которой лежат числа в определённом порядке. То, что мы называем это вектором, — просто нюанс терминологии.
Что дальше
В следующий раз разберём операции с векторами. Пока мы готовим материал — рекомендуем почитать интервью с Анастасией Никулиной. Анастасия ведёт ютуб-канал по дата-сайнс и работает сеньором дата-сайентистом в Росбанке.
Вектор, его направление и длина
Вектором называется упорядоченная пара точек. Первая точка называется началом вектора, вторая — концом вектора. Расстояние между началом и концом вектора называется его длиной. Вектор, начало и конец которого совпадают, называется нулевым, его длина равна нулю. Если длина вектора положительна, то его называют ненулевым. Ненулевой вектор можно определить также как направленный отрезок, т.е. отрезок, у которого одна из ограничивающих его точек считается первой (началом вектора), а другая — второй (концом вектора). Направление нулевого вектора, естественно, не определено.
Ненулевой вектор АВ кроме направленного отрезка определяет также содержащие его луч (с началом в точке ) и прямую (рис.1.1,а).
Коллинеарные векторы
Два ненулевых коллинеарных вектора называются одинаково направленными (сонаправленными), если они принадлежат параллельным прямым и их концы лежат в одной полуплоскости от прямой, проходящей через их начала (рис.1.2,а); либо, если векторы принадлежат одной прямой, и луч, определяемый одним вектором, целиком принадлежит лучу, определяемому другим вектором (рис. 1.2,6). В противном случае коллинеарные векторы называются противоположно направленными (рис.1.2,в,г). Одинаково направленные и противоположно направленные векторы обозначаются парами стрелок и соответственно. Понятия коллинеарных, одинаково направленных векторов распространяются на любое число векторов.
Компланарные векторы
Три ненулевых вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях (рис.1.3,а), в противном случае они называются некомпланарными (рис. 1.3,6). Так как направление нулевого вектора не определено, он считается компланарным с любыми двумя векторами. Понятие компланарных векторов распространяется на любое число векторов.
Равные векторы
Два вектора называются равными, если они:
а) коллинеарны, одинаково направлены;
б) имеют равные длины.
Все нулевые векторы считаются равными друг другу.
Это определение равенства векторов характеризует так называемые свободные векторы. Данный свободный вектор можно переносить, не меняя его направления и длины, в любую точку пространства (откладывать от любой точки), при этом будем получать векторы, равные данному. Таким образом, свободный вектор определяет целый класс равных ему векторов, отличающихся только точкой приложения. Далее будут рассматриваться, как правило, свободные векторы, при этом слово «свободные» будет опускаться.
2. Отношение равенства векторов является отношением эквивалентности. В самом деле, для отношения равенства ( — «вектор равен вектору «), определенного на множестве упорядоченных пар векторов, выполняются следующие условия:
а) каждый вектор равен самому себе (рефлексивность);
Это означает, что множество векторов разбивается на непересекающиеся классы (см. разд.В.З), т.е. с каждым вектором связывается целый класс равных ему векторов, отличающихся только точками приложения. Поэтому говорят [37], что свободный вектор определяет класс равных ему векторов.
Используя это построение, можно дать эквивалентные определения коллинеарности и компланарности. Два ненулевых вектора называются коллинеарными, если после приложения их к одной точке они лежат на одной прямой. Три ненулевых вектора называются компланарными, если после приложения их к одной точке они лежат в одной плоскости.
5. Кроме свободных векторов в приложениях векторной алгебры используются скользящие векторы, связанные (приложенные) векторы и др., которые отличаются от свободных векторов определением равенства. Например, скользящие векторы называются равными, если они лежат на одной прямой, одинаково направлены и имеют равные длины. Другими словами, в отличие от свободного вектора, скользящий вектор можно переносить, не меняя направления и длины, только вдоль содержащей этот вектор прямой. Например, в механике сила, действующая на абсолютно твердое тело, изображается скользящим вектором, а угловая скорость — свободным вектором. Сила, действующая на деформируемое тело, является примером так называемого приложенного вектора. Изменение точки приложения силы приведет к изменению ее воздействия на тело.
Пример 1.1. Дан треугольник (рис. 1.6), точки — середины его сторон. Для векторов, изображенных на рис. 1.6, указать коллинеарные, одинаково направленные, противоположно направленные, равные.
Определение вектора
В статье пойдет речь о том, что такое вектор, что он из себя представляет в геометрическом смысле, введем вытекающие понятия.
Для начала дадим определение:
Вектор – это направленный отрезок прямой.
Исходя из определения, под вектором в геометрии отрезок на плоскости или в пространстве, который имеет направление, и это направление задается началом и концом.
Нулевой вектор
Под нулевым вектором 0 → будем понимать любую точку плоскости или пространства.
Из определения становится очевидным, что нулевой вектор может иметь любое направление на плоскости и в пространстве.
Длина вектора
Под длиной вектора A B → понимается число, большее либо равное 0, и равное длине отрезка АВ.
Понятия модуль вектора и длина вектора равносильны, потому что его обозначение совпадает со знаком модуля. Поэтому длину вектора также называют его модулем. Однако грамотнее использовать термин «длина вектора». Очевидно, что длина нулевого вектора принимает значение ноль.
Коллинеарность векторов
Два вектора лежащие на одной прямой или на параллельных прямых называются коллинеарными.
Два вектора не лежащие на одной прямой или на параллельных прямых называются неколлинеарными.
Следует запомнить, что Нулевой вектор всегда коллинеарен любому другому вектору, так как он может принимать любое направление.
Коллиниарные векторы в свою очередь тоже можно разделить на два класса: сонаправленные и противоположно направленные.
Направление векторов
Считается, что нулевой вектор является сонаправленым к любым другим векторам.
Равные и противоположные векторы
Равными называются сонаправленные вектора, у которых длины равны.
Противопожными называются противоположно направленные вектора, у которых их длины равны.
Введенные выше понятия позволяют нам рассматривать векторы без привязки к конкретным точкам. Иначе говоря, можно заменить вектор равным ему вектором, отложенным от любой точки.
Углы между векторами
Угол φ = ∠ A O B называется углом между векторами a → = O A → и b → = O B → .
Очевидно, что угол между сонаправленными векторами равен нулю градусам (или нулю радиан), так как сонаправленные векторы лежат на одной или на параллельных прямых и имеют одинаковое направление, а угол между противоположно направленными векторами равен 180 градусам (или π радиан), так как противоположно направленные векторы лежат на одной или на параллельных прямых, но имеют противоположные направления.
Перпендикулярными называются два вектора, угол между которыми равен 90 градусам (или π 2 радиан).
Что такое направление вектора
Сформулируем ряд базовых определений.
Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или на параллельных плоскостях. Если среди трех векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы компланарны.
то есть модуль вектора равен корню квадратному из суммы квадратов его координат.
Обозначим углы между вектором и осями координат через α, β, γ соответственно. Косинусы этих углов называются для вектора 
направляющими, и для них выполняется соотношение: 
Верность данного равенства можно показать с помощью свойства проекции вектора на ось, которое будет рассмотрено в нижеследующем пункте 4.
Пусть в трехмерном пространстве заданы векторы 
своими координатами. Имеют место следующие операции над ними: линейные (сложение, вычитание, умножение на число и проектирование вектора на ось или другой вектор); не линейные – различные произведения векторов (скалярное, векторное, смешанное).
1. Сложение двух векторов производится покоординатно, то есть если
Геометрически два вектора складываются по двум правилам:
а) правило треугольника – результирующий вектор суммы двух векторов соединяет начало первого из них с концом второго при условии, что начало второго совпадает с концом первого вектора; для суммы векторов – результирующий вектор суммы соединяет начало первого из них с концом последнего вектора-слагаемого при условии, что начало последующего слагаемого совпадает с концом предыдущего;
б) правило параллелограмма (для двух векторов) – параллелограмм строится на векторах-слагаемых как на сторонах, приведенных к одному началу; диагональ параллелограмма исходящая из их общего начала, является суммой векторов.
Геометрически два вектора складываются по уже упомянутому правилу параллелограмма с учетом того, что разностью векторов является диагональ, соединяющая концы векторов, причем результирующий вектор направлен из конца вычитаемого в конец уменьшаемого вектора.
При λ>0 – вектор 
сонаправлен ; λ противоположно направлен ; | λ|> 1 – длина вектора увеличивается в λ раз; | λ| 1 – длина вектора уменьшается в λ раз.
4. Пусть в пространстве задана направленная прямая (ось l ), вектор 
задан координатами конца и начала. Обозначим проекции точек A и B на ось l соответственно через A ’ и B ’.
Рассмотрим некоторые основные свойства проекций:
1) проекция вектора на ось l равна произведению модуля вектора на косинус угла между вектором и осью, то есть 
;
2.) проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол – прямой;
3) проекция суммы нескольких векторов на одну и ту же ось равна сумме проекций на эту ось.
Сформулируем определения и теоремы о произведениях векторов, представляющих нелинейные операции над векторами.
5. Скалярным произведением 
векторов и 
называется число (скаляр), равное произведению длин этих векторов на косинус угла φ между ними, то есть
Теорема 2.2. Необходимым и достаточным условием перпендикулярности двух векторов является равенство нулю их скалярного произведения 
Следствие. Попарные скалярные произведения единичных орт равны нулю, то есть 
Отсюда следует условие перпендикулярности ненулевых векторов и :
С помощью скалярного произведения векторов находят работу постоянной силы 
на прямолинейном участке пути.
Решение. Вычислим модули векторов и их скалярное произведение по теореме (2.3):
Пример 2.10. Затраты сырьевых и материальных ресурсов, используемых на производство одной тонны творога, заданы в таблице 2.2 (руб.).
Какова общая цена этих ресурсов, затрачиваемых на изготовление одной тонны творога?
Примечание. Действия с векторами, осуществленные в примере 2.10, можно выполнить на персональном компьютере. Для нахождения скалярного произведения векторов в MS Excel используют функцию СУММПРОИЗВ( ), где в качестве аргументов указываются адреса диапазонов элементов матриц, сумму произведений которых необходимо найти. В MathCAD скалярное произведение двух векторов выполняется при помощи соответствующего оператора панели инструментов Matrix 
Решение. Находим вектор перемещения, вычитая из координат его конца координаты начала
Угол φ между и 
находим по формуле (2.29), то есть
– 
перпендикулярен векторам и ;
– векторы 
образуют правую тройку (рис. 2.15).
Примечание. Определитель (2.25) раскладывается по свойству 7 определителей
Следствие 1. Необходимым и достаточным условием коллинеарности двух векторов является пропорциональность их соответствующих координат
Следствие 2. Векторные произведения единичных орт равны 
Следствие 3. Векторный квадрат любого вектора равен нулю
Также с помощью векторного произведения можно определить момент силы относительно точки и линейную скорость вращения.
— перпендикулярен плоскости, проходящей через точки O , A , B ;
Следовательно, момент силы относительно точки O представляет собой векторное произведение
Решение. Найдем векторное произведение заданных векторов по формуле (2.32).
Теорема 2.6. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения
Теорема 2.7. Если три вектора 
заданы своими координатами, то их смешанное произведение представляет собой определитель третьего порядка, составленный из координат векторов- сомножителей соответственно, то есть
Объем треугольной пирамиды, построенной на этих же векторах, равен
Решение. Найдем координаты векторов
По формуле (2.36) объем пирамиды, построенной на векторах 
равен 
(единиц объема)
Рассмотрим очень важный вопрос о разложении вектора по базису. Приведем следующие определения.
получим выражение вектора 
через остальные векторы 
Линейно независимыми называют векторы, если равенство (2.37) выполняется только тогда, когда все
Базисом n – мерного пространства En называют любую совокупность линейно независимых векторов n – мерного пространства.
Произвольный вектор 
n – мерного пространства можно представить в виде линейной комбинации векторов базиса таким образом:
Линейное пространство называется конечномерным и имеет размерность n , если в этом пространстве существует система из n линейно независимых векторов (базис) такая, что каждое ее расширение приводит к линейной зависимости системы.