Что такое настоящая математика
Что мы знаем о современной математике
Как человек, который постоянно отслеживает новости науки, могу уверенно сказать — новости об открытиях и исследованиях в математике приходят редко. Возникает ощущение, что в физике или биологии что ни день, то открытие, а математика — это Перельманы раз в десятилетие. Чем занимаются современные математики, что важного происходит в этой науке и почему мы так мало о ней знаем — обо всем этом мы спросили математиков и популяризаторов этой науки.
На вопросы Научной России отвечали:
— заведующий лабораторией популяризации и пропаганды математики Математического института им. В. А. Стеклова, кандидат физико-математических наук, лауреат премии «Просветитель» 2015 года Николай Андреев.
— доктор физико-математических наук, сотрудник МФТИ, РЭШ, ЦЭМИ РАН, автор более ста научно-популярных курсов по математике Алексей Савватеев.
Сложности популяризации математики
«Сегодняшние открытия часто делаются на тех ступенях, которые нельзя объяснить простым людям. А вот то, что происходит на уровне простого языка, то и попадает в новости. Обычно это великие открытия. Если открытие сделано в задаче, которую можно сформулировать простым языком, это великое открытие», — говорит Алексей Савватеев.
Несмотря на то, что все мы в школе, хотели мы того или нет, занимались математикой очень много, мы не изучили и сотой доли всех тех понятий и даже общих закономерностей, что существует в этой науке. А значит, уже начав разбираться с каким-то исследованием, мы натолкнемся на то, что не понимаем даже слов, что употребляет ученый.
«Для объяснения любого открытия придется ввести очень много контекста, а в некоторых областях много определений уже на начальном этапе, чтобы в итоге дойти до сути. В общем, входной билет очень дорогой», — говорит Николай Андреев.
Сложно, но не невозможно. Пример тому — и блестящие книги по математике для широкого круга читателей, одну из которых — «Математическая составляющая» — жюри «Просветителя» признало лучшей в 2015 году. В книге, над которой работал большой авторский коллектив, действительно, достаточно понятным языком рассказывается о работе математиков. Появляются и курсы по математике для всех желающих, где основы этой науки лекторы стараются донести даже до самых ярко выраженных гуманитариев, причем они оказываются неожиданно популярны — так, на онлайн-курс Алексея Савватеева к его собственному удивлению записалось несколько тысяч человек.
Одна из главных сложностей с популяризацией математики связана с тем, что исследования в этой науке очень редко удается ярко визуализировать. «Если вы придете в любой музей науки, вы увидите, что там физических, химических, биологических экспонатов много, а математических — почти нет», — говорит Николай Андреев. Тем не менее, эту задачу уже давно и вполне успешно решает проект Андреева «Математические этюды».
Еще одна сложность, о которой говорят многие математики, занимающиеся популяризацией — страх перед этой наукой, укоренившийся у многих еще со школы. Отчасти он связан с проблемами преподавания математики в школе, а отчасти со вполне объективной сложностью этой науки.
«Математика постоянно на всех уровнях требует очень высокого понимания. Если ты не понял, как дроби складывать, то и дальше сложно будет», — говорит Николай Андреев.
«Это ступень за ступенью постижение. И каждая ступень — это огромные усилия над собой, каждый отпадает на своей ступени. Это, действительно, вызов для интеллекта, ведь математика — это, можно сказать, концентрированная сложность мира. А мир — он так устроен, он сложный, потому и математика сложная», — добавляет Алексей Савватеев.
Революция, которую никто не замечает
«За последние несколько десятилетий математиками доказано, как минимум, три величайшие гипотезы, сняты проблемы, стоявшие столетиями. Я считаю, что в математике происходит самая настоящая революция, только ее никто не замечает», — говорит Алексей Савватеев.
Итак, великие открытия, которые мы не заметили — это Проблема четырех красок, Великая теорема Ферма, Гипотеза Пуанкаре и проблема узлов. Памятуя о сложностях перевода с математического языка на русский обывательский, попробуем хотя бы кратко рассказать о том, что это за открытия.
Теорема о четырех красках была сформулирована в 1852 году и доказана только в 1976 году, став, кстати, первой значимой теоремой, доказанной при помощи компьютера. Согласно этой теореме, всякую расположенную на сфере карту можно раскрасить четырьмя красками так, чтобы любые две области, имеющие общий участок границы, были раскрашены в разные цвета.
Вот зачем нужна школьная алгебра
Обычно на вопрос «зачем нужна математика?» отвечают что-то вроде «гимнастика для ума». На мой взгляд, этого объяснения недостаточно. Когда человек выполняет физические упражнения, то он знает точное название групп мышц, которые при этом развиваются. Но разговоры про математику остаются слишком абстрактными. Какие конкретно «мышцы ума» тренируются школьной алгеброй? Она ведь совсем не похожа на настоящую математику, в которой делаются великие открытия. Что дает умение искать производную каких-то запутанных функций?
Преподавание программирования слабым студентам привело меня к более точному ответу на вопрос «зачем?». В статье я постараюсь донести его вам.
В данном примере от ученика ожидают, что он вспомнит формулу квадрата суммы
В более сложных случаях, полученное выражение можно использовать для других преобразований. Например:
преобразуется сначала в
Чтобы добиться такого результата, ученику нужно распознать в исходном выражении и потом применить три формулы:
Это практически определение рефакторинга из одноименной книги Мартина Фаулера.
В своем труде, автор формулирует их следующим образом:
Рефакторинг (Refactoring) (сущ.): изменение во внутренней структуре программного обеспечения, имеющее целью облегчить понимание его работы и упростить модификацию, не затрагивая наблюдаемого поведения.
Производить рефакторинг (Refactor) (глаг.): изменять структуру программного обеспечения, применяя ряд рефакторингов, не затрагивая его поведения.
В книге даются «формулы», которые нужно распознать в исходном коде и правила их преобразования.
В качестве простейшего примера, приведу «введение поясняющей переменной» из книги:
Части выражения нужно записать в переменную, имя которой поясняет его назначение.
Представьте себе человека, который не может упрощать алгебраические выражения с использованием формулы квадрата суммы и разности квадратов.
Как вы думаете, сможет ли этот человек рефакторить код?
Сможет ли он вообще написать понятный другим людям код, если у него не сформирован идеал этой самой лаконичности? На мой взгляд — нет.
Однако в школе учатся все, а программистами становится меньшинство. Полезен ли навык преобразования выражений для обычных людей? Я думаю да. Только навык применяется в более абстрактном виде: нужно оценить ситуацию и выбрать дальнейшее действие так, чтобы приблизиться к цели. В педагогике этот феномен называется перенос (навыка).
Даже при езде на автомобильном транспорте, водитель постоянно занимается распознаванием шаблонов в окружающем мире и выполнением соответствующих маневров, чтобы добраться до цели.
Когда ты умер, ты об этом не знаешь, только другим тяжело. То же самое, когда ты не освоил математику…
Что же происходит, если человеку не удалось освоить преобразование выражений? Время от времени я веду индивидуальные занятия со студентами, у которых в школе было плохо с математикой. Как правило, они напрочь застревают на теме про циклы. Настолько, что с ними приходится заниматься «алгеброй», но на языке программирования.
Это происходит потому, что при написании циклов основной прием как раз и заключается в том, чтобы преобразовать группу одинаковых выражений.
Допустим результат работы программы должен выглядеть так:
Введение
Глава 1
Глава 2
Глава 3
Глава 4
Глава 5
Глава 6
Глава 7
Заключение
Тривиальная программа для достижения этого результата выглядит так:
Но это решение далеко от лаконичного идеала. Сначала в нем нужно найти повторяющуюся группу действий и потом преобразовать. В итоге получится такое решение:
Если же человек в свое время не освоил математику, то и выполнять подобные преобразования он не сможет. У него просто не будет соответствующего навыка. Именно поэтому тема циклов — первое препятствие в обучении разработчика.
Похожие проблемы возникают и в других областях. Если человек не умеет использовать подручный инструмент, то он не сможет проявлять бытовую смекалку. Злые языки будут говорить, что руки не из того места растут. На дороге это проявляется в неумении правильно оценить ситуацию и выбрать маневр. Что иногда может привести к трагическим последствиям.
Зачем нужна математика
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Интересные факты про математику
Математика — это не только арифметические задачки. Это особый язык, который учит думать и рассуждать.
Математику называют междисциплинарной наукой, потому что она тесно связана с физикой, географией, геологией, химией. Социология и экономика неотделимы от математики, поэтому многие выводы из гуманитарных исследований опираются на математические понятия и логические законы.
Мир изменился и стал более технологичным, поэтому для любителей математики открыто множество вариантов профессионального развития.
Если 15 лет назад перспективными были сферы маркетинга и юриспруденции, то сегодня лидирует IT.
Профессиональная востребованность = понимание технологий + способность к решению нестандартных задач. И ключ к успеху — знание математики.
Что отличает математику от других школьных предметов:
Математика развивает мышление
Зачем заниматься физкультурой? Ответ простой — для здоровья и красоты тела.
Зачем учить математику? Ответ на этот вопрос кажется менее очевидным.
Математика — это гимнастика для ума. Хочешь не хочешь, но в процессе изучения будут крепчать качества, которые влияют на способ мышления. Для этого не обязательно учиться в профильном классе и участвовать в олимпиадах — решение даже самых простых задачек на пропорции или с процентами дает значительный эффект.
Обобщение, сокращение, анализ, систематизация, выделение важного, поиск закономерностей, формулирование гипотез и доказательство теорий — все это помогает развить мышление, сделать его более гибким. Точно также, как физические упражнения делают наше тело подвижнее, дают заряд сил и тренируют выносливость, математика тренирует ум.
Математика развивает интеллект. Набор правил и функций, которые мы изучаем в школе, делают наше мышление последовательным и логичным. Это отражается на умении рассуждать, формулировать мысли и замечать взаимосвязи. И самое увлекательное, что эти знания можно (и нужно!) применять не только в школе, но и в нестандартных ситуациях: чтобы выбрать самую выгодную банковскую карту, просчитать литры краски для ремонта или создать карту сокровищ, чтобы не забыть где они спрятаны.
Математика — универсальный международный язык, которым владеют почти все люди на земле. Эти знания пригодятся в любой стране и могут стать предметом интересной беседы.
Что понять, зачем учить математику в школе, только представьте, как приятно, когда в голове нет «каши» и путаницы в рассуждениях. На этот счет еще в прошлом веке великий учёный Ломоносов сказал: «Математику только затем учить надо, что она ум в порядок приводит». Как тут можно спорить? 😇
Математика формирует характер
Чтобы правильно решать математические задачи, недостаточно одних лишь знаний. Нужны такие качества характера, как внимательность, настойчивость, последовательность, точность и аккуратность. Чем регулярнее мы практикуемся, тем сильнее укрепляются эти черты. И еще бонус: эти качества можно применять не только на уроках в школе, но и в других сферах жизни.
Чем сложнее математические задачи, тем больше усилий и навыков нужно приложить для их решения.
Благодаря математике можно избавиться от вредных привычек:
Домысливать и не уметь объяснять, почему думаешь именно так
Оперировать фактами и точными терминами и быть более убедительным
Запоминать информацию механически, «зазубривать»
Оценивать, анализировать, строить аналогии и подвергать критике
Математика тренирует память
Ученые из Стэнфордского университета в США изучили, как человек решает математические задачи и выяснили, что взрослые люди используют для этого навык «доставать» из памяти ответы на основе прошлого опыта.
Почему учителя настаивают на регулярном посещении уроков? Дело не в их вредности, а в том, что при решении математических задач, мы «достаем» из памяти ответы на основе прошлого опыта. А чтобы этот опыт закрепить, нужно повторять материал и тренироваться в решении примеров. Только так можно запомнить все правила и формулы. 🤓
В журнале Nature Neuroscience в 2014 году опубликовали исследование про роль определенных областей головного мозга в развитии познавательной активности детей. Оказалось, что на интерес к знаниям оказывает сильное влияние гиппокамп — часть мозга, которая отвечает за память.
Интересный факт! Определенные области головного мозга влияют на развитие познавательной активности детей. Например, на интерес к знаниям влияет часть мозга, которая отвечает за память — гиппокамп. Поэтому:
Математика — волшебница, не иначе! Систематизируем все волшебные свойства и повторим, какие навыки можно развить с помощью математики:
Математика
Содержание
Основные сведения
Идеализированные свойства исследуемых объектов либо формулируются в виде аксиом, либо перечисляются в определении соответствующих математических объектов. Затем по строгим правилам логического вывода из этих свойств выводятся другие истинные свойства (теоремы). Эта теория в совокупности образует математическую модель исследуемого объекта. Таким образом первоначально, исходя из пространственных и количественных соотношений, математика получает более абстрактные соотношения, изучение которых также является предметом современной математики.
Традиционно математика делится на теоретическую, выполняющую углублённый анализ внутриматематических структур, и прикладную, предоставляющую свои модели другим наукам и инженерным дисциплинам, причём некоторые из них занимают пограничное с математикой положение. В частности, формальная логика может рассматриваться и как часть философских наук, и как часть математических наук; механика — и физика, и математика; информатика, компьютерные технологии и алгоритмика относятся как к инженерии, так и к математическим наукам и т. д. В литературе было предложено много различных определений математики (см. ниже).
Этимология
В текстах на русском языке слово «математика» или «мафематика» встречается по крайней мере с XVII века, например, у Николая Спафария в «Книге избранной вкратце о девяти мусах и о седмих свободных художествах» (1672 год) [5]
Определения
Одно из первых определений предмета математики дал Декарт [6] :
К области математики относятся только те науки, в которых рассматривается либо порядок, либо мера и совершенно не существенно, будут ли это числа, фигуры, звёзды, звуки или что-нибудь другое, в чём отыскивается эта мера. Таким образом, должна существовать некая общая наука, объясняющая всё относящееся к порядку и мере, не входя в исследование никаких частных предметов, и эта наука должна называться не иностранным, но старым, уже вошедшим в употребление именем Всеобщей математики.
Математика… наука о количественных отношениях и пространственных формах действительного мира.
Это определение Энгельса [8] ; правда, далее Колмогоров поясняет, что все использованные термины надо понимать в самом расширенном и абстрактном смысле.
Сущность математики… представляется теперь как учение об отношениях между объектами, о которых ничего не известно, кроме описывающих их некоторых свойств,— именно тех, которые в качестве аксиом положены в основание теории… Математика есть набор абстрактных форм — математических структур.
Приведём ещё несколько современных определений.
Герман Вейль пессимистически оценил возможность дать общепринятое определение предмета математики:
Вопрос об основаниях математики и о том, что представляет собой в конечном счёте математика, остаётся открытым. Мы не знаем какого-то направления, которое позволит в конце концов найти окончательный ответ на этот вопрос, и можно ли вообще ожидать, что подобный «окончательный» ответ будет когда-нибудь получен и признан всеми математиками.
Разделы математики
1. Математика как учебная дисциплина подразделяется в Российской Федерации на элементарную математику, изучаемую в средней школе и образованную дисциплинами:
и высшую математику, изучаемую на нематематических специальностях вузов. Дисциплины, входящие в состав высшей математики, варьируются в зависимости от специальности.
Программа обучения по специальности математика [13] образована следующими учебными дисциплинами:
2. Математика как специальность научных работников Министерством образования и науки Российской Федерации [14] подразделяется на специальности:
3. Для систематизации научных работ используется раздел «Математика» [15] универсальной десятичной классификации (УДК).
4. Американское математическое общество (AMS) выработало свой стандарт для классификации разделов математики. Он называется Mathematics Subject Classification. Этот стандарт периодически обновляется. Текущая версия — это MSC 2010. Предыдущая версия — MSC 2000.
Обозначения
Вследствие того, что математика работает с чрезвычайно разнообразными и довольно сложными структурами, система обозначений также очень сложна. Современная система записи формул сформировалась на основе европейской алгебраической традиции, а также математического анализа (понятия функции, производной и т. д.). Геометрия испокон века пользовалась наглядным (геометрическим же) представлением. В современной математике распространены также сложные графические системы записи (например, коммутативные диаграммы), нередко также применяются обозначения на основе графов.
Краткая история
Академиком А. Н. Колмогоровым предложена такая структура истории математики:
Развитие математики началось вместе с тем, как человек стал использовать абстракции сколько-нибудь высокого уровня. Простая абстракция — числа; осмысление того, что два яблока и два апельсина, несмотря на все их различия, имеют что-то общее, а именно занимают обе руки одного человека, — качественное достижение мышления человека. Кроме того, что древние люди узнали, как считать конкретные объекты, они также поняли, как вычислять и абстрактные количества, такие, как время: дни, сезоны, года. Из элементарного счёта естественным образом начала развиваться арифметика: сложение, вычитание, умножение и деление чисел.
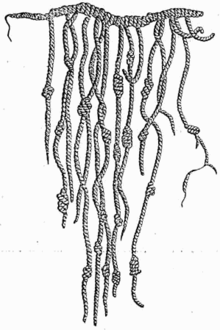
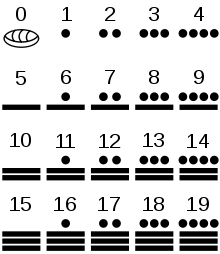
Развитие математики опирается на письменность и умение записывать числа. Наверно, древние люди сначала выражали количество путём рисования чёрточек на земле или выцарапывали их на древесине. Древние инки, не имея иной системы письменности, представляли и сохраняли числовые данные, используя сложную систему верёвочных узлов, так называемые кипу. Существовало множество различных систем счисления. Первые известные записи чисел были найдены в папирусе Ахмеса, созданном египтянами Среднего царства. Индская цивилизация разработала современную десятичную систему счисления, включающую концепцию нуля.
Исторически основные математические дисциплины появились под воздействием необходимости вести расчёты в коммерческой сфере, при измерении земель и для предсказания астрономических явлений и, позже, для решения новых физических задач. Каждая из этих сфер играет большую роль в широком развитии математики, заключающемся в изучении структур, пространств и изменений.
Философия математики
Цели и методы
Математика изучает воображаемые, идеальные объекты и соотношения между ними, используя формальный язык. В общем случае математические понятия и теоремы не обязательно имеют соответствие чему-либо в физическом мире. Главная задача прикладного раздела математики — создать математическую модель, достаточно адекватную исследуемому реальному объекту. Задача математика-теоретика — обеспечить достаточный набор удобных средств для достижения этой цели.
Содержание математики можно определить как систему математических моделей и инструментов для их создания. Модель объекта учитывает не все его черты, а только самые необходимые для целей изучения (идеализированные). Например, изучая физические свойства апельсина, мы можем абстрагироваться от его цвета и вкуса и представить его (пусть не идеально точно) шаром. Если же нам надо понять, сколько апельсинов получится, если мы сложим вместе два и три, — то можно абстрагироваться и от формы, оставив у модели только одну характеристику — количество. Абстракция и установление связей между объектами в самом общем виде — одно из главных направлений математического творчества.
Другое направление, наряду с абстрагированием — обобщение. Например, обобщая понятие «пространство» до пространства n-измерений. «Пространство 

Изучение внутриматематических объектов, как правило, происходит при помощи аксиоматического метода: сначала для исследуемых объектов формулируются список основных понятий и аксиом, а затем из аксиом с помощью правил вывода получают содержательные теоремы, в совокупности образующие математическую модель.
Основания
Вопрос сущности и оснований математики обсуждался со времён Платона. Начиная с XX века наблюдается сравнительное согласие в вопросе, что надлежит считать строгим математическим доказательством, однако отсутствует согласие в понимании того, что в математике считать изначально истинным. Отсюда вытекают разногласия как в вопросах аксиоматики и взаимосвязи отраслей математики, так и в выборе логических систем, которыми следует при доказательствах пользоваться.
Помимо скептического, известны нижеперечисленные подходы к данному вопросу.
Теоретико-множественный подход
Предлагается рассматривать все математические объекты в рамках теории множеств, чаще всего с аксиоматикой Цермело — Френкеля (хотя существует множество других, равносильных ей). Данный подход считается с середины XX века преобладающим, однако в действительности большинство математических работ не ставят задач перевести свои утверждения строго на язык теории множеств, а оперируют понятиями и фактами, установленными в некоторых областях математики. Таким образом, если в теории множеств будет обнаружено противоречие, это не повлечёт за собой обесценивание большинства результатов.
Логицизм
Данный подход предполагает строгую типизацию математических объектов. Многие парадоксы, избегаемые в теории множеств лишь путём специальных уловок, оказываются невозможными в принципе.
Формализм
Данный подход предполагает изучение формальных систем на основе классической логики.
Интуиционизм
Интуиционизм предполагает в основании математики интуиционистскую логику, более ограниченную в средствах доказательства (но, как считается, и более надёжную). Интуиционизм отвергает доказательство от противного, многие неконструктивные доказательства становятся невозможными, а многие проблемы теории множеств — бессмысленными (неформализуемыми).
Конструктивная математика
Основные темы
Числа
Понятие «число» первоначально относилось к натуральным числам. В дальнейшем оно было постепенно распространено на целые, рациональные, действительные, комплексные и другие числа.
| |||||||||||||||
 |  | ||||||||||||||
| Комплексные числа | Кватернионы | ||||||||||||||
 Числовые системы Числовые системы | |
|---|---|
| Счётные множества | Натуральные числа ( ) • Целые ( ) • Целые ( ) • Рациональные ( ) • Рациональные ( ) • Алгебраические ( ) • Алгебраические ( ) • Периоды • Вычислимые • Арифметические ) • Периоды • Вычислимые • Арифметические |
| Вещественные числа и их расширения | Вещественные ( ) • Комплексные ( ) • Комплексные ( ) • Кватернионы ( ) • Кватернионы ( ) • Числа Кэли (октавы, октонионы) ( ) • Числа Кэли (октавы, октонионы) ( ) • Седенионы ( ) • Седенионы ( ) • Альтернионы • Процедура Кэли — Диксона • Дуальные • Гиперкомплексные • Суперреальные • Гиперреальные • Surreal number (англ.) ) • Альтернионы • Процедура Кэли — Диксона • Дуальные • Гиперкомплексные • Суперреальные • Гиперреальные • Surreal number (англ.) |
| Другие числовые системы | Кардинальные числа • Порядковые числа (трансфинитные, ординал) • p-адические • Супернатуральные числа |
| См. также | Двойные числа • Иррациональные числа • Трансцендентные • Числовой луч • Бикватернион |
Преобразования
 | 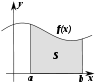 |  |  |
| Арифметика | Дифференциальное и интегральное исчисление | Векторный анализ | Анализ |
 |  |  | |
| Дифференциальные уравнения | Динамические системы | Теория хаоса |
Структуры
Пространственные отношения
Более наглядные подходы в математике.
Дискретная математика
Дискретная математика включает средства, которые применяются над объектами, способными принимать только отдельные, не непрерывные значения.
 | 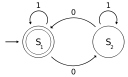 |  |  |
| Математическая логика | Теория вычислимости | Криптография | Теория графов |
Коды в системах классификации знаний
Онлайновые сервисы
Существует большое число сайтов, предоставляющих сервис для математических расчётов. Большинство из них англоязычные. [20] Из русскоязычных можно отметить сервис математических запросов поисковой системы Nigma.