Что такое натуральное число метров

Измерение величин и именованные числа

С начала 5 класса мы с вами изучали только натуральные числа. Они исторически появились первыми как результат удовлетворения потребности человека в более удобном и качественном счете предметов. Но уже в те далекие времена люди поняли, что не все можно посчитать только такими числами, которые мы сегодня называем натуральные.

Поэтому, таким же естественным путем, каким были введены в жизнь человека натуральные числа, произошло появление дробных и смешанных чисел, речь о которых пойдет в следующих уроках. Этот же урок рассматривает одно из важнейших человеческих действий, которое напрямую привело к необходимости введения нового огромного класса чисел.

Измерение величин

Давайте представим, что нам нужно определить точное расстояние, к примеру, от одного конца комнаты до другого, то есть, узнать длину комнаты. Мы, конечно, можем при достаточных усилиях сделать это так, как в мультфильме «38 попугаев» – посчитать ее в мартышках, попугаях или слонятах. Но если мы так поступим, то мы не сможем сделать так, чтобы нас поняли другие, потому что размеры этих животных могут быть разные, и у каждого могут быть свои представления о них. Не водить же зверей все время с собой?

Единица измерения какой-либо величины – это известная всем величина, которая принята в качестве основной меры для измерения других величин этого же рода.

Измерить величину – это означает определить, какое количество единиц измерения содержится в этой величине.

Можно выразить это определение более обобщенно.

Измерить величину – это означает определить, какое количество известных величин этого же рода, принятых в качестве единицы измерения, содержится в этой величине.

Меры измерений величин

Однородные меры – это такие меры, которые применяются для измерения однородных величин.

Отношение однородных мер – это показатель, который равен количеству меньших мер, содержащихся в большей мере. Иными словами, сколько раз можно в большей мере поместить меньшую.

Например, отношение сантиметра к миллиметру – это число 10.

Метрическая система мер

Меры длины

Соотношения величин вы можете всегда посмотреть в справочнике.

Кроме этого, метр также собирается в более крупные меры, по 10 более мелких частей в каждой. 10 метров – это декаметр (произошло от древнегреческого δέκα – десять), 100 метров – гектометр (древнегреческого ἑκατόν – сто), 1000 метров – километр (от древнегреческого χῑλιάς – тысяча).

Меры площади

Так, один квадратный метр – это площадь квадрата, у которого сторона равна 1 метру, один квадратный километр – это площадь квадрата с длиной стороны 1 километр.

Одна квадратная мера площади состоит из 100 мер более низкого соседнего с ней разряда.

Для обозначения площадей полей и лесов применяют два особых названия.

Меры объема

Одна кубическая мера объема состоит из 1000 мер более низкого соседнего с ней разряда.

Меры веса

Конечно, с точки зрения физики правильно говорить масса, а не вес. Но мы используем эти слова в повседневном обиходе как синонимы, поэтому и я допускаю подобную трактовку в своих уроках математики.

Кроме этих мер свои названия имеют и более крупные группировки: в 1 центнере находится 100 килограмм, а в 1 тонне – 1000 килограмм.

Меры объема жидкостей

Литр – это объем, который заполняет один килограмм воды при определенных условиях: нормальное атмосферное давление и максимальная плотность воды.

10 литров составляют 1 декалитр, 100 литров образуют гектолитр, 1000 литров – 1 килолитр.

Единицы измерения времени

Существуют две основные меры времени.

Сутки – это величина времени, приближенно равная одному обороту нашей планеты Земля вокруг своей оси.

Год – это такая величина времени, которая приближенно равна одному полному обороту Земли вокруг Солнца.

Часы в сутках считают сразу от 1 до 24, или разбивают на две части по 12 часов и считают от 1 до 12 (до полудня), а затем опять от 1 до 12 (уже до полуночи). При этом для уточнения периода суток добавляют: «до полудня», «после полудня» или указывают: «ночи», «утра», «дня» или «вечера».

Так, 15 часов – это 3 часа после полудня, или просто 3 часа дня, а 22 часа – это 10 часов после полудня, или 10 часов вечера.

Про год и летоисчисление вы узнаете больше из этой статьи.

Именованные числа

Именованное число – это числовое выражение величины измерения совместно с указанием единиц измерения этой величины.

Отвлеченное число – это просто число без указания единицы измерения какой-либо величины.

Например, 12 деревьев, 3 килограмма, 135 литров – это именованные числа, а 12, 3 и 135 – отвлеченные.

Именованное число может состоять только из одной меры : 18 л, 312 км, 48 г, или из нескольких, но обязательно однородных: 5 кг 640 г, 12 м 72 см.

Нельзя в одном именованном числе смешивать меры разных величин, например, так: 12 кг 58 см или 15 л 12 г.

Простое именованное число – имеет в своем составе только одно наименование какой-либо величины.

Составное именованное число выражается несколькими единицами измерения одной и той же величины.

Именованные числа можно преобразовывать в более крупные или мелкие наименования однородных мер, то есть, увеличивать или уменьшать их разряд.

Превращением или укрупнением именованного числа называется его преобразование в более крупное наименование однородной меры.

Раздроблением именованного числа называется его преобразование в более мелкие единицы однородной меры.

Так, записав именованное число 5203 метра как 5 км 203 м, мы совершили превращение, а преобразовав 5 км 203 м в 5203 м, – раздробление.

Источник

Что такое натуральное число в математике?

Все дети с ранних лет изучают математику. Поначалу она позволяет узнать простые вещи, легко применимые в жизни, но с течением времени задачи постоянно усложняются. Появляется и новая терминология, по которой не всегда можно понять, что имеется в виду. Например, что такое натуральное число в математике?

В древние времена люди не пользовались цифрами так, как делают это сейчас, однако счет всё равно был им необходим. Предметы сравнивались по количеству с чем-то, например, кто-то имел столько же ягод, сколько и пальцев на одной руке. Постепенно люди изобрели систему счета, а с ней появились и новые термины.

Что такое натуральное число в математике?

Это понятие относится к одним из самых старых, так как оно родилось из-за древней необходимости научиться считать количество обычных предметов. Что значит натуральное число? Чаще всего дается следующее определение – это числа, которые возникают при подсчете, причем происходит подобное естественным образом.

Отсюда берется и второе название этого термина – естественные числа. Своей последовательностью, расположенностью по возрастанию, они образуют натуральный ряд. Иначе говоря, все цифры, начиная с единицы, которые используются для подсчета предметов, являются натуральными.

Таким образом, существует самое малое натуральное число – им является единица. Наибольшего же не бывает, так как к любой цифре можно добавить ещё один. Ноль не входит в натуральный ряд, так как с его помощью нельзя ничего посчитать, хотя далеко не все ученые с этим согласны.

Определение натуральных чисел

Подобные цифры определяются двумя главными методами. Первый из них подразумевает перечисление всего имеющегося, а второй называет итоговое количество.

В этой цифре и заключается основная разница между двумя данными методами определения. В первом случае минимальным числом является единица, а во втором возможно и использование нуля. Математики так и не смогли прийти к единогласному решению о том, какой метод лучше, и стоит ли ставить ноль в один ряд с другими натуральными числами.

Как правило, применяется всё же первый вариант, оставляющий спорную цифру в стороне. Тем не менее, в некоторых трудах, вроде Бурбаки, используется другой подход. Помимо этого, ноль является неотъемлемой и широко применяемой частью в мире программирования.

Особенности натуральных чисел

Главное, о чем нужно помнить при упоминании подобных чисел, так это об их обязанности быть естественными. Они должны быть такими, чтобы с их помощью было возможно подсчитать количество каких-то предметов. Естественные числа должны быть доступными и понятными для всех.

По этой причине к ним не относятся отрицательные показатели и различные нецелые числа. Например, рациональное, обозначающееся в виде дроби, или вещественные, представляющее собой математический объект, не смогут стать частью натурального ряда.

Что такое натуральное число в математике? Все эти цифры принято обозначать буквой N. Её выбрали потому, что на латинском языке слово естественный пишется как naturalis, то есть начинается с литеры N. Число, подразумеваемое под этим обозначением, бесконечно.

Нередко для доказательства сложных теорем полезно помнить и о нуле. Он входит в расширенный натуральный ряд, который обозначают с помощью соответствующей цифры, приписанной снизу к букве N. Иногда вместо неё применяете Z, вновь с тем же маленьким нулем рядом.

Операции с натуральными числами

В математике существует понятие замыкания. Оно обозначает минимально возможное расширение какого-то множества, операции с которым не выходят за его пределы. В отношении натуральных чисел выделяется несколько таких замкнутых операций.

Иногда в данном вопросе рассматриваются ещё две операции. Их проблема заключается в том, что они применимы не для всех случаев. Иногда подобное может существовать, а иногда нет. К этим операциям относятся:

Как правило, наука сосредотачивается на первых двух операциях – сложении и вычитании. Интересно, что именно они способствуют созданию кольца целых чисел – это происходит через бинарные сложения и умножения.

Что стоит знать о натуральных числах?

Цифры, используемые для счета, не всегда были такими, как мы их знаем сегодня. Изначально применялось относительно схематическое изображение, постепенно сформировавшееся в римские цифры.

Современный же вариант зародился в Индии, примерно полторы тысячи лет назад. Впоследствии они были привезены в европейские страны арабами, за что и получили своё известное название – арабские цифры. Несмотря на то, что натуральных чисел может быть любое количество, цифр всего десять – от нуля и до девятки.

Если рассматривать натуральный ряд, то в нем каждое число будет отличаться от предыдущего или последующего на единицу, при том, что сам ряд бесконечен. Однако, в процессе счета появляется так называемая десятичная позиционная.

Под этим словом подразумевается тот факт, что когда числа доходят до десяти, они образуют новую единицу старшего разряда. Эти разряды бывают самыми разными – в частности, к ним относятся миллионы и миллиарды. В зависимости от их количества, разряды объединяют по классам.

Например, миллиарды могут исчисляться десятками или сотнями. Это будут разряды, но все они в целом образуют класс миллиардов. То же самое происходит и с разрядами миллионов, тысяч, сотен, десяток и единиц.

Источник

Определите, верно ли, что значение площади (м²) кратно : 5 ; 2 ; 10 ; 8 ; 100 ; 4.

Верно для 5 ; 2 ; 10 ; 8 ; 4?

Потому что это делители 120

Если один из множителей делится, то делится и все произведение.

Длина прямоугольника — 45 м, ширина — нечётное число метров?

Длина прямоугольника — 45 м, ширина — нечётное число метров.

Можно ли сказать, что значение площади прямоугольника (в квадратных метрах) кратно 5.

Определите, верно ли, что значение площади (квадратные метры) кратно 5, 2, 10, 8, 100, 4.

Верно ли, что значение площади (кратно 2, 5, 4, 8.

A) ширина прямоугольника 6 м а длина 3 м больше ширины определи периметр и площадь этого прямоугольника б) найди другие прямоугольники с таким же периметром и определи их площадь (длины сторон прямоуг?

A) ширина прямоугольника 6 м а длина 3 м больше ширины определи периметр и площадь этого прямоугольника б) найди другие прямоугольники с таким же периметром и определи их площадь (длины сторон прямоугольника выражен целым числом метров).

Площадь прямоугольника b метров в квадрате а длина c метров на сколько метров ширина прямоугольника меньше его длины?

Площадь прямоугольника b метров в квадрате а длина c метров на сколько метров ширина прямоугольника меньше его длины.

Длина прямоугольника равна 18, 8 метров а его ширина составляет 0, 75 Определите площадь прямоугольника?

Длина прямоугольника равна 18, 8 метров а его ширина составляет 0, 75 Определите площадь прямоугольника.

Длина прямоугольника 12 метров ширина прямоугольника не известна площадь прямоугольника 72 квадратных метра?

Длина прямоугольника 12 метров ширина прямоугольника не известна площадь прямоугольника 72 квадратных метра.

Сколько прямоугольников со значением длин сторон равных натуральным числам и площадью 72см2?

Сколько прямоугольников со значением длин сторон равных натуральным числам и площадью 72см2.

Длина прямоугольника в 2 раза больше ширины?

Длина прямоугольника в 2 раза больше ширины.

Сумма длины и 3 кратной ширины прямоугольника равна 20, 5.

Вычислите площадь этого прямоугольника.

Верно ли, что любое натуральное число кратно самому себе?

Источник

Натуральное число

Натуральные числа (естественные числа) — числа, возникающие естественным образом при счёте (как в смысле перечисления, так и в смысле исчисления).

Существуют два подхода к определению натуральных чисел — числа, используемые при:

Отрицательные и нецелые (рациональные, вещественные, …) числа натуральными не являются.

Множество всех натуральных чисел принято обозначать знаком . Множество натуральных чисел является бесконечным, так как для любого натурального числа найдётся большее его натуральное число.

Содержание

Определение

Аксиомы Пеано

Множество будем называть множеством натуральных чисел, если зафиксирован некоторый элемент (единица) и функция (функция следования) так, что выполнены следующие условия

Перечисленные аксиомы отражают наше интуитивное представление о «натуральном ряде».

Поэтому, достаточно зафиксировать в качестве какую-либо одну конкретную модель множества натуральных чисел, например, ту, что описана ниже.

Теоретико-множественное определение (Определение Фреге-Рассела)

Согласно теории множеств, единственным объектом конструирования любых математических систем является множество.

Таким образом, и натуральные числа вводятся, исходя из понятия множества, по двум правилам:

Числа, заданные таким образом, называются ординальными.

Первые несколько ординальных чисел и соответствующие им натуральные числа:

Ноль как натуральное число

Иногда, в иностранной и переводной литературе, в первой и третьей аксиомах Пеано заменяют на . В этом случае ноль считается натуральным числом. При определении через классы равномощных множеств 0 является натуральным числом по определению. Специально отбрасывать его было бы неестественно. Кроме того, это значительно усложнило бы дальнейшее построение и применение теории, так как в большинстве конструкций ноль, как и пустое множество, не является чем-то выделенным. Одним из преимуществ натурального нуля является то, что при этом образует полугруппу с единицей.

В русской литературе обычно ноль исключён из числа натуральных чисел , а множество натуральных чисел с нулём обозначается как . Если в определение натуральных чисел включен ноль, то множество натуральных чисел записывается как , а без нуля как .

В международной математической литературе, с учётом сказанного выше и во избежание неоднозначностей, множество обычно называют множеством положительных целых чисел и обозначают . Множество зачастую называют множеством неотрицательных целых чисел и обозначают .

Операции над натуральными числами

К замкнутым операциям (операциям, не выводящим результат из множества натуральных чисел) над натуральными числами относятся следующие арифметические операции:

Дополнительно рассматривают ещё две операции. С формальной точки зрения они не являются операциями над натуральными числами, так как не определены для всех пар чисел (иногда существуют, иногда нет).

Следует заметить, что именно операции сложения и умножения являются основополагающими. В частности, кольцо целых чисел определяется именно через бинарные операции сложения и умножения.

Теоретико-множественные определения

Воспользуемся определением натуральных чисел как классов эквивалентности конечных множеств. Будем обозначать класс эквивалентности множества A относительно биекций как [A]. Тогда основные арифметические операции определяются следующим образом:

где — дизъюнктное объединение множеств, — прямое произведение, — множество отображений из B в A. Можно показать, что полученные операции на классах введены корректно, то есть не зависят от выбора элементов классов, и совпадают с индуктивными определениями.

Основные свойства

Алгебраическая структура

Сложение превращает множество натуральных чисел в полугруппу с единицей, роль единицы выполняет 0. Умножение также превращает множество натуральных чисел в полугруппу с единицей, при этом единичным элементом является 1. С помощью замыкания относительно операций сложения-вычитания и умножения-деления получаются группы целых чисел и рациональных положительных чисел соответственно.

Источник

Изучение точного предмета: натуральные числа это какие числа, примеры и свойства

В математике существует несколько различных множеств чисел: действительные, комплексные, целые, рациональные, иррациональные, дробные… В нашей повседневной жизни мы чаще всего используем натуральные числа, так как мы сталкиваемся с ними при счете и при поиске, обозначении количества предметов….

Какие числа называются натуральными

Из десяти цифр можно записать абсолютно любую существующую сумму классов и разрядов. Натуральными значениями считаются те, которые используются:

N значения всегда целые и положительные. Наибольшего N не существует, так как множество целых значений не ограничено.

Внимание! Натуральные числа получаются при счете предметов или при обозначении их количества.

Абсолютно любое число может быть разложено и представлено в виде разрядных слагаемых, например: 8.346.809=8 миллионов+346 тысяч+809 единиц.

Множество N

Множество N находится в множестве действительных, целых и положительных. На схеме множеств они бы находились друг в друге, так как множество натуральных является их частью.

Множество натуральных чисел обозначается буквой N. Это множество имеет начало, но не имеет конца.

Еще существует расширенное множество N, где включается нуль.

Наименьшее натуральное число

В большинстве математических школ наименьшим значением N считается единица, так как отсутствие предметов считается пустотой.

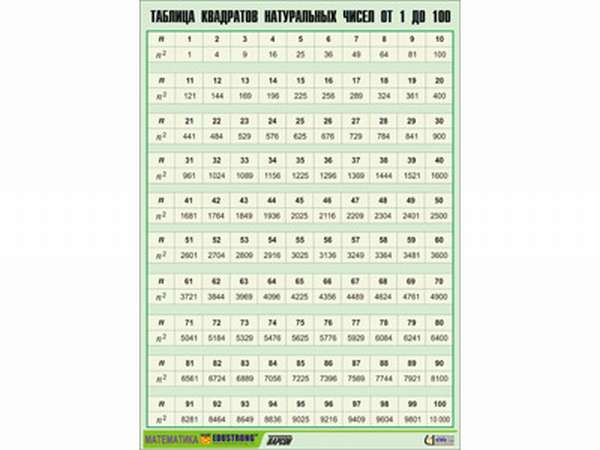
Но в иностранных математических школах, например во французской, нуль считается натуральным. Наличие в ряде нуля облегчает доказательство некоторых теорем.

Ряд значений N, включающий в себя нуль, называется расширенным и обозначается символом N0 (нулевой индекс).

Ряд натуральных чисел

N ряд – это последовательность всех N совокупностей цифр. Эта последовательность не имеет конца.

Особенность натурального ряда заключается в том, что последующее число будет отличаться на единицу от предыдущего, то есть возрастать. Но значения не могут быть отрицательными.

Внимание! Для удобства счета существуют классы и разряды:

Все N

Все N находятся во множестве действительных, целых, неотрицательных значений. Они являются их составной частью.

Эти значения уходят в бесконечность, они могут принадлежать классам миллионов, миллиардов, квинтиллионов и т.д.

Например:

Последовательность в N

В разных математических школах можно встретить два интервала, которым принадлежит последовательность N:

от нуля до плюс бесконечности, включая концы, и от единицы до плюс бесконечности, включая концы, то есть все положительные целые ответы.

N совокупности цифр могут быть как четными, так и не четными. Рассмотрим понятие нечетности.

Нечетные (любые нечетные оканчиваются на цифры 1, 3, 5, 7, 9.) при делении на два имеют остаток. Например, 7:2=3,5, 11:2=5,5, 23:2=11,5.

Что значит четные N

Любые четные суммы классов оканчиваются на цифры: 0, 2, 4, 6, 8. При делении четных N на 2, остатка не будет, то есть в результате получается целый ответ. Например, 50:2=25, 100:2=50, 3456:2=1728.

Важно! Числовой ряд из N не может состоять только из четных или нечетных значений, так как они должны чередоваться: за четным всегда идет нечетное, за ним снова четное и т.д.

Свойства N

Как и все другие множества, N обладают своими собственными, особыми свойствами. Рассмотрим свойства N ряда (не расширенного).

Внимание! Все вышеперечисленные неравенства действительны и в обратном направлении.

Как называются компоненты умножения

Во многих простых и даже сложных задачах нахождение ответа зависит от умения школьников умножать.

Для того, чтобы быстро и правильно умножать и уметь решать обратные задачи, необходимо знать компоненты умножения.

15.10=150. В данном выражении 15 и 10 являются множителями, а 150 – произведением.

Умножение обладает свойствами, которые необходимы при решении задач, уравнений и неравенств:

Например: 15.Х=150. Разделим произведение на известный множитель. 150:15=10. Сделаем проверку. 15.10=150. По такому принципу решаются даже сложные линейные уравнения (если упростить их).

Важно! Произведение может состоять не только из двух множителей. Например: 840=2.5.7.3.4

Что такое натуральные числа в математике?

Разряды и классы натуральных чисел

Вывод

Подведем итоги. N используются при счете или обозначении количества предметов. Ряд натуральных совокупностей цифр бесконечен, но он включает в себя только целые и положительные суммы разрядов и классов. Умножение тоже необходимо для того, чтобы считать предметы, а также для решения задач, уравнений и различных неравенств.

Это интересно! Легкие правила округления чисел после запятой

Источник