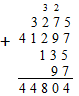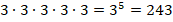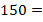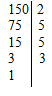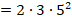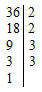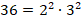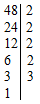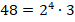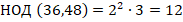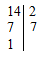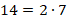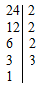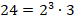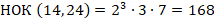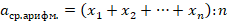Что такое натуральные цифры
Что такое Натуральное число
Определение натурального числа
Натуральные числа — это те числа, которые появились натуральным способом, когда считали сколько у человека есть предметов. Например: 1, 2, 3, 4, 5 и т. д.
Наибольшее натуральное число: не существует. Наименьшее натуральное число: 1.
Например, люди считали, сколько у них было фруктов: 1 яблоко, 3 апельсина, 2 дыни.
Нуль (0) не является натуральным числом, хотя некоторые области математики всё-таки считают 0 натуральным числом.
Отрицательные числа (–1, –3, –5. ) не являются натуральными числами («–3» яблок сложно посчитать физически).
Дроби (например, ⅓ или ⅖) тоже не являются натуральными числами.
Такие понятия, как отрицательные («–3»), дроби («⅓») и нуль («0») появились много позже.
Множество натуральных чисел
Множество натуральных чисел бесконечно и обозначается буквой N, т. е.:
Натуральные числа:
Натуральные числа с нулём:
Ряд натуральных чисел
Если записать все натуральные числа в порядке возрастания (каждое натуральное число отличается от предыдущего на 1), это будет ряд натуральных чисел. Но если какие-то числа будут отсутствовать, это уже не будет считаться рядом натуральных чисел. Например:
Наибольшего натурального числа не существует — натуральный ряд бесконечен.
Ненатуральные числа
Ненатуральные числа — это отрицательные и нецелые числа (обычно 0 тоже считается ненатуральным, но не всегда).
Отрицательные числа — это все те, которые ниже нуля, например: –1, –2, –3, –4, –5 и др.;
Свойства натуральных чисел
Натуральные числа обладают следующими свойствами:
Натуральные числа. Ряд натуральных чисел.
История натуральных чисел началась ещё в первобытные времена. Издревле люди считали предметы. Например, в торговле нужен был счет товара или в строительстве счет материала. Да даже в быту тоже приходилось считать вещи, продукты, скот. Сначала числа использовались только для подсчета в жизни, на практике, но в дальнейшем при развитии математики стали частью науки.
Натуральные числа – это числа которые мы используем при счете предметов.
Например: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, ….
Нуль не относится к натуральным числам.
Все натуральные числа или назовем множество натуральных чисел обозначается символом N.
Таблица натуральных чисел.
Натуральный ряд.
Натуральные числа, записанные подряд в порядке возрастания, образуют натуральный ряд или ряд натуральных чисел.
Свойства натурального ряда:
Пример №1:
Напишите первых 5 натуральных числа.
Решение:
Натуральные числа начинаются с единицы.
1, 2, 3, 4, 5
Пример №2:
Нуль является натуральным числом?
Ответ: нет.
Пример №3:
Какое первое число в натуральном ряду?
Ответ: натуральный ряд начинается с единицы.
Пример №4:
Какое последнее число в натуральном ряде? Назовите самое большое натуральное число?
Ответ: Натуральный ряд начинается с единицы. Каждое следующее число больше предыдущего на единицу, поэтому последнего числа не существует. Самого большого числа нет.
Пример №5:
У единицы в натуральном ряду есть предыдущее число?
Ответ: нет, потому что единица является первым числом в натуральном ряду.
Пример №6:
Назовите следующее число в натуральном ряду за числами: а)5, б)67, в)9998.
Ответ: а)6, б)68, в)9999.
Пример №7:
Сколько чисел находится в натуральном ряду между числами: а)1 и 5, б)14 и 19.
Решение:
а) 1, 2, 3, 4, 5 – три числа находятся между числами 1 и 5.
б) 14, 15, 16, 17, 18, 19 – четыре числа находятся между числами 14 и 19.
Пример №8:
Назовите предыдущее число за числом 11.
Ответ: 10.
Пример №9:
Какие числа применяются при счете предметов?
Ответ: натуральные числа.
Натуральные числа
Натуральные числа — одно из старейших математических понятий.
В далёком прошлом люди не знали чисел и, когда им требовалось пересчитать предметы (животных, рыбу и т.д.), они делали это не так, как мы сейчас.
Количество предметов сравнивали с частями тела, например, с пальцами на руке и говорили: «У меня столько же орехов, сколько пальцев на руке».
Со временем люди поняли, что пять орехов, пять коз и пять зайцев обладают общим свойством — их количество равно пяти.
Наибольшего натурального числа не существует.
При счёте число ноль не используется. Поэтому ноль не считается натуральным числом.
Затем появились и особые знаки для обозначения чисел — предшественники современных цифр. Цифры, которыми мы пользуемся для записи чисел, родились в Индии примерно 1 500 лет назад. В Европу их привезли арабы, поэтому их называют арабскими цифрами.
Натуральный ряд — это последовательность всех натуральных чисел:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 …
Натуральный ряд бесконечен, наибольшего натурального числа в нём не существует.
Десятичной потому, что 10 единиц каждого разряда образуют 1 единицу старшего разряда. Позиционной потому, что значение цифры зависит от её места в записи числа, то есть от разряда, в котором она записана.
Разряды и классы (включая класс миллионов) подробно разобраны на нашем сайте в материалах для начальной школы.
Класс миллиардов
Если взять десять сотен миллионов, то получим новую разрядную единицу — один миллиард или в записи цифрами.
1 000 миллионов = 1 000 000 000 = 1 млрд
Десять таких единиц — десять миллиардов, десять десятков миллиардов образуют следующую единицу — сто миллиардов.
Миллиарды, десятки миллиардов и сотни миллиардов образуют четвёртый класс — класс миллиардов.
Разряды и классы натурального числа
Рассмотрим натуральное число 783 502 197 048
| Название класса | Миллиарды | Миллионы | Тысячи | Единицы | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Название разряда | Сотни миллиардов | Десятки миллиардов | Миллиарды | Сотни миллионов | Десятки миллионов | Миллионы | Сотни тысяч | Десятки тысяч | Тысячи | Сотни | Десятки | Единицы |
| Цифра (символ) | 7 | 8 | 3 | 5 | 0 | 2 | 1 | 9 | 7 | 0 | 4 | 8 |
| Название класса | Миллиарды | Миллионы | Тысячи | Единицы | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Название разряда | Сотни миллиардов | Десятки миллиардов | Миллиарды | Сотни миллионов | Десятки миллионов | Миллионы | Сотни тысяч | Десятки тысяч | Тысячи | Сотни | Десятки | Единицы |
| Цифра (символ) | 7 | 8 | 3 | 5 | 0 | 2 | 1 | 9 | 7 | 0 | 4 | 8 |
C помощью таблицы разрядов прочитаем это число. Для этого надо слева направо по очереди называть количество единиц каждого класса и добавлять название класса.
Название класса единиц не произносят, также не произносят название класса, если все три цифры в его разрядах — нули.
Любое натуральное число можно записать в виде разрядных слагаемых.
Числа 1, 10, 100, 1000 … называются разрядными единицами. С их помощью натуральное число записывается в виде разрядных слагаемых. Так, например, число 307 898 будет выглядеть в виде разрядных слагаемых.
307 898 = 300 000 + 7 000 + 800 + 90 + 8
Проверить свои вычисления вы можете с помощью нашего калькулятора разложения числа на разряды онлайн.
Следующие за миллиардом классы названы в соответствии с латинскими наименованиями чисел. Каждая следующая единица содержит тысячу предыдущих.
Все числа пересчитать невозможно, поскольку за каждым числом следует число на единицу большее, но очень большие числа в повседневной жизни не нужны.
Однако, физики нашли число, которое превосходит количество всех атомов (мельчайших частиц вещества) во всей Вселенной.
Это число получило специальное название — гугол. Гугол — число, у которого 100 нулей.
Натуральные числа
Натуральные числа: определение, операции, свойства
Определение
Натуральными числами называются числа, предназначенные для счета предметов. Для записи натуральных чисел используются 10 арабских цифр (0–9), положенных в основание общепринятой для математических расчетов десятичной системы счисления.
Последовательность натуральных чисел
Иногда в ряд натуральных чисел вводят и 0. Это допустимо, и тогда говорят о расширенном натуральном ряде.
Классы натуральных чисел
Каждая цифра натурального числа выражает определенный разряд. Самая последняя – это всегда количество единиц в числе, предыдущая перед ней – количество десятков, третья от конца – количество сотен, четвертая – количество тысяч и так далее.
Для больших и очень больших чисел можно увидеть устойчивую тенденцию (если исследовать число справа налево, то есть от последней цифры к первой):
То есть всякий раз мы имеем дело с тремя цифрами, означающими единицы, десятки и сотни более крупного наименования. Такие группы формируют классы. И если с первыми тремя классами в повседневной жизни приходится иметь дело более или менее часто, то другие следует перечислить, потому что далеко не все помнят наизусть их названия.
Сложение натуральных чисел
Сложение натур.чисел представляет собой арифметическое действие, позволяющее получить число, в котором содержится столько же единиц, сколько имеется в складываемых числах вместе.
Знаком сложения является знак «+». Складываемые числа называются слагаемыми, получаемый результат – суммой.
Небольшие числа складывают (суммируют) устно, письменно такие действия записывают в строку.
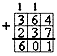
Если в столбик складывается не 2, а больше чисел, то при суммировании цифр разряда избыточным может оказаться не 1 десяток, а несколько. В этом случае на следующий разряд переносится количество таких десятков.
Вычитание натуральных чисел
Вычитание – это арифметическое действие, обратное сложению, которое сводится к тому, что по имеющейся сумме и одному из слагаемых нужно найти другое – неизвестное слагаемое. Число, из которого вычитают, называется уменьшаемым; число, которое вычитают, – вычитаемым. Результат вычитания называют разностью. Знак, которым обозначают действие вычитания, является «–».
При переходе к сложению вычитаемое и разность превращаются в слагаемые, а уменьшаемое – в сумму. Сложением обычно проверяют правильность выполненного вычитания, и наоборот.
Здесь 74 – уменьшаемое, 18 – вычитаемое, 56 – разность.
Обязательным условием при вычитании натуральных чисел является следующее: уменьшаемое обязательно должно быть больше вычитаемого. Только в этом случае полученная разность тоже будет натуральным числом. Если действие вычитания осуществляется для расширенного натурального ряда, то допускается, чтобы уменьшаемое было равно вычитаемому. И результатом вычитания в этом случае будет 0.
Примечание: если нулю равно вычитаемое, то операция вычитания не изменяет величины уменьшаемого.
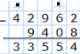
Вычитание многозначных чисел обычно производят в столбик. Записывают при этом числа так же, как и для сложения. Вычитание выполняется для соответствующих разрядов. Если же оказывается, что уменьшаемое меньше вычитаемого, то берут единицу из предыдущего (находящегося слева) разряда, которая после переноса, естественно, превращается в 10. Эту десятку суммируют с цифрой уменьшаемого данного разряда и после этого производят вычитание. Далее при вычитании следующего разряда обязательно учитывают, что уменьшаемое стало на 1 меньше.
Произведение натуральных чисел
Произведение (или умножение) натуральных чисел – это арифметическое действие, представляющее собой нахождение суммы произвольного количества одинаковых слагаемых. Для записи действия умножения используют знак «·» (иногда «×» или «*»). Например: 3·5=15.
Действие умножение незаменимо при необходимости складывать большое количество слагаемых. Например, если нужно число 4 прибавить 7 раз, то перемножить 4 на 7 проще, нежели выполнять такое сложение: 4+4+4+4+4+4+4.
Числа, которые перемножают, называются множителями, результат умножения – произведением. Соответственно, термин «произведение» может в зависимости от контекста выражать собой как процесс умножения, так и его результат.
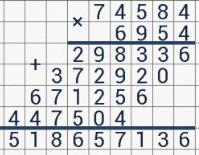
Многозначные числа перемножают в столбик. Для этого числа записывают так же, как и для сложения и вычитания. Рекомендуется первым (выше) записывать то из 2-х чисел, которое длиннее. В этом случае процесс умножения будет более простым, а следовательно, более рациональным.
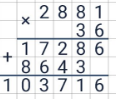
При умножении в столбик выполняют последовательное умножение цифры каждого из разрядов второго числа на цифры 1-го числа, начиная с его конца. Найдя первое такое произведение, записывают цифру единиц, а цифру десятков держат в уме. При умножения цифры 2-го числа на следующую цифру 1-го числа к произведению прибавляют ту цифру, которую держат в уме. И снова записывают цифру единиц полученного результата, а цифру десятков запоминают. При умножении на последнюю цифру 1-го числа полученное таким способом число записывают полностью.
Результаты умножения цифры 2-го разряда второго числа записывают вторым рядом, сместив его на 1 клетку вправо. И так далее. В итоге будет получена «лесенка». Все получившиеся ряды цифр следует сложить (по правилу сложения в столбик). Пустые клетки при этом нужно считать заполненными нулями. Полученная сумма и есть конечное произведение.
Примечание
Деление натуральных чисел
Делением называют арифметическое действие, с помощью которого по известному произведению и одному из множителей может быть найдет другой – неизвестный – множитель. Деление является действием, обратным умножению, и используется для проверки правильности выполненного умножения (и наоборот).
Число, которое делят, называют делимым; число, на которое делят, – делителем; результат деления называется частным. Знаком деления является «:» (иногда, реже – «÷»).
Здесь 48 – делимое, 6 – делитель, 8 – частное.
Не все натуральные числа можно поделить между собой. В этом случае выполняют деление с остатком. Заключается оно в том, что для делителя подбирается такой множитель, чтобы его произведение на делитель было бы числом, максимально близким по значению к делимому, но меньшим него. Делитель умножают на этот множитель и вычитают его из делимого. Разность и будет остатком от деления. Произведение делителя на множитель называют неполным частным. Внимание: остаток обязательно должен быть меньше подобранного множителя! Если остаток больше, то это означает, что множитель подобран неверно, и его следует увеличить.
где a – перемножаемое само на себя число, x – количество таких множителей.
Простые и составные натуральные числа
Всякое натуральное число, кроме 1, можно разделить как минимум на 2 числа – на единицу и на само себя. Исходя из этого критерия, натуральные числа разделяют на простые и составные.
Простыми считаются числа, которые делятся только на 1 и на само себя. Числа, которые делятся более чем на эти 2 числа, называют составными. Единица, делящаяся исключительно на саму себя, не относится ни к простым, ни к составным.
Простыми являются числа: 2,3,5,7,11,13,17,19 и т.д. Примеры составных чисел: 4 (делится на 1,2,4), 6 (делится на 1,2,3,6), 20 (делится на 1,2,4,5,10,20).
Всякое составное число можно разложить на простые множители. Под простыми множителями при этом понимаются его делители, являющиеся простыми числами.
Пример разложения на простые множители:
Делители натуральных чисел
Под делителем понимают число, на которое можно без остатка разделить данное число.
В соответствии с этим определением, простые натур.числа имеют 2 делителя, составные – больше 2 делителей.
Многие числа имеют общие делители. Общим делителем называется число, на которое данные числа делятся без остатка.
Особое значение имеет наибольший общий делитель (НОД). Это число, в частности, полезно уметь находить для сокращения дробей. Для его нахождения требуется разложить данные числа на простые множители и представить его как произведение их общих простых множителей, взятых в наименьших своих степенях.
Требуется найти НОД чисел 36 и 48.
Делимость натуральных чисел
Далеко не всегда представляется возможным «на глазок» определить, делится ли одно число на другое без остатка. В таких случаях полезным оказывается соответствующий признак делимости, то есть правило, по которому за считанные секунды можно определить, можно ли разделить числа без остатка. Для обозначения делимости используется знак «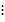
Наименьшее общее кратное
Эта величина (обозначается НОК) представляет собой наименьшее число, которое делится на каждое из заданных. НОК может быть найден для произвольного набора натуральных чисел.
НОК, как и НОД, имеет значительный прикладной смысл. Так, именно НОК нужно находить, приводя обыкновенные дроби к общему знаменателю.
НОК определяется путем разложения заданных чисел на простые множители. Для его формирования берется произведение, состоящее из каждого из встречающихся (хотя бы для 1 числа) простых множителей, представленных в максимальной степени.
Требуется найти НОК чисел 14 и 24.
Среднее арифметическое
Средним арифметических произвольного (но конечного) количества натуральных чисел является сумма всех этих чисел, разделенная на количество слагаемых:
Среднее арифметическое представляет собой некоторое усредненное значение для числового множества.
Даны числа 2,84,53,176,17,28. Требуется найти их среднее арифметическое.
Натуральные числа
Содержание
Определение натуральных чисел [ править ]
Неформальное определение [ править ]
| Определение: |
| Натура́льные чи́сла (англ. natural numbers, естественные числа) — числа, возникающие естественным образом при счёте (как в смысле перечисления, так и в смысле исчисления). |
Существуют два подхода к определению натуральных чисел — числа, используемые при:
Отрицательные и нецелые числа натуральными числами не являются.
Формальное определение [ править ]
Определить множество натуральных чисел позволяют аксиомы Пеано (англ. Peano axioms):
Теоретико-множественное определение [ править ]
Согласно теории множеств, единственным объектом конструирования любых математических систем является множество.
Таким образом, и натуральные числа вводятся, исходя из понятия множества, по двум правилам:
Числа, заданные таким образом, называются ординальными.
Первые несколько ординальных чисел и соответствующие им натуральные числа:
Классы эквивалентности этих множеств относительно биекций также обозначают [math]0, 1, 2, \dots.[/math]
Перечисленные аксиомы отражают наше интуитивные представления о «натуральном ряде».
Операции над натуральными числами [ править ]
Сложение [ править ]
Умножение [ править ]
Вычитание [ править ]
Деление чисел с остатком [ править ]
Формула деления с остатком: [math]n = m \cdot k + r,[/math] где [math]n\,[/math] — делимое, [math]m\,[/math] — делитель, [math]k\,[/math] — частное, [math]r\,[/math] — остаток, причем [math]0\leqslant r \lt b [/math]
Основная теорема арифметики [ править ]
Лемма Евклида [ править ]
Основная теорема арифметики [ править ]
Существование. Пусть [math]n[/math] — наименьшее натуральное число, неразложимое в произведение простых чисел. Оно не может быть единицей по формулировке теоремы. Оно не может быть и простым, потому что любое простое число является произведением одного простого числа — себя. Если [math]n[/math] составное, то оно — произведение двух меньших натуральных чисел. Каждое из них можно разложить в произведение простых чисел, значит, [math]n[/math] тоже является произведением простых чисел. Противоречие.
Принцип индукции, существование наименьшего числа в любом множестве натуральных чисел [ править ]
Индукция [ править ]
Формулировка принципа математической индукции:
Верность этого метода доказательства вытекает из так называемой аксиомы индукции, пятой из аксиом Пеано, которые определяют натуральные числа. Рассмотрение аксиом Пеано выходит за рамки этой статьи.
Также существует принцип полной математической индукции. Вот его строгая формулировка:
Существование наименьшего элемента [ править ]
Аксиому индукции можно заменить на аксиому существования минимума, и доказать аксиому индукции как теорему.
| Теорема (О существовании минимума): |