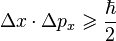Что такое наука механика
Механика
Полезное
Смотреть что такое «Механика» в других словарях:
МЕХАНИКА — (греч. mechanike, от mechane машина). Часть прикладной математики, наука о силе и сопротивлении в машинах; искусство применять силу к делу и строить машины. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. МЕХАНИКА… … Словарь иностранных слов русского языка
МЕХАНИКА — (от греч. mechanike (techne) наука о машинах, искусство построения машин), наука о механич. движении матер. тел и происходящих при этом вз ствиях между ними. Под механич. движением понимают изменение с течением времени взаимного положения тел или … Физическая энциклопедия
МЕХАНИКА — (от греч. mechane машина), наука о движении. До 17 века познания в этой области почти ограничивались эмпирическими наблюдениями, часто ошибочными. В 17 веке свойства движения впервые стали выводиться из немногих основных принципов математически.… … Большая медицинская энциклопедия
МЕХАНИКА — МЕХАНИКА, механики, мн. нет, жен. (греч. mechanike). 1. Отдел физики учение о движении и силах. Теоретическая и прикладная механика. 2. Скрытое, сложное устройство, подоплека, сущность чего нибудь (разг.). Хитрая механика. «Он, как говорят его… … Толковый словарь Ушакова
МЕХАНИКА — МЕХАНИКА, раздел физики, изучающий свойства тел (ВЕЩЕСТВ) под действием приложенных к ним сил. Делится на механику твердых и механику жидких тел. Другой раздел, статика, изучает свойства тел в состоянии покоя, а ДИНАМИКА движение тел. В статике… … Научно-технический энциклопедический словарь
механика — Наука о механическом движении и механическом взаимодействии материальных тел. [Сборник рекомендуемых терминов. Выпуск 102. Теоретическая механика. Академия наук СССР. Комитет научно технической терминологии. 1984 г.] Тематики теоретическая… … Справочник технического переводчика
МЕХАНИКА — [от греческого mechanike (techne) искусство построения машин], раздел физики, изучающий механическое движение твердых, жидких и газообразных материальных тел и взаимодействия между ними. В так называемой классической механике (или просто… … Современная энциклопедия
МЕХАНИКА — (от греч. mechanike искусство построения машин) наука о механическом движении материальных тел (т. е. изменении с течением времени взаимного положения тел или их частей в пространстве) и взаимодействиях между ними. В основе классической механики… … Большой Энциклопедический словарь
МЕХАНИКА — МЕХАНИКА, и, жен. 1. Наука о движении в пространстве и о силах, вызывающих это движение. Теоретическая м. 2. Отрасль техники, занимающаяся вопросами применения учения о движении и силах к решению практических задач. Строительная м. Прикладная м.… … Толковый словарь Ожегова
Механика — наука о движении. Изучая движение, механика необходимодолжна изучать и причины, производящие и изменяющие движения, называемыесилами; силы же могут и уравновешивать друг друга, и равновесие можетбыть рассматриваемо как частный случай движения.… … Энциклопедия Брокгауза и Ефрона
Механика — [от греческого mechanike (techne) искусство построения машин], раздел физики, изучающий механическое движение твердых, жидких и газообразных материальных тел и взаимодействия между ними. В так называемой классической механике (или просто… … Иллюстрированный энциклопедический словарь
Механика
Механика является одним из разделов физики. Под механикой обычно понимают классическую механику. Механика – наука, изучающая движение тел и происходящие при этом взаимодействия между ними.
В частности, каждое тело в любой момент времени занимает определенное положение в пространстве относительно других тел. Если со временем тело меняет положение в пространстве, то говорят, что тело движется, совершает механическое движение.
Механическим движением называется изменение взаимного положения тел в пространстве с течением времени.
Основная задача механики – определение положения тела в любой момент времени. Для этого нужно уметь кратко и точно указать, как движется тело, как при том или ином движении изменяется его положение с течением времени. Другими словами – найти математическое описание движения, т. е. установить сязи между величинами, характеризующими механическое движение.
При изучении движения материальных тел используют такие понятия, как:
Классическая механика основана на принципе относительности Галилея и законах Ньютона. Поэтому, ее еще называют – механикой Ньютона.
Механика изучает движение материальных тел, взаимодействия между материальными телами, общие законы изменения положений тел со временем, а также причины вызывающие эти изменения.
Общие законы механики подразумевают, что они справедливы при изучении движения и взаимодействия любых материальных тел (кроме элементарных частиц) от микроскопических размеров до объектов астрономических.
Механика включает в себя следующие разделы:
Следует отметить, что это не все разделы, которые входят в механику, но это основные разделы, которые изучает школьная программа. Кроме разделов указанных выше существует еще ряд разделов как имеющих самостоятельное значение, так и тесно связанных между собой и с указанными разделами.
Появление дополнительных разделов связано как с выходом за границы применимости классической механики (квантовая механика), так и с детальным изучением явлений происходящих при взаимодействии тел (например, теория упругости, теория удара).
Но, несмотря на это, классическая механика не теряет своего значения. Она является достаточной для описания в широком диапазоне наблюдаемых явлений без необходимости обращаться к специальным теориям. С другой стороны она проста для понимания и создает базу для других теорий.
Механика имеет большое значение для многих разделов астрономии, особенно для небесной механики (где изучаются движения планет, звезд и т. д.).
Особое значение механика имеет для техники. В гидродинамике, аэродинамике, динамике машин и механизмов, теории движения наземных, воздушных и транспортных средст используют уравнения и методы теоретической механики.
Механика
Содержание
Механическая система
Механика занимается изучением так называемых механических систем.
Механическая система обладает определённым числом 
степеней свободы, а её состояние описывается с помощью обобщённых координат 
и соответствующих им обобщённых импульсов 
. Задача механики состоит в изучении свойств механических систем, и, в частности, в выяснении их эволюции во времени.
Являясь одним из классов физических систем, механические системы по характеру взаимодействия с окружением разделяются на изолированные (замкнутые), закрытые и открытые, по принципу изменения свойств во времени — на статические и динамические.
Наиболее важными механическими системами являются:
Разделы механики
| Фундаментальные понятия |
|---|
| Пространство · Время · Масса · Сила Энергия · Импульс |
| Формулировки |
|---|
| Ньютоновская механика Лагранжева механика Гамильтонова механика Формализм Гамильтона — Якоби |
| Разделы |
|---|
| Прикладная механика Небесная механика Механика сплошных сред Геометрическая оптика Статистическая механика |
| Учёные |
|---|
| Галилей · Кеплер · Ньютон Эйлер · Лаплас · Д’Аламбер Лагранж · Гамильтон · Коши |
 Механика сплошных сред | ||||||||||
 | ||||||||||
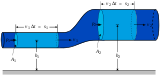| Сплошная среда | ||||||||||
| ||||||||||
| См. также: Портал:Физика |
| Квантовая механика |
|
| Эксперименты |
|---|
| Опыт Дэвиссона — Джермера · Опыт Поппера · Опыт Штерна — Герлаха · Опыт Юнга · Проверка неравенств Белла · Фотоэффект · Эффект Комптона |
| Формулировки |
|---|
| Представление Шрёдингера · Представление Гейзенберга · Представление взаимодействия · Матричная квантовая механика · Интегралы по траекториям · Диаграммы Фейнмана |
| Уравнения |
|---|
| Уравнение Шрёдингера · Уравнение Паули · Уравнение Клейна — Гордона · Уравнение Дирака · Уравнение фон Неймана · Уравнение Блоха · Уравнение Линдблада · Уравнение Гейзенберга |
| Интерпретации |
|---|
| Копенгагенская · Теория скрытых параметров · Многомировая |
| Развитие теории |
|---|
| Квантовая теория поля · Квантовая электродинамика · Теория Глэшоу — Вайнберга — Салама · Квантовая хромодинамика · Стандартная модель · Квантовая гравитация |
| Сложные темы |
|---|
| Квантовая теория поля · Квантовая гравитация · Теория всего |
| Известные учёные |
|---|
| Планк · Эйнштейн · Шрёдингер · Гейзенберг · Йордан · Бор · Паули · Дирак · Фок · Борн · де Бройль · Ландау · Фейнман · Бом · Эверетт |
Стандартные («школьные») разделы механики: кинематика, статика, динамика, законы сохранения. Кроме них, механика включает следующие (во многом перекрывающиеся) разделы:
Некоторые курсы механики ограничиваются только твёрдыми телами. Изучением деформируемых тел занимаются теория упругости (сопротивление материалов — её первое приближение) и теория пластичности. В случае, когда речь идёт не о жёстких телах, а о жидкостях и газах, необходимо прибегнуть к механике жидкостей и газов, основными разделами которой являются гидростатика и гидрогазодинамика. Общей теорией, изучающей движение и равновесия жидкостей, газов и деформируемых тел, является механика сплошных сред.
Основной математический аппарат классической механики: дифференциальное и интегральное исчисление, разработанное специально для этого Ньютоном и Лейбницем. К современному математическому аппарату классической механики относятся, прежде всего, теория дифференциальных уравнений, дифференциальная геометрия (симплектическая геометрия, контактная геометрия, тензорный анализ, векторные расслоения, теория дифференциальных форм), функциональный анализ и теория операторных алгебр, теория катастроф и бифуркаций. В современной классической механике используются и другие разделы математики. В классической формулировке, механика базируется на трёх законах Ньютона. Решение многих задач механики упрощается, если уравнения движения допускают возможность формулировки законов сохранения (импульса, энергии, момента импульса и других динамических переменных).
Различные формулировки механики
Все три закона Ньютона для широкого класса механических систем (консервативных систем, лагранжевых систем, гамильтоновых систем) связаны с различными вариационными принципами. В этой формулировке классическая механика таких систем строится на основе принципа стационарности действия: системы движутся так, чтобы обеспечить стационарность функционала действия. Такая формулировка используется, например, в лагранжевой механике и в гамильтоновой механике. Уравнениями движения в лагранжевой механике являются уравнения Эйлера — Лагранжа, а в гамильтоновой — уравнения Гамильтона.
Независимыми переменными, описывающими состояние системы в гамильтоновой механике, являются обобщённые координаты и импульсы, а в механике Лагранжа — обобщённые координаты и их производные по времени.
Если использовать функционал действия, определённый на реальной траектории системы, соединяющей некую начальную точку с произвольной конечной, то аналогом уравнений движения будут уравнения Гамильтона — Якоби.
Следует отметить, что все формулировки классической механики, основанные на голономных вариационных принципах, являются менее общими, чем формулировка механики, основанная на уравнениях движения. Не все механические системы имеют уравнения движения, представимые в виде уравнения Эйлера — Лагранжа, уравнения Гамильтона или уравнения Гамильтона — Якоби. Тем не менее, все формулировки являются как полезными с практической точки зрения, так и плодотворными с теоретической. Лагранжева формулировка оказалась особенно полезной в теории поля и релятивистской физике, а гамильтонова и Гамильтона — Якоби — в квантовой механике.
Классическая механика
Границы применимости классической механики
В настоящее время известно три типа ситуаций, в которых классическая механика перестаёт отражать реальность.
Механика
| Классическая механика |
|---|
 Второй закон Ньютона |
Энергия · Импульс
Лагранжева механика
Гамильтонова механика
Небесная механика
Механика сплошных сред
Геометрическая оптика
Статистическая механика
Эйлер · Лаплас · Д’Аламбер
Лагранж · Гамильтон · Коши
Меха́ника (греч. μηχανική — искусство построения машин) — техническая наука, выделившаяся из прикладной физики; наука о движении и силах, вызывающих движение. Предельными случаями механики являются небесная механика (механика движения небесных тел и гравитации) и квантовая механика (механика элементарных частиц и электромагнитного взаимодействия).
Содержание
Механическая система
Объекты, изучаемые механикой, называются механическими системами. Механическая система обладает определённым числом k степеней свободы и описывается с помощью обобщённых координат q1, … qk. Задача механики состоит в изучении свойств механических систем, и, в частности, в выяснении их эволюции во времени.
Наиболее важными механическими системами, в порядке увеличения сложности, являются:
Разделы механики
Математические основы
| Основа |
|---|
| Классическая механика · Постоянная Планка · Интерференция · Бра и кет · Гамильтониан · Старая квантовая теория |
| Фундаментальные понятия |
|---|
| Квантовое состояние · Квантовая наблюдаемая · Волновая функция · Квантовая суперпозиция · Квантовая запутанность · Смешанное состояние · Измерение · Неопределённость · Принцип Паули · Дуализм · Декогеренция · Теорема Эренфеста · Туннельный эффект |
| Эксперименты |
|---|
| Опыт Дэвиссона — Джермера · Опыт Поппера · Опыт Штерна — Герлаха · Опыт Юнга · Проверка неравенств Белла · Фотоэффект · Эффект Комптона |
| Формулировки |
|---|
| Представление Шрёдингера · Представление Гейзенберга · Представление взаимодействия · Матричная квантовая механика · Интегралы по траекториям · Диаграммы Фейнмана |
| Уравнения |
|---|
| Уравнение Шрёдингера · Уравнение Паули · Уравнение Клейна — Гордона · Уравнение Дирака · Уравнение Швингера — Томонаги · Уравнение фон Неймана · Уравнение Блоха · Уравнение Линдблада · Уравнение Гейзенберга |
| Интерпретации |
|---|
| Копенгагенская · Теория скрытых параметров · Многомировая · Теория де Бройля — Бома |
| Развитие теории |
|---|
| Квантовая теория поля · Квантовая электродинамика · Теория Глэшоу — Вайнберга — Салама · Квантовая хромодинамика · Стандартная модель · Квантовая гравитация |
| Сложные темы |
|---|
| Квантовая теория поля · Квантовая гравитация · Теория всего |
| Известные учёные |
|---|
| Планк · Эйнштейн · Шрёдингер · Гейзенберг · Йордан · Бор · Паули · Дирак · Фок · Борн · де Бройль · Ландау · Фейнман · Бом · Эверетт |
Стандартные («школьные») разделы механики:
Основной математический аппарат классической механики: дифференциальное и интегральное исчисление, разработанное специально для этого Ньютоном и Лейбницем. В классической формулировке, механика строится на трёх законах Ньютона. Решение многих задач механики упрощается, если ограничиться только потенциальным взаимодействием тел, поскольку в этом случае интегрирование уравнений движения приводит к закону сохранения энергии.
Лагранжева механика
Классическая механика
Границы применимости классической механики
В настоящее время известно три типа ситуаций, в которых классическая механика перестаёт отражать реальность.
Что такое наука механика
По поводу предмета механики уместно сослаться на слова авторитетного учёного-механика С. М. Тарга из введения к 4-му изданию его широко известного учебника теоретической механики: «Механикой в широком смысле этого слова называется наука, посвящённая решению любых задач, связанных с изучением движения или равновесия тех или иных материальных тел и происходящих при этом взаимодействий между телами. Теоретическая механика представляет собою часть механики, в которой изучаются общие законыдвижения и взаимодействия материальных тел, то есть те законы, которые, например, справедливы и для движения Земли вокруг Солнца, и для полёта ракеты или артиллерийского снаряда и т. п. Другую часть механики составляют различные общие и специальные технические дисциплины, посвящённые проектированию и расчёту всевозможных конкретных сооружений, двигателей, механизмов и машин или их частей (деталей)».
В приведённом высказывании упущен из виду тот факт, что изучением общих законов движения и взаимодействия материальных тел занимается также и механика сплошных сред (илимеханика сплошной среды) — обширная часть механики, посвящённая движению газообразных, жидких и твёрдых деформируемых тел. В этой связи академик Л. И. Седов отмечал: «В теоретической механике изучаются движения материальной точки, дискретных систем материальных точек и абсолютно твёрдого тела. В механике сплошной среды … рассматриваются движения таких материальных тел, которые заполняют пространство непрерывно, сплошным образом, и расстояния между точками которых во время движения меняются».
Таким образом, по предмету изучения механика подразделяется на:
Другой важнейший признак, используемый при подразделении механики на отдельные разделы, основан на тех представлениях о свойствах пространства, времени и материи, на которые опирается та или иная конкретная механическая теория. По данному признаку в рамках механики выделяют такие разделы:
Механическая система
Механика занимается изучением так называемых механических систем.
Механическая система обладает определённым числом 
степеней свободы, а её состояние описывается с помощью обобщённых координат 
и соответствующих им обобщённых импульсов 
. Задача механики состоит в изучении свойств механических систем, и, в частности, в выяснении их эволюции во времени.
Являясь одним из классов физических систем, механические системы по характеру взаимодействия с окружением разделяются на изолированные (замкнутые), закрытые и открытые, по принципу изменения свойств во времени — на статические и динамические.
Наиболее важными механическими системами являются:
Важнейшие механические дисциплины
| [показать] Фундаментальные понятия |
|---|
| [показать] Формулировки |
|---|
| [показать] Разделы |
|---|
| [показать] Учёные |
|---|
 Механика сплошных сред | |||||
 | |||||
| Сплошная среда | |||||
| |||||
| См. также: Портал:Физика |
| Квантовая механика | |||||||||
| |||||||||
| Принцип неопределённости | |||||||||
| Введение Математические основы | |||||||||
| |||||||||
| См. также: Портал:Физика |
Стандартные («школьные») разделы механики: кинематика, статика, динамика, законы сохранения. Кроме них, механика включает следующие (во многом перекрывающиеся по содержанию) механические дисциплины:
Некоторые курсы механики ограничиваются только твёрдыми телами. Изучением деформируемых тел занимаются теория упругости (сопротивление материалов — её первое приближение) и теория пластичности. В случае, когда речь идёт не о жёстких телах, а о жидкостях и газах, необходимо прибегнуть к механике жидкостей и газов, основными разделами которой являются гидростатика и гидрогазодинамика. Общей теорией, изучающей движение и равновесия жидкостей, газов и деформируемых тел, является механика сплошных сред.
Основной математический аппарат классической механики: дифференциальное и интегральное исчисление, разработанное специально для этого Ньютоном и Лейбницем. К современному математическому аппарату классической механики относятся, прежде всего, теория дифференциальных уравнений, дифференциальная геометрия (симплектическая геометрия, контактная геометрия, тензорный анализ, векторные расслоения, теория дифференциальных форм), функциональный анализ и теория операторных алгебр, теория катастроф и бифуркаций. В современной классической механике используются и другие разделы математики. В классической формулировке, механика базируется на трёх законах Ньютона. Решение многих задач механики упрощается, если уравнения движения допускают возможность формулировки законов сохранения (импульса, энергии, момента импульса и других динамических переменных).
Различные формулировки механики
Все три закона Ньютона для широкого класса механических систем (консервативных систем, лагранжевых систем, гамильтоновых систем) связаны с различными вариационными принципами. В этой формулировке классическая механика таких систем строится на основе принципа стационарности действия: системы движутся так, чтобы обеспечить стационарность функционала действия. Такая формулировка используется, например, влагранжевой механике и в гамильтоновой механике. Уравнениями движения в лагранжевой механике являются уравнения Эйлера — Лагранжа, а в гамильтоновой — уравнения Гамильтона.
Независимыми переменными, описывающими состояние системы в гамильтоновой механике, являются обобщённые координаты и импульсы, а в механике Лагранжа — обобщённые координаты и их производные по времени.
Если использовать функционал действия, определённый на реальной траектории системы, соединяющей некую начальную точку с произвольной конечной, то аналогом уравнений движения будут уравнения Гамильтона — Якоби.
Следует отметить, что все формулировки классической механики, основанные на голономных вариационных принципах, являются менее общими, чем формулировка механики, основанная на уравнениях движения. Не все механические системы имеют уравнения движения, представимые в виде уравнения Эйлера — Лагранжа, уравнения Гамильтона или уравнения Гамильтона — Якоби. Тем не менее, все формулировки являются как полезными с практической точки зрения, так и плодотворными с теоретической. Лагранжева формулировка оказалась особенно полезной в теории поля и релятивистской физике, а гамильтонова и Гамильтона — Якоби — в квантовой механике.
Классическая механика
Границы применимости классической механики
В настоящее время известно три типа ситуаций, в которых классическая механика перестаёт отражать реальность.