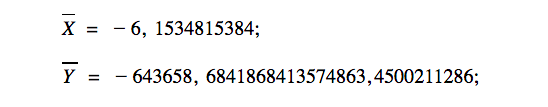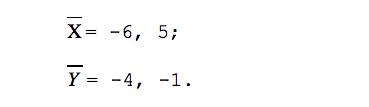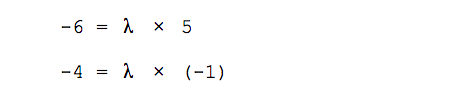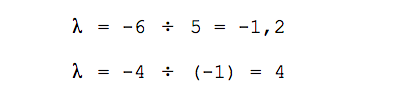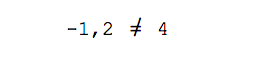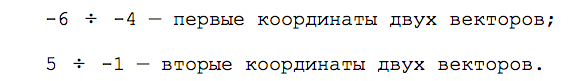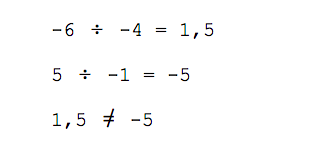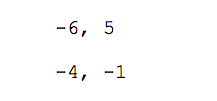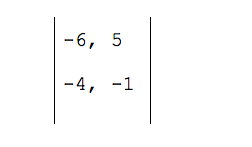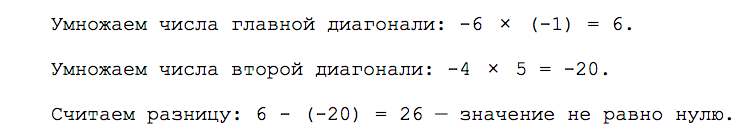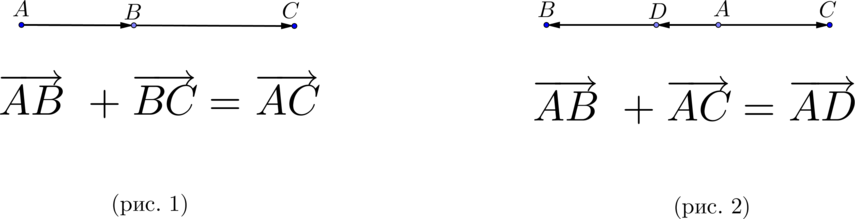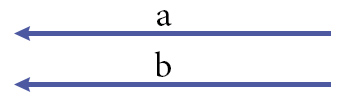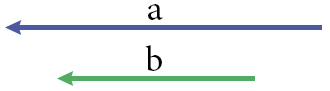Что такое неколлинеарные векторы в геометрии

Векторы: третий уровень сложности

Знакомимся с коллинеарностью.

Для большинства людей искусственный интеллект — это нечто сложное и таинственное. А для математиков это синоним фразы «перемножение матриц». С точки зрения человека, который владеет линейной алгеброй, в искусственном интеллекте нет ничего загадочного.

Мы хотим, чтобы вы тоже смогли понять искусственный интеллект на уровне математики. Для этого у нас идёт цикл статей про линейную алгебру:

Сама тема несложная, но конкретно этот шаг вам ничего не даст в практическом смысле. Но если вам хватит терпения, на базе этих знаний мы уже перейдём к матрицам.

Что за коллинеарность

Представьте два вектора, которые находятся в одной плоскости и располагаются параллельно друг другу. При этом у них может быть разная длина. Такое расположение делает связку векторов коллинеарными, или, по-простому, линейно зависимыми.

И наоборот: если вектора находятся в одной плоскости и располагаются не параллельно друг относительно друга, то их считают линейно независимыми — неколлинеарными. Пока что ничего сложного.

Коллинеарные векторы Неколлинеарные векторы

Сложение коллинеарных и неколлинеарных векторов

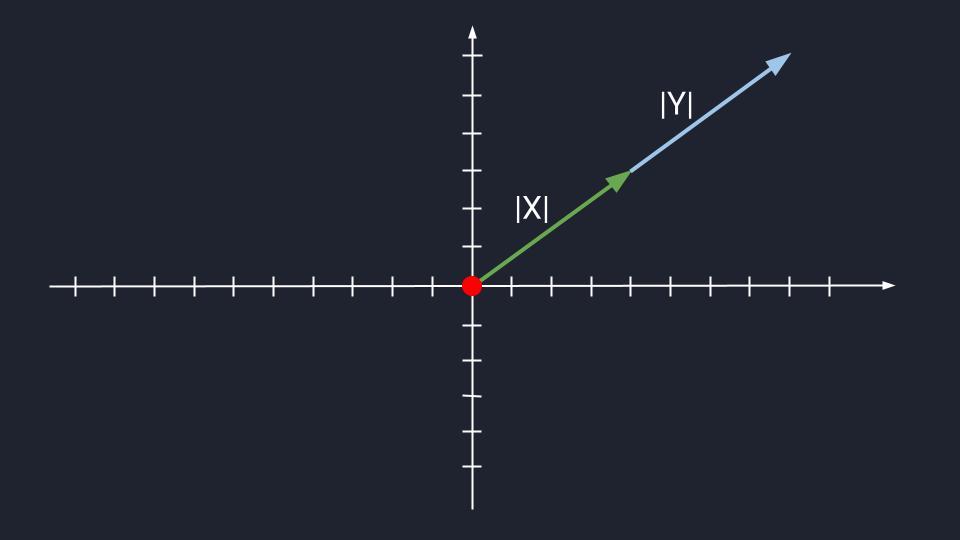
Очевидно, что сложить два коллинеарных вектора очень легко: откладываем второй вектор от начала первого, получится новый вектор. Он будет коллинеарным своим слагаемым, они все будут лежать, грубо говоря, на одной линии.

Можно представить, что вы идёте прямо: каждый ваш шаг — это вектор. Каждый новый шаг — новый вектор. Но если все их сложить, получится один большой прямой вектор длиной как все ваши шаги.

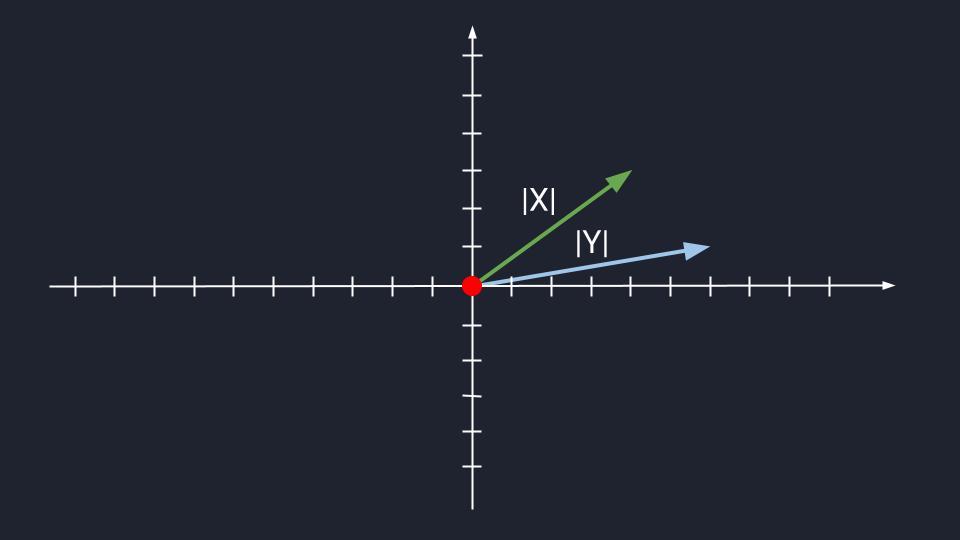
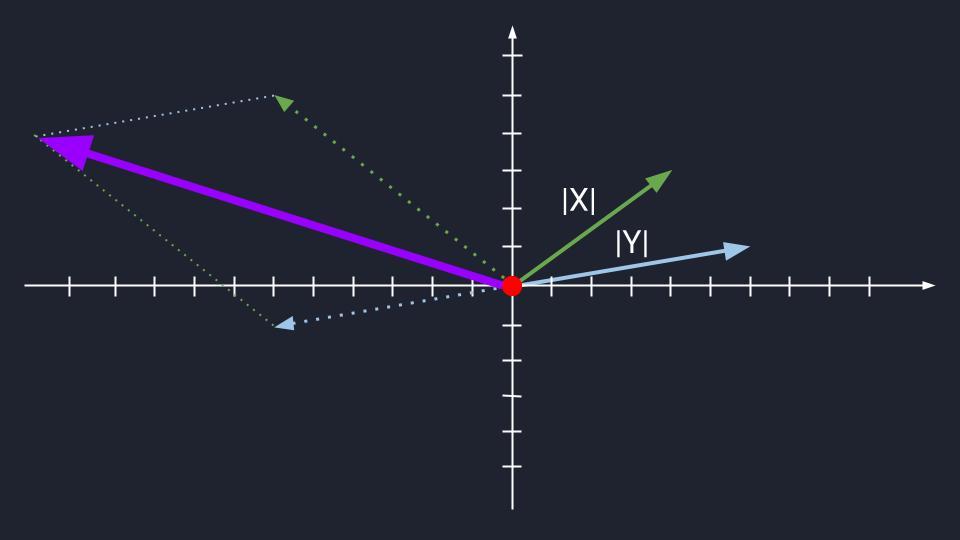
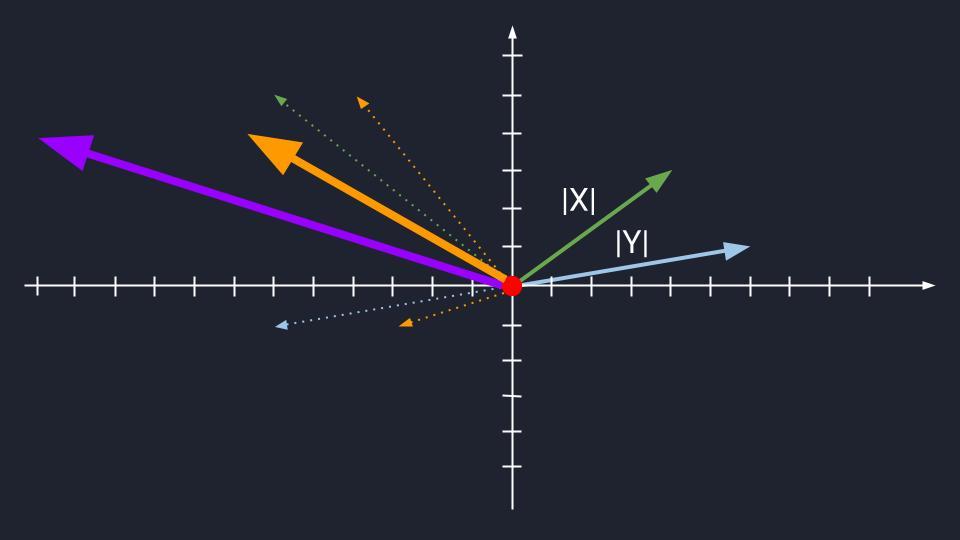
Теперь попробуем сложить пару неколлинеарных векторов. Это как если бы мы сначала сделали шаг немного правее, а потом сделали бы шаг влево. Шага два, но если соединить начало и конец пути, он не будет совпадать с траекториями наших шагов. Появится какой-то новый вектор, с новым направлением, и он будет неколлинеарным по отношению к своим слагаемым.

Также пару неколлинеарных векторов из одной плоскости можно растянуть и развернуть в пространстве. Если их сложить, также появится новый вектор.

У математиков такой вектор называют базисом. Когда базис находится на плоскости или в пространстве, то он может единственным образом превращаться обратно в пару неколлинеарных векторов, которые его сформировали.

Правило работает, когда мы масштабируем и меняем расположение векторов в пространстве. Если мы изменим направление исходных векторов, то получим новый базис.

Базис — понятие из высшей математики, поэтому, если сейчас сложно, не отчаивайтесь. Студенты-математики когда-то тоже отчаивались.

Мы изменили пару неколлинеарных векторов и сформировали из них базис — получили новый фиолетовый вектор с собственной системой координат Теперь мы изменили исходные неколлинеарные векторы и получили новый базис — это оранжевый вектор

Как определять неколлинеарность

Когда мы работаем с короткими векторами, всё очевидно: нарисовали систему координат, отложили на ней векторы, они либо совпали, либо не совпали. Если совпали — коллинеарные, если нет — неколлинеарные.

А теперь представьте, что вектора настолько огромные, что мы физически не можем их нарисовать и сопоставить. Например,

Как такое нарисовать? Как проверить коллинеарность? Вот тут начинается магия алгебры.

Есть три способа проверки линейной зависимости векторов. Для простоты вычислений проверим эти три способа на вот этих всё ещё простых векторах:

По этим координатам ответим на два вопроса: являются ли предложенные вектора линейно зависимыми (то есть коллинеарными) и можно ли их раскладывать по базису.

Первый способ. Запишем простую систему уравнений: возьмём первую координату каждого вектора и приравняем её ко второй координате каждого вектора, умноженной на неизвестное число λ. Вычислим λ и сравним результаты.

👉 Знак λ здесь по традиции и для удобства. На самом деле это просто некое неизвестное число. Вместо этой буквы могли быть X, Y, Z или N, но так как у нас вектора уже называются X и Y, а N в математике используется для других целей, возьмём λ — это греческая буква «лямбда», давний предок нашей русской буквы «Л».

Составляем систему уравнений:

Вычисляем значение λ:

Сравниваем результат и делаем вывод:

Мы получили разное значение для неизвестного числа λ и поэтому наши векторы будут считаться линейно независимыми. Из них можно получить базис.

Если бы значение λ совпало, то мы бы имели дело с линейно зависимыми векторами.

Второй способ. Проверяем координаты векторов на пропорциональность: берём первую координату первого вектора, делим её на первую координату второго вектора. Повторяем это же действие со вторыми координатами: берём вторую координату первого вектора и делим её на вторую координату второго вектора.

Получаем такую пропорцию:

Считаем значение и сравниваем результат:

Равенство не выполняется, и поэтому между векторами нет зависимости.

Третий способ. Используем четыре элемента наших координат для поиска определителя — скалярной величины, с которой мы подробно познакомимся в следующих статьях во время решения матричных уравнений. Сейчас нам не нужны подробности, и для проверки линейной зависимости достаточно формулы.

Записываем в две строки координаты наших векторов:

Переводим координаты векторов в определитель — добавляем с двух сторон вертикальную черту и получаем простую квадратную матрицу размером 2 на 2:

В полученной матрице две диагонали. Числа −6 и −1 образуют главную диагональ; числа −4 и 5 — вторую диагональ. Чтобы найти определитель, нам нужно умножить числа главной и второй диагонали, а затем вычесть их разницу.

Если из координат вектора мы получили определитель и он не равен нулю, то векторы считаются линейно независимыми и подходят для разложения по базису.

И наоборот: нулевой определитель указывает на линейную зависимость векторов.

Что из этого нужно запомнить

Что дальше

Следующий шаг — матрицы. Это те самые, которые лежат в основе всех нейронок и искусственного интеллекта. Матрица — это таблица чисел, с которыми можно проводить различные вычисления.

Источник

Векторы. Начальные сведения

Определения

Если длина вектора равна нулю (совпадают начало и конец), то такой вектор называют нулевым.

Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых ( \(\overrightarrow a, \overrightarrow b\) и \(\overrightarrow c\) ).

В противном случае векторы называются неколлинеарными (например, \(\overrightarrow a\) и \(\overrightarrow d\) ).

Векторы называются равными, если они сонаправлены и их длины равны.

Правила сложения коллинеарных векторов:

\(\blacktriangleright\) Для того, чтобы сложить два сонаправленных вектора, можно отложить второй вектор от конца первого. Тогда их сумма – вектор, начало которого совпадает с началом первого вектора, а конец – с концом второго (рис. 1).

\(\blacktriangleright\) Для того, чтобы сложить два противоположно направленных вектора, можно отложить второй вектор от начала первого. Тогда их сумма – вектор, начало которого совпадает с началом обоих векторов, длина равна разности длин векторов, направление совпадает с направлением большего по длине вектора (рис. 2).

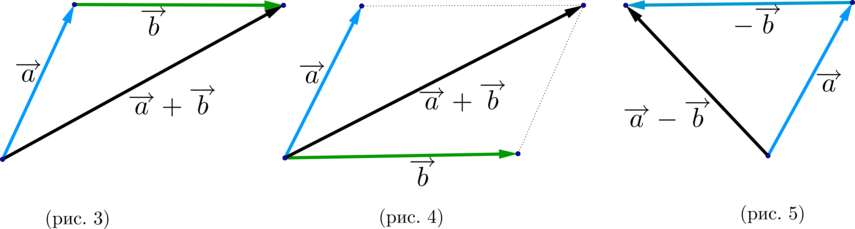
Правила сложения неколлинеарных векторов \(\overrightarrow \) и \(\overrightarrow\) :

\(\blacktriangleright\) Правило треугольника (рис. 3).

\(\blacktriangleright\) Правило параллелограмма (рис. 4).

Определение

Вектор \(\overrightarrow <-b>\) – это вектор, противоположно направленный с вектором \(\overrightarrow \) и совпадающий с ним по длине.

Свойства сложения векторов

Замечание

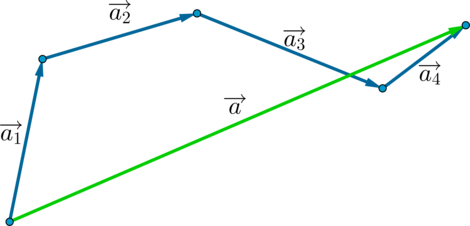
Для того, чтобы сложить несколько вектором, можно отложить их последовательно: каждый следующий от конца предыдущего. Тогда суммой этих векторов будет вектор, начало которого совпадает с началом первого вектора, а конец — с концом последнего: \[\overrightarrow +\overrightarrow +\overrightarrow + \overrightarrow =\overrightarrow \]

Определение

Свойства произведения вектора на число

1. Сочетательный закон: \(k(\lambda\overrightarrow )=(k\lambda)\overrightarrow \) ;

Теорема

Источник

Определение вектора

В статье пойдет речь о том, что такое вектор, что он из себя представляет в геометрическом смысле, введем вытекающие понятия.

Для начала дадим определение:

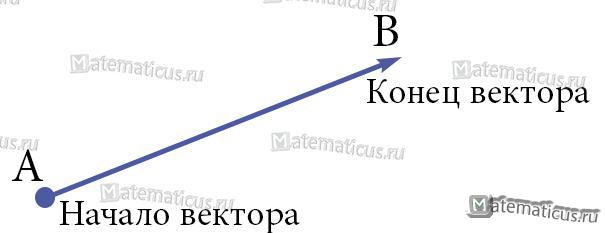
Вектор – это направленный отрезок прямой.

Исходя из определения, под вектором в геометрии отрезок на плоскости или в пространстве, который имеет направление, и это направление задается началом и концом.

Нулевой вектор

Под нулевым вектором 0 → будем понимать любую точку плоскости или пространства.

Из определения становится очевидным, что нулевой вектор может иметь любое направление на плоскости и в пространстве.

Длина вектора

Под длиной вектора A B → понимается число, большее либо равное 0, и равное длине отрезка АВ.

Понятия модуль вектора и длина вектора равносильны, потому что его обозначение совпадает со знаком модуля. Поэтому длину вектора также называют его модулем. Однако грамотнее использовать термин «длина вектора». Очевидно, что длина нулевого вектора принимает значение ноль.

Коллинеарность векторов

Два вектора лежащие на одной прямой или на параллельных прямых называются коллинеарными.

Два вектора не лежащие на одной прямой или на параллельных прямых называются неколлинеарными.

Следует запомнить, что Нулевой вектор всегда коллинеарен любому другому вектору, так как он может принимать любое направление.

Коллиниарные векторы в свою очередь тоже можно разделить на два класса: сонаправленные и противоположно направленные.

Направление векторов

Считается, что нулевой вектор является сонаправленым к любым другим векторам.

Равные и противоположные векторы

Равными называются сонаправленные вектора, у которых длины равны.

Противопожными называются противоположно направленные вектора, у которых их длины равны.

Введенные выше понятия позволяют нам рассматривать векторы без привязки к конкретным точкам. Иначе говоря, можно заменить вектор равным ему вектором, отложенным от любой точки.

Углы между векторами

Угол φ = ∠ A O B называется углом между векторами a → = O A → и b → = O B → .

Очевидно, что угол между сонаправленными векторами равен нулю градусам (или нулю радиан), так как сонаправленные векторы лежат на одной или на параллельных прямых и имеют одинаковое направление, а угол между противоположно направленными векторами равен 180 градусам (или π радиан), так как противоположно направленные векторы лежат на одной или на параллельных прямых, но имеют противоположные направления.

Перпендикулярными называются два вектора, угол между которыми равен 90 градусам (или π 2 радиан).

Источник

Понятие о векторе

Вектор (векторная величина) – всякая величина, обладающая направлением.

Скаляр (скалярная величина) – величина, не обладающая направлением.

А вот например температура есть скаляр, так как не связано c направлением. Масса, плотность, объём, площадь, время это тоже скаляр.

В аналитической геометрии направленный отрезок называется вектором.

Расстояние между началом и концом вектора называется длиной или модулем вектора. Модуль есть скалярная величина.

О единичном векторе см. здесь

Обозначение вектора

Модуль вектора обозначается двумя вертикальными чертами слева и справа:

Нуль-вектор

Если начало A и конец B отрезка AB совпадают, то отрезок AB обращается в точку и теряет направление. Этот вектор называется нуль-вектором и считается коллинеарным и сонаправленным с любым вектором. Обозначается, как число нуль (знак 0).

Любая точка пространства может рассматриваться как нуль-вектор.

Коллинеарные векторы

Коллинеарные векторы – это векторы, лежащие на параллельных прямых.

Неколлинеарные векторы – это векторы, не лежащие на параллельных прямых.

Другим словами параллельные вектора называются коллинеарными.

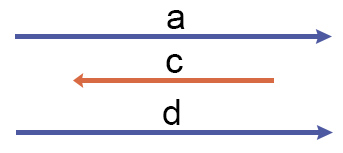
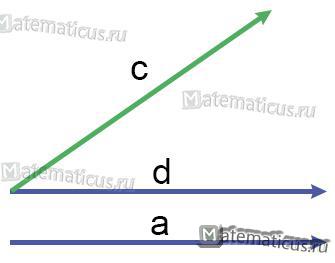
Векторы a, c, d – коллинеарны.

Векторы a и d – векторы имеющие одинаковое направление и их называют или сонаправленными или равнонаправленными векторами, а векторы a и c и векторы с и d называют противоположно направленными.

Компланарные векторы

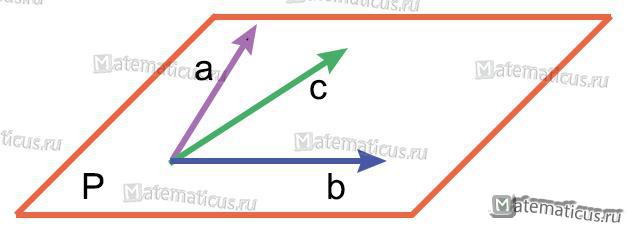
Компланарными векторами называют три вектора, которые лежат в одной плоскости или параллельны одной плоскости.

На этом рисунке векторы a,b,c являются компланарными

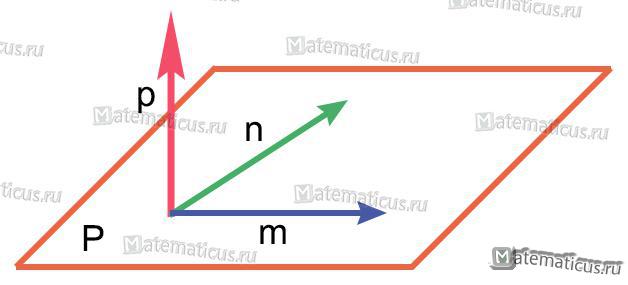
На рисунке векторы m,n,p — некомпланарны

Смешанное произведение трех компланарных векторов равно 0, т.е.

(a, b, c) = 0

Пример смешанного произведения трех компланарных векторов смотрите здесь

Равенство векторов

Два вектора a и b равны, если они равнонаправленные и имеют один и тот же модуль (длину).

На рисунке векторы a и b равны.

Векторы c и d не равны (даже если длины одинаковы), так как направления различны, следовательно и векторы c и a тоже не равны.

Векторы d и a равны.

Сонаправленные векторы

Сонаправленные векторы — это коллинеарные вектора, направленные в одну сторону, т.е. совпадают направления.

Обозначение: a↑↑b

Противоположные векторы

Два коллинеарных (параллельных) вектора, имеющие равные модули и противоположно направленные, т.е. друг другу называются противоположными векторами.

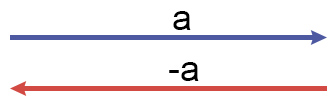
Вектор, противоположный вектору a, обозначается как –a.

Обозначение: a↑↓b

Векторы a и – a — противоположные.

Источник

Геометрия

Лучшие условия по продуктам Тинькофф по этой ссылке

Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера

. 500 руб. на счет при заказе сим-карты по этой ссылке

Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке

План урока:

Понятие вектора в пространстве

Напомним, что в курсе планиметрии мы уже подробно изучали вектора и действия с ними. При этом предполагалось, что все вектора располагаются в одной плоскости. Однако можно расширить понятие вектора так, чтобы они использовались и в стереометрии. В таком случае вектора уже могут располагаться в различных плоскостях.

Начнем с определения вектора:

Конец вектора обозначают с помощью стрелки. Посмотрим на рисунок:

Здесь показаны сразу три вектора:

У вектора АВ начало находится в точке А, а конец – в точке В. Аналогично у вектора С D точка С – это начало, а D – это конец. В обоих случаях начало и конец – это различные точки, поэтому АВ и CD именуют ненулевыми векторами. Если же начало и конец находятся в одной точке, например в Т, то получается нулевой вектор ТТ. Всякую точку в пространстве можно рассматривать как нулевой вектор:

Длина вектора АВ – это длина соответствующего ему отрезка АВ. Для обозначения длины используют квадратные скобки:

Естественно, что нулевой вектор имеет нулевую длину.

Далее напомним понятие коллинеарных векторов:

Коллинеарные вектора могут быть либо сонаправленными, либо противоположно направленными. Сонаправленные вектора находятся на сонаправленных лучах. Рассмотрим пример с кубом:

Здесь показаны вектора AD и ВС. Они сонаправленные, этот факт записывается так:

Вектора AD и FE располагаются на скрещивающихся прямых, поэтому они не коллинеарны. Их нельзя считать ни сонаправленными, ни противоположно направленными.

Сонаправленные вектора, имеющие одинаковую длину, именуются равными.

Рассмотрим несколько простейших задач.

Задание. В прямоугольном параллелепипеде АВС DA ₁ B ₁ C ₁ D ₁ известны три его измерения:

Решение. Для нахождения длин этих векторов достаточно вычислить длину отрезков СВ, DB и DB ₁. Проще всего вычислить СВ, ведь отрезки СВ и AD одинаковы как стороны прямоугольника АВ CD :

Вектора АМ и МВ также коллинеарны и имеют одинаковую длину, но они противоположно направлены, а потому равными не являются.

Операции над векторами

Такой метод сложения векторов именуется правилом треугольника. Если нужно сложить больше двух векторов, то используют правило многоугольника. В этом случае необходимо каждый следующий вектор откладывать от конца предыдущего. При этом в стереометрии вектора могут располагаться в различных плоскостях, то есть они на самом деле многоугольник не образуют:

Напомним, что в планиметрии существовали так называемые противоположные вектора. Есть они и в стереометрии:

Главное свойство противоположных векторов заключается в том, что в сумме они дают нулевой вектор:

Заметим, что для получения противоположного вектора достаточно поменять его начало и конец, то есть в записи вектора обозначающие его буквы надо просто записать в обратном порядке:

1) b и a будут коллинеарными векторами;

Если k – положительное число, то вектора a и b будут сонаправленными. Если же k a и b будут направлены противоположно.

Задание. Дан параллелепипед АВС D А₁В₁С₁ D ₁. Постройте вектор, который будет являться суммой векторов:

Решение. В каждом случае необходимо заменить один из векторов в сумме на другой равный ему вектор так, чтобы можно было применить правило треугольника.

В задании а) вектор А₁ D ₁ заменить равным ему вектором ВС. В итоге получится вектор АС.

В задании б) заменяем А D ₁ на вектор ВС₁. Также можно было бы заменить АВ на D ₁ C ₁. В обоих случаях сумма окажется равной АС₁.

В задании в) удобно DA заменить на C ₁В₁, тогда искомой суммой будет вектор С₁В.

В задании г) производим замену DD ₁ на равный ему вектор BB ₁. Тогда сумма DB и BB ₁– это вектор DB ₁.

В задании д) необходимо заменить ВС на В₁С₁. В итоге получаем вектор DC :

Решение. В случае а) сначала запишем очевидное равенство векторов, вытекающее из правило многоугольника:

Обратите внимание, что здесь у каждого следующего слагаемого начальная точка совпадает с конечной точкой предыдущего слагаемого, поэтому равенство и справедливо:

Однако по условию а) нам надо использовать другие вектора для выражения АВ. Мы можем просто заменить вектора CD и DB на противоположные:

Теперь можно составить и выражение для АВ:

Аналогично решаем и задания б) и в):

Задание. Р – вершина правильной шестиугольной пирамиды. Докажите, что сумма векторов, совпадающих с ребрами этой пирамиды и начинающихся в точке Р, в точности равна сумме векторов, которые совпадают с апофемами пирамиды и при этом также начинаются в точке Р.

Решение. Обозначим вершины буквами А₁, А₂, … А₆, а середины сторон шестиугольника, лежащего в основании, буквами Н₁, Н₂, … Н₆, как это показано на рисунке:

Нам надо показать, что сумма красных векторов равна сумме черных векторов:

Теперь отдельно построим правильный шестиугольник, лежащий, в основании пирамиды:

Ясно, что вектора, образованные сторонами этого шестиугольника, в сумме дают нулевой вектор (по правилу многоугольника):

Так как точки Н₁, Н₂, … Н₆ – середины сторона, то вектора Н₆А₆, Н₅А₅,…Н₁А₁ будут вдвое короче векторов А₁А₆, А₆А₅, … А₂А₁. При этом они находятся на одних прямых, поэтому справедливы равенства:

Таким образом нам удалось из верного равенства (3) доказать (2), из которого в свою очередь следует справедливость и (1), ч. т. д.

Задание. Упростите выражения:

Решение. Здесь надо просто применить законы сложения и умножения векторов, как это делалось и в курсе планиметрии. Сначала раскрываем скобки, а потом приводим подобные слагаемые:

Компланарные векторы

Если мы отложим несколько векторов от одной точки, то они либо будут находиться в одной плос-ти, либо располагаться в различных плос-тях. В первом случае их именуют компланарными векторами, а во втором – некомпланарными.

Любые два вектора будут компланарны, ведь при их откладывании от одной точки мы получаем две пересекающихся прямых, а через них всегда можно провести плос-ть. Однако если векторов более двух, то они могут быть как компланарны, так и некомпланарны.

Рассмотрим для примера параллелепипед:

Здесь вектора АС, АВ и АD компланарны, так как все они принадлежат одной грани (то есть плос-ти) АВСD. А вектора АВ, АD и АА₁ некомпланарны, ведь через них нельзя провести одну плос-ть.

Очевидно, что если из трех векторов любые два коллинеарны, то вся тройка векторов компланарна, ведь при откладывании векторов от одной точки коллинеарные вектора окажутся на одной прямой.

Существует признак компланарности векторов:

Напомним, что подразумевается под разложением вектора. Пусть есть вектора а, b и c. Если существуют такие числах и y, при которых выполняется равенство

то говорят, что вектор с разложен по векторам а и b, причем числа xи y называются коэффициентами разложения.

Докажем сформулированный признак. Пусть есть три вектора а, b и c, а также числа xи y, такие, что

Эти вектора находятся в одной плос-ти ОАВ. Теперь от той же точки О отложим вектора ха и уb, концы которых окажутся в точках А₁ и В₁:

Естественно, что вектора ОА₁ и ОВ₁ также окажутся в плос-ти ОАВ. Тогда и их сумма будет принадлежать этой плос-ти, а эта сумма как раз и есть вектор с:

В итоге получили, что а, b и с располагаются в одной плос-ти, то есть они компланарны.

Справедливо и обратное утверждение. Если вектора а, b и с компланарны, но а и b неколлинеарны, то вектор с можно разложить на вектора a и b. Это утверждение прямо следует из изученной в 9 классе теоремы о разложении векторов. Важно отметить, что коэффициенты такого разложения определяются однозначно.

Для сложения тройки некомпланарных векторов можно применить так называемое правило параллелепипеда. Если есть три некомпланарных вектора, то можно отложить их от одной точки О и далее построить параллелепипед, в котором эти вектора будут ребрами. Тогда диагональ этого параллелепипеда, выходящая из точки О, и будет суммой этих трех векторов:

Разложение вектора на некомпланарные вектора

Иногда вектор можно разложить не на два, а на три вектора. Выглядит такое разложение так:

Для доказательства рассмотрим три некомпланарных вектора а, bи c, а также произвольный вектор р. Отложим их от одной точки О. Обозначим концы этих векторов большими буквами А, В, С и Р:

Через ОВ и ОА можно провести некоторую плос-ть α. Точка С ей принадлежать не может, ведь ОА, ОВ и ОС – некомпланарные вектора. Проведем через Р прямую, параллельную ОС. Так как ОС пересекает α, то и параллельная ей прямая также пересечет α в некоторой точке Р₁. (Примечание. Если Р принадлежит α, то точки Р и Р₁ совпадут, то есть вектор Р₁Р будет нулевым).

Далее через точку Р₁ в плос-ти α проведем прямую, параллельную ОВ, которая пересечет ОА в точке Р₂. Заметим, что вектор ОР₂ находится на той же прямой, что и вектор ОА, то есть они коллинеарны, поэтому существует такое число х, что

Итак, мы показали, что у произвольного вектора p есть разложение на заранее заданные некомпланарные вектора. Осталось показать, что существует только одно такое разложение. Докажем это методом от противного. Пусть есть второе разложение с другими коэффициентами х₁, у₁ и z₁:

В правой части находятся три вектора, которые в сумме нулевой вектор. По правилу сложения векторов это означает, что эти вектора образуют треугольник, то есть находятся в одной плос-ти:

Значит, они компланарны. Тогда компланарны и вектора a, b и с, что противоречит условию теоремы. Значит, второго разложения р на заданные некомпланарные векторы не существует, ч. т. д.

Задание. АВСD и А₁В₁С₁D₁ – параллелограммы, располагающиеся в разных плос-тях. Докажите, что тройка векторов ВВ₁, СС₁ и DD₁ компланарна.

Решение. Сначала построим рисунок по условию задачи:

Для доказательства используем признак компланарности векторов. Для этого надо один из векторов, отмеченных на рисунке красным, разложить на два других вектора.

В результате нам удалось разложить СС₁ на вектора BB₁ и CC₁. Значит, эти три вектора коллинеарны.

Задание. В параллелепипеде АВСDA₁B₁C₁D₁ запишите разложение вектора BD₁ по векторам ВА, ВС и ВВ₁.

Решение. Сначала представим вектор BD₁ как сумму трех векторов:

Теперь заметим, что вектора С₁D₁ и ВА соответствуют ребрам параллелепипеда. Эти ребра одинаковы по длине и параллельны, поэтому и вектора будут равными. Аналогично равны вектора СС₁ и ВВ₁:

Задание. АВСD – тетраэдр, а точка К делит его ребро ВС пополам. Разложите вектор DK по векторам DA, AB и AC.

Решение. Сначала запишем очевидное выражение для вектора DK:

Задание. В точке М пересекаются медианы треугольника АВС, а О – произвольная точка в пространстве. Разложите вектор ОМ по векторам ОА, ОВ и ОС.

Решение. Медиану, проходящую через точку А, мы обозначим как АА₁, то есть А₁ – это середина отрезка ВС. Также буквой К обозначим середину ОВ:

Сначала разложим вектор ОА₁ на ОВ и ОС. Это можно сделать, ведь они компланарны. КА₁ – это средняя линия ∆ОСВ, поэтому КА₁||ОС и КА₁ вдвое короче ОС. Это значит, что

Так как АА₁ – медиана, то точка М делит ее в отношении 2:1. Отсюда вытекает следующее соотношение:

Только что решенная задача может быть использована и при решении другого, более сложного задания.

Задание. Докажите, что в параллелепипеде АВСDА₁В₁С₁D₁ плос-ти А₁ВD и СB₁D₁ делят диагональ АС₁ на три равных отрезка.

Решение. Обозначим точкой K точку пересечения медиан ∆А₁ВD. Тогда по формуле, выведенной в предыдущей задаче, мы получаем, что

Это соотношение означает, что вектора АК и АС₁ коллинеарны, поэтому они располагаются на одной прямой (они не могут находиться на параллельных прямых, ведь у них есть общая точка А). Значит, точка K принадлежит диагонали АС₁, и отрезок АК втрое короче диагонали.

Аналогично можно показать, что и

Из этого также вытекает, что М принадлежит диагонали АС₁, и МС₁ втрое короче АС₁. Значит, точки М и К делят диагональ на три равных отрезка, ч. т. д.

Сегодня мы расширили понятие векторов и научились их применять не только в планиметрических, но и в стереометрических задачах. При сохраняются все правила, по которым выполняются действия над векторами. Также в стереометрии появляется новое понятие компланарных и некомпланарых векторов.

Источник