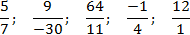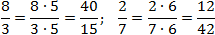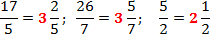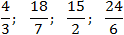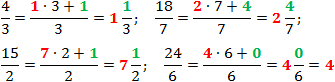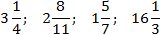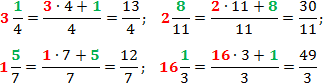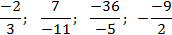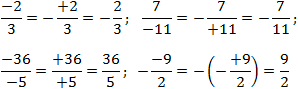Что такое неопределенная дробь
Что такое неопределенная дробь?
тем не менее, не определен ли наклон 0 4?
04 = 0 определено. 40 Не.
далее: 0 выше чего-то неопределенного?
тогда, что такое неопределенное число?
An математическое выражение, не имеющее смысла и не имеющее интерпретации. Например, в поле действительных чисел деление на ноль не определено. СМОТРИ ТАКЖЕ: неоднозначная, сложная бесконечность, направленная бесконечность, деление на ноль, неопределенное, неопределенное, четко определенное.
Что делает график неопределенным?
Неопределенный уклон (или бесконечно большой уклон) равен наклон вертикальной линии! Координата x никогда не меняется, независимо от координаты y! Нет пробега!
Какой пример неопределенного наклона?
Хороший пример неопределенного наклона из реальной жизни: Лифт поскольку лифт может двигаться только вверх или вниз. Он получил свое название «undefined» из-за того, что делить на ноль невозможно. … В общем, когда значения x или координаты x одинаковы для обеих точек, наклон не определен.
Как еще можно написать 0 4?
Как узнать, не определен ли уклон?
Неопределенный уклон (или бесконечно большой уклон) равен наклон вертикальной линии! Координата x никогда не меняется, независимо от координаты y! Нет пробега!
Определяется ли 0 делить на 3?
0 означает неопределенный уклон?
Как написать неопределенное число?
Обычно деление числа на ноль считается неопределенным. Часто обозначается словом UNDEF.
Что такое символ неопределенности?
Если a не входит в область определения f, то это записывается как f (а) ↑ и читается как «f (a) не определено». Я никогда не видел такого символа.
Каков пример неопределенного уклона?
Хороший пример неопределенного наклона из реальной жизни: Лифт поскольку лифт может двигаться только вверх или вниз. Он получил свое название «undefined» из-за того, что делить на ноль невозможно. Однако сделать 5/0 невозможно, потому что не существует числа, на которое можно умножить 0, чтобы получить 5.
Что такое пример неопределенного уклона?
Хороший пример неопределенного наклона из реальной жизни: Лифт поскольку лифт может двигаться только вверх или вниз. Он получил свое название «undefined» из-за того, что делить на ноль невозможно. … В общем, когда значения x или координаты x одинаковы для обеих точек, наклон не определен.
Что означает неопределенный?
Если a не входит в область определения f, то это записывается как f (а) ↑ и читается как «f (a) не определено».
Как вы строите неопределенный сюжет?
Как пишется неопределенный уклон?
Как записать неопределенный уклон в стандартной форме?
Что это значит, если наклон не определен?
Что такое 3/4 в виде десятичной дроби?
Ответ: 3/4 выражается как 0.75 в десятичной форме.
Что такое 4?
Ответ: В простейшем виде значение 4% в виде дроби равно 1/25. Пояснение: Преобразуем 4% в дробь в простейшем виде.
Как найти стандартную форму неопределенного склона?
Неопределенный наклон указывает на то, что у нас есть вертикальная линия, параллельная оси y и проходящая через все точки на плоскости с координатой x = constant (c) Уравнение записывается в виде х = с.
Что такое 5, разделенное на 3?
Как решить 7 разделить на 3?
Можно ли ноль делить на 1?
Ответ: Ноль, деленный на 1, равен 0.
Разделим ноль на 1. Пояснение:… 0/1 = 0, тогда как 1/0 не определено. Например, если ноль нужно разделить на любое число, это означает, что 0 элементов должны быть разделены или распределены между заданным количеством людей.
Что такое числовая дробь
Хотите почувствовать себя сапером? Тогда этот урок — для вас! Потому что сейчас мы будем изучать дроби — это такие простые и безобидные математические объекты, которые по способности «выносить мозг» превосходят весь остальной курс алгебры.
Главная опасность дробей состоит в том, что они встречаются в реальной жизни. Этим они отличаются, например, от многочленов и логарифмов, которые можно пройти и спокойно забыть после экзамена. Поэтому материал, изложенный в данном уроке, без преувеличения можно назвать взрывоопасным.
(или просто дробь) — это пара целых чисел, записанных через косую или горизонтальную черту.
Дроби, записанные через горизонтальную черту:
Те же самые дроби, записанные через косую черту:
5/7; 9/(−30); 64/11; (−1)/4; 12/1.
Обычно дроби записываются через горизонтальную черту — так с ними проще работать, да и выглядят они лучше. Число, записанное сверху, называется числителем дроби, а записанное снизу — знаменателем.
Любое целое число можно представить в виде дроби со знаменателем 1. получилась дробь из приведенного выше примера.
Вообще, в числитель и знаменатель дроби можно поставить любое целое число. Единственное ограничение — знаменатель должен быть отличен от нуля. Вспомните старое доброе правило: «На ноль делить нельзя!»
Если в знаменателе все-таки стоит ноль, дробь называется неопределенной. Такая запись не имеет смысла и не может участвовать в вычислениях.
Основное свойство дроби
Возникает резонный вопрос: как найти все дроби, равные данной? Ответ дадим в форме определения:
— числитель и знаменатель можно умножать на одно и то же число, отличное от нуля. При этом получится дробь, равная данной.
Это очень важное свойство — запомните его. С помощью основного свойства дроби можно упрощать и сокращать многие выражения. В будущем оно постоянно будет «всплывать» в виде различных свойств и теорем.
Неправильные дроби. Выделение целой части
Если числитель меньше знаменателя, такая дробь называется правильной. В противном случае (т.е. когда числитель больше или хотя бы равен знаменателю) дробь называется неправильной, и в ней можно выделить целую часть.
Целая часть записывается крупным числом спереди перед дробью и выглядит так (отмечена красным):
Чтобы выделить целую часть в неправильной дроби, надо выполнить три простых шага:
Ну как, сложно? На первый взгляд, может быть и сложно. Но стоит немного потренироваться — и вы будете делать это почти устно. А пока взгляните на примеры:
Задача. Выделите целую часть в указанных дробях:
Во всех примерах целая часть выделена красным цветом, а остаток от деления — зеленым.
Обратите внимание на последнюю дробь, где остаток от деления оказался равным нулю. Получается, что числитель полностью разделился на знаменатель. Это вполне логично, ведь 24 : 6 = 4 — суровый факт из таблицы умножения.
Если все делать правильно, числитель новой дроби обязательно будет меньше знаменателя, т.е. дробь станет правильной. Отмечу также, что лучше выделять целую часть в самом конце задачи, перед записью ответа. Иначе можно значительно усложнить вычисления.
Переход к неправильной дроби
Существует и обратная операция, когда мы избавляемся от целой части. Она называется переходом к неправильной дроби и встречается намного чаще, поскольку работать с неправильными дробями значительно проще.
Переход к неправильной дроби также выполняется в три шага:
Вот конкретные примеры:
Задача. Переведите в неправильную дробь:
Для наглядности целая часть снова выделена красным цветом, а числитель исходной дроби — зеленым.
Вынесение минуса за знак дроби
Рассмотрим случай, когда в числителе или знаменателе дроби стоит отрицательное число. Например:
В принципе, ничего криминального в этом нет. Однако работать с такими дробями бывает неудобно. Поэтому в математике принято выносить минусы за знак дроби.
Сделать это очень просто, если вспомнить правила:
Разумеется, эти правила можно применять и в обратном направлении, т.е. можно вносить минус под знак дроби (чаще всего — в числитель).
Случай «плюс на плюс» мы намеренно не рассматриваем — с ним, думаю, и так все понятно. Лучше посмотрим, как эти правила работают на практике:
Задача. Вынесите минусы из четырех дробей, записанных выше.
Обратите внимание на последнюю дробь: перед ней уже стоит знак минус. Однако он «сжигается» по правилу «минус на минус дает плюс».
Также не стоит перемещать минусы в дробях с выделенной целой частью. Эти дроби сначала переводят в неправильные — и лишь затем приступают к вычислениям.
Сократимые и несократимые дроби.
Дроби делятся на сократимые и несократимые дроби. Рассмотрим подробнее какую дробь называются сократимой и какую дробь называют несократимой.
Сократимая дробь, определение и примеры.
Определение:
Сократимая дробь – это дробь у которой числитель и знаменатель имеют общий положительный делитель не равный нулю и единице.
Например:
Докажите, что дробь \(\frac<20><35>\) является сократимой.
Решение:
Распишем числитель и знаменатель на простые множители, найдем их наибольший общий делитель (НОД).
20=2⋅2⋅5
35=5⋅7
Так как у числителя и знаменателя повторяется множитель 5, это число и будет их наибольшим общим делителем.
НОД(20, 35)=5
Сократим дробь на НОД.
Из сократимой дроби \(\frac<20><35>\) получили несократимую дробь \(\frac<4><7>\).
Несократимая дробь, определение и примеры.
Какие же дроби несократимые или что значит несократимая дробь? Ответ на вопрос кроется в определении.
Определение:
Несократимая дробь – это дробь у которой числитель и знаменатель имеют только один общий делитель равный единице, то есть числитель и знаменатель являются взаимно-простыми числами.
Рассмотрим пример:
Докажите, что дробь \(\frac<137><149>\) является несократимой дробью.
Решение:
Число 137 является простым, так как оно делиться на 1 и на само себя.
Число 149 является простым, так как оно делиться на 1 и на само себя.
У числителя 137 и знаменателя 149 нет общих делителей, поэтому дробь \(\frac<137><149>\) является несократимой.
Правило несократимой дроби.
Пример:
Запишите сократимую дробь в виде несократимой обыкновенной дроби \(\frac<55><100>\).
Решение:
По правилу несократимой дроби распишем числитель и знаменатель на простые множители.
55=5⋅11
100=5⋅2⋅2⋅5
Видим, что у числителя и знаменателя есть общий множитель равный 5, поэтому сокращаем дробь на 5.
Ответ: получили несократимую дробь \(\frac<11><20>\).
Неправильные сократимые и несократимые дроби.
Чтобы перевести неправильную сократимую дробь в неправильную несократимую дробь, мы пользуемся теми же правилами, что и для правильной сократимой дроби. Рассмотрим пример:
Запишите неправильную сократимую дробь в виде неправильной несократимой дроби \(\frac<32><20>\).
Решение:
Разложим числитель и знаменатель на простые множители.
32=2⋅2⋅2⋅2⋅2
20=5⋅2
Общий множитель у числителя и знаменателя равен 2. Распишем
Ответ: получили несократимую неправильную дробь \(\frac<16><5>\).
Вопросы по теме:
Как узнать сократима ли дробь?
Ответ: чтобы узнать сократима ли дробь для начала нужно расписать числитель и знаменатель на простые множители, а потом посмотреть если у них общие множители, если есть, то дробь сократима, иначе – несократима. Рассмотрим пример.
Определите сократима ли дробь \(\frac<16><25>\).
Решение:
Распишем числитель и знаменатель на простые множители.
16=2⋅2⋅2⋅2
25=5⋅5
Видно, что у числителя и знаменателя нет общих множителей (одинаковых множителей), следовательно, дробь несократима.
Пример:
Сколько несократимых правильных дробей: а) \(\frac<8><25>\) б) \(\frac<6><4>\) в) \(\frac<13><5>\) г) \(\frac<36><44>\).
Решение:
а) У числителя и знаменателя дроби \(\frac<8><25>\) (8=2⋅2⋅2, 25=5⋅5) нет общих множителей, поэтому это правильная несократимая дробь. По условию это дробь нам подходит.
б) У числителя и знаменателя дроби \(\frac<6><4>\) (6=2⋅3, 4=2⋅2, \(\frac<6><4>=\frac<2 \times 3><2 \times 2>=\frac<3><2>\) ) есть общий множитель равный 2, поэтому это дробь сократимая и еще неправильная, потому что числитель больше знаменателя. По условию задания эта дробь нам не подходит.
в) Числитель и знаменатель дроби \(\frac<13><5>\), 5 и 13 простые числа, поэтому общих множителей кроме 1 у них нет, дробь несократимая. Так как числитель больше знаменателя дробь неправильная, поэтому по условию задания нам она не подходит.
г) Числитель и знаменатель дроби \(\frac<36><44>\) (36=2⋅2⋅3⋅3, 44=2⋅2⋅11) имеют общий множитель равный 4, поэтому дробь \(\frac<36><44>=\frac<4 \times 9><4 \times 11>=\frac<9><11>\) является сократимой, правильной. Нам по условию задания не подходит.
Ответ: \(\frac<8><25>\) несократимая, правильная дробь.
Пример:
Сколько имеется правильных несократимых дробей со знаменателем: а) 145 б) 123 в) 133 г) 115.
Решение:
а) Распишем на простые множители знаменатель 145:
145=5⋅29
Нужно исключить все числа от 1 до 144 кратные 5 и 29.
На 5 делится: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100, 105, 110, 115, 120, 125, 130, 135, 140.
На 29 делится: 29, 58, 87, 116.
В сумме получаем 32 числа, которые имеют общий множитель с число 145. Всего у нас чисел 144.
144-32=112
Ответ: 112 правильных несократимых дробей со знаменателем 145.
б) Распишем на простые множители знаменатель 123:
123=3⋅41
В диапазоне чисел от 1 до 122 исключаем числа кратные 3 и 41.
На число 3 делится, поэтому не могут находиться в числителе: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99, 102, 105, 108, 111, 114, 117, 120.
На 41 делится: 41, 82.
В сумме получаем 40+2=42 числа, которые имеют общий множитель с число 123, поэтому мы их исключим. Всего у нас чисел 122.
122-42=80
Ответ: 80 правильных несократимых дробей со знаменателем 123.
в) Распишем на простые множители знаменатель 133:
133=7⋅19
Числа от 1 до 132 исключаем, они делятся на 7 и 19, для того чтобы получить все несократимые дроби от \(\frac<1><133>\) до \(\frac<132><133>\).
Число 7 кратно: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, 105, 112, 119, 126. Всего 18 чисел.
Число 19 кратно:19, 38, 57, 76, 95, 114. Всего 6 чисел.
132-18-6=108
Ответ: 108 правильных несократимых дробей со знаменателем 133.
г) Распишем на простые множители знаменатель 115:
115=5⋅23
Числа от 1 до 114 исключаем.
На 5 делится: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100, 105, 110. Всего 22 числа.
На 23 делится число: 23, 46, 96, 92. Всего 4 чисел.
114-22-4=88
Ответ: 88 правильных несократимых дробей со знаменателем 115.
Нестандартная задача по математике:
Когда нельзя сокращать сократимую обыкновенную дробь?
Ответ: когда сократимая обыкновенная дробь является номером углового дома или квартала.
Интегрирование рациональных дробей
Рациональной дробью называется дробь вида
Интегралы, содержащие в знаменателе квадратный трехчлен, можно вычислить, применяя прием выделения полного квадрата разности или суммы. Рассмотрим пример такого интеграла.
Алгоритм интегрирования рациональной дроби
1. Если дробь неправильная, надо выделить целую часть рациональной дроби, разделив числитель на знаменатель по правилу деления многочлена на многочлен, т.е. представить в виде:
2. Знаменатель разложим на простейшие сомножители: Qn(x)
3. Представим дробь
виде суммы простейших дробей с неопределенными коэффициентами.
Примеры интегрирования рациональных функций
Пример 4.
Корни знаменателя: x=1, а x 2 +1 = 0 не имеет действительных корней.
Тогда разложение для данной дроби имеет вид:
Приводя полученные дроби к общему знаменателю, получим тождество:
Вычислим коэффициенты разложения, приравнивая коэффициенты при одинаковых степенях. Так как знаменатель имеет три действительных различных корня, то три коэффициента найдем методом частных значений.
Подставим найденные коэффициенты в разложение и проинтегрируем дроби.
Какую дробь называют правильной в математике
Правильная дробь — что это такое в математике
Дробью в математике называют число, в состав которого входит одна либо несколько равных частей (или долей) от единицы.
Виды дробей в зависимости от формы записи:
Здесь число, которое расположено над чертой, является числителем. Под чертой расположен знаменатель. Числитель представляет собой делимое, а знаменатель играет роль делителя.
Правильная дробь — дробь с числителем, модуль которого меньше по сравнению с модулем знаменателя.
Неправильная дробь — дробь с числителем, модуль которого больше, чем модуль знаменателя, либо равен ему.
Любое число, которое является целым и не равно нулю, можно записать, как неправильную обыкновенную дробь. Знаменатель при этом будет равен 1.
Основное свойство дроби можно сформулировать таким образом: когда числитель и знаменатель, которые принадлежат одной дроби, умножают, либо делят на одно и то же число, дробь не поменяется, изменится лишь ее запись. К примеру:
1 5 = 1 × 2 5 × 2 = 2 10
Чем отличается правильная от неправильной и смешанной, как определить
Правильная дробь отличается тем, что имеет числитель, который меньше знаменателя.
В качестве наглядного примера можно записать правильные дроби:
Заметим, что во всех записанных случаях числитель меньше, чем знаменатель.
По сравнению с неправильной дробью правильная дробь всегда меньше 1. Тогда как неправильная дробь больше, либо равна 1.
Сравнение разных типов дробей:
Действия с правильными дробями, как найти
Правильные дроби можно встретить при решении множества задач по математике. Для них предусмотрены все действия, которые выполняют с обыкновенными дробями.
Приведение к общему знаменателю
Перед тем, как сравнить, сложить или вычесть дроби, требуется выполнить их преобразование. В результате арифметических действий дроби должны пробрести одинаковые знаменатели. К примеру, имеется пара дробей:
В результате знаменатели первой и второй дроби становятся одинаковыми и равными M. Допустимо заменить минимальное единое кратное при решении несложных примеров на какое-либо другое общее кратное. К примеру, таким кратным может стать произведение знаменателей.
Сравнение
С целью сравнения пары обыкновенных дробей необходимо выполнить операцию приведения их к единому знаменателю. Далее следует сравнить числители дробей, которые в итоге получились. Если числитель больше, то и дробь считается больше.
Далее необходимо привести дроби к знаменателю, равному 20.
3 4 = 15 20 ; 4 5 = 16 20
Сложение и вычитание
Прибавить одну обыкновенную дробь к другой обыкновенной дроби можно. Но перед этим требуется выполнить приведение этих дробей к единому знаменателю. После такой операции находят сумму числителей, а знаменатели оставляют без изменений.
1 2 + 1 3 = 3 6 + 2 6 = 5 6
НОК знаменателей для 2 и 3 составляет 6. Следует привести дробь 1 2 к знаменателю 6. Чтобы получить такой результат, необходимо выполнить умножение числителя и знаменателя на 3. В результате получим:
Затем требуется привести дробь 1 3 к аналогичному знаменателю. При этом нужно выполнить умножение числителя и знаменателя 2. Получим в итоге:
Похожий алгоритм действий предусмотрен для вычитания дробей. Перед тем, как посчитать их разность, следует привести дроби к общему знаменателю. Далее вычитают числители. Знаменатель при этом не меняется.
1 2 — 1 4 = 2 4 — 1 4 = 1 4
НОК знаменателей 2 и 4 составляет 4. Выполняя приведение дроби 1 2 к знаменателю 4, необходимо найти произведение числителя, знаменателя и числа 2. В результате получим:
Умножение и деление
При умножении двух обыкновенных дробей требуется выполнить умножение их числителей и знаменателей:
Рассмотрим частный случай умножения дроби на натуральное число. Для этого следует найти произведение числителя и данного числа, а знаменатель остается без изменений.
Когда числитель и знаменатель полученной дроби не являются взаимно простыми, необходимо такую дробь сократить:
5 8 · 2 5 = 10 40 = 1 4
В процессе деления одной обыкновенной дроби на другую требуется выполнить умножение первой дроби на дробь, которая является обратной для второй:
Возведение в степень и извлечение корня
Дроби можно возводить в степень. При этом необходимо выполнить арифметическое действие возведения в степень отдельно со знаменателем и числителем этой дроби:
2 3 3 = 2 3 3 3 = 8 27
Из дробей можно извлекать корень. Для того чтобы справиться с подобной задачей, необходимо извлечь заданный корень отдельно из числителя и знаменателя:
Перевод других видов дробей в правильную форму
Для того чтобы перевести неправильную дробь в правильную, либо для выполнения обратного действия, требуется соблюдать определенный порядок. Прямой перевод невозможен. Результатом подобной операции будет являться преобразованная запись, которая содержит в себе целую, а также дробную части. Последовательность действий:
С помощью достаточно простого метода удобно переводить числа из одной формы в какую-либо другую. Данный алгоритм можно записать в виде математического уравнения:
n a ÷ b = ( ( n × b ) + a ) ÷ b
Смешанное отношение представляет собой сумму из целого и части. Для того чтобы понять, как преобразовать дроби, следует выполнить сложение в качестве арифметического действия. В процессе первое слагаемое нужно записать в виде неправильной дроби путем деления целого на 1. Далее целесообразно воспользоваться правилом сложения дробей. Выполняется поиск общего знаменателя, дополнительных множителей, сложение в числителе. Формула имеет такой вид:
n a ÷ b = n ÷ 1 + a ÷ b = ( ( n × b ) + a ) ÷ b
Неправильную дробь превратить в обычную можно с помощью перевода ее в смешанную. В процессе выражение записывают в виде суммы натурального числа и правильной дроби:
Более простой способ преобразования дробей заключается в представлении делимого, как суммы дробей. При этом важно, чтобы при делении одной из них не было остатка:
m ÷ n = ( k + c ) ÷ n = k ÷ n + c ÷ n
Примеры задач с решением
В учебнике 100 листов. Ученик прочел ½ от общего количества страниц. Необходимо определить число листов, которые прочитал ученик.
Ответ: ученик прочитал 50 листов в учебнике.
Имеется емкость из стекла, наполненная водой, весом 550 гр. Половину воды вылили, а масса оставшейся составила 300 гр. Требуется рассчитать начальный вес воды и массу пустой емкости.
Значение массы воды, которую вылили:
250 гр. является половиной от всей воды, тогда вся вода весит:
Ответ: сначала в емкости было 500 гр. воды, массы емкости составляет 50 гр.
В кассе хранится сумма в 450 рублей. Необходимо определить количество денег в кассе после изъятия 1/3 от всей суммы.