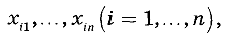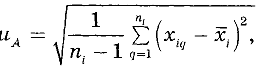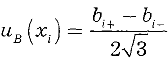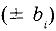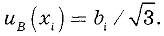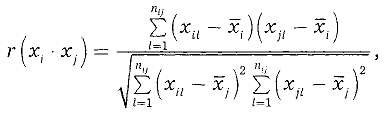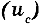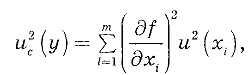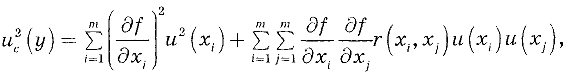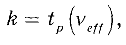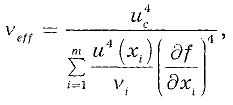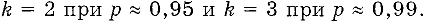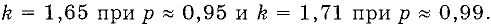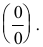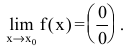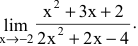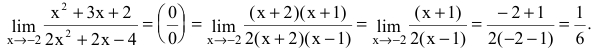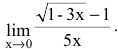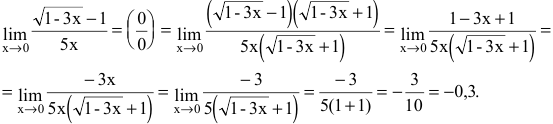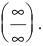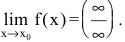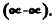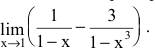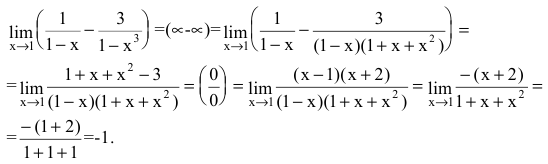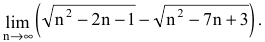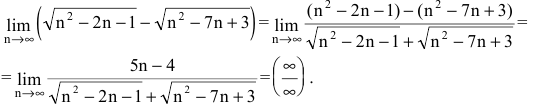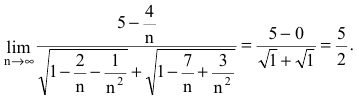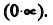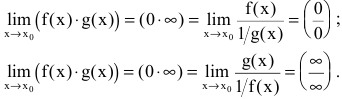Что такое неопределенность виды неопределенности

Неопределенность измерений в метрологии

Неопределенность измерений и ее отражение в описании результатов

Понятие «неопределенность», как наименование количественно оцениваемого свойства измерения, является относительно новым в метрологии. Термин «неопределенность» введен «Руководством по предоставлению неопределенности измерений» (далее «Руководство»), поскольку «погрешность» — идеализированное понятие, и не может быть известна точно.

Неопределенность (измерения) — это параметр, связанный с результатом измерения, характеризующий дисперсию значений, которые могли быть обоснованно приписаны измеряемой величине.

Руководство устанавливает общие правила оценивания и выражения неопределенности измерения, которые следует соблюдать при любых уровнях точности в широком спектре измерений, включая:

К оцениванию неопределенности следует приступать только после исключения результатов с грубыми погрешностями и исправления результатов измерений (исключения систематических составляющих погрешностей). Такой подход позволяет обоснованно применять математический аппарат теории вероятностей и математической статистики к «исправленным результатам измерений.

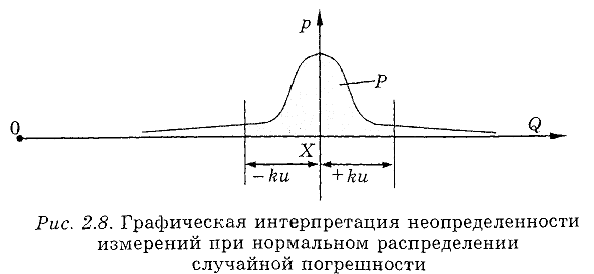
Неопределенность измерения в некоторых информационных источниках трактуется как мера возможной погрешности оцененного значения измеряемой величины, либо как оценка, характеризующая диапазон значений, в пределах которого находится истинное значение измеряемой величины. Под неопределенностью измерений фактически подразумевают то, что результат измерений фиксируется интервалом значений, а не конкретной точкой на числовой оси физической величины, при этом координата истинного значения остается неизвестной (неопределенной). В более широком смысле можно говорить также и о неопределенности «закона распределения» результатов многократных наблюдений при измерении конкретной физической величины. Графическое отображение неопределенности представлено на рис. 2.8.

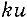
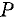
На рисунке отражены качественная оценка неопределенности (нормальное распределение), а также ее количественные оценки (расширенная неопределенность при выбранной доверительной вероятности ).

В руководстве используются следующие термины и определения:

Стандартная неопределенность — неопределенность результата измерения, выраженная как стандартное отклонение.

Оценка (неопределенности) по типу А — метод оценивания неопределенности путем статистического анализа рядов наблюдений.

Оценка (неопределенности) по типу В — метод оценивания неопределенности иным способом, чем статистический анализ рядов наблюдений.

Суммарная стандартная неопределенность — стандартная неопределенность результата измерения, когда результат получают из значений ряда других величин, равная положительному квадратному корню суммы членов, причем члены являются дисперсиями или ковариациями этих других величин, взвешенными в соответствии с тем, как результат измерения изменяется в зависимости от изменения этих величин.

Расширенная неопределенность — величина, определяющая интервал вокруг результата измерения, в пределах которого можно ожидать, находится большая часть распределения значений, которые с достаточным основанием могли быть приписаны измеряемой величине.

Коэффициент охвата — числовой коэффициент, используемый как множитель суммарной стандартной неопределенности для получения расширенной неопределенности. При нормальном распределении обычно применяют значения коэффициента охвата 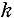, называемого также «коэффициент покрытия» в диапазоне от 2 до 3.

Установление связи между выбранным уровнем доверия и интервалом, характеризующим расширенную неопределенность, требует явных и неявных предположений относительно закона распределения вероятностей.

Классификация методов оценивания неопределенности на тип А и тип В представляет два различных способа получения оценки составляющих неопределенности. Оба типа основаны на вероятностном оценивании распределений случайных величин, а составляющие неопределенности при любом типе оценивания количественно представляют как оценки дисперсией или стандартных отклонений. Различия двух типов оценивания заключаются в методе получении оценки: прямое получение оценки путем статистического анализа рядов наблюдений (оценивание неопределенности по типу А) или получение оценки без непосредственного статистического анализа рядов наблюдений (оценивание неопределенности по типу В). Стандартную неопределенность при оценивании по типу В получают из предполагаемой функции плотности вероятностей, причем используют готовые оценки, полученные в ходе разнообразных метрологических мероприятий.

Наиболее распространенным способом формализации неполного знания о распределении величины является постулирование равновероятного распределения возможных значений этой величины в указанных границах.

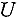
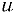
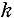
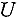
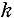
Расширенную неопределенность получают умножением суммарной стандартной неопределенности , на коэффициент охвата . Фактически представляет собой доверительный интервал, который с выбранной вероятностью накрывает истинное значение измеряемой величины. Коэффициент охвата зависит от вида приписанного распределения и выбранной доверительной вероятности.

По определению суммарная стандартная неопределенность измерения, представляет собой оценку среднего квадратического отклонения результата косвенных измерений, поскольку результат измерения получают из значений ряда других величин. Суммарную стандартную неопределенность при этом рассчитывают как значение квадратного корня из суммы дисперсий (или ковариаций) этих величин с учетом весовых коэффициентов.

Фактически понятие «суммарная стандартная неопределенность» следует рассматривать в двух вариантах:

Значения составляющих, входящих в суммарную неопределенность, могут быть получены путем оценивания как по типу А, так и по типу В, главное требование — под корнем эти составляющие должны быть представлены оценками соответствующих дисперсий.

Вычисление стандартной неопределенности по типу А

Исходными данными для вычисления являются результаты многократных измерений:

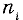
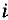
где — число измерений -й входной величины.

Стандартную неопределенность единичного измерения 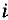-й входной величины вычисляют по формуле:

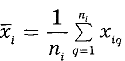
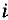
где — среднее арифметическое результатов измерений -й входной величины.

Стандартную неопределенность измерений 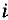-й входной величины, при которых результат определяют как среднее арифметическое, вычисляют по формуле:

Вычисление стандартной неопределенности 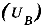по типу В

Исходными данными для вычисления является следующая информация:

-данные предшествовавших измерений величин, входящих в уравнение измерения; сведения о виде распределения вероятностей;

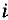
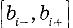
Неопределенности этих данных обычно представляют в виде границ отклонения значений величины от ее точечной оценки. При неполном знании о неопределенности некоторой -й входной величины обычно постулируют равновероятное распределение возможных значений этой величины в указанных (нижней и верхней) границах . При этом стандартную неопределенность, вычисляемую по типу В, определяют по формуле:

а для симметричных границ

В случае других законов распределения формулы для вычисления неопределенности по типу В будут иными.

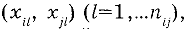
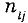
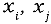
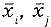
Для вычисления коэффициента корреляции используют согласованные пары результатов измерений где — число согласованных результатов измерений:

где — результаты прямых измерений, — средние значения результатов прямых измерений.

Вычисление суммарной стандартной неопределенности

В случае некоррелированных результатов измерений 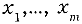оценку дисперсии суммарной стандартной неопределенности вычисляют по формуле:

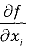
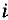
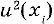
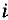
где — весовой коэффициент -ой стандартной неопределенности, — -ая стандартная неопределенность.

В случае коррелированных результатов измерений 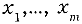оценку дисперсии суммарной стандартной неопределенности вычисляют по формуле:

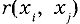
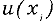
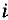
где — коэффициент корреляции; — стандартная неопределенность входной величины , вычисленная по типу А или по типу В.

Выбор коэффициента охвата 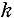при вычислении расширенной неопределенности

В общем случае коэффициент охвата выбирают в соответствии с формулой:

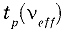
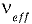
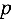
где — квантиль распределения Стьюдента с эффективным числом степеней свободы и доверительной вероятностью (уровнем доверия) .

Число степеней свободы определяют по формуле:

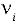
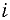
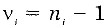
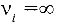
где — число степеней свободы при определении оценки -й входной величины: — для вычисления неопределенностей по типу A; — для вычисления неопределенностей по типу В.

Во многих практических случаях при вычислении неопределенностей измерений делают предположение о нормальном законе распределения возможных значений измеряемой величины и полагают:

При допущении распределения данных по закону равной вероятности полагают:

При представлении результатов измерений Руководство рекомендует приводить достаточное количество информации для возможности проанализировать или повторить весь процесс получения результата измерений и вычисления неопределенностей измерений, а именно:

Эта лекция взята со страницы лекций по нормированию точности:

Возможно эти страницы вам помогут:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Классификация неопределенностей измерений

Аналогично погрешностям, неопределенности измерений могут быть классифицированы по различным признакам.

По способу выражения их подразделяют на абсолютные и относительные.

Абсолютная неопределенность измерения— неопределенность измерения, выраженная в единицах измеряемой величины.

Относительная неопределенность результата измерений— отношение абсолютной неопределенности к результату измерений.

• неопределенность, оцениваемая по типу А (неопределенность типа А)— неопределенность, которую оценивают статистическими методами,

• неопределенность, оцениваемая по типу Б (неопределенность типа Б)— неопределенность, которую оценивают не статистическими методами.

Соответственно предлагается и два метода оценивания:

На первый взгляд, кажется, что это нововведение заключается лишь в замене существующих терминов известных понятий другими. Действительно, статистическими методами можно оценить только случайную погрешность, и поэтому неопределенность типа А — это то, что ранее называлось случайной погрешностью. Аналогично, НСП можно оценить только на основе априорной информации, и поэтому между неопределенностью по типу Б и НСП также имеется взаимно однозначное соответствие.

Однако, введение этих понятий является вполне разумным. Дело в том, что при измерениях по сложным методикам, включающим большое количество последовательно выполняемых операций, необходимо оценивать и учитывать большое количество источников неопределенности конечного результата. При этом их деление на НСП и случайные может оказаться ложно ориентирующим. Приведем два примера.

Пример 1. Существенную часть неопределенности аналитического измерения может составить неопределенность определения калибровочной зависимости прибора, являющаяся НСП в момент проведения измерений. Следовательно, ее необходимо оценивать на основе априорной информации нестатистическими методами. Однако во многих аналитических измерениях основным источником этой неопределенности является случайная погрешность взвешивания при приготовлении калибровочной смеси. Для повышения точности измерений можно применить многократное взвешивание этого стандартного образца и найти оценку погрешности этого взвешивания статистическими методами. Этот пример показывает, что в некоторых измерительных технологиях в целях повышения точности результата измерения ряд систематических составляющих неопределенности измерений может быть оценен статистическими методами, т. е. являться неопределенностями типа А.

Пример 2. По ряду причин, например, в целях экономии производственных затрат, методика измерения предусматривает проведение не более трех однократных измерений одной величины. В этом случае результат измерений может определяться как среднее арифметическое, мода или медиана полученных значений, но статистические методы оценивания неопределенности при таком объеме выборки дадут очень грубую оценку. Более разумным представляется априорный расчет неопределенности измерения по нормируемым показателям точности СИ, т. е. ее оценка по типу Б. Следовательно, в этом примере, в отличие от предыдущего, неопределенность результата измерений, значительная часть которой обусловлена влиянием факторов случайного характера, является неопределенностью типа Б.

Вместе с тем, традиционное разделение погрешностей на систематические, НСП и случайные также не теряет своего значения, поскольку оно точнее отражает другие признаки: характер проявления в результате измерения и причинную связь с эффектами, являющимися источниками погрешностей.

Таким образом, классификации неопределенностей и погрешностей измерений не являются альтернативными и взаимно дополняют друг друга.
В Руководстве имеются и некоторые другие терминологические нововведения. Ниже приведена сводная таблица терминологических отличий концепции неопределенности от классической теории точности.

Термины — примерные аналоги концепции неопределенности и классической теории точности

Новые термины, указанные в этой таблице, имеют следующие определения.

3. Вероятность охвата— вероятность, которой, по мнению экспериментатора, соответствует расширенная неопределенность результата измерений.
Примечания.

4. Коэффициент охвата — коэффициент, зависящий от вида распределения неопределенности результата измерений и вероятности охвата и численно равный отношению расширенной не­определенности, соответствующей заданной вероятности охвата, к стандартной неопределенности.

5. Число степеней свободы— параметр статистического распределения, равный числу независимых связей оцениваемой статистической выборки.

Источник

Раскрытие неопределенностей вида

Пусть

Пример №1

Вычислить предел

Решение:

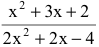
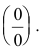
Числитель и знаменатель дроби при х=-2 обращаются в нуль. Имеем неопределенность вида Для ее раскрытия разложим числитель и знаменатель дроби на множители, а затем применим теоремы о пределах частного, суммы и произведения:

Пример №2

Вычислить предел

Решение:

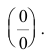
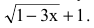
Имеем неопределенность вида Избавимся от иррациональности в числителе, умножив и разделив дробь на сопряженное к числителю выражение Получим:

В остальных случаях для раскрытия неопределенности вида 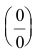используют первый замечательный предел или эквивалентные бесконечно малые функции.

Раскрытие неопределенностей вида

Пусть

Пример №3

Вычислить предел 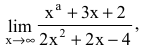если 1) а=2; 2) а=1; 3) а=4.

Решение:

Замечание. Для раскрытия неопределенностей вида 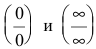используют также правило Лопиталя.

Раскрытие неопределенностей вида

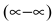
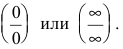
Неопределенное выражение вида преобразуется к неопределенности вида Методику раскрытия такой неопределенности покажем на примерах.

Пример №4

Вычислить предел

Решение:

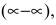
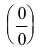
Имеем неопределенность вида которая преобразуется к неопределенности вида приведением функции к общему знаменателю:

Пример №5

Вычислить предел последовательности

Решение:

Для раскрытия неопределенности вида 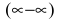умножим и разделим выражение в скобках на сопряженное:

Получили неопределенность вида 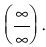Раскроем ее, разделив все члены полученного выражения на n:

Раскрытие неопределенностей вида

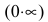
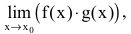
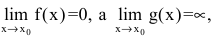
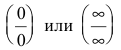
Неопределенное выражение вида получается при нахождении пределов вида где и сводится к неопределенности вида следующим образом:

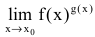
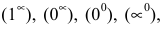
Замечание. При вычислении пределов показательно-степенных функций могут получиться неопределенности вида для раскрытия которых используют второй замечательный предел или правило Лопиталя.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник