Что такое неопределенность знания об исходе некоторого события как определяется единица
Что такое неопределенность знания об исходе некоторого события как определяется единица
Урок 6. Содержательный (вероятностный) подход к измерению информации
Измерение информации. Содержательный подход
 |  |
 |  |
Неопределенность знания — это количество возможных вариантов ответа на интересовавший вас вопрос. Еще можно сказать: возможных исходов события. Здесь событие — например, выборы мэра; исход — выбор, например, Н. Н. Никитина.
Сообщение, уменьшающее неопределенность знания об исходе некоторого события в два раза, несет 1 бит информации.
Согласно этому определению, сообщение в первой из описанных ситуаций несет 1 бит информации, поскольку из двух возможных вариантов ответа был выбран один.
Следовательно, количество информации, полученное во второй и в третьей ситуациях, больше, чем один бит. Но как измерить это количество?
Рассмотрим еще один пример.
Ученик написал контрольную по информатике и спрашивает учителя о полученной оценке. Оценка может оказаться любой: от 2 до 5. На что учитель отвечает: «Угадай оценку за два вопроса, ответом на которые может быть только «да» или «нет»». Подумав, ученик задал первый вопрос: «Оценка выше тройки?». «Да», — ответил учитель. Второй вопрос: «Это пятерка?». «Нет», — ответил учитель. Ученик понял, что он получил четверку. Какая бы ни была оценка, таким способом она будет угадана!
Первоначально неопределенность знания (количество возможных оценок) была равна четырем. С ответом на каждый вопрос неопределенность знания уменьшалась в 2 раза и, следовательно, согласно данному выше определению, передавался 1 бит информации.
Узнав оценку (одну из четырех возможных), ученик получил 2 бита информации.
Рассмотрим еще один частный пример, а затем выведем общее правило.
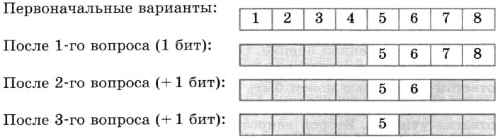
Вы едете на электропоезде, в котором 8 вагонов, а на вокзале вас встречает товарищ. Товарищ позвонил вам по мобильному телефону и спросил, в каком вагоне вы едете. Вы предлагаете угадать номер вагона, задав наименьшее количество вопросов, ответами на которые могут быть только слова «да» или «нет».
Немного подумав, товарищ стал спрашивать:
— Номер вагона больше четырех?
— Номер вагона больше шести?
— Ну теперь все ясно! Ты едешь в пятом вагоне!
Схематически поиск номера вагона выглядит так:
Каждый ответ уменьшал неопределенность знания в два раза. Всего было задано три вопроса. Значит, в сумме набрано 3 бита информации. То есть сообщение о том, что вы едете в пятом вагоне, несет 3 бита информации.
Способ решения проблемы, примененный в примерах с оценками и вагонами, называется методом половинного деления: ответ на каждый вопрос уменьшает неопределенность знания, имеющуюся перед ответом на этот вопрос, наполовину. Каждый такой ответ несет 1 бит информации.
Заметим, что решение подобных проблем методом половинного деления наиболее рационально. Таким способом всегда можно угадать, например, любой из восьми вариантов за 3 вопроса. Если бы поиск производился последовательным перебором: «Ты едешь в первом вагоне?» «Нет», «Во втором вагоне?» «Нет» и т. д., то про пятый вагон вы смогли бы узнать после пяти вопросов, а про восьмой — после восьми.
«Главная формула» информатики
Сформулируем одно очень важное условие, относящееся к рассмотренным примерам. Во всех ситуациях предполагается, что все возможные исходы события равновероятны. Равновероятно, что учитель может быть мужчиной или женщиной; равновероятен любой исход футбольного матча, равновероятен выбор одного из четырех кандидатов в мэры города. То же относится и к примерам с оценками и вагонами.
Обозначим буквой N количество возможных исходов события, или, как мы это еще называли, — неопределенность знания. Буквой i будем обозначать количество информации в сообщении об одном из N результатов.
В примере с учителем: N = 2, i = 1 бит;
в примере с оценками: N = 4, i = 2 бита;
в примере с вагонами: N = 8, i = 3 бита.
Нетрудно заметить, что связь между этими величинами выражается следующей формулой:
2 i = N. Действительно: 2 1 = 2 ; 2 2 = 4 ; 2 3 = 8.
С полученной формулой вы уже знакомы из курса информатики для 7 класса и еще не однажды с ней встретитесь. Значение этой формулы столь велико, что мы назвали ее главной формулой информатики. Если величина N известна, a i неизвестно, то данная формула становится уравнением для определения i. В математике такое уравнение называется показательным уравнением.
Пример. Вернемся к рассмотренному выше примеру с вагонами. Пусть в поезде не 8, а 16 вагонов. Чтобы ответить на вопрос, какое количество информации содержится в сообщении о номере искомого вагона, нужно решить уравнение:
Количество информации i, содержащееся в сообщении об одном из N равновероятных исходов некоторого события, определяется из решения показательного уравнения:
Пример. В кинозале 16 рядов, в каждом ряду 32 места. Какое количество информации несет сообщение о том, что вам купили билет на 12-й ряд, 10-е место?
Решение задачи: в кинозале всего 16 • 32 = 512 мест. Сообщение о купленном билете однозначно определяет выбор одного из этих мест. Из уравнения 2 i = 512 = 29 получаем: i = 9 битов.
Но эту же задачу можно решать иначе. Сообщение о номере ряда несет 4 бита информации, так как 2 4 = 16. Сообщение о номере места несет 5 битов информации, так как 2 5 = 32. В целом сообщение про ряд и место несет: 4 + 5 = 9 битов информации.
Данный пример иллюстрирует выполнение закона аддитивности количества информации (правило сложения): количество информации в сообщении одновременно о нескольких результатах независимых друг от друга событий равно сумме количеств информации о каждом событии отдельно.
Сделаем одно важное замечание. С формулой 2 i = N мы уже встречались, обсуждая алфавитный подход к измерению информации (см. § 3). В этом случае N рассматривалось как мощность алфавита, a i — как информационный вес каждого символа алфавита. Если допустить, что все символы алфавита появляются в тексте с одинаковой частотой, т. е. равновероятно, то информационный вес символа i тождественен количеству информации в сообщении о появлении любого символа в тексте. При этом N — неопределенность знания о том, какой именно символ алфавита должен стоять в данной позиции текста. Данный факт демонстрирует связь между алфавитным и содержательным подходами к измерению информации.
Формула Хартли
Если значение N равно целой степени двойки (4, 8, 16, 32, 64 и т. д.), то показательное уравнение легко решить в уме, поскольку i будет целым числом. А чему равно количество информации в сообщении о результате матча «Динамо»-«Зенит»? В этой ситуации N = 3. Можно догадаться, что решение уравнения
будет дробным числом, лежащим между 1 и 2, поскольку 2 1 = 2 2 = 4 > 3. А как точнее узнать это число?
В математике существует функция, с помощью которой решается показательное уравнение. Эта функция называется логарифмом, и решение нашего уравнения записывается следующим образом:
Читается это так: «логарифм от N по основанию 2». Смысл очень простой: логарифм по основанию 2 от N — это степень, в которую нужно возвести 2, чтобы получить N. Например, вычисление уже известных вам значений можно представить так:
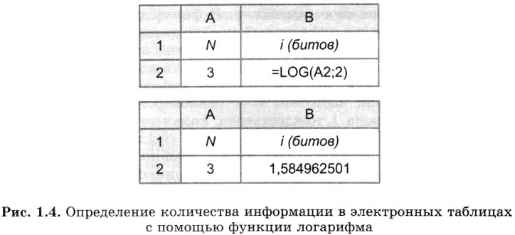
Значения логарифмов находятся с помощью специальных логарифмических таблиц. Также можно использовать инженерный калькулятор или табличный процессор. Определим количество информации, полученной из сообщения об одном исходе события из трех равновероятных, с помощью электронной таблицы. На рисунке 1.4 представлены два режима электронной таблицы: режим отображения формул и режим отображения значений.
Рис. 1.4. Определение количества информации в электронных таблицах с помощью функции логарифма
В табличном процессоре Microsoft Excel функция логарифма имеет следующий вид: LOG(apryмент; основание). Аргумент — значение N находится в ячейке А2, а основание логарифма равно 2. В результате получаем с точностью до девяти знаков после запятой: i = log23 = 1,584962501 (бита).
Формула для измерения количества информации: i = log2N была предложена американским ученым Ральфом Хартли (1888-1970) — одним из основоположников теории информации.
Формула Хартли:
Здесь i — количество информации, содержащееся в сообщении об одном из N равновероятных исходов события.
Данный пример показал, что количество информации, определяемое с использованием содержательного подхода, может быть дробной величиной, в то время как информационный объем, вычисляемый путем применения алфавитного подхода, может иметь только целочисленное значение.
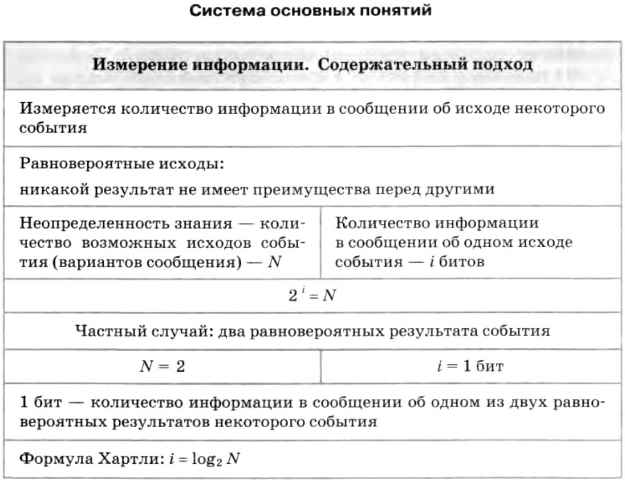
Система основных понятий
Вопросы и задания
а) на шестигранном игральном кубике выпала цифра 3;
б) в следующем году ремонт в школе начнется в феврале;
в) я приобрел абонемент в бассейн на среду;