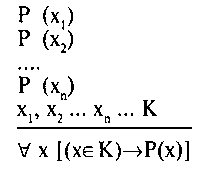Что такое неполная индукция

Полная и неполная индукция

Общее в природе и обществе не существует самостоятельно, до и вне единичного, а единич­ное не существует без общего; общее существует в единичном, через единичное, то есть проявля­ется в конкретных предметах. Поэтому общее, существенное, повторяющееся и закономерное в предметах познается через изучение единичного, и одним из средств такого познания выступает индукция.

Индуктивное умозаключение — это такая форма абстрактного мышления, в которой мысль развивается от знания меньшей степени общно­сти к знанию большей степени общности, а за­ключение, вытекающее из посылок, носит пре­имущественно вероятностный характер.

В зависимости от характера исследования различают полную и неполную индукцию.

Например, установление того, что каждый из документов, необходимых для оценки готовности уголовного дела для передачи в суд, имеется, позво­ляет с полным основанием делать вывод, что дело следует передавать в суд

Полная индукция дает достоверное знание, так как заключение делается только о тех предметах или явлениях, которые перечислены в посылках. Но область применения полной индукции весьма ограничена.

Полную индукцию можно применить, когда появляется возможность иметь дело с замкнутым классом предметов, число элементов в котором яв­ляется конечным и легко обозримым. Она предполагает наличие следующих условий: а) точное знание числа предметов или явлений, подлежащих изу­чению; б) убеждение, что признак принадлежит каждому элементу класса; в) небольшое число элементов изучаемого класса; г) целесообразность и рациональность.

Вот почему полная индукция чаще всего используется при расследова­нии уголовных дел, связанных с недостачей материальных ценностей. Здесь вывод осуществляется на основе подсчета всех без исключения содержащих­ся на складе или в хранилище предметов путем инвентаризации.

Однако в большинстве случаев юристу приходится иметь дело с такими однородными фактами, количество которых не ограничено или которые не все доступны в настоящее время для непосредственного изучения. Вот поче­му в таких случаях прибегают к использованию неполной индукции, кото­рая на практике применяется значительно шире, чем полная.

Неполная индукция часто применяется в реальной жизни, так как позво­ляет делать заключения на основе анализа определенной части данного класса предметов, экономит время и силы человека. Правда, в этом случае мы получим вероятностное заключение, которое в зависимости от вида не­полной индукции будет колебаться от менее вероятностного к более вероят­ностному.

По способам обоснования заключения различают следующие виды не­полной индукции: популярную и научную.

В популярной индукции на основе повторяемости одного и того же при­знака у некоторой части однородных предметов и при отсутствии противо­речащего случая делается общее заключение, что все предметы этого рода oбладают этим признаком. Степень вероятности истинного заключения в популярной индукции невысока, так как неизвестно, почему дело обстоит так, а не иначе.

Эффективность популярной индукции во многом зависит от того, на­сколько число случаев, закрепленных в посылках, по возможности будет: а) больше, б) разнообразнее, в) типичнее.

Научной индукцией называется умозаключение, в посылках которого наряду с повторяемостью признака у некоторых явлений класса содержится ин­формация о зависимости этого признака от определенных свойств явления.

Источник

Глава XIX. Об индукции

В предыдущей главе мы окончили рассмотрение того вида умозаключения, который называется дедукцией и который представляет собой умозаключение от общего к частному. В настоящей главе мы рассмотрим тот вид умозаключения, который называется индукцией, или наведением. Различие между этими двумя видами умозаключения сводится к следующему.

В дедуктивном умозаключении при признании какого-либо общего суждения мы необходимо должны признать какое-либо частное суждение или менее общее суждение; в индуктивном умозаключении мы от признания ряда частных суждений переходим к признанию общего суждения.

Определение индукции. Ближе индукцию можно определить следующим образом: индукция есть процесс мышления, посредством которого мы выводим, что истинное в каком-либо частном случае или частных случаях будет истинным и во всех случаях, сходных с предыдущими. Например, я заметил, что в нескольких случаях растения произрастали лучше от притока влаги; из этих наблюдений я делаю заключение, что это будет справедливо по отношению ко всем случаям произрастания известного класса растений. Если я наблюдаю, что какие-либо тяжёлые тела при погружении в воду теряют часть своего веса, равную весу вытесненной ими жидкости, то я делаю заключение, что это будет справедливо относительно всех тел и относительно всех жидкостей.

Таким образом, в процессе индуктивного умозаключения мы умозаключаем от случаев, которые мы наблюдали и исследовали, к случаям, которых мы не наблюдали и не исследовали. Далее, вследствие того, что в процессе индукции мы от наблюдения части класса умозаключаем ко всему классу, индукция есть умозаключение от частного к общему, или умозаключение от менее общего к более общему.

Не все, однако, считают это индукцией; некоторые философы думают, что индукцией следует называть такое умозаключение от частного к общему, в котором заключение относится ко всем исследованным случаям. Это та индукция, которая называется полной или совершенной.

Полная и неполная индукция. Полной индукцией называется тот вид индукции, в заключении которого говорится только о тех случаях, о которых говорится также и в посылках. Если я, рассмотрев месяцы года, нахожу, что ни один из них не имеет больше 31 дня, и высказываю это в виде общего положения, то это будет полной индукцией. Если я, исследовав национальность каждого ученика, сидящего в классе, и узнав, что каждый из них есть француз, выражаю в виде общего положения: «все ученики класса суть французы», то это будет полной индукцией. По мнению некоторых, это есть единственная индукция, заслуживающая названия индукции, потому, что она имеет безусловно достоверный характер. Но если принять то определение индукции, которое было предложено выше, то для нас сделается ясным, что такого рода заключения не могут быть названы индукцией, потому что индукция в собственном смысле есть умозаключение от известного к неизвестному. В индуктивном умозаключении в выводе всегда должно получаться что-нибудь новое, между тем как в полной индукции ничего нового не получается, потому что заключение в полной индукции есть только повторение в краткой форме того, что содержится в посылках: это есть простое резюмирование посылок. Индуктивным умозаключением является именно неполная индукция, которой мы из исследования только некоторых случаев умозаключаем к классу случаев; исследовав только часть класса, умозаключаем ко всему классу.

Популярная индукция. Существуют индуктивные построения, которые не могут удовлетворять требованиям научной точности. Это – построения, которыми склонно пользоваться популярное сознание и которые поэтому называются популярной индукцией.

В чём заключается популярная индукция?

Если мы имеем случаи наблюдать многократное повторение сходных явлений, то начинаем думать, что эти явления всегда будут иметь место, если только мы не имели случая наблюдать явлений, противоречащих им. Если мы, например, много раз во многих местах имели случай наблюдать, что лебеди имеют белый цвет перьев, то мы делаем заключение, что лебеди всегда и везде имеют белый цвет перьев. Такое заключение Бэкон назвал: inductio per enumerationem simplicem, ubi non reperitur instantia contradictoria (индукция через простое перечисление, в котором не встречается противоречащего случая), потому что в ней делается вывод на основании простого перечисления, пересмотра сходных случаев, которые были у нас в прошлом опыте и которым не было противоречащего случая. Кажется, что чем больше случаев наблюдаемой связи, тем большую достоверность приобретает выводимое заключение. Такая индукция не может быть признаваема достоверной, потому что то обстоятельство, что мы не встречали случаев, противоречащих тем, которые мы наблюдали, отнюдь не является ручательством, что всегда будет так, как мы наблюдали.

От популярной индукции отличается индукция научная. В этом процессе исследуют каждый отдельный наблюдаемый случай, анализируют его, всё случайное для данного явления отбрасывают, ищут существенные признаки его и строят заключения, приводя в связь и согласие эти последние с другими обобщениями. Такие выводы только и могут иметь характер более или менее достоверный. Это можно пояснить при помощи только что приведённого примера. Если мы на основании наблюдённых нами лебедей делаем заключение, что «все лебеди белы», то такая индукция будет популярной, потому что на основании тщательных исследований относительно цвета перьев птиц мы должны придти к заключению, что цвет представляет собой нечто непостоянное, не связанное необходимо с природой лебедя, а потому легко может случиться, что окажутся лебеди, обладающие чёрным цветом перьев.

Индукция должна иметь дело с необходимой связью вещей, а не со случайной. Связь между белым цветом перьев и организацией лебедя не является необходимой; чёрный цвет перьев лебедя не есть что-либо такое, что противоречит другим обобщениям. Цвет перьев для птиц не есть что-либо существенное, т.е. не есть что-либо такое, от чего могла бы зависеть жизнь или существо птиц. Совсем иное дело, если бы мы, произведя наблюдение над процессом дыхания у лебедей, сказали, что «лебеди дышат кислородом». Это было бы правильной научной индукцией, потому что способность вдыхания кислорода есть такое свойство, без которого птицы не мыслимы. Точно таким же образом мы поступаем во всех тех случаях, когда нам вообще приходится строить индуктивные положения относительно наблюдаемых нами явлений.

Понятия законов природы. Пользуясь индуктивным умозаключением, мы можем открывать законы природы.

Но что же такое законы природы?

Это – предложения, которые выражают постоянное свойство или постоянную связь каких-нибудь явлений. Например, положение, что «жидкость в сообщающихся сосудах находится на одном и том же уровне», есть закон природы. «Животные вдыхают кислород» – закон природы.

Первой существенной чертой закона природы следует признать его всеобщность: описание какого-нибудь единичного факта, хотя бы оно было совершенно верно, не может быть названо законом. Закон всегда служит для выражения свойств, общих ряду явлений или классу явлений.

Другая существенная черта в понятии закона – это необходимость. Положение «тело, лишённое опоры, будет падать» есть закон, потому что действительно тело, лишённое опоры, необходимо будет падать. «Железо теплопроводно» – закон природы, потому что в железе теплота будет необходимо распространяться, т.е. если теплота будет приведена в соприкосновение с железом, то это последнее необходимо будет проводить её. Если бы оказалось, что изучаемая связь один раз имеется налицо, а в другой раз не имеется, то мы то предложение, которое служит для выражения этой связи, не могли бы назвать законом. Вот почему научные обобщения, считающиеся законами, сейчас же перестают быть ими, как только найден хоть один случай, в котором они не применяются.

Основание индукции. Мы при помощи индукции исследуем природу, составляя общие положения. Но на чём мы основываемся, когда мы составляем такие общие положения? Что даёт нам право обобщать или на что мы опираемся, когда по одному факту или по ряду сходных фактов заключаем о классе сходных с ними фактов? Что даёт нам право делать выводы от наблюдённых случаев к не наблюдённым? Например, исследовав сжимаемость одного или двух газов, мы, обобщая, утверждаем, что «все газы сжимаемы». Для того чтобы мы имели право делать вывод от того, что мы наблюдали, к тому, чего мы не наблюдали, мы должны исходить из предположения, что вещи обладают постоянными свойствами, т.е., вещи устроены так, что сегодня известные причины вызывают те же действия, что и вчера, завтра известные причины будут вызывать те же действия, что и сегодня. Если соприкосновение железа с кислородом сегодня производит в нём ржавчину, то у нас есть уверенность, что так будет всегда, потому что железо и кислород обладают такими свойствами, что взаимодействие их всегда будет производить ржавчину. Таким образом, у нас есть убеждение, что вещи, будучи поставлены в определённые условия, обладают постоянными свойствами и поэтому во всех случаях действуют единообразно. Это можно ещё иначе выразить, если сказать, что в природе существует определённый порядок. Только благодаря тому, что у нас есть такое убеждение, мы можем умозаключать от вещей наблюдённых к вещам не наблюдённым.

Вопросы для повторения

Как определяется индукция? Чем отличается индукция от дедукции? Что такое полная и неполная индукция? Что такое популярная индукция и чем она отличается от научной? На чём основан вывод в популярной индукции? Что такое законы природы и каковы их характерные особенности? На каком законе основывается индукция?

Источник

3. Неполная индукция

3. Неполная индукция

Неполной индукцией называется умозаключение обо всем классе предметов в целом на основе изучения лишь части предметов данного класса.

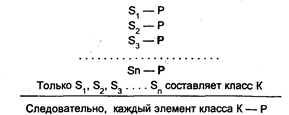
Формула неполной индукции:

Следовательно, все S — Р.

В символической записи:

Посредством неполной индукции преодолевается недостаток полной индукции. Она применяется прежде всего там, где число элементов исследуемого класса неопределенно, неограниченно или бесконечно. Таковы так называемые «открытые классы». Правда, она может применяться и там, где это число ограниченно и его нетрудно сосчитать («закрытые классы»), однако надобности в исследованиях всех без исключения элементов почему-либо нет. Так была установлена, например, электропроводность металлов на основе знания лишь о некоторых металлах, хотя число их определенно.

Возможность заключения в форме неполной индукции обусловлена тем, что если некоторое общее свойство принадлежит более или менее значительной части класса, то в силу его большей или меньшей существенности оно может принадлежать и всему классу в целом.

Познавательное значение неполной индукции по сравнению с полной в известном смысле более важно и велико. Как отмечалось, в полной индукции заключение не распространяется на другие предметы, кроме изученных, хотя весь их класс в целом и рассматривается с новой стороны. В заключении же неполной индукции осуществляется логический перенос знания с изученной части класса на всю остальную его часть.

Однако в этом достоинстве неполной индукции содержится и ее существенный недостаток. В отличие от полной индукции сам вывод здесь — даже при истинности всех посылок — может давать в принципе лишь вероятное знание, способное в большей или меньшей степени приближаться к достоверному. Обобщение, содержащееся в нем, может обеспечивать и твердое, достоверное знание, но лишь в том случае, если оно облекается в форму частного суждения. Однако кванторное слово — по сравнению с полной индукцией — употребляется здесь в ином смысле: «Некоторые, а может быть и все». Следовательно, сами такие обобщения носят характер неопределенного частного суждения.

Неполная индукция имеет две основные разновидности: это популярная индукция и научная индукция.

Популярная индукция (или индукция через простое перечисление). Ее полное наименование: «индукция через простое перечисление, когда не встречается противоречащий случай» («inductio per enumerationem simplicem, ubi non reperitur instantia contradictoria»). Повседневная жизнь людей дает массу примеров такой индукции. Так, люди не раз наблюдали, что ласточки перед дождем летают низко над землей. На этой основе был сделан вывод: «Всегда ласточки перед дождем летают низко над землей». Подобных примет, сделанных на основе непосредственных наблюдений, зафиксировано народной мудростью немало. Вот почему они получили название «народные приметы», а сама индукция — наименование «популярная» («народная»). Однако такие выводы носят характер лишь вероятного знания. Достаточно встретиться противоречащему случаю, чтобы заключение оказалось ложным. Вспомним классическую историю с лебедями. На основе бесчисленных наблюдений издавна был сделан вывод, что «Все лебеди белы». Однако со временем в Австралии были обнаружены черные лебеди, которых теперь можно видеть и в других местах. То же самое с выводом: «Все березы белы». Оказывается, есть и черные березы. С подобной проблемой столкнулась знаменитая «курица Рассела». У Б. Рассела есть такая притча. В курятнике живет курица. Ежедневно приходит хозяин, приносит ей поклевать зернышек. Курица, естественно, делает отсюда вывод: с появлением хозяина связано появление зернышек. Но вот однажды хозяин является не с зернышком, а с ножом. Это и есть «противоречащий случай»!

Степень вероятности получения истинного вывода на основе популярной индукции зависит от двух важнейших условий: 1) количества обозреваемых случаев; 2) качества признака, т. е. степени его существенности для данного класса предметов.

Однако и это не в состоянии устранить основные недостатки популярной индукции. Один из них состоит в том, что дается простое перечисление случаев повторяемости одного и того же признака и не делается сознательного отбора типичных фактов и их специального анализа. Другой — в том, что обобщение производится на основе простого наблюдения случайно попавшейся совокупности предметов класса и не исследуется причина самого явления. Вот почему наряду со многими верными народными приметами есть немало ложных обобщений, лежащих в основе суеверия, поверий, заклинаний и т. п., — о «пустых ведрах», «черной кошке», «сглазе», «заговоре» и пр.

Научная индукция. Отмеченные выше недостатки популярной индукции преодолеваются так называемой «научной индукцией» (хотя правильно называть ее неполной научной индукцией, так как научной может быть и полная). С ее помощью не просто наблюдаются отдельные случаи, а исследуется природа самого явления и дается ответ на вопрос: «Почему так, а не иначе?» Например, достаточно понять, что ласточки перед дождем летают низко над землей потому, что низко летают мошки, за которыми они охотятся; а те летают низко потому, что перед дождем у них набухают крылышки. Благодаря этому степень вероятности получения истинного вывода в неполной индукции значительно повышается.

Другой пример. В результате популярной индукции было установлено, что металлы при нагревании расширяются. Но все или только некоторые? И лишь молекулярная теория, раскрыв механизм этого расширения, сделала общий вывод, и притом вывод достоверный.

Если в популярной индукции важно обозреть как можно большее число случаев, то для научной индукции это не имеет принципиального значения. Легенда гласит, что Ньютону для открытия фундаментального закона всемирного тяготения достаточно было наблюдать один случай — падение яблока. Это легенда. Но вот факт. Известно, что исходным пунктом для открытия Р. Майером другого фундаментального закона — закона сохранения и превращения энергии послужили наблюдения над цветом крови людей в разных климатических поясах. Открытие многих законов в естественных и общественных науках так или иначе связано с индукцией, зачастую неполной.

Конечно, в разных науках неполная индукция проявляется по-разному. Так, в познании микромира, где действуют преимущественно статистические закономерности, широко используется статистическая индукция. Она нередко применяется в социологических исследованиях: например, при выявлении рейтинга того или иного политического деятеля, вероятности избрания того или иного человека на какой-либо государственный пост и при других опросах общественного мнения. Однако в любой разновидности научной индукции действуют общие закономерности, исследуемые формальной логикой.

Читайте также

3.13. Что такое индукция?

3.13. Что такое индукция? Вспомним, опосредованные умозаключения делятся на дедуктивные, индуктивные и умозаключения по аналогии. Дедуктивные умозаключения, или силлогизмы, разновидности которых мы рассмотрели выше, дают достоверные выводы. Индуктивное умозаключение,

§ 2. ПОПУЛЯРНАЯ ИНДУКЦИЯ

§ 2. ПОПУЛЯРНАЯ ИНДУКЦИЯ В процессе многовековой деятельности люди наблюдали устойчивую повторяемость многих явлений, которые обобщались и использовались в объяснении наступивших и предсказании будущих событий.Такого рода обобщения связаны с наблюдениями над погодой,

§ 3. НАУЧНАЯ ИНДУКЦИЯ

§ 3. НАУЧНАЯ ИНДУКЦИЯ Научной индукцией называют умозаключение, в котором обобщение строится путем отбора необходимых и исключения случайных обстоятельств.В зависимости от способов исследования различают: (1) индукцию методом отбора (селекции) и (2) индукцию методом

Глава V. Индукция

Глава V. Индукция Другой, кроме дедукции, наиболее общий тип умозаключений — это индукция. В ней заключено глубокое своеобразие, и она находится в тесных взаимоотношениях с дедукцией. В реальной практике мышления ее сущность проявляется тоже в многообразных

2. Полная индукция

2. Полная индукция Полной индукция получается в том случае, если, во-первых, исследованы все элементы класса предметов и, во-вторых, если установлено, что каждому из них принадлежит (или не принадлежит) одно и то же общее свойство (отношение).В простейшем случае это выглядит

Глава V. Индукция

Глава V. Индукция 1. Индукция как тип умозаключения Выразите структуру следующих индуктивных умозаключений в схематической форме и определите характер вывода: «Возьмем, например, исследование Роджера Бэкона о происхождении цветов радуги. Сначала у него, как кажется,

1. Индукция как тип умозаключения

1. Индукция как тип умозаключения Выразите структуру следующих индуктивных умозаключений в схематической форме и определите характер вывода: «Возьмем, например, исследование Роджера Бэкона о происхождении цветов радуги. Сначала у него, как кажется, была мысль связать

§ 6. Математическая индукция

§ 6. Математическая индукция «Но не забываете ли вы, что в математике также имеет место индукция?» – может возразить читатель. «Вы описывали математику как типичную дедуктивную науку, в которой все теоремы являются необходимыми следствиями аксиом. Однако вы ведь не

НЕПОЛНАЯ ИНДУКЦИЯ

НЕПОЛНАЯ ИНДУКЦИЯ Индуктивное умозаключение, результатом которого является общий вывод обо всем классе предметов на основании знания лишь некоторых предметов данного класса, принято называть неполной или популярной индукцией. Например, из того, что инертные газы

Полная и неполная индукция

Полная и неполная индукция Если мы переберём всех футболистов сборной России и выясним, что среди них нет одноногих — это будет полная индукция, она же — «индукция перебором».Если же мы изучим одного футболиста, и придём к выводу, что играть с протезом в сборной —

Популярная индукция

Популярная индукция Популярная, она же народная индукция — это индукция через перечисление. Та самая, про которую мы говорили вчера. «Если три моих знакомых еврея хитры, то и все евреи хитры».Популярная индукция — одно из любимых орудий демагогов. Например: Василий

Научная индукция

Научная индукция Научная индукция работает иначе. Научная индукция объясняет свои выводы. Вернёмся к нашему примеру с хитрыми евреями. Научная индукция для этого примера может выглядеть так:«Мозг этих трёх евреев имеет особый отдел мозга, отвечающий за хитрость, и этот

Индукция по простому перечислению

Индукция по простому перечислению Раньше эту ошибку даже разбирали в школах. Примерно так: Учительница: Как полагаете дети, негры глупее белых? Вовочка: Конечно, Марь Иванна! Мы же не знаем ни одного великого негра-учёного или негра-писателя! Учительница: Вовочка, ты

Индукция (Induction)

Индукция (Induction) Вид доказательства, в классическом понимании определяемый как переход от частного к общему, или от фактов к закону. Тем самым противостоит дедукции, которая обычно идет от общего к частному, от принципа к следствиям.Нетрудно догадаться, что индукция,

Источник