Что такое неполное частное при делении с остатком

ВОПРОСЫ

1. Каким свойством обладает неполное частное при делении с остатком?

2. Сравните остаток и делитель.

Остаток всегда меньше делителя.

3. Сформулируйте правило нахождения делимого при делении с остатком.

Правило нахождения делимого при делении с остатком: чтобы найти делимое, надо делитель умножить на неполное частное и прибавить остаток.

4. Как записывают в буквенном виде правило нахождения делимого?

5. В каких случаях говорят, что одно натуральное число делится нацело на другое?

Говорят, что одно натуральное число делится нацело на другое, если при делении первого числа на второе остаток равен нулю.

РЕШАЕМ УСТНО

1. Найдите числа, которых не хватает в цепочке вычислений:

2. В числе 72 560 000 зачеркнули три последних нуля. Как изменилось, увеличилось или уменьшилось, это число и во сколько раз?

Число уменьшилось в 1000 раз.

4. Уменьшаемое на 129 больше вычитаемого. Чему равна разность?

Разность данных чисел равна 129.

5. Делитель в 48 раз меньше делимого. Чему равно частное?

Частное данных чисел равно 48.

УПРАЖНЕНИЯ

521. Выполните деление с остатком:

522. Выполните деление с остатком:

523. 1) Найдите остаток при делении на 10 числа: 31; 47; 53; 148; 1 596; 67 389; 240 750.
2) Найдите остаток при делении на 5 числа: 14; 61; 86; 235; 2 658; 54 769; 687 903.

524. Найдите остаток при делении на 100 числа: 106; 202; 421; 836; 2 764; 100 098; 672 305; 1 306 579; 562 400.

525. Запишите остатки, которые можно получить при делении на: 1) 7; 2) 13; 3) 24.

526. Запишите остатки, которые можно получить при делении на: 1) 5; 2) 19.

527. Блокнот стоит 26 р. Сколько блокнотов можно купить на 140 р.?

528. Один грузовик можно нагрузить 5 т песка. Сколько требуется таких грузовиков, чтобы перевезти 42 т песка?

529. В один ящик помещается 20 кг яблок. Сколько надо ящиков, чтобы разложить в них 176 кг яблок?

530. Заполните таблицу.

536. При каком наименьшем натуральном а значение выражения:
1) 53 + а делится нацело на 7;
2) а + 24 при делении на 5 дает остаток 2?

537. Катя разделила число 211 на некоторое число и получила в остатке 26. На какое число делила Катя?

538. Миша разделил число 111 на некоторое число и получил в остатке 7. На какое число делил Миша?

539. Павел разделил число 70 на некоторое число и получил в остатке 4. На какое число делил Павел?

540. Какое наибольшее количество понедельников может быть в году?

541. В одном осеннем месяце суббот и понедельников оказалось больше, чем пятниц. Каким днем недели было девятнадцатое число этого месяца? Какой это был месяц?

545. Упростите выражение и найдите его значение:

546. Периметр прямоугольника равен 54 см, а его ширина на 3 см меньше длины. Найдите стороны прямоугольника.

ЗАДАЧА ОТ МУДРОЙ СОВЫ

547. Известно, что веревка сгорает за 4 мин и горит при этом неравномерно. Как с помощью: 1) одной веревки отмерить 2 мин; 2) двух таких веревок отмерить 3 мин?

Источник

Общее представление о делении натуральных чисел с остатком

В данном материале мы разберем, как разделить одно натуральное число на другое с остатком. Для начала сформируем общее представление о таком действии, определимся с терминами и обозначениями, а потом посмотрим, какие задачи можно решить с его помощью. В последнем пункте попробуем объяснить, какие связи существуют между понятиями делимого, делителя, неполного частного и остатка от деления.

Общее представление о делении с остатком

Разделить с остатком – значит представить исходное множество в виде некоторого числа равных множеств и еще одного дополнительного, элементов которого недостаточно для создания требуемого множества.

В чем состоит смысл деления с остатком?

1) если b –количество элементов в каждом равном множестве, полученном после деления, то c – это количество множеств, которое у нас получилось.

2) если b – это количество множеств, то c – это число предметов в каждом из них.

Основные понятия, используемые при делении с остатком

Здесь мы определимся с основными терминами, которые будем использовать, если речь идет о делении с остатком.

Знак деления, используемый при решении примеров с остатком, аналогичен тому же знаку «разделить» (две точки, расположенные вертикально), что и при делении нацело. В некоторых источниках можно встретить обозначение « ÷ », смысл которого тот же самый. Так, числовое выражение 16 : 3 означает деление одного натурального числа на другое с остатком.

Также можно записать это в виде схемы: делимое: делитель = неполное частное (ост. остаток).

Из самого понятия о делении с остатком следует, что в любом случае остаток будет меньше делителя. Если бы он был равен ему или был нулевым, то это уже было бы деление нацело, поскольку у нас в итоге вышло бы несколько равных множеств.

Задачи, в которых используется деление с остатком

В результате процесса деления, описываемого в этой статье, всегда получаются два числа, одно из которых является остатком, а другое – неполным частным. Поэтому оно будет полезно для решения двух разных типов задач:

1. Нахождение количества необходимых равных множеств, которые можно составить из заданного количества предметов, или же количества предметов в равных множествах, полученных в результате деления.

У нас есть 67 шаров, которыми мы будем наряжать елки. Если на каждую елку нужно 15 шаров, сколько всего елок можно нарядить? Результат мы получим после деления с остатком.

Вычислять мы можем не только количество предметов, но и изменения величин (массы, времени, длины и др.)

Например, на заводе произведено 6 113 л молока. Его нужно разлить в бутылки по 2 л. Мы можем вычислить неполное частное и понять, сколько бутылок будет в итоге. Или же если на производство какого-то изделия тратится 3 часа, то мы можем найти, сколько можно их выпустить за один восьмичасовой рабочий день.

2. Задачи второго типа направлены на вычисление количества предметов в исходном множестве, которые остались после деления. Это могут быть не только предметы, но и величины.

Чтобы изготовить бетонную плиту, надо израсходовать 750 кг цемента. Если мы закупили 12 900 кг, на сколько плит нам хватит? Результат мы вычислим в результате деления с остатком.

Основные связи между понятиями делимого, делителя, неполного частного и остатка от деления

Для установления этих связей сразу разберем конкретный пример.

Если у нас есть значения делителя, неполного частного и остатка, мы можем найти делимое. Если мы объединим все имеющиеся кучки и добавим к ним остаток, то получим множество из исходного количества предметов.

Чтобы найти делимое, нужно сложить остаток с произведением делителя на неполное частное.

Верное равенство, полученное в итоге, будет полезно для решения задач с неизвестным делимым, то есть таких, где нужно найти исходное число предметов. Приведем пример:

Вычислите делимое, если неполное частное равно одиннадцати, остаток двум, а делитель семи.

Решение

Если нам известны значения делимого, делителя и неполного частного, то мы можем найти остаток.

Чтобы найти остаток от деления одного натурального числа на другое, нужно вычесть из делимого произведение делителя на неполное частное.

Решение

Если нужно найти неполное частное, нужно из делимого вычесть остаток и результат разделить на делитель.

Решение

Отнимем остаток от делимого и результат разделим на делитель. Считаем: ( 221 − 13 ) : 52 = 208 : 52 = 4 (для подсчета мы использовали метод подбора частного).

Найти делитель можно, если вычесть из делимого остаток и получившуюся разность разделить на неполное частное.

Возьмем пример решения такой задачи.

Решение

Источник

Деление натуральных чисел

Подобно тому, как вычитание является обратным действием для сложения, так и для умножения существует свое обратное арифметическое действие.

Рассмотрим задачу. В школьной столовой раздали 90 яблок по 3 яблока каждому ученику класса. Сколько учеников учатся в этом классе?

Если бы нам было известно количество учеников в классе и количество яблок, которое получил каждый из них, то общее число яблок мы узнали бы, умножив число учеников на число яблок, доставшееся каждому. То есть, количество учеников – это первый сомножитель, количество яблок – второй сомножитель, а сколько яблок раздали – это произведение.

Деление – это арифметическое действие, которое состоит в нахождении одного из сомножителей при помощи данного произведения и второго сомножителя.

Делимое – это число, которое мы делим на другое. Это то самое произведение, которое нам дано.

Делитель – это число, на которое мы делим делимое. Это данный нам один из множителей.

Частное – это результат действия деление, то есть, искомый нами второй сомножитель.

На записи действие деление обозначается: двоеточием ( \(\textcolor <:>\) ), знаком обелюс ( \(\textcolor <\div>\) ), горизонтальной чертой или косой чертой ( \(\textcolor \) ).

Так, решение нашей задачи можно записать следующими способами:

При записи от руки действие деление принято записывать в виде двоеточия, обелюс применяется в печатной литературе, косая черта, которая по-другому называется слеш, – при записи на компьютере, а горизонтальная черта используется при записи деления в виде обыкновенной дроби.

Итак, разделить число a на число b – это значит найти такое число c, которое при умножении его на число b дает в результате числа a.
То есть: \(\textcolor \) , если \(\textcolor \) .

Компоненты действия деление:

Деление с остатком и неполное частное

К примеру, если мы захотим раздать все 37 яблок поровну между пятью детьми, то у нас это сделать не получится. Мы сможем раздать (использовать из всего количества яблок) только по 7 яблок каждому ( \(\textcolor <7\cdot 5=35>\) ), и у нас останется 2 яблока ( \(\textcolor <37-35=2>\) ).

Итак, деление с остатком – это нахождение такого наибольшего целого числа, умножив которое на делитель, мы получим число, максимально близкое к делимому, но не превосходящее его. Это искомое число называется неполное частное. Разница между делимым и неполным частным называется остаток.

Остаток всегда меньше делителя!

Связь деления с умножением, сложением и вычитанием

Когда мы выполняем находим произведение двух чисел, эти числа нам известны, а от нас требуется найти результат действия умножение. При делении (без остатка) нам известно произведение двух чисел, а найти нужно такое число, которое при умножении на известное данное число дает это самое произведение.

Следовательно, действие деление является обратным действию умножения.

Справедливо также и обратное, что действие умножение обратно действию деления. Таким образом:

Умножение и деление – это взаимно обратные действия.

Связь деления с умножением, а также со сложением и вычитанием прекрасно видна, если рассмотреть, как с помощью этих действий можно выполнить действие деление.

Деление двух чисел при помощи сложения

Деление двух чисел при помощи вычитания

То есть, 69 от 345 можно отнять 5 раз, поэтому \(\textcolor <349\div 69=5>\).

Деление двух чисел при помощи умножения

При помощи умножения узнать ответ на наш вопрос можно перебирая множитель числа 69 до тех пор, пока не получим заданное нам 345 :

Но эти три способа очень громоздки, особенно если частное представляет собой очень большое число. Их нужно знать только для того, чтобы понимать суть действия деления, суть тех задач, которые решаются посредством него.

Общий принцип деления в столбик

Если частное от деления двух чисел является многозначным числом, нахождение его происходит путем деления в столбик. Еще его называют деление уголком.

Прежде всего, нужно узнать количество цифр в частном и первое неполное делимое; как их находить, я подробно расписал в этой статье. В нашем случае первое неполное делимое равно 295 тысяч, а в частном будет 4 цифры.

Далее записываем известные компоненты деления следующим образом:

и начинаем вычисление:

1. Берем первое неполное делимое и пытаемся его разделить на делитель.

Вот тут нам и пригодится способ нахождения однозначного частного. Воспользовавшись им, находим, что в 295 тысячах делитель 34 содержится целиком 8 тысяч раз.

Записываем в частное первую найденную цифру разряда тысяч, а под неполным делимым пишем результат произведения неполного частного и делителя. И сразу же находим остаток от этого действия, т.е. вычитаем из неполного частного результат этого произведения.

В результате умножения первой найденной цифры частного на делитель у нас получилось \(\textcolor <8\cdot 37=272>\). Записываем его под 295 и находим разницу: \(\textcolor <295-272=23>\). Значит, 23 тысячи у нас остаются неразделенными.

В качестве еще одного действия самопроверки нужно сравнить полученную разницу с делителем. Если она меньше делителя, то мы на правильном пути, если же разница равна или больше делителя, то мы или неправильно нашли цифру частного, или допустили ошибку при умножении на делитель либо при нахождении остатка.

2. Оставшиеся неразделенные 23 тысячи представляют собой 230 сотен. Прибавляем к ним те 3 сотни, которые содержатся в делимом (говорят: сносим пять) и получаем второе неполное делимое 233 сотни.

3. 29 неразделенных сотен – это 290 десятков. Добавляем (сносим) к ним 8 десятков делимого, получаем третье неполное делимое 298 десятков.

4. И наконец, 26 десятков – это 260 простых единиц. Добавляем (сносим) к ним 3 единицы делимого и получаем четвертое неполное делимое 263 единицы.

Рассмотрим еще один пример. \(\textcolor <25326\div 63>\).

1 сотня = 10 десятков, добавляем (сносим) 2 десятка из делимого, получаем второе неполное делимое 12 десятков.

Итак, запомните, что каждое неполное делимое образует в частном одну цифру соответствующего разряда и что даже если неполное делимое меньше делителя, то в частном все равно нужно записать нулевой результат этого действия.

Итак, в общем виде алгоритм деления в столбик выглядит так:
1. Находим первое неполное делимое и количество цифр в частном.
2. Делим неполное делимое на делитель. Цифру, полученную в результате деления записываем ниже черты под делителем.
3. Умножаем полученную цифру на делитель, результат записываем под неполным делимым.
4. Ставим между ними знак минус и выполняем действие.
5. К полученной разнице сносим цифру следующего разряда (если она есть) и получаем второе неполное делимое.
6. Выполняем пункты 2-5 до тех пор, пока в делимом не останется ни одной неснесенной цифры.
7. Если неполное делимое невозможно разделить на делитель, то в частном ставится 0 и к этому неполному делимому сносится следующая цифра.

Деление на числа, заканчивающиеся нулями

Как и в случае с умножением, деление чисел облегчается, если делитель заканчивается одним или несколькими нулями. Рассмотрим два возможных случая:

Рассмотрим первый случай.

Деление на единицу с любым количеством нулей

Единица с любым количеством нулей – это не что иное как единица соответствующего разряда. Например, 10 – это 1 единица разряда десятков, 1000 – это одна единица разряда тысяч, 10000000 – 1 единица разряда десятков миллионов и т.д.

Запишите:
Чтобы разделить какое-нибудь число на единицу с любым количеством нулей, нужно отсчитать в делимом справа столько цифр, сколько нулей содержится в делителе; тогда все цифры, находящиеся слева от разделения, составят частное, а те, что справа – будут остатком.

Деление на число, оканчивающееся нулями

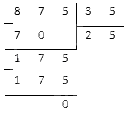
Рассмотрим на примере \(\textcolor <284556\div 2800>\).

Делитель здесь не что иное как 28 сотен. Логично предположить, что эти 28 сотен могут хотя бы один раз содержаться только в сотнях делимого. Значит, нам нужно определить, сколько в делимом всего единиц разряда сотен, и разделить их на 28 единиц разряда сотен делимого. А отброшенные цифры десятков и простых единиц добавятся к остатку.

Запишите:
Чтобы разделить какое-нибудь число на число, заканчивающееся нулями, нужно отбросить мысленно нули в делителе, в делимом тоже отбросить мысленно такое же количество цифр, как и нулей в делителе. Получившееся число в делимом разделить на получившееся число в делителе, а к остатку прибавить (снести) те цифры делимого, которые отбросили ранее.

Проверка деления

Так как делимое – это делитель, умноженный на частное и плюс остаток, что следует из определения деления, то результат выполнения деления можно проверить умножением.

Если в результате действия деления не получилось остатка, то деление можно проверить и делением. Действительно, если делимое – это произведение делителя и частного, то разделив делимое на частное (один из сомножителей), мы должны получить второй сомножитель, то есть, делитель.

Свойства деления

Свойства деления я представлю двумя группами:

Давайте рассмотрим каждую группу подробнее.

Действия деления с единицей и нулем

При делении числа на единицу получается то же самое число.

Действительно, разделить число на единицу означает узнать, сколько единиц содержится в данном числе. А количество единиц в числе – это не что иное, как само это число.

И ли вот, например, если 10 яблок нужно раздать одному человеку ( 10 поделить на 1 ), то ему все эти 10 яблок и достанутся, правда?

При деление одинаковых чисел (числа на равное число) в результате будет 1 (единица).

В самом деле, если все единицы какого-то числа разделить на количество частей, равное количеству единиц этого числа, то в каждая часть получит по 1 единице.

Например, если 20 яблок раздать 20 школьникам, то каждому достанется по 1 яблоку.

При делении нуля на любое число, отличное от нуля, в результате будет нуль.

Разделить нуль на число означает найти такое число, умножив которое на данный делитель, мы получим в результате нуль. А такое число только одно – это нуль.

На нуль делить нельзя, то есть, нуль не может выступать в роли делителя.

При делении каких угодно чисел делителем может быть любое число, кроме нуля.

Рассмотрим два случая: когда нулём является только делитель, и когда делимое и делитель оба нули.

Распределительные свойства деления

Чтобы найти частное от деления суммы на число, нужно поделить каждое слагаемое на это число, и найти сумму полученных частных.
\(\textcolor <(a+b+c)\div d=a\div d+b\div d+c\div d>\).
При этом подразумевается, что все действия деления получаются без остатка.

Чтобы найти частное от деления разности на число, нужно поделить на это число отдельно сперва уменьшаемое, а потом вычитаемое, после чего найти разность первого частного и второго.
\(\textcolor <(a-b)\div c=a\div c-b\div c>\)
При этом также предполагается, что при делениях уменьшаемого и вычитаемого на число не получается остатков.

Например: \[\textcolor <(36-24)\div 6=36\div 6-24\div 6=6-4=2>\] Число 36 состоит из 6 шестерок, а 24 – из 4 шестерок, а забрав у 6 шестерок 4 шестерки, получим 2 шестерки. Такой же итог будет и если мы сперва у 36 отнимем 24 единицы (останется 12 ), а потом найдем, сколько в этой разнице содержится шестерок: \(\textcolor <12\div 6=2>\).

Чтобы найти частное от деления произведения на число, нужно поделить на него только один из сомножителей, а результат умножить на неизмененные остальные.
\(\textcolor <(a\cdot b\cdot c)\div d=a\div d\cdot b\cdot c=b\div d\cdot a\cdot c=c\div d\cdot a\cdot b>\).

Чтобы найти частное от деления числа на произведение, нужно это число поделить на первый сомножитель, результат деления поделить на второй сомножитель, полученное частное – на третий и так далее.
\(\textcolor \).
При этом предполагается, что при всех этих делениях не получается остатков.

На рисунке наглядно видно, что в итоге после применения этого правила, число 30 получилось разделенным на 6 равных частей.

Изменение частного при изменении делимого и делителя

При рассмотрении изменений частного в результате изменений делимого и делителя предполагается, что действие деление происходит без остатка. В противном случае изменения могут быть не такими, о которых идет речь ниже.

При увеличении делимого в определенное количество раз, частное увеличится в это же количество раз, а при уменьшении – уменьшится.

Если мы в примере \(\textcolor <24\div 4=6>\) делимое увеличим, к примеру, в 3 раза, то мы можем переписать это выражение в виде \(\textcolor <(24+24+24)\div 4>\). Используя свойство деления суммы на число, мы увидим, что теперь нам нужно сложить три слагаемых, каждое из которых равно начальному выражению: \(\textcolor <24\div 4+24\div 4+24\div4>\). Отсюда очевидно, что результат будет больше начального в 3 раза.

Если мы в этом же примере \(\textcolor <24\div 6>\) уменьшим делимое в 3 раза, то есть, разделим его на три равные части, то очевидно, что результат деления одной части на 6 будет в 3 раза меньше, чем результат деления трех таких же частей. Посмотрите сами. Начальное выражение \(\textcolor <24\div 6>\) можно записать в виде: \(\textcolor <(8+8+8)\div 6=8\div 6+8\div 6+8\div 6>\), а уменьшенное в 3 раза делимое даст нам только одно из трех таких слагаемых: \(\textcolor <8\div 6>\).

При увеличении делителя в определенное количество раз, частное уменьшится в это же количество раз, а при уменьшении – увеличится.

Действительно, изменение делителя означает, что делимое необходимо разделить на большее или меньшее количество равных частей. Соответственно, если нужно разделить на большее число частей, то каждая часть будет меньше, чем изначально, а если делить на меньшее число частей, то каждая часть будет крупнее.

В случае одновременного изменения делимого и делителя, частное может вести себя по-разному, или же вообще оставаться без изменений. Если нужно узнать, станет оно больше или меньше, нужно сперва посмотреть, как частное изменится после изменения делимого, а потом – как изменится после изменения делителя.

При увеличении или уменьшении делимого и делителя в одинаковое количество раз, частное не меняется.

Попробуйте самостоятельно доказать справедливость этого утверждения. Пишите в комментариях, получилось это, или нет.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 3.7 / 5. Количество оценок: 3

Источник