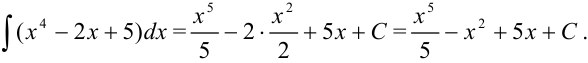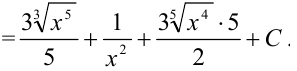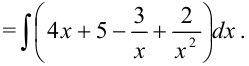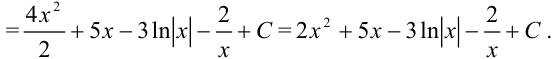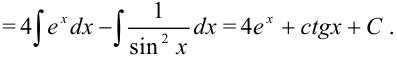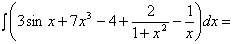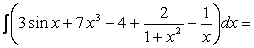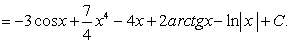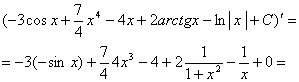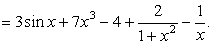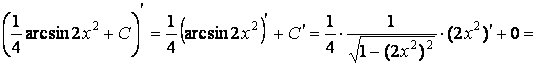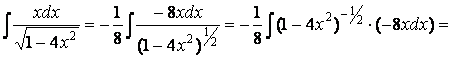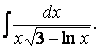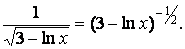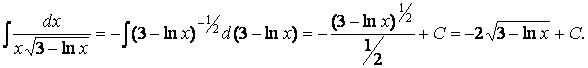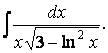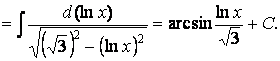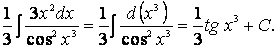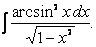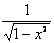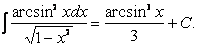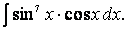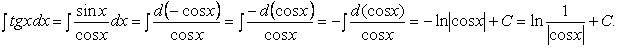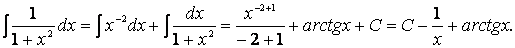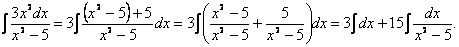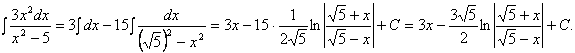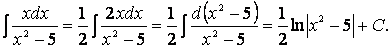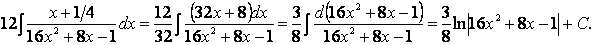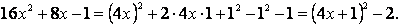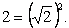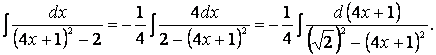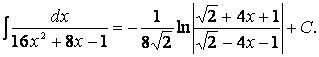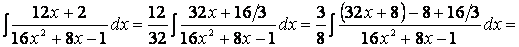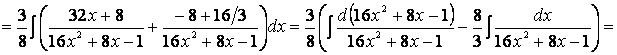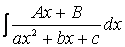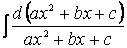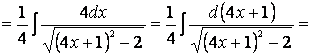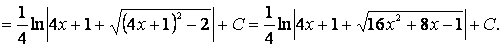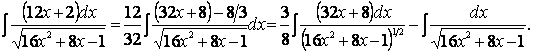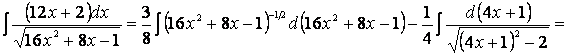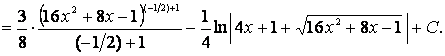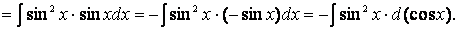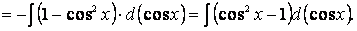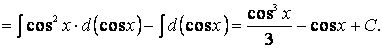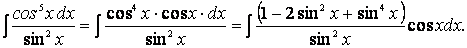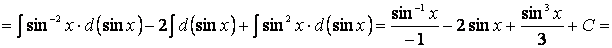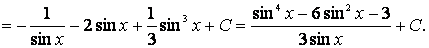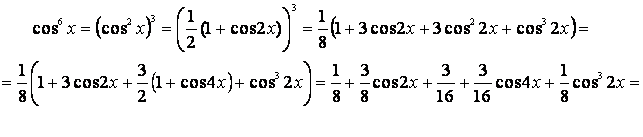Что такое непосредственное интегрирование
Непосредственное интегрирование
Под непосредственным интегрированием понимают такой способ интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам.
Пример №19.1.
Найдите 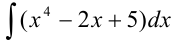
Решение:
Воспользуемся свойствами неопределенного интеграла: представим интеграл как сумму и разность соответствующих интегралов:
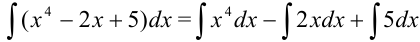
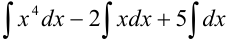
Пример №19.2.
Найдите 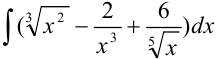
Решение:
Каждое слагаемое, стоящее под знаком интеграла, представим в виде степени с рациональным показателем. Для этого применим следующие свойства степени: 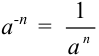
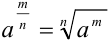
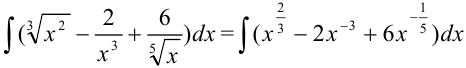
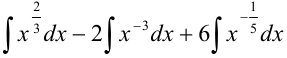
интегралом 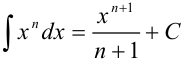
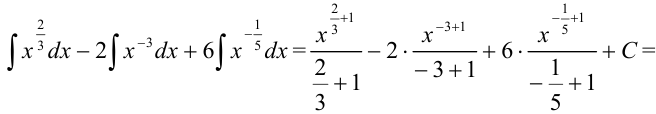
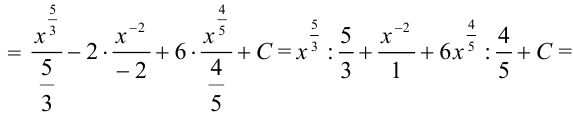
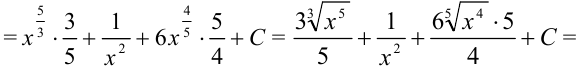
Пример №19.3.
Найдите 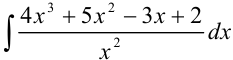
Решение:
Разделив почленно числитель на знаменатель, получим
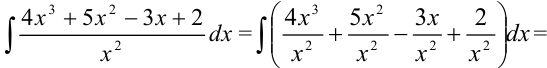
Представим данный интеграл как сумму и разность интегралов, вынесем константы за скобки:
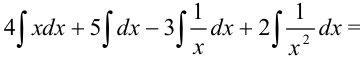
Пример №19.4.
Найти 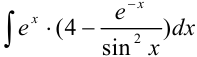
Решение:
Раскрывая скобки и применяя табличные интегралы, получим:
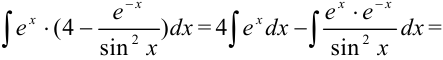
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
1.1. Способ непосредственного интегрирования
Предварительно изучите по учебнику Г. М. Фихтенгольца «Основы математического анализа», т. I, главу X, п° 155—159. Обратите особое внимание на примеры, решенные в п° 159.
Способ непосредственного интегрирования опирается на таблицу основных интегралов и простейшие правила интегрирования.
Таблица I. Таблица основных интегралов
Все эти формулы справедливы независимо от того, является ли и независимой переменной, либо какой угодно функцией этой независимой переменной. По поводу формул 5), 6), 9), 11) и 12) смотрите учебник п° 159.
Простейшие правила интегрирования (здесь cl?*— постоянная величина,
Очень часто встречаются случаи, когда с= I либо 6=0.
При отыскании неопределенных интегралов полезно помнить таблицу дифференциалов, но не в том виде, как она дана в учебнике (см. п° 91), а в немного преобразованном следующем виде (здесь как бы правые и левые части поменялись местами).
Таблица 2. Таблица дифференциалов
Этой таблицей мы в дальнейшем будем широко пользоваться. При этом представление, например, выражения
в виде Или выражения В виде Мы будем называть подведением функций соответ ственно Или Под знак дифференциала.
Решение. Записываем подынтегральную функцию в виде степени с отрицательным дробным показателем и применяем формулу I из таблицы I:
Решение. Числитель подынтегральной функции делим почленно на знаменатель. Затем применяем правила
II, I и формулу I из таблицы I:
Решение. Возводим числитель в квадрат и делим почленно на знаменатель. Далее поступаем, как в задаче 2:
Решение. Сначала исключаем целую часть рациональной дроби, деля числитель на знаменатель. Имеем:
Применяя теперь правило II, получим:
Первые два интеграла правой части (I) вычисляются по формуле I из таблицы I:
К третьему же интегралу правой части применяем правило III интегрирования. В нашем случае Поэтому на основании формулы 2 из таблицы I имеем:
Укажем другой способ рассуждений при вычислении третьего интеграла в правой части равенства (I).
*) Произвольную постоянную мы учтем позднее при написании окончательного ответа. Мы будем поступать так и в дальнейшем.
Интеграл не изменился, так как мы подынтегральное выражение помножили на 2 и одновременно интеграл разделили на 2. Если мы теперь множитель 2 при dx подведем под знак дифференциала (см. формулу I из табл. 2), то получим:
где и = 2х—I. Мы получили табличный интеграл (см. формулу 2 из табл. I).
Замечание. Если подынтегральная функция представляет собой рациональную дробь, у которой степень многочлена числителя больше или равна степени многочлена знаменателя, то прежде всего следует исключить целую часть путем деления числителя рациональной дроби на знаменатель.
Решение. Освобождаемся от иррациональности в знаменателе:
Мы воспользовались здесь правилом III и формулой I из таблицы I.
Мы использовали здесь правило II; подведением соответствующего постоянного множителя под знак дифференциала мы привели интегралы к табличным (см. формулы 6 и 7 из табл. I).
Решение. Чтобы свести данный интеграл к табличному (см. формулу 9 из табл. I), достаточно подвести под дифференциал множитель И разделить весь интеграл на Тогда, сравнив полученный интеграле формулой 9, увидим, что А = 3. Следовательно, получим:
Замечание. Совершенно аналогично следует поступать с интегралами вида
Если в каждом из них мы введем под дифференциал множитель b и разделим интеграл на этот множитель, то приведем данные интегралы к табличным (см. формулы 10, 11, 12 в табл. I), причем и = Ьх.
Решение. Вряд ли кому-нибудь придет в голову мысль возвести данный двучлен в 27-ю степень и затем интегрировать сумму из 28-ми слагаемых, хотя такой путь вполне законен. Данный интеграл берется совсем легко с помощью правила III и формулы I из таблицы I. В самом деле, имеем:
Способ непосредственного интегрирования дает возможность брать интегралы вида
Данный интеграл можно свести к табличному, если ввести множитель 2 под дифференциал и разделить весь интеграл на 2:
В самом деле, так как f'(x)dx =Af (х), то
Итак, если числитель подынтегральной функщш равен производной ее знаменателя (или отличается от нее постоянным множителем), то интеграл равен логарифму модуля знаменателя плюс произвольная постоянная.
9. Найти интеграл: так как функция cos л: в числителе есть производная знаменателя sin х.
Применяя к равенству (2) правило III, мы легко возьмем и более сложный интеграл:
Так как производная знаменателя равна 6*, то достаточно в первом интеграле помножить числитель на 6, а весь интеграл разделить на 6:
Второй интеграл равенства (3) берется аналогично интегралу задачи 7:
так как после умножения числителя на 3 он стал равен производной знаменателя.
так как числитель подынтегральной функции равен производной знаменателя.
В задачах 13—26, пользуясь формулами таблицы I и правилами интегрирования I и II, найти заданные интегралы.
Указание. В задаче 25 числитель I подынтегральной функции замените по формуле I = sin2 х 4- cos8 х и разделите почленно на знаменатель. В задаче 26 воспользуйтесь формулой cos 2;r = cos8 х — — Sin2X и разложите на множители.
В задачах 27 — 30 найти интегралы, предварительно исключив целую часть рациональной дроби.
В задачах 29—41, пользуясь правилом интегрирования III или подведением под знак дифференциала, найти заданные интегралы.
При решении задач 42—47 посмотрите решения задач 9—12.
Указание. При решении задачи 43 воспользуйтесь указанием к задаче 25.
В задачах 48, 49 подведите предварительно числитель подынтегральной функции под знак дифференциала.
В задачах 50, 51 подведите предварительно множители х, х% под знак дифференциала.
Что такое непосредственное интегрирование
Вычисление неопределенных интегралов с помощью таблицы интегралов и их основных свойств называется непосредственным интегрированием.
Пример 1. Найдем интеграл
Применив второе и пятое свойства неопределенного интеграла, получим
Далее, используя формулы II , Ш, IV , VIII таблицы и третье свойство интегралов, находим каждый из слагаемых интегралов отдельно:
Проверим результат дифференцированием. Найдем производную полученного выражения:
Мы получили подынтегральную функцию, это доказывает, что интегрирование выполнено верно.
В таблице интегралов приведено следствие III а из формулы III :
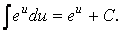
Чтобы воспользоваться этим следствием, найдем дифференциал функции, стоящей в показателе степени:
Для создания этого дифференциала достаточно домножить знаменатель дроби под интегралом на число 2 (очевидно, чтобы дробь не изменилась, необходимо при этом умножить на 2 и числитель). После вынесения постоянного множителя за знак интеграла он становится готовым для применения табличной формулы III а :
следовательно, интегрирование выполнено правильно.
Так как из выражения, стоящего в числителе, можно сконструировать дифференциал квадратичной функции, то следует выделить в знаменателе такую функцию:
Для создания ее дифференциала 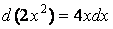
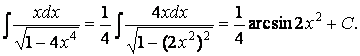
т.е. интегрирование выполнено верно.
Заметим, что теперь квадратичная функция, дифференциал которой 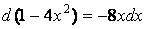
Вывод: интеграл найден правильно.
Обратим внимание на то, что подынтегральное выражение содержит
Поэтому разумно представить дробь в виде степени:
Тогда после домножения числителя и знаменателя на (-1) мы получим степенной интеграл (табличная формула I ):
Дифференцированием результата убеждаемся, что интегрирование выполнено верно.
Легко убедиться, что в этом интеграле из выражения 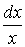
где k —константа. Зато, по опыту примера 3, можно сконструировать интеграл, совпадающий по виду с формулой X из таблицы интегралов:
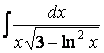
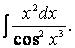
Обратим внимание на то, что в числителе легко создается дифференциал кубической функции d ( x 3 ) = 3 x 2 dx . После чего мы получаем возможность использовать табличную формулу VI :
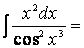
Известно, что производной функции arcsin x является дробь
воспользуемся той же табличной формулой I и тем, что
Пример 11. Для нахождения интеграла
воспользуемся последовательно: тригонометрической формулой
и формулой II таблицы интегралов:
Заметим, что степень переменной в числителе на единицу меньше, чем в знаменателе. Это позволяет в числителе создать дифференциал знаменателя. Найдем

После вынесения постоянного множителя за знак интеграла домножим числитель и знаменатель подынтегральной дроби на (-7), получим:
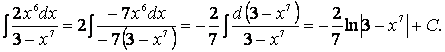
(Здесь использовалась та же формула II из таблицы интегралов).
Пример 14. Найдем интеграл
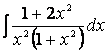
Представим числитель в ином виде: 1 + 2х 2 = (1 + х 2 ) + х 2 и выполним почленное деление, после чего используем пятое свойство интегралов и формулы I и VIII таблицы:
Вынесем постоянный множитель за знак интеграла, вычтем и прибавим в числителе 5, затем выполним почленное деление числителя на знаменатель и воспользуемся пятым свойством интеграла:
Для вычисления первого интеграла используем третье свойство интегралов, а второй интеграл представим в виде, удобном для применения формулы IX :
Отметим, что показатель степени переменной в числителе на единицу меньше, чем в знаменателе (что характерно для производной), а значит, в числителе можно сконструировать дифференциал знаменателя. Найдем дифференциал выражения, стоящего в знаменателе:
Здесь мы использовали II табличный интеграл.
Рассмотрим подобную же ситуацию в следующем примере.
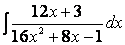
Вычислим дифференциал знаменателя:
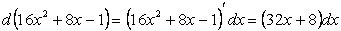
Создадим его в числителе с помощью четвертого свойства интегралов:
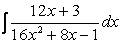
=
Более сложная подобная ситуация будет рассмотрена в примере 19.
Выделим в знаменателе полный квадрат:
После выделения полного квадрата в знаменателе мы получили интеграл, близкий по виду к формулам VIII и IX таблицы интегралов, но в знаменателе формулы VIII слагаемые полные квадраты имеют одинаковые знаки, а в знаменателе нашего интеграла знаки слагаемых различны, хотя и не совпадают со знаками девятой формулы. Добиться полного совпадения знаков слагаемых в знаменателе со знаками в формуле IX удается вынесением коэффициента (-1) за интеграл. Итак, чтобы применить формулу IX таблицы интегралов, проведем следующие мероприятия:
1) вынесем (-1) за скобки в знаменателе и затем за интеграл;
2) найдем дифференциал выражения
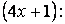
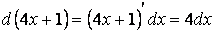
3) создадим в числителе найденный дифференциал;
4) представим число 2 в виде, удобном для применения формулы IX таблицы:
Используя IX формулу таблицы интегралов, получим
Используя опыт, приобретенный при отыскании интегралов в предыдущих двух примерах, и полученные в них результаты, будем иметь
Обобщим некоторый опыт, полученный в результате решения примеров 17,18,19.
Итак, если мы имеем интеграл вида
( пример 19 ) после создания в числителе производной знаменателя распадается на два интеграла: первый – вида
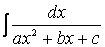
Подкоренное выражение имеет вид выражения
Для применения формулы XI в числителе должен стоять дифференциал
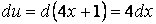
поэтому следует создать его, домножив числитель и знаменатель дроби на число 4:
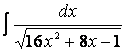
Пример 21. Найдем теперь
Используя опыт предыдущих примеров, создадим в числителе дифференциал знаменателя и разобьем интеграл на два, вынеся ненужные числовые коэффициенты за интегралы:
Первый интеграл перепишем в виде степенного (т.е. в виде 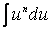
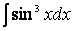
Теперь выразим sin 2 x через cos x и внесем знак минус в скобки:
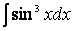
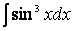
Аналогично поступают всегда при вычислении интегралов вида
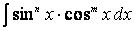
если один из показателей степени положительное нечетное число, а второй—произвольное действительное число ( пример 23).
Используя опыт предыдущего примера и тождество
cos 4 x = (cos 2 x ) 2 = (l — sin 2 x) 2 = 1— 2sin 2 x + sin 4 x,
Выполнив почленное деление слагаемых числителя на знаменатель, будем иметь
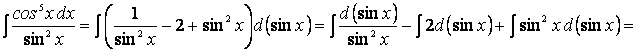
При интегрировании четных степеней тригонометрических функций сначала следует по возможности понизить степень, используя известные формулы:
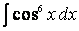
Преобразуем подынтегральную функцию:
Подставив полученную сумму под интеграл, получим