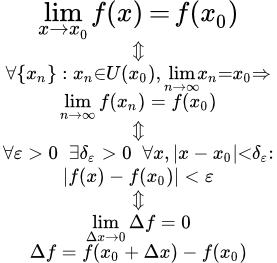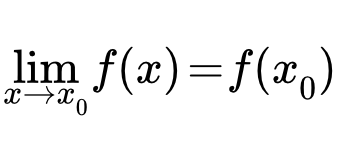Что такое непрерывность функции в точке

Определение непрерывности функции в точке

Непрерывность в точке

Определение непрерывности

Определение непрерывности функции в точке
Функция f ( x ) называется непрерывной в точке x ₀ , если она определена на некоторой окрестности U ( x ₀) этой точки, включая саму точку, и если предел при x стремящемся к x ₀ существует и равен значению функции в x ₀ :
.

Здесь подразумевается, что x ₀ – это конечная точка. Значение функции в ней может быть только конечным числом.

Если привлечь сюда определение конечного предела функции в конечной точке, то можно дать развернутую формулировку определения непрерывности функции. Поскольку имеется два равносильных определения предела функции (по Коши и по Гейне), то можно дать, как минимум, еще два эквивалентных определения непрерывности.

Запишем эти определения с помощью логических символов существования и всеобщности.
По Гейне:
.
По Коши:
.

Определение отсутствия непрерывности

Непрерывность на концах отрезка

Определение непрерывности справа (слева)
Функция f ( x ) называется непрерывной справа (слева) в точке x ₀ , если она определена на некоторой правосторонней (левосторонней) окрестности этой точки, и если правый (левый) предел в точке x ₀ равен значению функции в x ₀ :
.

Примеры

Пример 1

Используем определение по Гейне

Используем определение по Коши

Пример 2

Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Источник

Непрерывность функций – теоремы и свойства

Определение непрерывности функции

Определение непрерывности справа (слева)
Функция f ( x ) называется непрерывной справа (слева) в точке x ₀ , если она определена на некоторой правосторонней (левосторонней) окрестности этой точки, и если правый (левый) предел в точке x ₀ равен значению функции в x ₀ :
.

Свойства непрерывных в точке функций

Свойство непрерывности слева и справа
Функция непрерывна в точке тогда и только тогда, когда она непрерывна в справа и слева.

Доказательства свойств приводятся на странице «Свойства непрерывных в точке функций».

Непрерывность сложной функции

Предел сложной функции

Точки разрыва

Определение точки разрыва 1-го рода
Точка называется точкой разрыва первого рода, если является точкой разрыва и существуют конечные односторонние пределы слева и справа :
.

Определение скачка функции
Скачком Δ функции в точке называется разность пределов справа и слева
.

Таким образом, точка устранимого разрыва – это точка разрыва 1-го рода, в которой скачек функции равен нулю.

Определение точки разрыва 2-го рода
Точка называется точкой разрыва второго рода, если она не является точкой разрыва 1-го рода. То есть если не существует, хотя бы одного одностороннего предела, или хотя бы один односторонний предел в точке равен бесконечности.

Свойства функций, непрерывных на отрезке

Вторая теорема Вейерштрасса о максимуме и минимуме непрерывной функции
Непрерывная на отрезке функция достигает на нем своих верхней и нижней граней или, что тоже самое, достигает на отрезке своего максимума и минимума.

Обратные функции

Аналогичным образом можно сформулировать теорему о существовании и непрерывности обратной функции на полуинтервале.

Свойства и непрерывность элементарных функций

Элементарные функции и обратные к ним непрерывны на своей области определения. Далее мы приводим формулировки соответствующих теорем и даем ссылки на их доказательства.

Показательная функция

Логарифм

Экспонента и натуральный логарифм

Степенная функция

Тригонометрические функции

Теорема о непрерывности тригонометрических функций
Тригонометрические функции: синус ( sin x ), косинус ( cos x ), тангенс ( tg x ) и котангенс ( ctg x ), непрерывны на своих областях определения.

Теорема о непрерывности обратных тригонометрических функций
Обратные тригонометрические функции: арксинус ( arcsin x ), арккосинус ( arccos x ), арктангенс ( arctg x ) и арккотангенс ( arcctg x ), непрерывны на своих областях определения.

Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Источник