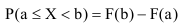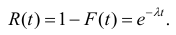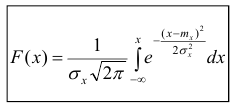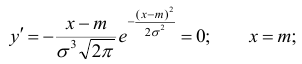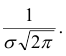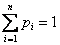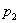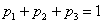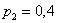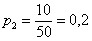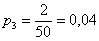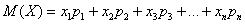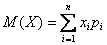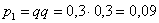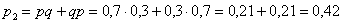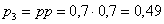Что такое непрерывные величины

Содержание:

Непрерывные случайные величины: функция распределения случайной величины:

Если вычислить вероятность появления непрерывной случайной величины не составляет особого труда, то решение основной задачи теории вероятностей для непрерывной случайной величины несёт большие трудности. Поэтому в материалах сегодняшней лекции мы рассмотрим методы определения вероятности попадания непрерывной случайной величины на интервал с помощью функции распределения.

Функция распределения непрерывной случайной величины

Зная функцию распределения непрерывной случайной величины, задача определения вероятности её попадания на интервал (а; b) может быть решена следующим образом.

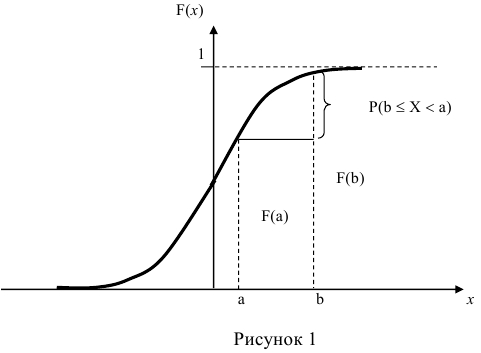
По известной функции распределения вероятность попадания непрерывной случайной величины на интервал (а; b) равна приращению функции распределения на этом участке (рис. 1).

Во всех рассмотренных выше случаях случайная величина определялась путём задания значений самой величины и вероятностей этих значений.

Однако такой метод применим далеко не всегда. Например, в случае непрерывной случайной величины, её значения могут заполнять некоторый произвольный интервал. Очевидно, что в этом случае задать все значения случайной величины просто нереально.

Даже в случае, когда это сделать можно, зачастую задача решается чрезвычайно сложно. Рассмотренный только что пример даже при относительно простом условии (приборов только четыре) приводит к достаточно неудобным вычислениям, а если в задаче будет несколько сотен приборов?

Поэтому встает задача по возможности отказаться от индивидуального подхода к каждой задаче и найти по возможности наиболее общий способ задания любых типов случайных величин.

Функция надежности

Определение. Функцией надёжности R(t) называют функцию, определяющую вероятность безотказной работы устройства в течение времени t.

Часто на практике длительность безотказной работы подчиняется показательному закону распределению.

Вообще говоря, если рассматривать новое устройство, то вероятность отказа в начале его функционирования будет больше, затем количество отказов снизится и будет некоторое время иметь практически одно и то же значение. Затем (когда устройство выработает свой ресурс) количество отказов будет возрастать.

Другими словами, можно сказать, что функционирование устройства на протяжении всего существования (в смысле количества отказов) можно описать комбинацией двух показательных законов (в начале и конце функционирования) и равномерного закона распределения.

Функция надёжности для какого- либо устройства при показательном законе распределения равна:

Данное соотношение называют показательным законом надежности.

Важным свойством, позволяющим значительно упростить решение задач теории надежности, является то, что вероятность безотказной работы устройства на интервале времени t не зависит от времени предшествующей работы до начала рассматриваемого интервала, а зависит только от длительности времени t.

Таким образом, безотказная работа устройства зависит только от интенсивности отказов 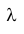и не зависит от безотказной работы устройства в
прошлом.

Так как подобным свойством обладает только показательный закон распределения, то этот факт позволяет определить, является ли закон распределения случайной величины показательным или нет.

Нормальный закон распределения

Определение. Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности

Нормальный закон распределения также называется законом Гаусса.

Нормальный закон распределения занимает центральное место в теории вероятностей. Это обусловлено тем, что этот закон проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. К нормальному закону приближаются все остальные законы распределения.

Можно легко показать, что параметры 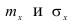входящие в плотность распределения являются соответственно математическим ожиданием и среднеквадратическим отклонением случайной величины X.

Найдём функцию распределения F(x).

График плотности нормального распределения называется нормальной кривой или кривой Гаусса.

Нормальная кривая обладает следующими свойствами:

1) Функция определена на всей числовой оси.

2) При всех х функция распределения принимает только положительные значения.

3) Ось ОХ является горизонтальной асимптотой графика плотности вероятности, т.к. при неограниченном возрастании по абсолютной величине аргумента л\ значение функции стремится к нулю.

4) Найдём экстремум функции.

Т.к. при 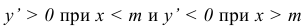, то в точке х = m функция имеет максимум, равный

5) Функция является симметричной относительно прямой x = а, т.к. разность

6) Для нахождения точек перегиба графика найдем вторую производную функции плотности.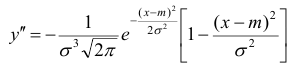

При 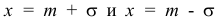вторая производная равна нулю, а при переходе через эти точки меняет знак, т.е. в этих точках функция имеет перегиб.

В этих точках значение функции равно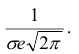
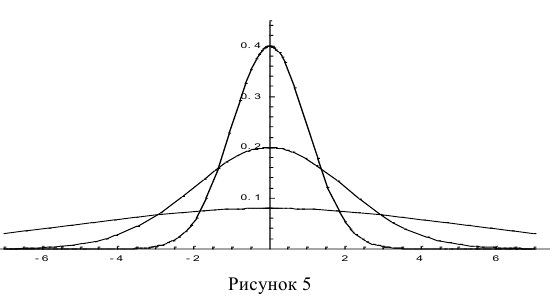
Построим график функции плотности распределения (рис. 5).

Построены графики при м =0 и трёх возможных значениях среднеквадратичного отклонения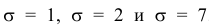. Как видно, при увеличении значения среднего квадратичного отклонения график становится более пологим, а максимальное значение уменьшается.

Если а > 0, то график сместится в положительном направлении, если а

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Что такое непрерывные величины

Законы распределения непрерывных случайных величин разнообразны. В социотехнических системах многие переменные величины могут иметь нормальное распределение. Гипотеза о том, что величины имеют нормальное распределение, служит основой многих оценок в экономической статистике, в маркетинговых исследованиях, при аудиторских проверках. Но если гипотеза не проверена, то результаты оценок можно и следует подвергать сомнению. [c.45]

Риски, связанные с непрерывными случайными величинами [c.63]

Риск ошибки первого рода для количественного признака непрерывной случайной величины, которая не должна превосходить некоторые пределы, определяется как [c.64]

Непрерывная случайная величина может принимать все возможные значения и задаваться в виде функции плотности вероятности. Одним из наиболее простых примеров служит величина, равномерно распределенная по некоторому интервалу, т.е. принимающая все значения из этого интервала с равной вероятностью и не принимающая значений вне этого интервала. [c.262]

В формуле для определения математического ожидания непрерывной случайной величины вместо вероятности используется функция плотности вероятности [c.263]

Здесь X, Y — дискретные случайные величины, a Z — непрерывная случайная величина. [c.25]

Если все значения непрерывной случайной величины в некотором интервале от а до b, равновероятны, то аналитически это можно записать в виде р(х) = О х Ь [c.33]

Рассмотрим две непрерывные случайные величины X и Y. Тогда вероятность того, что в некотором испытании величина X [c.91]

Непрерывная случайная величина подобным образом не может быть охарактеризована по двум причинам [c.131]

И НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН [c.41]

Для непрерывной случайной величины функция распределе- [c.42]

Для непрерывной случайной величины математическое ожи- [c.44]

Непрерывная случайная величина X, которая может прини- [c.53]

Непрерывные случайные величины 332 [c.476]

Матем этическое ожидание и дисперсия непрерывной случайной величины с плотностью вероятности

Источник

Что такое непрерывные величины

1. Формирование представление о случайной величине, дискретных и непрерывных случайных величинах.

2. Знакомство с законом распределения дискретной случайной величины, функцией распределения и плотностью распределения непрерывной случайной величины, числовых характеристиках случайных величин.

1. Виды случайных величин.

2. Закон распределения дискретной случайной величины.

3. Функция распределения вероятностей случайной величины.

4. Плотность распределения вероятностей непрерывной случайной величины.

5. Математическое ожидание.

6. Дисперсия и среднеквадратическое отклонение.

1. Виды случайных величин.

Случайной величиной называется такая величина, которая случайно принимает какое-то значение из множества возможных значений.

По множеству возможных значений различают дискретные и непрерывные случайные величины.

Дискретными называются случайные величины, значениями которых являются только отдельные точки числовой оси. (Число их может быть как конечно, так и бесконечно).

Пример: Число родившихся девочек среди ста новорожденных за последний месяц- это дискретная случайная величина, которая может принимать значения 1,2,3,…

Непрерывными называются случайные величины, которые могут принимать все значения из некоторого числового промежутка.

2. Закон распределения дискретной случайной величины.

Закон распределения дискретной случайной величины— это соответствие между возможными значениями случайной величины и их вероятностями.

Закон распределения можно задать таблично, аналитически, графически.

При задании закона распределения таблично, в первую строку таблицы вносятся возможные значения случайно величины, а во вторую- их вероятности.

Пример: Монету подбросили 3 раза. Запишите закон распределения числа выпадения «герба».

Возможные значения данной случайной величины: 0, 1, 2, 3.

Найдем вероятность того, что «герб» не появится (0 раз).

Найдем вероятность того, что «герб» появится 1 раз.

Найдем вероятность того, что «герб» появится 2 раза.

Найдем вероятность того, что «герб» появится 3 раза.

Тогда закон распределения данной дискретной случайной величины можно представить таблицей:

Для наглядности закон распределения дискретной случайной величины можно изобразить графически, для чего в прямоугольной системе координат строят точки с координатами (x_i ; p_i), а затем соединяют их отрезками прямых. Полученная фигура называется многоугольником распределения.

Однако, такой способ задания (перечисление всех возможных значений случайной величины и их вероятностей) не подходит для непрерывных случайных величин. Составить перечень их возможных значений невозможно.

3. Функция распределения вероятностей случайной величины.

Дадим новый способ задания любых типов случайных величин. С этой целью введем функцию распределения вероятностей случайной величины.

Функцией распределения случайной величины называют функцию F ( x ), определяющую вероятность того, что случайная величина Х в результате испытания примет значение меньшее х, т.е. F ( x ) P ( X x ).

Геометрически это равенство можно истолковать так: F ( x ) –есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х.

Иногда вместо термина «функция распределения» используется термин «интегральная функция».

Свойства функции распределения:

Следствие 1: Вероятность того, что случайная величина примет значение, заключенное в интервале (а; b ), равна приращению функции распределения на этом интервале:

Пример: Случайная величина Х задана функцией распределения:

Найдите вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0; 2).

Следствие: Если возможные значения непрерывной случайной величины распределены на всей числовой оси, то справедливы следующие предельные соотношения:

Рассмотренные выше свойства позволяют представить, как выглядит график функции распределения непрерывной случайной величины.

График расположен в полосе, ограниченной прямыми у=0, у=1 (1 свойство).

4. При возрастании значения х в интервале ( a ; b ), в котором заключены все возможные значения случайной величины, график растет вверх (2 свойство).

5. При ординаты графика равны 0, при ординаты графика равны 1 (3 свойство).

Замечание: График функции распределения дискретной случайной величины имеет ступенчатый вид.

Пример: Дискретная случайная величина Х задана таблицей распределения:

Найдите функцию распределения и постройте ее график.

Итак, функция распределения имеет следующий вид:

4. Плотность распределения вероятностей непрерывной случайной величины.

Непрерывную случайную величину можно также задать, используя другую функцию, которую называют плотностью распределения или плотностью вероятности (дифференциальной функцией).

Плотность распределения вероятностей непрерывной случайной величины Х называют функцию f ( x )- первую производную от функции распределения F ( x ).

Пример: Задана плотность вероятностей случайной величины Х.

Найдите вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0,5; 1).

Свойства плотности распределения вероятностей:

Свойство 1: Плотность распределения- неотрицательная функция: f ( x ) > 0.

Часто, для того чтобы характеризовать случайную величину используют числа, которые описывают случайную величину суммарно. Такие числа называются числовыми характеристиками случайной величины. К числу важнейших числовых характеристик относятся математическое ожидание и дисперсия.

5. Математическое ожидание.

Математическое ожидание приближенно равно среднему значению случайной величины. Например, если известно, что математическое ожидание числа выбиваемых очков у первого стрелка больше, чем у второго, то первый стрелок в среднем выбивает больше очков, чем второй, и следовательно стреляет лучше.

Пример: Найдите математическое ожидание, зная закон распределения дискретной случайной величины.

Источник

Что такое непрерывные величины

§ 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

3.3. Непрерывные случайные величины.

Кроме дискретных случайных величин, возможные значения которых образуют конечную или бесконечную последовательность чисел, не заполняющих сплошь никакого интервала, часто встречаются случайные величины, возможные значения которых образуют некоторый интервал. Примером такой случайной величины может служить отклонение от номинала некоторого размера детали при правильно налаженном технологическом процессе. Такого рода, случайные величины не могут быть заданы с помощью закона распределения вероятностей р(х). Однако их можно задать с помощью функции распределения вероятностей F(х). Эта функция определяется точно так же, как и в случае дискретной случайной величины:

Таким образом, и здесь функция F(х) определена на всей числовой оси, и ее значение в точке х равно вероятности того, что случайная величина примет значение, меньшее чем х.

Формула (19) и свойства 1° и 2° справедливы для функции распределения любой случайной величины. Доказательство проводится аналогично случаю дискретной величины.

Случайная величина называется непрерывной, если для нее существует неотрицательная кусочно-непрерывная функция* , удовлетворяющая для любых значений x равенству

(22)

Функция называется плотностью распределения вероятностей, или кратко, плотностью распределения. Если x₁

Так как , а на основании формулы (22)

, то

(24)

Пользуясь формулой (22), найдем как производную интеграла по переменной верхней границе, считая плотность распределения непрерывной**:

(25)

Заметим, что для непрерывной случайной величины функция распределения F(х) непрерывна в любой точке х, где функция непрерывна. Это следует из того, что F(х) в этих точках дифференцируема.

На основании формулы (23), полагая x₁=x, , имеем

В силу непрерывности функции F(х) получим, что

Таким образом, вероятность того, что непрерывная случайная величина может принять любое отдельное значение х, равна нулю.

Отсюда следует, что события, заключающиеся в выполнении каждого из неравенств

, , ,

Имеют одинаковую вероятность, т.е.

В самом деле, например,

так как

Замечание. Как мы знаем, если событие невозможно, то вероятность его наступления равна нулю. При классическом определении вероятности, когда число исходов испытания конечно, имеет место и обратное предложение: если вероятность события равна нулю, то событие невозможно, так как в этом случае ему не благоприятствует ни один из исходов испытания. В случае непрерывной случайной величины число возможных ее значений бесконечно. Вероятность того, что эта величина примет какое-либо конкретное значение x₁ как мы видели, равна нулю. Однако отсюда не следует, что это событие невозможно, так как в результате испытания случайная величина может, в частности, принять значение x₁. Поэтому в случае непрерывной случайной величины имеет смысл говорить о вероятности попадания случайной величины в интервал, а не о вероятности того, что она примет какое-то конкретное значение.

Так, например, при изготовлении валика нас не интересует вероятность того, что его диаметр будет равен номиналу. Для нас важна вероятность того, что диаметр валика не выходит из поля допуска.

Пример. Плотность распределения непрерывной случайной величины задана следующим образом:

График функции представлен па рис. 7. Определить вероятность того, что случайная величина примет значение, удовлетворяющее неравенствам .Найти функцию распределения заданной случайной величины. (Решение)

Следующие два пункта посвящены часто встречающимся на практике распределениям непрерывных случайных величин — равномерному и нормальному распределениям.

Дальше. * Функция называется кусочно-непрерывной на всей числовой оси, если она на любом сегменте или непрерывна, или имеет конечное число точек разрыва I рода.

** Правило дифференцирования интеграла с переменной верхней границей, выведенное в случае конечной нижней границы, остается справедливым и для интегралов с бесконечной нижней границей. В самом деле,

Источник

Случайные величины. Дискретная случайная величина.
Математическое ожидание

Второй раздел по теории вероятностей посвящён случайным величинам, которые незримо сопровождали нас буквально в каждой статье по теме. И настал момент чётко сформулировать, что же это такое:

Случайной называют величину, которая в результате испытания примет одно и только одно числовое значение, зависящее от случайных факторов и заранее непредсказуемое.

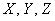
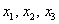
Случайные величины, как правило, обозначают через *, а их значения – соответствующими маленькими буквами с подстрочными индексами, например, .

* Иногда используют 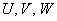, а также греческие буквы

Пример встретился нам на первом же уроке по теории вероятностей, где мы фактически рассмотрели следующую случайную величину:

– количество очков, которое выпадет после броска игрального кубика.

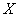
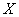
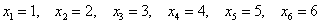
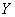
В результате данного испытания выпадет одна и только грань, какая именно – не предсказать (фокусы не рассматриваем); при этом случайная величина может принять одно из следующий значений:

.

– количество мальчиков среди 10 новорождённых.

Совершенно понятно, что это количество заранее не известно, и в очередном десятке родившихся детей может оказаться:

, либо мальчиков – один и только один из перечисленных вариантов.

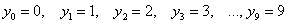
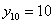
И, дабы соблюсти форму, немного физкультуры:

– дальность прыжка в длину (в некоторых единицах).

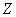
Её не в состоянии предугадать даже мастер спорта 🙂

Тем не менее, ваши гипотезы?

Коль скоро речь идёт о множестве действительных чисел, то случайная величина 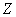может принять несчётно много значений из некоторого числового промежутка. И в этом состоит её принципиальное отличие от предыдущих примеров.

Таким образом, случайные величины целесообразно разделить на 2 большие группы:

1) Дискретная (прерывная) случайная величина – принимает отдельно взятые, изолированные значения. Количество этих значений конечно либо бесконечно, но счётно.

…нарисовались непонятные термины? Срочно повторяем основы алгебры!

2) Непрерывная случайная величина – принимает все числовые значения из некоторого конечного или бесконечного промежутка.

Примечание: в учебной литературе популярны аббревиатуры ДСВ и НСВ

Сначала разберём дискретную случайную величину, затем – непрерывную.

Закон распределения дискретной случайной величины

– это соответствие между возможными значениями этой величины и их вероятностями. Чаще всего закон записывают таблицей:

Довольно часто встречается термин ряд распределения, но в некоторых ситуациях он звучит двусмысленно, и поэтому я буду придерживаться «закона».

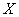
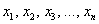
А теперь очень важный момент: поскольку случайная величина обязательно примет одно из значений , то соответствующие события образуют полную группу и сумма вероятностей их наступления равна единице:

или, если записать свёрнуто:

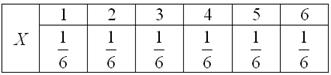
Так, например, закон распределения вероятностей выпавших на кубике очков имеет следующий вид:

Возможно, у вас сложилось впечатление, что дискретная случайная величина может принимать только «хорошие» целые значения. Развеем иллюзию – они могут быть любыми:

Некоторая игра имеет следующий закон распределения выигрыша:

Найти

…наверное, вы давно мечтали о таких задачах 🙂 Открою секрет – я тоже. В особенности после того, как завершил работу над теорией поля.

Решение: так как случайная величина 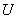может принять только одно из трёх значений, то соответствующие события образуют полную группу, а значит, сумма их вероятностей равна единице:

Разоблачаем «партизана»: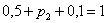

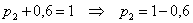
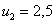
– таким образом, вероятность выигрыша условных единиц составляет 0,4.

Контроль: 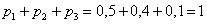, в чём и требовалось убедиться.

Ответ:

Не редкость, когда закон распределения требуется составить самостоятельно. Для этого используют классическое определение вероятности, теоремы умножения / сложения вероятностей событий и другие фишки тервера:

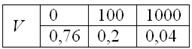
В коробке находятся 50 лотерейных билетов, среди которых 12 выигрышных, причём 2 из них выигрывают по 1000 рублей, а остальные – по 100 рублей. Составить закон распределения случайной величины 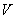– размера выигрыша, если из коробки наугад извлекается один билет.

Решение: как вы заметили, значения случайной величины принято располагать в порядке их возрастания. Поэтому мы начинаем с самого маленького выигрыша, и именно 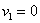рублей.

Всего таковых билетов 50 – 12 = 38, и по классическому определению:
– вероятность того, что наудачу извлечённый билет окажется безвыигрышным.

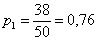
С остальными случаями всё просто. Вероятность выигрыша 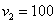рублей составляет:

И для :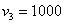

Проверка: 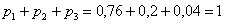– и это особенно приятный момент таких заданий!

Ответ: искомый закон распределения выигрыша:

Следующее задание для самостоятельного решения:

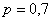
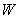
Вероятность того, что стрелок поразит мишень, равна . Составить закон распределения случайной величины – количества попаданий после 2 выстрелов.

…я знал, что вы по нему соскучились 🙂 Вспоминаем теоремы умножения и сложения. Решение и ответ в конце урока.

Закон распределения полностью описывает случайную величину, однако на практике бывает полезно (а иногда и полезнее) знать лишь некоторые её числовые характеристики.

Математическое ожидание дискретной случайной величины

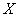
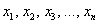
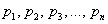
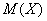
Говоря простым языком, это среднеожидаемое значение при многократном повторении испытаний. Пусть случайная величина принимает значения с вероятностями соответственно. Тогда математическое ожидание данной случайной величины равно сумме произведений всех её значений на соответствующие вероятности:

или в свёрнутом виде:

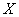
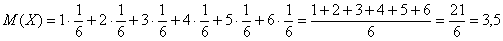
Вычислим, например, математическое ожидание случайной величины – количества выпавших на игральном кубике очков:

очка

В чём состоит вероятностный смысл полученного результата? Если подбросить кубик достаточно много раз, то среднее значение выпавших очков будет близкО к 3,5 – и чем больше провести испытаний, тем ближе. Собственно, об этом эффекте я уже подробно рассказывал на уроке о статистической вероятности.

Теперь вспомним нашу гипотетическую игру:

Возникает вопрос: а выгодно ли вообще играть в эту игру? …у кого какие впечатления? Так ведь «навскидку» и не скажешь! Но на этот вопрос можно легко ответить, вычислив математическое ожидание, по сути – средневзвешенный по вероятностям выигрыш:

, таким образом, математическое ожидание данной игры проигрышно.

Не верь впечатлениям – верь цифрам!

Да, здесь можно выиграть 10 и даже 20-30 раз подряд, но на длинной дистанции нас ждёт неминуемое разорение. И я бы не советовал вам играть в такие игры 🙂 Ну, может, только ради развлечения.

Из всего вышесказанного следует, что математическое ожидание – это уже НЕ СЛУЧАЙНАЯ величина.

Творческое задание для самостоятельного исследования:

Мистер Х играет в европейскую рулетку по следующей системе: постоянно ставит 100 рублей на «красное». Составить закон распределения случайной величины 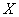– его выигрыша. Вычислить математическое ожидание выигрыша и округлить его до копеек. Сколько в среднем проигрывает игрок с каждой поставленной сотни?

Справка: европейская рулетка содержит 18 красных, 18 чёрных и 1 зелёный сектор («зеро»). В случае выпадения «красного» игроку выплачивается удвоенная ставка, в противном случае она уходит в доход казино

Существует много других систем игры в рулетку, для которых можно составить свои таблицы вероятностей. Но это тот случай, когда нам не нужны никакие законы распределения и таблицы, ибо доподлинно установлено, что математическое ожидание игрока будет точно таким же. От системы к системе меняется лишь дисперсия, о которой мы узнаем во 2-й части урока.

Но прежде будет полезно размять пальцы на клавишах калькулятора:

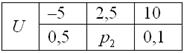
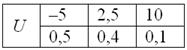
Случайная величина 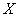задана своим законом распределения вероятностей:

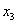
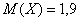
Найти , если известно, что . Выполнить проверку.

Тогда переходим к изучению дисперсии дискретной случайной величины, и по возможности, ПРЯМО СЕЙЧАС!! – чтобы не потерять нить темы.

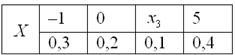
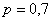
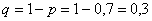
Пример 3. Решение: по условию – вероятность попадания в мишень. Тогда:
– вероятность промаха.

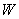
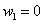
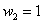
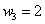
Составим – закон распределения попаданий при двух выстрелах:

– ни одного попадания. По теореме умножения вероятностей независимых событий:

– одно попадание. По теоремам сложения вероятностей несовместных и умножения независимых событий:

– два попадания. По теореме умножения вероятностей независимых событий:

Проверка: 0,09 + 0,42 + 0,49 = 1

Ответ:

Примечание: можно было использовать обозначения 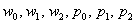– это не принципиально.

Пример 4. Решение: игрок выигрывает 100 рублей в 18 случаях из 37, и поэтому закон распределения его выигрыша имеет следующий вид: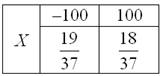

Вычислим математическое ожидание: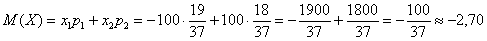

Таким образом, с каждой поставленной сотни игрок в среднем проигрывает 2,7 рубля.

Пример 5. Решение: по определению математического ожидания: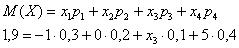

поменяем части местами и проведём упрощения: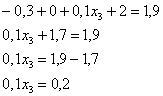

таким образом:

Выполним проверку: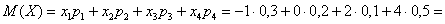

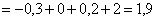
, что и требовалось проверить.

Ответ:

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Tutoronline.ru – онлайн репетиторы по математике и другим предметам

Источник