Что такое неприводимый многочлен

Приводимые и неприводимые многочлены

в кольце Р[х].

Определение 1. Многочлен f(x) ¹ 0 из Р[х] называется приводимым над полем Р, если его можно представить в виде произведения многочленов выше нулевой степени, т.е. f(x) = g(x)×h(x), где cm g(x) 0,

2. f(x) не разлагается в произведение многочленов меньшей степени.

Замечание 1. Многочлены нулевой степени не входят в класс приводимых и неприводимых многочленов, а образуют свой класс, т.е. если множество натуральных чисел мы разбили на три класса:

то и множество Р[х] разбивается на три класса:

1. многочлены нулевой степени (а_iÎР);

2. приводимые многочлены;

3. неприводимые многочлены.

Замечание 2. Приводимость многочленов зависит от поля Р. (смотри прим. 1)

Также как в кольце Z, в кольце Р[х] можно доказать аналог основной теоремы арифметики.

Теорема«f(x) ¹ 0, f(x)ÎP[x], cm f(x)>0 разлагается в произведение неприводимых многочленов единственным способом, с точностью до порядка следования многочленов нулевой степени.

Доказать самостоятельно теорему и следствие из неё.

Следствие. Если f(x) = c₁p₁ a 1 (x) p₂ a 2 (x)×. × p_k a k (x),

Покажем, что задача о разложении многочлена на линейные множители (многочлены первой степени) сводится к задаче нахождения корней многочлена f(x) в поле Р.

Определение 3. Элемент aÎР называют корнем многочлена f(x), если f(a)=0.

Ответ на вопрос о существовании корней многочлена f(x) над полями C, R и Q даёт основная теорема алгебры.

Теорема 1. 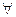f(x) Î C[x], ст f(x) > 1 имеет хотя бы один корень.

Опираясь на эту теорему и определение понятия корня многочлена, можно доказать теорему 2.

Источник

Неприводимый многочлен

Смотреть что такое «Неприводимый многочлен» в других словарях:

Неприводимый многочлен — многочлен, неразложимый на нетривиальные (неконстантные) многочлены. Неприводимые многочлены являются неприводимыми элементами кольца многочленов. Содержание 1 Определение 2 Свойства 3 Примеры … Википедия

НЕПРИВОДИМЫЙ МНОГОЧЛЕН — многочлен, не разлагающийся на множители более низкой степени. Возможность разложить многочлен на множители (и свойство неприводимости) зависит от того, какие числа допускаются в качестве коэффициента многочлена. Так, многочлен х3 + 2 неприводим … Большой Энциклопедический словарь

неприводимый многочлен — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN irreducible polynominal … Справочник технического переводчика

неприводимый многочлен — многочлен, не разлагающийся на множители более низкой степени. Возможность разложить многочлен на множители (и свойство неприводимости) зависит от того, какие числа допускаются в качестве коэффициента многочлена. Так, многочлен х3 + 2 неприводим … Энциклопедический словарь

НЕПРИВОДИМЫЙ МНОГОЧЛЕН — многочлен, не разлагающийся на множители более низкой степени. Возможность разложить многочлен на множители (и. свойство неприводимости) зависит от того, какие числа допускаются в качестве коэф. многочлена. Так, многочлен х3 + 2 неприводим, если… … Естествознание. Энциклопедический словарь

Многочлен Лорана — В математике, многочлены или полиномы от одной переменной функции вида где ci фиксированные коэффициенты, а x переменная. Многочлены составляют один из важнейших классов элементарных функций. Изучение полиномиальных уравнений и их решений… … Википедия

Источник

Неприводимый многочлен иногда называют сводимый. [1] [2] Однако этот термин следует использовать осторожно, так как он может относиться к другим понятиям сокращение.

Неприводимые многочлены естественным образом возникают при изучении полиномиальная факторизация и расширения алгебраических полей.

Полезно сравнить неприводимые многочлены с простые числа: простые числа (вместе с соответствующими отрицательными числами равной величины) являются неприводимыми целые числа. Они демонстрируют многие общие свойства концепции «неприводимости», которые в равной степени применимы к неприводимым многочленам, такие как уникальная факторизация на простые или неприводимые множители. Когда кольцо коэффициентов представляет собой поле или другое уникальная область факторизации, неприводимый многочлен также называется простой многочлен, потому что он генерирует главный идеал.

Содержание

Определение

Если F поле, непостоянный многочлен несводимый по F если его коэффициенты принадлежат F и его нельзя разложить на произведение двух непостоянных многочленов с коэффициентами в F.

Часто используется другое определение, в котором говорится, что многочлен неприводима над R если он неприводим по поле дробей из р (Поле рациональное число, если р это целые числа). Это второе определение не используется в этой статье.

Природа фактора

Простые примеры

Следующие шесть многочленов демонстрируют некоторые элементарные свойства приводимых и неприводимых многочленов:

Над рациональное число, первые два и четвертый многочлены приводимы, но три других многочлена неприводимы (как многочлен над рациональными числами, 3 является единица измерения, и, следовательно, не считается фактором).

Над сложные числа, все шесть многочленов приводимы.

Над комплексными числами

Над сложное поле, и в более общем плане алгебраически замкнутое поле, а одномерный многочлен неприводимо тогда и только тогда, когда его степень является одним. Этот факт известен как основная теорема алгебры в случае комплексных чисел и вообще как условие алгебраической замкнутости.

Отсюда следует, что любой непостоянный одномерный многочлен можно разложить на множители как

Есть несводимые многомерные полиномы каждой степени по комплексным числам. Например, полином

который определяет Кривая Ферма, неприводима для любого положительного п.

По реалам

Уникальное свойство факторизации

Каждый многочлен над полем F можно разложить на произведение ненулевой константы и конечного числа неприводимых (над F ) полиномы. Это разложение уникально вплоть до порядок множителей и умножение множителей на ненулевые константы, произведение которых равно 1.

Это теорема, которая мотивирует, что определение неприводимый многочлен в единственной области факторизации часто предполагает, что многочлен непостоянен.

Все алгоритмы которые в настоящее время реализовано для факторизации многочленов по целые числа и более рациональное число используйте этот результат (см. Факторизация многочленов).

Над целыми числами и конечным полем

Связь между неприводимостью над целыми числами и неприводимостью по модулю п глубже, чем предыдущий результат: на сегодняшний день все реализованные алгоритмы факторизации и несводимости по целым числам и по рациональным числам используют факторизацию по конечным полям как подпрограмма.

В некотором смысле почти все многочлены с коэффициентами ноль или единица неприводимы над целыми числами. Точнее, если версия Гипотеза Римана за Дзета-функции Дедекинда предполагается, что вероятность неприводимости по целым числам многочлена с случайный коэффициенты в <0, 1>стремится к единице при увеличении степени. [5] [6]

Алгоритмы

Уникальное свойство факторизации полиномов не означает, что факторизация данного полинома всегда может быть вычислена. Даже неприводимость полинома не всегда может быть доказана вычислением: есть поля, над которыми не алгоритм могут существовать для определения неприводимости произвольных многочленов. [7]

Алгоритмы факторизации многочленов и определения неприводимости известны и реализованы в системы компьютерной алгебры для многочленов от целых чисел, рациональные числа, конечные поля и конечно порожденное расширение поля этих полей. Все эти алгоритмы используют алгоритмы для факторизация многочленов над конечными полями.

Расширение поля

Понятия неприводимого многочлена и расширение алгебраического поля сильно связаны следующим образом.

Позволять Икс быть элементом расширение L поля K. Этот элемент называется алгебраический если это корень полинома с коэффициентами в K. Среди многочленов, из которых Икс есть корень, есть ровно один моник и минимальной степени, называемые минимальный многочлен из Икс. Минимальный многочлен алгебраического элемента Икс из L неприводим, и является единственным моническим неприводимым многочленом, от которого Икс это корень. Минимальный многочлен от Икс делит каждый многочлен, имеющий Икс как корень (это Теорема Абеля о неприводимости).

Над областью целостности

Если р является область целостности, элемент ж из р который не является ни нулем, ни единицей называется несводимый если нет не юнитов грамм и час с ж = gh. Можно показать, что каждый главный элемент неприводимо; [8] обратное неверно в общем случае, но верно в уникальные домены факторизации. В кольцо многочленов F[Икс] над полем F (или любая область уникальной факторизации) снова является уникальной областью факторизации. Индуктивно это означает, что кольцо многочленов в п неопределенный (над кольцом р) является уникальной факторизационной областью, если то же самое верно для р.

Источник