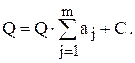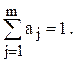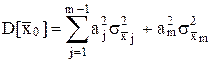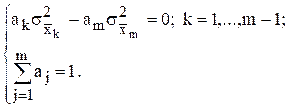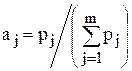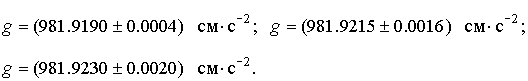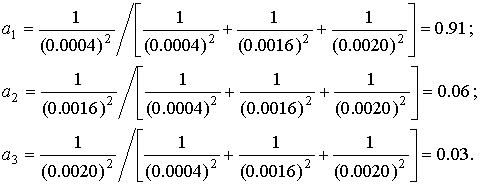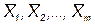Что такое неравнорассеянные наблюдения
В практике исследовательских работ часто встречаются ситуации, когда не-обходимо найти наиболее достоверное значение величины и оценить его возможные отклонения от истинного значения на основании измерений, проводимых разными наблюдателями с применением разнообразных средств измерений и методов измерений в различных лабораториях или условиях внешней среды.
Ряды получающихся при этом результатов наблюдений называются неравнорассеяными (неравноточными), если оценки и их дисперсии значимо отличаются друг от друга, а средние арифметические являются оценками одного и того же значения измеряемой величины.
Если средние неравнорассеянных рядов наблюдения мало отличаются друг от друга, то говорят о высокой воспроизводимости измерений, которая количественно характеризуется рассеиванием результатов.
Рассмотрим некоторые случаи, приводящие к необходимости обработки результатов неравнорассеянных измерений:
1 Если при точных измерениях необходимо убедиться в отсутствии неисключенных систематических погрешностей, то измерения проводятся несколькими исследователями или группами исследователей. Если средние арифметические полученных рядов наблюдений незначимо отличаются друг от друга и ничто не указывает на наличие систематических погрешностей, то можно объединить все полученные результаты и на основе их математической обработки получить более достоверные сведения об измеряемой величине.
2 Аналогичные измерения были выполнены в разных лабораториях различными методами, и получены отличающиеся друг от друга результаты наблюдений. Естественно и в этом случае, используя все имеющиеся данные, попытаться получить более достоверные значения измеряемых величин.
3 Измерения, относящиеся к образцовым мерам и измерительным приборам, часто повторяются через некоторое время. В конце концов накапливаются ряды наблюдений и возникает необходимость объединить их. Точность рядов наблюдений различна, с одной стороны, из-за того, что для впервые проводимых измерений характерно большее рассеивание результатов, а с другой стороны, из-за того, что с течением времени средства измерения стареют или заменяются новыми.
Во всех описанных ситуациях приходится прибегать к методам обработки результатов неравнорассеянных рядов наблюдений, задача которых в общем случае заключается в нахождении наиболее достоверного значения измеряемой величины.
Основой для расчетов служат следующие данные:
1) 
– средние арифметические m рядов неравнорассеянных результатов наблюдений постоянной физической величины Q;
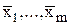
2) 
– оценки с.к.о. результатов наблюдений в отдельных рядах;
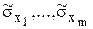
3) n1,…,nm – количество наблюдений в каждом ряду;
Для отыскивания вида этой функции возьмем производную от нее по истинному значению Q измеряемой величины: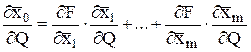 
.
Поскольку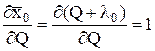 
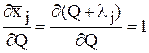
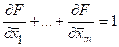
и 
; j =1,…,m, то предыдущее равенство можно записать в следующем виде: 
.
Ни одна из стоящих в этом равенстве производных не может зависеть от значений средних арифметических исходных рядов наблюдений. Однако эти средние арифметические, будучи получены в различных условиях и, может быть, не одним исследователем с помощью различных средств измерений, являются независимыми величинами, которые объединяет лишь общность их математического ожидания. Поэтому производные могут быть только постоянными величинами и искомая функция должна иметь вид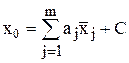 
.
Возьмем математическое ожидание обеих частей этого равенства:
.
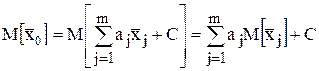
Для того чтобы оценка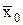 
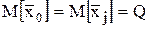
истинного значения была несмещенной, необходимо выполнение условия 
.
Поэтому 
Полученное соотношение выполняется только в том случае, когда
С=0 ; 
Таким образом, окончательно получаем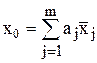 
; 
.
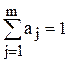
Величина 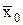называется средним взвешенным, а коэффициенты aj называются весовыми коэффициентами исходных средних арифметических. Именно они и характеризуют степень доверия соответствующему ряду наблюдений.
Желательно так выбрать весовые коэффициенты, чтобы они обращали в минимум дисперсию среднего взвешенного. Последняя составляет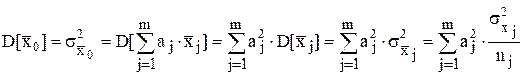 
,
где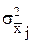 
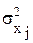
– дисперсия j-го среднего арифметического, которая в nj раз меньше дисперсии 
j-го ряда наблюдения. 
выразим m– й весовой коэффициент через все остальные: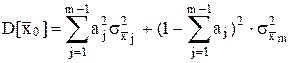 
.
Найдем производную от дисперсии по k–му весовому коэффициенту, где k=1,…, m–1, и приравняем ее к нулю:
.
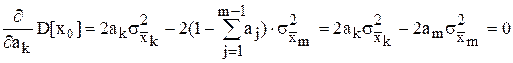
Теперь можно записать систему из m уравнений с m неизвестными коэффициентами 
Подставляя значения m–1 первых весовых коэффициентов из первых уравнений в последнее уравнение, получим выражение для последнего коэффициента
.
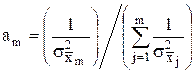
Аналогично из m–1 первых уравнений системы находят и остальные весовые коэффициенты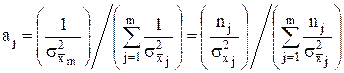 
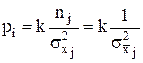
. Величина 
называется весом j–го среднего арифметического, причем коэффициент k может быть любым числом, как размерным, так и безразмерным. В выражениях для весовых коэффициентов этот коэффициент пропадает, поэтому он не сказывается на вычислениях среднего взвешенного и его дисперсии. 
Веса средних арифметических вычислить значительно проще, чем весовые коэффициенты, поэтому имеет смысл записать выражение для среднего взвешенного через отдельные веса: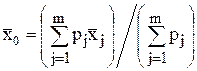 
.
Подставив далее значения весовых коэффициентов, получим значение дисперсии и соответственно с.к.о. среднего взвешенного: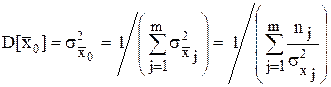 
, из которого, в частности, следует, что дисперсия среднего взвешенного меньше дисперсии всех средних арифметических, если веса выбраны прямо пропорциональными числам измерений в отдельных рядах и обратно пропорциональными их дисперсиям, или, что то же самое, обратно пропорциональными квадратам с.к.о. средних арифметических исходных рядов наблюдений.
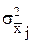
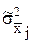
Если теоретические дисперсии неизвестны, то пользуются их оценками 
, с помощью которых определяют веса или весовые коэффициенты.
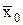
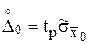
Доверительные границы случайной погрешности для результата измерения , полученного при обработке неравнорассеянных рядов наблюдений, находятся по формуле 
.
Если n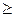
30, значение tp прямо выбирается из таблиц. Если же n Поделись с друзьями
Что такое неравнорассеянные наблюдения
В практике исследовательских работ часто встречаются ситуации, когда необходимо найти наиболее достоверное значение величины и оценить его возможные отклонения от истинного значения на основании измерений, проводимых разными наблюдателями с применением разнообразных измерительных средств и методов измерений в различных лабораториях или условиях внешней среды.
Ряды получающихся при этом результатов наблюдений называются неравнорассеянными, если оценки их дисперсий значительно отличаются друг от друга, а средние арифметические являются оценками одного и того же значения измеряемой величины.
Если средние неравнорассеянных рядов наблюдений мало отличаются друг от друга, то говорят о высокой воспроизводимости измерений, которая количественно характеризуется параметрами рассеивания результатов.
Рассмотрим некоторые случаи, приводящие к необходимости обработки результатов неравнорассеянных измерений:
1. Если при точных измерениях необходимо убедиться в отсутствии неисключенных систематических погрешностей, то измерения проводятся несколькими исследователями или группами исследователей. Если средние арифметические полученных рядов наблюдений незначительно отличаются друг от друга и ничто не указывает на наличие систематических погрешностей, то заманчиво объединить все полученные результаты и на основе их математической обработки получить более достоверные сведения об измеряемой величине.
2. Аналогичные измерения были выполнены в разных лабораториях различными методами и получены отличающиеся друг от друга результаты. Естественно и в этом случае, используя все имеющиеся данные, попытаться получить более достоверные значения измеряемых величин.
3. Измерения, относящиеся к образцовым мерам и измерительным приборам, часто повторяются через некоторое время. В конце концов накапливаются ряды наблюдений и возникает необходимость объединить их. Точность рядов наблюдений различна, с одной стороны, из-за того, что для впервые проводимых измерений характерно большее рассеивание результатов, а с другой стороны, из-за того, что с течением времени средства измерения стареют или заменяются новыми.
Во всех описанных ситуациях приходится прибегать к методам обработки результатов неравнорассеянных рядов наблюдений, задача которых в общем случае заключается в нахождении наиболее достоверного значения измеряемой величины и оценки воспроизводимости измерений.
Для практической обработки результатов неравнорассеянных рядов наблюдений необходимо ввести параметр вес отдельных средних арифметических :
Веса характеризуют степень нашего доверия к соответствующим рядам наблюдений. Чем больше число наблюдений в каждом данном ряду и чем меньше дисперсия результатов наблюдений, тем больше степень доверия к полученному при этом среднему арифметическому и с тем большим весом оно будет учтено при определении оценки истинного значения измеряемой величины
Иногда удобно пользоваться безразмерными весовыми коэффициентами
тогда выражение для среднего взвешенного приобретает простой вид
В соответствии со свойствами оценок максимального правдоподобия дисперсия среднего взвешенного должна равняться единице, деленной на математическое ожидание второй производной от логарифмической функции правдоподобия:
Отсюда следует, что дисперсия среднего взвешенного меньше дисперсии любого из исходных средних арифметических отдельных рядов наблюдений и поэтому при обработке неравнорассеянных рядов наблюдений точность измерений повышается.
При малом числе нормально распределенных результатов наблюдений пользуются распределением Стьюдента с числом степеней свободы
Если же об исходных распределениях нет никаких заслуживающих внимания данных, то на основании центральной предельной теоремы можно все-таки предполагать, что распределение среднего взвешенного нормально, поскольку оно является суммой большого числа случайных величин с конечными дисперсиями и математическими ожиданиями.
Пример. Тремя коллективами экспериментаторов с помощью различных методов измерения были получены следующие значения ускорения свободного падения (со среднеквадратическими отклонениями результатов измерений):
Весовые коэффициенты отдельных результатов вычислим по формуле (68):
Среднее взвешенное в соответствии с уравнением (69) составляет:
Обработка неравнорассеянных рядов наблюдений
В практике исследовательских работ часто встречаются ситуации, когда необходимо найти наиболее достоверное значение величины и оценить его возможные отклонения от истинного значения на основании измерений, проводимых разными наблюдателями с применением разнообразных измерительных средств и методов измерений в различных лабораториях или условиях внешней среды.
Ряды получающихся при этом результатов наблюдений называются неравнорассеянными, если оценки их дисперсий значительно отличаются друг от друга, а средние арифметические являются оценками одного и того же значения измеряемой величины.
Если средние неравнорассеянных рядов наблюдений мало отличаются друг от друга, то говорят о высокой воспроизводимости измерений, которая количественно характеризуется параметрами рассеивания результатов.
Рассмотрим некоторые случаи, приводящие к необходимости обработки результатов неравнорассеянных измерений:
1. Если при точных измерениях необходимо убедиться в отсутствии неисключенных систематических погрешностей, то измерения проводятся несколькими исследователями или группами исследователей. Если средние арифметические полученных рядов наблюдений незначительно отличаются друг от друга и ничто не указывает на наличие систематических погрешностей, то заманчиво объединить все полученные результаты и на основе их математической обработки получить более достоверные сведения об измеряемой величине.
2. Аналогичные измерения были выполнены в разных лабораториях различными методами и получены отличающиеся друг от друга результаты. Естественно и в этом случае, используя все имеющиеся данные, попытаться получить более достоверные значения измеряемых величин.
3. Измерения, относящиеся к образцовым мерам и измерительным приборам, часто повторяются через некоторое время. В конце концов накапливаются ряды наблюдений и возникает необходимость объединить их. Точность рядов наблюдений различна, с одной стороны, из-за того, что для впервые проводимых измерений характерно большее рассеивание результатов, а с другой стороны, из-за того, что с течением времени средства измерения стареют или заменяются новыми.
Во всех описанных ситуациях приходится прибегать к методам обработки результатов неравнорассеянных рядов наблюдений, задача которых в общем случае заключается в нахождении наиболее достоверного значения измеряемой величины и оценки воспроизводимости измерений.
Основой для расчета служат следующие данные:
Если результаты наблюдений во всех рядах распределены нормально, то нормально распределены и все m средних арифметических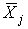 
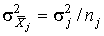
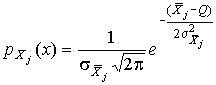
(j=1, 2,…, m) с дисперсиями 
:
,
Q – истинное значение измеряемой величины (при условии, что систематические погрешности исключены).
Для практической обработки результатов неравнорассеянных рядов наблюдений необходимо ввести параметр вес отдельных средних арифметических:
.
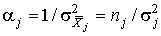
Веса характеризуют степень нашего доверия к соответствующим рядам наблюдений. Чем больше число наблюдений в каждом данном ряду и чем меньше дисперсия результатов наблюдений, тем больше степень доверия к полученному при этом среднему арифметическому и с тем большим весом оно будет учтено при определении оценки истинного значения измеряемой величины
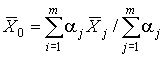 . | (67) |
Иногда удобно пользоваться безразмерными весовыми коэффициентами
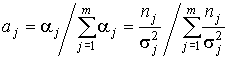 , | (68) |
тогда выражение для среднего взвешенного приобретает простой вид
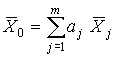 . | (69) |
В соответствии со свойствами оценок максимального правдоподобия дисперсия среднего взвешенного должна равняться единице, деленной на математическое ожидание второй производной от логарифмической функции правдоподобия:
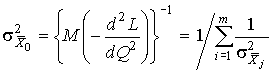 . | (70) |
Отсюда следует, что дисперсия среднего взвешенного меньше дисперсии любого из исходных средних арифметических отдельных рядов наблюдений и поэтому при обработке неравнорассеянных рядов наблюдений точность измерений повышается.
Если теоретические дисперсии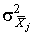 
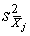
неизвестны, то пользуются их оценками 
, с помощью которых определяют веса или весовые коэффициенты.
При малом числе нормально распределенных результатов наблюдений пользуются распределением Стьюдента с числом степеней свободы
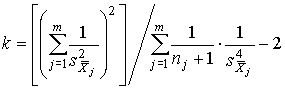 . | (71) |
Если же об исходных распределениях нет никаких заслуживающих внимания данных, то на основании центральной предельной теоремы можно все-таки предполагать, что распределение среднего взвешенного нормально, поскольку оно является суммой большого числа случайных величин с конечными дисперсиями и математическими ожиданиями.
Пример. Тремя коллективами экспериментаторов с помощью различных методов измерения были получены следующие значения ускорения свободного падения (со среднеквадратическими отклонениями результатов измерений):
Весовые коэффициенты отдельных результатов вычислим по формуле (68):
Среднее взвешенное в соответствии с уравнением (69) составляет:
Обработка неравнорассеянных рядов наблюдений
В практике исследовательских работ часто встречаются ситуации, когда необходимо найти наиболее достоверное значение величины и оценить его возможные отклонения от истинного значения на основании измерений, проводимых разными наблюдателями с применением разнообразных измерительных средств и методов измерений в различных лабораториях или условиях внешней среды.
Ряды получающихся при этом результатов наблюдений называются неравнорассеянными, если оценки их дисперсий значительно отличаются друг от друга, а средние арифметические являются оценками одного и того же значения измеряемой величины.
Если средние неравнорассеянных рядов наблюдений мало отличаются друг от друга, то говорят о высокой воспроизводимости измерений, которая количественно характеризуется параметрами рассеивания результатов.
Рассмотрим некоторые случаи, приводящие к необходимости обработки результатов неравнорассеянных измерений:
1. Если при точных измерениях необходимо убедиться в отсутствии неисключенных систематических погрешностей, то измерения проводятся несколькими исследователями или группами исследователей. Если средние арифметические полученных рядов наблюдений незначительно отличаются друг от друга и ничто не указывает на наличие систематических погрешностей, то заманчиво объединить все полученные результаты и на основе их математической обработки получить более достоверные сведения об измеряемой величине.
2. Аналогичные измерения были выполнены в разных лабораториях различными методами и получены отличающиеся друг от друга результаты. Естественно и в этом случае, используя все имеющиеся данные, попытаться получить более достоверные значения измеряемых величин.
3. Измерения, относящиеся к образцовым мерам и измерительным приборам, часто повторяются через некоторое время. В конце концов, накапливаются ряды наблюдений и возникает необходимость объединить их. Точность рядов наблюдений различна, с одной стороны, из-за того, что для впервые проводимых измерений характерно большее рассеивание результатов, а с другой стороны, из-за того, что с течением времени средства измерения стареют или заменяются новыми.
Во всех описанных ситуациях приходится прибегать к методам обработки результатов неравнорассеянных рядов наблюдений, задача которых в общем случае заключается в нахождении наиболее достоверного значения измеряемой величины и оценки воспроизводимости измерений.
Основой для расчета служат следующие данные:
– средние арифметические m рядов равнорассеянных результатов наблюдений постоянной физической величины Q;
– среднеквадратические отклонения (или их оценки) результатов наблюдений в отдельных рядах;
– числа наблюдений в каждом ряду n1,n2,…nm; m – число рядов.
Если результаты наблюдений во всех рядах распределены нормально, то нормально распределены и все m средних арифметических 
с дисперсиями 
:
.
Q – истинное значение измеряемой величины (при условии, что систематические погрешности исключены).
Для практической обработки результатов неравнорассеянных рядов наблюдений необходимо ввести параметр вес отдельных средних арифметических:
.
Веса характеризуют степень нашего доверия к соответствующим рядам наблюдений. Чем больше число наблюдений в каждом данном ряду и чем меньше дисперсия результатов наблюдений, тем больше степень доверия к полученному при этом среднему арифметическому и с тем большим весом оно будет учтено при определении оценки истинного значения измеряемой величины
В соответствии со свойствами оценок максимального правдоподобия дисперсия среднего взвешенного должна равняться единице, деленной на математическое ожидание второй производной от логарифмической функции правдоподобия:
.
Отсюда следует, что дисперсия среднего взвешенного меньше дисперсии любого из исходных средних арифметических отдельных рядов наблюдений и поэтому при обработке неравнорассеянных рядов наблюдений точность измерений повышается.
Если теоретические дисперсии неизвестны, то пользуются их оценками, с помощью которых определяют веса или весовые коэффициенты.
При малом числе нормально распределенных результатов наблюдений пользуются распределением Стьюдента с числом степеней свободы
.
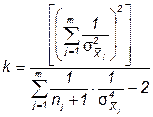
Если же об исходных распределениях нет никаких заслуживающих внимания данных, то на основании центральной предельной теоремы можно все-таки предполагать, что распределение среднего взвешенного нормально, поскольку оно является суммой большого числа случайных величин с конечными дисперсиями и математическими ожиданиями