Что такое нетрадиционная система счисления
Что такое нетрадиционная система счисления
В рассмотренных выше системах счисления «вес» единицы любого разряда, кроме первого, всегда равнялся»весу» единицы предшествующего разряда, умноженному на постоянное основание системы Р. Можно, однако, привести пример такой системы счисления, в которой смысл понятия «основание системы счисления» заметно отличается от традиционного. Предлагаемая система является следствием расширения нашего представления о роли основания системы счисления. Сущность нового подхода легко представить, если рассмотреть счеты необычной конструкции.
Поскольку каждая косточка на второй проволоке заменяет две косточки, расположенные на первой проволоке, то вес этой косточки равен 2. Каждая косточка третьей проволоки заменяет три косточки второй проволоки, и, следовательно, ее вес в 6 = 3·2·1 раз больше веса косточки на первой проволоке. Из этих разъяснений следует, что косточка, расположенная на n-ой проволоке, имеет вес n!. Вес единиц от разряда к разряду растет, но неравномерно. Это приводит к представлению числа в следующем виде:
Получаем, что N-разрядное число, «списанное со счет», оказывается представленным не в виде суммы степеней основания Р, а в виде суммы факториалов n первых натуральных чисел.
Эту систему счисления относят к нетрадиционным позиционным и называют факториальной системой счисления.
С числами этой системы можно выполнять арифметические действия по правилам, незначительно отличающимся от правил десятичной арифметики.
Как и в других системах счисления, в факториальной системе можно рассматривать дробные числа.
Каких-либо существенных практических применений этой системы, основанных на необычной сущности цифрового и многочленного представления, по-видимому, нет. Рассмотрение этой системы прежде всего полезно как методический подход в расширении представлений о системах счисления и обобщении принципа позиционности.
К нетрадиционным системам счисления относят и фибоначчиеву систему счисления.
Алфавитом этой системы счисления являются цифры 0 и 1. В записи числа в фибоначчиевой системе не могут стоять две единицы подряд.
Заметим, что системы, аналогичные фибоначчиевой, применяются при кодировании чисел. Это практически и теоретически интересные системы записи чисел. Изучение особенностей таких систем продолжается и в настоящее время.
Тема 2. Позиционные нетрадиционные системы счисления
Тема 2. Позиционные нетрадиционные системы счисления
К нетрадиционным системам счисления относятся системы, в которых либо базис не является геометрической прогрессией, а символы алфавита есть целые неотрицательные числа (фибоначчиева и факториальная системы счисления), либо базис является геометрической прогрессией, но его символы не являются целыми неотрицательными числами (уравновешенные системы счисления).
1. Переведите числа из D10 в факториальную систему счисления всевозможными вариантами представления:
| 0) 46; 35; | 1) 29; 51; | 2) 22; 47; | 3) 19; 43; | 4) 55; 21; |
| 5) 34; 53; | 6) 57; 30; | 7) 24; 38; | 8) 50; 18; | 9) 25; 46. |
2. Переведите числа из D10 в троичную симметричную систему счисления всевозможными вариантами представления:
| 0) 16; 25; | 1) 19; 35; | 2) 20; 41; | 3)14; 50; | 4) 15; 52; |
| 5) 12; 23; | 6) 17; 60; | 7) 18; 58; | 8) 16; 48; | 9) 13; 49. |
3. Переведите числа из D10 в фибоначчиеву систему счисления всевозможными вариантами представления:
| 0)75; 39; | 1)52; 33; | 2)44; 70; | 3)65; 34; | 4) 45; 81; |
| 4)74; 41; | 5)79; 36; | 6)54; 80; | 7)50; 38; | 9) 55; 26. |
4. Переведите числа из фибоначчиевой системы счисления в D10:
| 0) 11001fib 10100fib 10011fib | 1) 10101 fib 10101fib 11101fib | 2) 10001 fib 10101fib 11011fib | 3) 10100 fib 11011fib 11010fib | 4) 11100 fib 10010fib 11101fib |
| 5) 11011 fib 10101fib 10000fib | 6) 10111 fib 11001fib 11001fib | 7) 11101 fib 10111fib 11101fib | 8) 10110 fib 10001fib 11010fib | 9) 10000 fib 10100fib 11001fib |
5. Переведите числа из факториальной системы счисления в D10:
| 0) 405ф 165ф 102ф | 1) 135ф 657 ф 210ф | 2) 307ф 703 ф 461ф | 3) 383ф 601 ф 226ф | 4) 356ф 230 ф 501ф |
| 5) 255ф 280 ф 370ф | 6) 414ф 303 ф 382ф | 7) 503ф 509 ф 264ф | 8) 610ф 418 ф 305ф | 9) 801ф 380 ф 557ф |
6. Переведите числа из троичной симметричной системы счисления в D10:
Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)
Традиционные и нетрадиционные системы счисления
Для представления цифровых величин используются не только цифры натурального ряда, наиболее широко распространенные для традиционных величин. В XIII веке итальянский математик Леонардо Фибоначчи из Пизы, наблюдая закономерности увеличения численности биологических популяций, открыл интересную числовую последовательность, названную его именем [2].
Действительно, если в отличие от натурального ряда, в котором каждое последующее слагаемое образуется путем увеличения предыдущего элемента на единицу: 0, 1, 2, 3… и т.д., то в ряду Фибоначчи каждый последующий элемент есть сумма двух предыдущих: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 и т.д. Однако более интересное заключается в том, что отношение двух соседних элементов ряда при возрастании их номера до бесконечности имеет предел:

Однако долгое время после открытия числа ряда Фибоначчи рассматривались только как экзотические последовательности и мало использовались при исследованиях и в технике.
В начале 20-х годов прошлого века после появления основополагающих работ Норберта Винера по кибернетике, интерес к системам счисления стал возрастать. Применительно к вычислительной технике это привело к тому, что предпочтение долгое время отдавалось двоичной системе.
В начале 30-х годов 20-го столетия швейцарский исследователь Э. Цекендорф предложил систему счисления на основе чисел Фибоначчи:
|
В формуле (1.2) представлено фактическое определение чисел Фибоначчи. Однако наиболее «революционным» оказалось предложение в 1957г. американским математиком Дж. Бергманом. Им была предложена новая система τ-счисления:
A = anτ n + an-1τ n-1 +…+ aiτ i +…+ a1τ 1 = 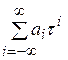
Коды Фибоначчи и «золотой пропорции» можно рассматривать как некоторое обобщенное классическое двоичное счисление. Для представления числа в них используются те же двоичные символы 0 и 1, образующие запись кода. Различие между ними возникает на этапе интерпретации весов разрядов. Например,
2 6 + 2 3 + 2 2 + 2 0 = 45– в двоичном коде;
13 + 3 + 2 + 1 = 19 – в коде Фибоначчи;
τ 6 + τ 3 + τ 2 + τ 0 = А – вещественное число в τ- коде.
Особенностью кодов Фибоначчи является их естественная «избыточность», которая и используется для контроля преобразования информации в компьютерах. Например, число 19 в кодах Фибоначчи имеет и другие представления
= 1010001 = «минимальная» форма
= 0111101 = «максимальная» форма
Как видно из примера различные кодовые последовательности одного и того же числа могут получаться с помощью специальных операций «свертки»- (011→100) и «развертки»-(100→011). В этих операциях две рядом расположенные единицы заменяются нулями и наоборот.
Если над кодовой последовательностью выполнить все возможные свертки, то получится так называемая «минимальная» форма кодового изображения (отсутствие двух рядом стоящих единиц). Если осуществлять все развертки, то получиться «максимальная форма», в которой не встречается рядом двух нулей. Обе формы могут существовать в единственном числе.
Это свойство используется при проектировании так называемых «самопроверяющихся» компьютеров – «компьютеров Фибоначчи». Известно, что компьютеры, использующие двоичную систему счисления, не являются абсолютно надежными. Действительно, вовремя обнаружить перемену места 0 и 1 в 64-разрядном двоичном числе – задача очень трудная. Для нахождения таких ошибок приходится добавлять алгоритмы подсчета контрольных сумм, что сказывается на быстродействии программ в целом.
Другое дело – коды Фибоначчи. Здесь переход 0 в 1 и обратно сразу вызывает необходимость проведения операций свертки и развертки. Поэтому компьютеры Фибоначчи называют еще «самосинхронизующимися» компьютерами.
Существенным свойством системы счисления, особенно с позиций «информационной эпохи», является степень ее пригодности для конструирования вычислительных машин. При этом кроме простоты осуществления арифметических операций важно учитывать то, что называется «экономичностью» системы. Под этим понимается тот запас чисел, которые можно записать в данной системе с помощью определенного количества знаков.
Поясним это на примере. Чтобы в десятичной системе записать 1000 чисел (от 0 до 999), необходимо тридцать знаков (по десять цифр для каждого разряда). А в двоичной системе можно с помощью тридцати знаков записать 

Но какая из систем счисления самая экономичная? Невероятно, но ответить на этот вопрос можно, решив вполне конкретную задачу [3]. Пусть имеется 60 знаков. Можно, разбив их на 30 групп по два элемента в каждой, записать с их помощью в двоичной системе любое число, имеющее не более тридцати двоичных разрядов, т.е. в обще сложности 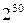
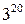

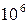
Посмотрим, какая из возможных здесь систем самая экономичная, т.е. позволяет записать с помощью данных 60 знаков наибольшее количество чисел. Иными словами, речь идет о том, какое из чисел:
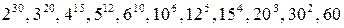
наибольшее. Легко проверить, что наибольшим здесь будет число 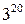
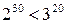
Так как 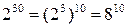
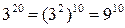
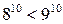
Но в такой форме оно очевидно. Далее:

Следовательно, в силу уже доказанного,
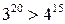
Точно также легко проверить и справедливость следующей цепочки неравенств.
Таким образом, троичная система оказалась самой экономичной. Двоичная и равносильная ей, в смысле экономичности, четверичная система несколько уступают троичной, но превосходят все остальные системы.
Этот вывод никак не связан с тем, что рассматривалось именно шестьдесят знаков. Этот пример приведен только потому, что 60 знаков удобно разбивать на группы по 2, 3, 4, 5, и т.д. знаков.
В общем случае, если взять 
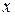
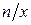

Если рассмотреть это выражение, как функцию переменной х, то можно найти то значение х, при котором эта функция достигает максимум. Несложно показать, что оно равно 

В середине прошлого века в Советском Союзе в МГУ Николаем Петровичем Брусенцовым был построен первый в мире компьютер на троичной системе счисления под названием «Сетунь». Основа его построения – логический элемент с тремя устойчивыми состояниями (0, 1, 2) на магнитных элементах [2].
I.2.3. Статистическая мера информации
При вероятностном подходе информация рассматривается как сообщения об исходе случайных событий, реализации случайных величин и функций, а количество информации ставится в зависимость от априорных вероятностей этих событий, величин, функций. Из опыта известно, что сообщение о часто встречающихся событиях, вероятность появления которых стремиться к 1, то есть к показателю полной достоверности, является малоинформативным. Столь же малоинформативным является сообщение о противоположном событии.
События можно рассматривать как возможные исходы некоторого опыта, причем все исходы составляют ансамбль в виде полной группы событий 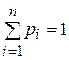
Вообще событиями 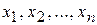
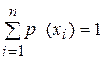
В материальных системах неопределенность каждой ситуации характеризуется энтропией. Понятие энтропии имеет очень широкое толкование и распространяется на многие области знания [1, 9].
Так энтропия в термодинамике означает вероятность теплового состояния вещества, в математике – степень неопределенности ситуации в абстрактной задаче, в информатике она характеризует способность источника отдавать информацию. Однако все эти понятия родственны между собой и в общем случае отображают степень богатства и неожиданности состояния.
В статистической теории информации (теории связи), предложенной К.Шенноном в 1946г., энтропия количественно выражается как средняя функция множества вероятностей каждого из возможных исходов опыта:
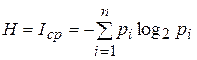
Количество информации только тогда равно энтропии, когда неопределенность ситуации снимается полностью. В общем случае нужно считать, что количество информации есть уменьшение энтропии вследствие опыта. Если неопределенность снимается полностью, то информация равна энтропии: I=H.
В случае неполного разрешения имеет место частная информация, являющаяся разницей между начальной и конечной энтропией: I=H1-H2
Наибольшее количество информации получается тогда, когда полностью снимается неопределенность, причем эта неопределенность была наибольшей – вероятности всех событий были одинакова. Это соответствует максимально возможному количеству информации, оцениваемому мерой Хартли 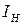
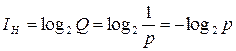
Q – число событий, p – вероятность их реализации в условиях равноопределенности. Таким образом 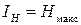
Абсолютная избыточность информации Dабс представляет собой разность между максимально возможным количеством информации и энтропией: Dабс = 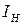
Непозиционные системы счисления
Здравствуйте, на этой странице рассмотрим одну из важных тем в информатике – а именно непозиционные системы счисления. Здесь вы узнаете, что является непозиционными системами, и познакомитесь с основными определениями, которые относятся к этой теме. Также затронем их отличия от позиционных нумераций и приведем достоинства и недостатки.
Определение непозиционной системы счисления
Непозиционными являются нумерации, где положение цифры в числе (разряд) не влияет на её значение.
Чтобы разобраться конкретно в том, что здесь написано, выберем самое популярное исчисление, которое называется десятичным. Вы все с ним знакомы. Им пользуются люди в большинстве стран мира. Алфавит десятичной нумерации состоит из арабских знаков – чисел от 0 до 9. Данный вид записи является позиционным. Почему, спросите вы? Всё просто. В качестве примера приведем два числа – 1000 и 10. Смотрите на цифру один – в зависимости от того, какое место она занимает в числе, меняется значение, которое она обозначает. В числе 1000 – тысячи, а 10 – десятки.
В непозиционных представлениях все обстоит совсем иначе. Давайте приведем в пример Римскую нотацию. Её вы тоже видели и с ней знакомы. Вспомните – в книгах по истории с помощью неё представляются века и номера монархов. Как пример, Петр I или Иван IV Грозный. Обратите внимание на I и IV, которые в арабском виде запишутся как 1 и 4. Здесь значение единицы не изменяется от того, какое место она занимает. На первом месте она стоит или на втором – неважно.
Историками считается, что исчисления, которые называются непозиционными, ведут свои корни от глубокой древности – это первые формы для счета, которые использовал человек. Поговорим дальше про их виды и разберем недостатки.
Примеры непозиционных систем счисления
Унарная непозиционная
Еще называется непозиционной единичной. Скорее всего, вы уже догадались, почему она так называется. Дело в том, что в этой форме записи используется только один знак. Это представление применяли древнейшие люди. Для записи значений использовались насечки на костях животных или стенах пещеры. Также в обиходе были зарубки на дереве. Используется до сих пор. Вспомните сериалы, где заключенные отсчитывают свои дни в неволе. Также применяется для обучения детей счету – так называемый пальцевый метод.
Унарная сс – отметки на кости
Римская непозиционная
Её мы уже привели выше. Используется до сих пор. В качестве алфавита здесь применяются латинские буквы, такие как V, I, D, M, C, X, L. Всё остальное же получается с помощью различного написания этих символов – здесь используются принципы вычитания и сложения. Так если младший разряд записывается перед старшим, то он вычитается. Если же наоборот, то складывается. Есть у неё и еще одна особенность – нет 0, который является отсутствием числа. Ниже приведена небольшая табличка с расшифровкой римских цифр.
Римское непозиционное счисление появилось в Риме на самом пике процветания империи. Однако и после того как империя распалась этим счислением пользовались еще очень долго. Она использовалась в Европе до 1200х годов, пока великий математик Леонардо Фибоначчи не издал трактат – “Книга Абака”. В нем ученый показывал превосходство позиционных систем над непозиционными.
Египетская непозиционная
Возникла в третьем тысячелетии до нашей эры. Все значения записывались здесь с помощью иероглифов. Каких-то особых правил здесь не существовало – все числовые значения просто складывались. Также не было и правил, которые относятся к записи – последовательность могла быть записана, как слева на право, так и справа налево. Иероглифы могли занимать любой разряд. Ниже приведена табличка со значениями некоторых из них.
Алфавитные системы счисления
Стоит отметить эти формы записи. Здесь все очень просто – каждой букве алфавита сопоставлялась цифра. Стоит отметить, что эти непозиционные системы являются более совершенными, чем все предыдущие, поскольку имелись обозначения десятков и сотен. К недостаткам можно отнести их сложность. Здесь можно выбрать два популярных примера.
Славянская
Использовалась нашими предками во времена древней Руси. Первые записи о ней в летописи временных лет появляются с начала десятого века. Каждой букве глаголицы соответствовало некоторое число. Полностью вышла из использования во времена Российской Империи в восемнадцатом веке, её место заняло десятичное исчисление. Пользуемся мы им, и посей день.
Греческая
Она же называется непозиционной новогреческой или ионийской. Упоминания о ней датируются третьим веком до нашей эры. Здесь счет велся буквами, которые употреблялись в римской письменности. Пришла на смену старогреческому формату. По сути, непозиционное кириллическое представление является её копией.
Достоинства и недостатки. Возможность использования в информатике и других науках.
К достоинствам можно отнести только их простоту. Как мы уже говорили выше, та же унарная непозиционная система применяется для обучения детей. Однако недостатков у них гораздо больше и они очень существенные:
Всё эти недостатки делают их использование в математике и информатике непрактичным.
Заключение
В качестве итогов можно сказать, что после прочтения этого материала вы имеете полное представление о том, что называется непозиционными системами счисления, овладели нужным определением. Знаете виды, которые использовали разные народы в различных частях земного шара. Теперь вы имеете представление о том, как считали люди в Риме, Египте, Греции и древней Руси. Знаете их плюсы и минусы. Понимаете, почему нельзя использовать их в информатике. Как по мне тема достаточно легкая, но очень интересная. При возникновении вопросов задайте их в комментариях к этой записи. Буду рад на них ответить. Также вы можете почитать другие материалы, которые затрагивают информатику на нашем сайте.