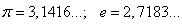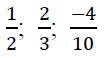Что такое нецелое число в математике пример
Математика
Тестирование онлайн
Натуральные числа
Это числа, которые используются при счете: 1, 2, 3. и т.д.
Ноль не является натуральным.
Натуральные числа принято обозначать символом N.
Целые числа. Положительные и отрицательные числа
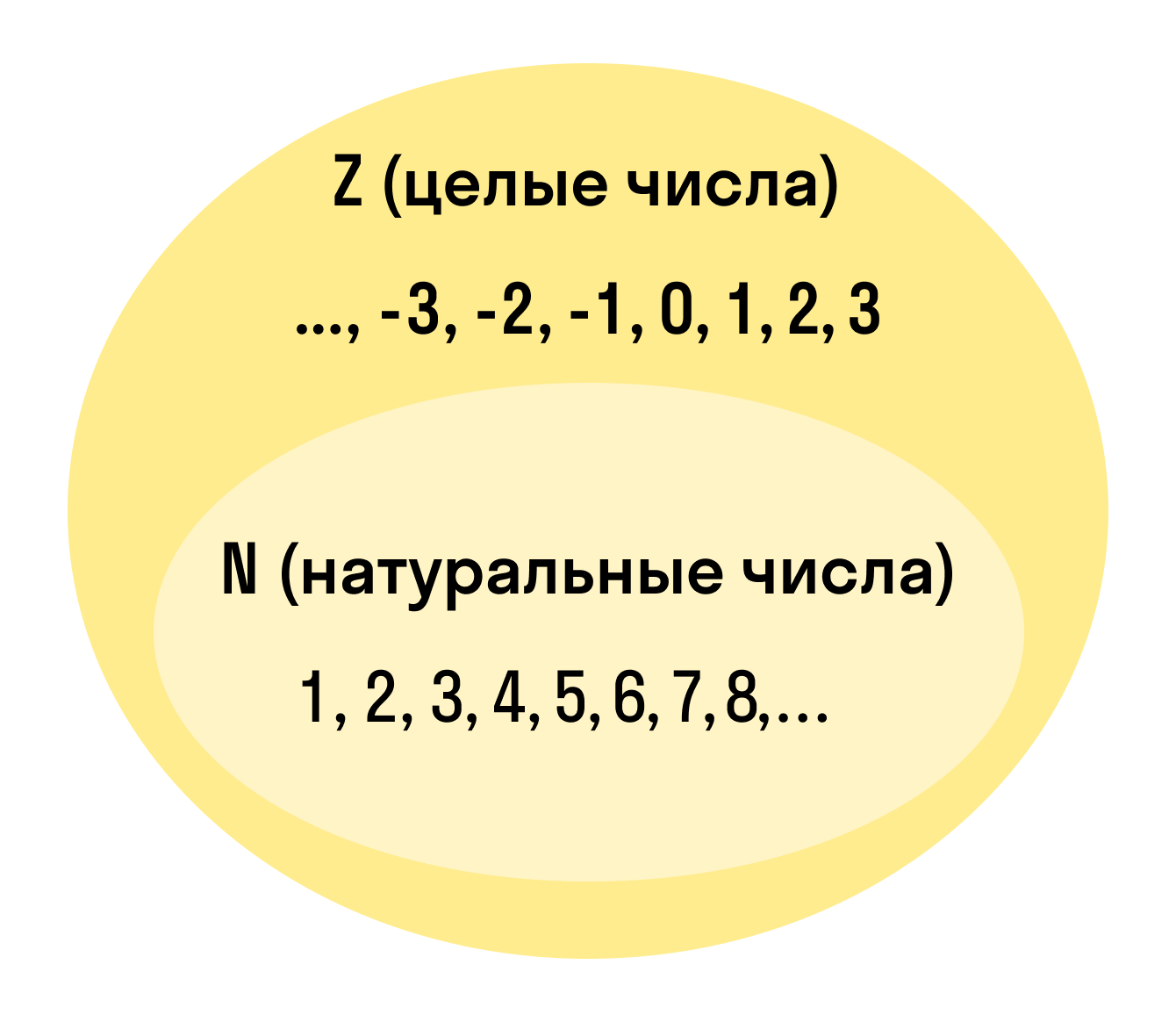
Натуральные числа, противоположные им и ноль называют целыми числами. Множество целых чисел обозначают символом Z.
Рациональные числа
Множество рациональных чисел обозначается Q. Все целые числа являются рациональными.
Иррациональные числа
Бесконечная непериодическая дробь называется иррациональным числом. Например:
Множество иррациональных чисел обозначается J.
Действительные числа
Множество всех рациональных и всех иррациональных чисел называется множеством действительных (вещественных) чисел.
Действительные числа обозначаются символом R.
Округление чисел
Округлить 8,759123. с точностью до целой части.
Округлить 8,759123. с точностью до десятой части.
Округлить 8,759123. с точностью до сотой части.
Округлить 8,759123. с точностью до тысячной части.
Какие числа называются целыми
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение целых чисел
Что важно знать о целых числах:
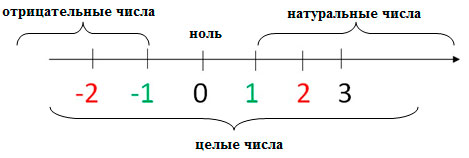
Целые числа на числовой оси выглядят так:
На координатной прямой начало отсчета всегда начинается с точки 0. Слева находятся все отрицательные целые числа, справа — положительные. Каждой точке соответствует единственное целое число.
В любую точку прямой, координатой которой является целое число, можно попасть, если отложить от начала координат данное количество единичных отрезков.
Натуральные числа — это целые, положительные числа, которые мы используем для подсчета. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 + ∞.
Целые числа — это расширенное множество натуральных чисел, которое можно получить, если добавить к ним нуль и отрицательные числа. Множество целых чисел обозначают Z.
Выглядит эти ребята вот так:
Последовательность целых чисел можно записать так:
Свойства целых чисел
Таблица содержит основные свойства сложения и умножения для любых целых a, b и c:
Числа: натуральные, целые, рациональные, иррациональные, действительные
Натуральные числа
Натуральные числа определение – это целые положительные числа. Натуральные числа используют для счета предметов и многих иных целей. Вот эти числа:
Это натуральный ряд чисел.
Ноль натуральное число? Нет, ноль не является натуральным числом.
Сколько натуральных чисел существует? Существует бесконечное множество натуральных чисел.
Каково наименьшее натуральное число? Единица — это наименьшее натуральное число.
Каково наибольшее натуральное число? Его невозможно указать, ведь существует бесконечное множество натуральных чисел.
Сумма натуральных чисел есть натуральное число. Итак, сложение натуральных чисел a и b:
с — это всегда натуральное число.
Произведение натуральных чисел есть натуральное число. Итак, произведение натуральных чисел a и b:
с — это всегда натуральное число.
Разность натуральных чисел Не всегда есть натуральное число. Если уменьшаемое больше вычитаемого, то разность натуральных чисел есть натуральное число, иначе — нет.
Частное натуральных чисел Не всегда есть натуральное число. Если для натуральных чисел a и b
где с — натуральное число, то это значит, что a делится на b нацело. В этом примере a — делимое, b — делитель, c — частное.
Делитель натурального числа — это натуральное число, на которое первое число делится нацело.
Каждое натуральное число делится на единицу и на себя.
Простые натуральные числа делятся только на единицу и на себя. Здесь имеется ввиду делятся нацело. Пример, числа 2; 3; 5; 7 делятся только на единицу и на себя. Это простые натуральные числа.
Единицу не считают простым числом.
Числа, которые больше единицы и которые не являются простыми, называют составными. Примеры составных чисел:
Единицу не считают составным числом.
Множество натуральных чисел составляют единица, простые числа и составные числа.
Множество натуральных чисел обозначается латинской буквой N.
Свойства сложения и умножения натуральных чисел:
переместительное свойство сложения
сочетательное свойство сложения
переместительное свойство умножения
сочетательное свойство умножения
распределительное свойство умножения
Целые числа
Целые числа — это натуральные числа, ноль и числа, противоположные натуральным.
Числа, противоположные натуральным — это целые отрицательные числа, например:
Множество целых чисел обозначается латинской буквой Z.
Рациональные числа
Рациональные числа — это целые числа и дроби.
Любое рациональное число может быть представлено в виде периодической дроби. Примеры:
Из примеров видно, что любое целое число есть периодическая дробь с периодом ноль.
Любое рациональное число может быть представлено в виде дроби m/n, где m целое число,n натуральное число. Представим в виде такой дроби число 3,(6) из предыдущего примера:
Другой пример: рациональное число 9 может быть представлено в виде простой дроби как 18/2 или как 36/4.
Множество рациональных чисел обозначается латинской буквой Q.
Подробнее о рациональных числах в разделе Рациональные числа.
Иррациональные числа
Иррациональные числа — это бесконечные непериодические десятичные дроби. Примеры:
Подробнее об иррациональных числах в разделе Иррациональные числа.
Действительные числа
Действительные числа – это все рациональные и все иррациональные числа.
Множество действительных чисел обозначается латинской буквой R.
Виды чисел.
У нас есть числа натуральные, целые, рациональные и иррациональные, а также вещественные или действительные и еще есть другие, но в школьной программе в основном используют эти числа.
Натуральные числа ( N ) − это числа, используемые для счета предметов. Нуль не является натуральным числом.
Например: 1; 2; 3; 132; 168; 326; 548; 10050…
Целые числа ( Z ) — множество чисел, получающееся в результате арифметических операций сложения (+) и вычитания (−) натуральных чисел.
Например: …−3; −2; 1; 0; 548; 10050…
Рациональные числа ( Q ) – это положительные и отрицательные числа можно представить в виде обыкновенной несократимой дроби вида: 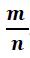
где m−целое число (числитель), n – натуральное число (знаменатель).
Например:
Иррациональные числа ( I ) − числа, которые не представимыми в виде дроби вида 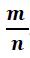
Например: √2; √5; π; e
Вещественные (действительные) числа ( R ).
Рациональные числа и иррациональные числа образуют множество действительных чисел.
Изобразим это множество чисел в виде рисунка:
Видно их вложенность друг в друга.
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
Что такое целые числа
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы поговорим о ЦЕЛЫХ ЧИСЛАХ.
Это весьма обширное понятие из математики, с которым школьники сталкиваются уже в 5 классе.
Целые числа — это.
Целые числа – это все положительные, все отрицательные числа и ноль. Главное, чтобы они не содержали дробной части.
Согласно этому определению, к целым числам можно отнести:
и так далее. Ведь у них нет дробной части. А вот числа:
и так далее не могут считаться целыми, так как у них есть какие-то цифры после запятой или они являются дробью.
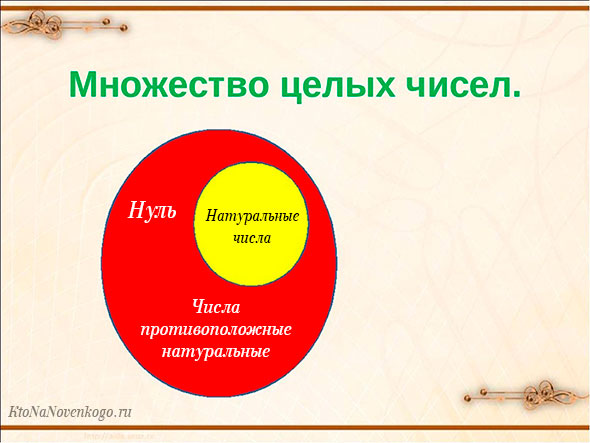
Все многообразие целых чисел называется множеством целых чисел. Это официальный математический термин. И обозначается он буквой Z.
В это множество входят и так называемые натуральные числа (это что?). Это все те, которые имеют положительное значение, но опять же без дробной части. Проще говоря, все числа, которые мы используем при счете. Например, 1, 2, 5, 10, 100 и так далее.
Множество натуральных чисел обознается буквой N. И зависимость его и множества целых чисел наглядно показана на следующем рисунке.
Отсюда можно сделать важный вывод:
Любое натуральное число автоматически является еще и целым. Но при этом далеко не каждое целое число является еще и натуральным.
А можно представить это и в таком варианте. Целые числа — это:
Каким бы определением вы не пользовались, главное, чтобы было все понятно.
История изучения целых чисел
Опять же эту историю нужно разделить на три части. Ведь изучение натуральных чисел, а также открытие нуля и отрицательных чисел происходило независимо друг от друга. Да еще и в разных странах.
Изучение натуральных чисел
Тут все максимально просто. Эти числа возникли, как только человеку понадобилось считать – будь то куски мяса или количество бревен для дома.
Более точное изучение натуральных чисел начинается в Древнем Египте и Древней Месопотамии, а это более 6 тысяч лет назад.
А современные математики опираются на то, что после себя оставил древнегреческий ученый Пифагор. Он как раз активно собирал египетские и вавилонские данные, а после отразил их в своих трудах.
Открытие нуля
Конечно, египтяне, вавилоняне и даже греки знали о существовании нуля. Но не считали его числом, а потому не пользовались им. Это, кстати, приносило им немало сложностей. Они порой часами решали задачки, которые нынешний школьник посчитает за минуту.
Но официально число ноль появилось в 5-м веке. И «изобрели» его в Индии. Дело в том, что у местных жителей всегда существовало убеждение, что «ничто – это тоже что-то». Даже понятие Нирвана, которое обозначает состояние небытие, зародилось именно в Индии.
Потому-то там и придумали символ, который обозначал бы «ничто». Авторами его стали математики Брахмагупта и Ариабхата.
Как видите, индийский символ нуля очень похож на современный. Ну, разве что приплюснут и больше напоминает правильную окружность. Форма выбрана не случайно. По индийским поверьям, ноль символизирует круговорот жизни и мироздания. Его еще называют «змея вечности».
Когда арабы завоевали часть Индии, они переняли все математические знания. А во время крестовых походов многое, в том числе и цифры, перекочевали в Европу. Хотя потребовалось еще несколько сотен лет, чтобы «ноль» стал неотъемлемой частью европейской науки.
Открытие отрицательных чисел
Отрицательные числа первыми начали изучать китайцы во 2 веке до нашей эры. Их использовали в торговле и называли «долгами». А обычные числа – «имуществом». А для записи отрицательных чисел использовали перевернутый вид.
А вот в Европе к ним очень долго относились пренебрежительно, считая «несуществующими» и «абсурдными». Лишь в 12 веке математик Леонардо Фибоначчи (автор знаменитого числового ряда) описал их в своей книге «Книга Абака».
В середине 16 века математик Михаил Штифель посвятил им целый раздел в своей книге «Полная арифметика».
Но признание они получили лишь в 17 веке, после того как известный Рене Декарт создал свою систему координат.
В ней он также использовал нуль, привязав к нему положительные и отрицательные числа. Одни находились справа от него, а другие – слева.
Свойства целых чисел
Всем целым числам свойственны следующие характеристики:
Если А и В – целые, то А+В=целое, А-В=целое и А*В=целое
А + В = В + А, А * В = В * А
Добавим: точно такое же правило действует и при делении. Минус на минус дают плюс. А минус на плюс или плюс на минус всегда дают минус.
Вместо заключения
Мы уже рассказали, с каким трудом в нашу жизнь попали отрицательные числа. Но сегодня они широко используются не только в математике.
Ну и, наконец, слова положительный и отрицательный используются и в более разговорном смысле, как синонимы хорошего и плохого.
Например, в книгах и фильмах обязательно есть положительные и отрицательные герои. Также и наши черты характера, эмоции и поступки можно разделить на эти две категории.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (1)
Сами по себе числа ничего не значат, будь они даже целыми и натуральными, чтобы в них был смысл, они должны иметь привязку к чему-либо. Например, единица меньше пятидесяти, но всегда ли единица меньше? Если я скажу, что один рубль меньше пятидесяти копеек, то это будет ложью.