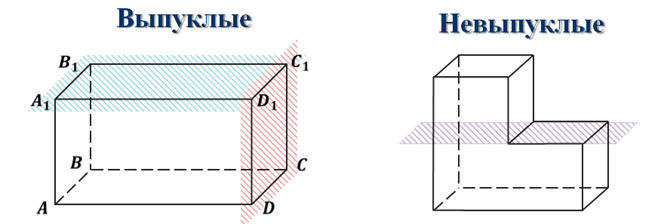
Что такое невыпуклый многогранник

Лекция по математике на тему «Многогранники»

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Понятие многогранника. Виды многогранников.

Выпуклые и невыпуклые, правильные и неправильные

Преподаватель: Горячева А.О.

Многогранником называется ограниченное тело, поверхность которого состоит из конечного числа многоугольников.

Выпуклые и невыпуклые многогранники.

Правильные (Платоновы тела) и неправильные многогранники.

Если данное утверждение не выполняется, многогранник будет являться невыпуклым (рис. 2б).

«Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук» (Л.Кэрролл).

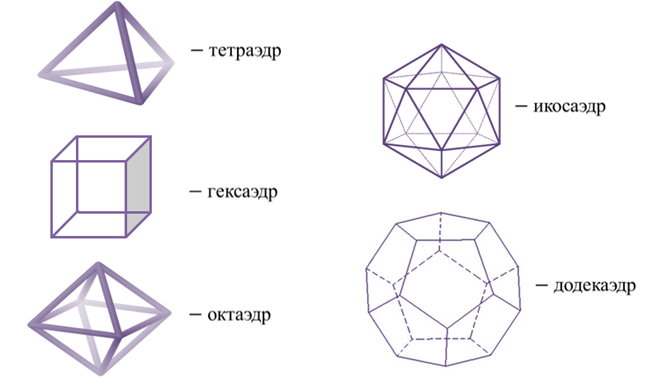
Всего существует пять правильных многогранников (рис. 3).

Если посчитать количество граней, ребер и вершин указанных многогранников, получим (таб. 1):

Тип правильного многогранника

Число сторон у грани

Число рёбер, примыкающих к вершине

Общее число вершин

Общее число граней

Первые упоминания о многогранниках известны еще за три тысячи лет до нашей эры в Египте и Вавилоне. Достаточно вспомнить знаменитые египетские пирамиды и самую известную из них – пирамиду Хеопса. Это правильная пирамида, в основании которой квадрат со стороной 233 м и высота которой достигает 146,5 м. Не случайно говорят, что пирамида Хеопса – немой трактат по геометрии.

История правильных многогранников уходит в глубокую древность. Начиная с 7 века до нашей эры в Древней Греции создавались философские школы. Большое значение в этих школах приобрели рассуждения, с помощью которых удалось получить новые геометрические свойства.

Пифагорейцы полагали, что материя состоит из четырех основных элементов: огня, земли, воздуха и воды. Существование пяти правильных многогранников они относили к строению материи и Вселенной. Согласно этому мнению, атомы основных элементов должны иметь форму различных тел: Вселенная – додекаэдр, Земля – куб, Огонь – тетраэдр, Вода – икосаэдр,

Полуправильным многогранником называется выпуклый многогранник, гранями которого являются правильные многоугольники (возможно, и с разным числом сторон) и все многогранные углы равны.

Существует тринадцать полуправильных многогранников, которые носят название Архимедовых тел: усеченный тетраэдр (рис. 4а), усеченный октаэдр (рис. 4б), усеченный икосаэдр (рис. 4в), усеченный куб (рис. 4г), усеченный додекаэдр (рис. 4д), кубооктаэдр (рис. 4е), икосододекаэдр (рис. 4ж), усеченный кубооктаэдр (рис. 4з), усеченный икосододекаэдр (рис. 4и), ромбокубооктаэдр (рис. 4к), ромбоикосододекаэдр (рис. 4л), плосконосый куб (рис. 4м), плосконосый додекаэдр (рис. 4н), призма (рис. 4о) и антипризма (рис. 4п). Антипризма – это многогранник, у которого две параллельные грани (основания) — равные между собой правильные n-угольники, а остальные 2n граней (боковые грани) — правильные треугольники.

Тетраэдр и гексаэдр (куб) не имеют звёздчатых форм, так как их грани при продлении через рёбра более не пересекаются.

Додекаэдр имеет 3 звёздчатые формы: малый звёздчатый додекаэдр (рис. 5а), большой додекаэдр (рис. 5б), большой звёздчатый додекаэдр (рис. 5в). Первые две из них были открыты И. Кеплером в 1619 году, а третью почти 200 лет спустя построил французский математик и механик Л. Пуансо (1809г). Именно поэтому правильные звездчатые многогранники называются телами Кеплера-Пуансо.

Икосаэдр имеет 59 звёздчатых форм. Одна из этих звёздчатых форм, называемая большим икосаэдром (рис. 6), является одним из четырёх правильных звёздчатых многогранников Кеплера—Пуансо. Его гранями являются правильные треугольники, которые сходятся в каждой вершине по пять; это свойство является у большого икосаэдра общим с икосаэдром.

В работе «О многоугольниках и многогранниках» (1810) Пуансо описал четыре правильных звездчатых многогранника, но вопрос о существовании других таких многогранников оставался открытым. Ответ на него был дан год спустя, в 1811 году, французским математиком О. Коши (1789-1857). В работе «Исследование о многогранниках» он доказал, что других правильных звездчатых многогранников не существует.

Кроме правильных звездчатых многогранников существуют и другие звездчатые формы, получающиеся продолжением граней правильных и полуправильных многогранников.

На рисунке 7 изображен многогранник, называемый звездчатым октаэдром.

Продолжения граней кубооктаэдра приводят к четырем звездчатым многогранникам. Первый из них (рис. 8а) получается достраиванием на гранях кубооктаэдра пирамид и представляет собой соединение куба и октаэдра.

Следующая звездчатая форма кубооктаэдра представлена на рисунке 8б. Она образована из соединения куба и октаэдра добавлением 24 бипирамид.

Третья звездчатая форма кубооктаэдра (рис. 8в) представляет собой соединение шести четырехугольных пирамид, основаниями которых служат квадраты.

Последняя звездчатая форма кубооктаэдра (рис. 8г) является соединением звезды Кеплера и трех правильных четырехугольных призм, общей частью которых служит исходный куб.

Икосододекаэдр имеет 19 звездчатых форм, некоторые из которых представлены на рисунке 9.

Источник

Что такое многогранник? Примеры

Примеры многогранников:

1) каждая сторона одного является одновременно стороной другого (но только одного), называемого смежным с первым (по этой стороне);

Многогранник называется выпуклым, если он лежит по одну сторону от плоскости любой его грани.

Из этого определения следует, что все грани выпуклого многогранника являются плоскими многоугольниками. Поверхность выпуклого многогранника состоит из граней, которые лежат в разных плоскостях. При этом ребрами многогранника являются стороны многоугольников, вершинами многогранника – вершины граней, плоскими углами многогранника – углы многоугольников – граней.

Выпуклый многогранник, все вершины которого лежат в двух параллельных плоскостях, называется призматоидом. Призма, пирамида и усеченная пирамида – частные случаи призматоида. Все боковые грани призматоида являются треугольниками или четырехугольниками, причем четырехугольные грани – это трапеции или параллелограммы.

Популярное

Ключевым элементом этого проекта является правильная треугольная призма.

Монумент «Звезда Кеплера» (норв. Keplerstjernen), высотой 45 метров, расположен недалеко от города Осло (Норвегия) в окрестностях аэропорта.

Нечасто удается встретить многогранники за пределами учебников математики. И если такие геометрические формы как куб, призма и цилиндр встречаются повседневно, то.

Статья в журнале «Наука и Жизнь» рассказывает о достаточно необычном способе построения многогранников.

В выпуске 25 «Волшебных граней» мы обратили взор читателя на то, что разрезая куб плоскостью, мы получаем в точке разреза сечение, имеющее форму.

В этой статье мы познакомим вас с технологиями изготовления геометрических тел из металла, которые применяет мастер Иван Кочкин.

Нам нужны еще фонарики Джека в форме тыквы. Кто же нам поможет? Может быть Архимед?

Источник

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Урок № 13. Многогранники

Перечень вопросов, рассматриваемых в теме:

Многогранник – геометрическое тело, ограниченное конечным числом плоских многоугольников.

Грани многогранника – многоугольники, ограничивающие многогранники.

Ребра многогранника – стороны граней многогранника.

Вершины многогранника – концы ребер многогранника (вершины граней многогранника).

Диагональ многогранника – отрезок, соединяющий две вершины, не принадлежащие одной грани.

Выпуклый многогранник – многогранник, расположенный по одну сторону от плоскости его любой грани.

Невыпуклый многогранник – многогранник, у которого найдется по крайней мере одна грань такая, что плоскость, проведенная через эту грань, делит данный многогранник на две или более частей.

Атанасян Л. С., В. Ф. Бутузов, С. Б. Кадомцев и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы: учеб. Для общеобразоват. организаций: базовый и углубл. уровния. – М.: Просвещение, 2014. – 255 с. (стр. 58, стр. 60 – 61)

Долбилин Н. П. Жемчужины теории многогранников М. : – МЦНМО, 2000. – 40 с.: ил. (стр. 27 – 31)

Открытые электронные ресурсы:

Долбилин Н. П. Три теоремы о выпуклых многогранниках. Журнал Квант.

Теоретический материал для самостоятельного изучения

К определению понятия многогранника существует два подхода. Проведем аналогию с понятием многоугольника. Напомним, что в планиметрии под многоугольником мы понимали замкнутую линию без самопересечений, составленную из отрезков (рис. 1а). Также многоугольник можно рассматривать как часть плоскости, ограниченную этой линией, включая ее саму (рис. 1б). При изучении тел в пространстве мы будем пользоваться вторым толкованием понятия многоугольник. Так, любой многоугольник в пространстве есть плоская поверхность.

Б)

Рисунок 1 – разные подходы к определению многоугольника

Вторая трактовка понятия определяет многогранник как геометрическое тело, ограниченное конечным числом плоских многоугольников.

В дальнейшем, мы будем использовать вторую трактовку понятия многогранника.

Уже известные вам тетраэдр и параллелепипед являются многогранниками. Потому что они являются геометрическими телами, ограниченные конечным числом плоских многоугольников. Еще один пример многогранника — октаэдр (рис. 2)

Рисунок 2 – изображение октаэдра

Многоугольники, ограничивающие многогранник, называются его гранями. Так, у тетраэдра и октаэдра гранями являются треугольники. У тетраэдра 4 грани, отсюда и его название от греч. τετρά-εδρον — четырёхгранник. У октаэдра 8 граней, а от греческого οκτάεδρον от οκτώ «восемь» + έδρα «основание».

Стороны граней называются ребрами, а концы ребер — вершинами многогранника. Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника.

Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани. В остальных случаях многогранник называется невыпуклым (рис.3).

Рисунок 3 – Виды многогранников

Сумма плоских углов при вершине выпуклого многогранника

Рисунок 4 – сумма плоских углов пи вершине многогранника

Теорема Эйлера. Пусть В — число вершин выпуклого многогранника, Р — число его ребер, а Г — число его граней. Тогда верно равенство В – Р+Г= 2.

Теорема Эйлера играет огромную роль в математике. С ее помощью было доказано огромное количество теорем. Находясь в центре постоянного внимания со стороны математиков, теорема Эйлера получила далеко идущие обобщения. Более того, эта теорема открыла новую главу в математике, которая называется топологией.

Примеры и разбор решения заданий тренировочного модуля

Задание 1. Какие из перечисленных объектов НЕ могут быть элементами многогранника? Укажите номера в порядке возрастания.

Элементы многогранника, которые мы выделили: ребра, грани, вершины и диагонали. Ребро и диагональ многогранника – это отрезок. Грань многогранника – многоугольник, или иначе ограниченная часть плоскости. Вершины представляют собой точки. Таким образом, элементами многогранника не могут быть плоскость, луч, многогранник, прямая.

Задание 2. Сопоставьте геометрическим фигурам их вид

Б) пространственная фигура

Вспомним, что изобразить пространственную фигуру можно разными способами. Например, с помощью теней или изображением невидимых линий пунктиром. Так, среди всех изображений плоской фигурой является фигура под номером 1.

Многогранник – геометрическое тело, ограниченное конечным числом плоских многоугольников. Только на изображении 2 фигура ограничена многоугольниками. Таким образом, получаем следующий ответ: 1-А, 2-В, 3-Б

Источник

Понятие многогранника

Урок 25. Геометрия 10 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Понятие многогранника»

Начиная изучать стереометрию, мы говорили, что все геометрические тела делятся на два больших класса тела вращения и многогранники, с некоторыми многогранниками мы с вами уже знакомы. Напомним, какие фигуры мы назвали тетраэдром и параллелепипедом. Мы уже с вами познакомились со свойствами этих фигур.

Сегодняшний наш урок открывает раздел, в котором мы познакомимся с другими многогранниками, но прежде давайте вспомним основные понятия, связанные с многогранниками.

Многогранник представляет собой геометрическое тело, ограниченное конечным числом плоских многоугольников, любые два смежные из которых не лежат в одной плоскости.

Многогранник – это поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело.

Это тело также называется многогранником.

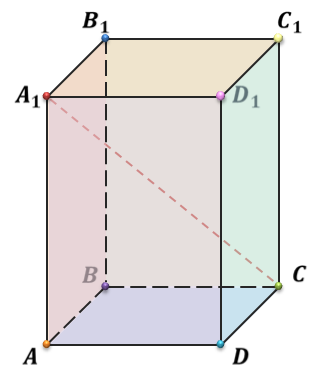
Обратим внимание, из чего состоит поверхность многогранника. Давайте рассмотрим, например, прямоугольный параллелепипед ABCDA₁B₁C₁D₁.

Как уже говорилось ранее, поверхность прямоугольного параллелепипеда состоит из шести прямоугольников. Т.е. его поверхность составлена из шести многоугольников. Назовем их: ABCD, A₁B₁C₁D₁, AA₁B₁B, DD₁C₁C, AA₁D₁D и BB₁C₁C. Многоугольники, из которых составлен многогранник, называют его гранями. Заметим, что никакие две соседние грани многогранника не лежат в одной плоскости.

Отрезок, соединяющий две вершины, не принадлежащие одной грани, например, A₁C – называется диагональю многогранника. В данном случае, диагональ прямоугольного параллелепипеда.

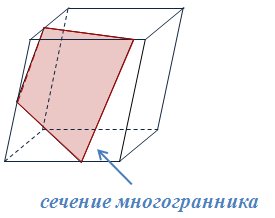
Плоскость, по обе стороны от которой имеются точки многогранника, называется секущей плоскостью, а общая часть многогранника и секущей плоскости – сечением многогранника.

Многогранники, также как и многоугольники бывают выпуклыми и невыпуклыми.

Так, если провести плоскость, например, через грань DD₁C₁C, то весь многогранник будет лежать по одну сторону от этой плоскости. Аналогично, если провести плоскости и через остальные его грани, многогранник всегда будет расположен по одну сторону от этих плоскостей. Такой многогранник называется выпуклым.

Определение. Многогранник называется выпуклым, если он лежит по одну сторону от плоскости каждой своей грани.

Если это условие не выполняется, т.е. многогранник лежит по разные стороны хотя бы от одной плоскости, проходящей через грань, то многогранник называется невыпуклым.

Легко заметить, что все грани выпуклого многогранника являются выпуклыми многоугольниками. Отметим, что в выпуклом многограннике сумма всех плоских углов при каждой его вершине меньше 360°.

Пояснить это утверждение нетрудно. Возьмем многогранник и разрежем его вдоль ребер и все его грани с общей вершиной А развернуты так, что они оказались расположенными в одной плоскости α. Очевидно, что сумма всех плоских улов при вершине А меньше 360°.

А теперь давайте немного окунемся в историю.

Огромный вклад в развитии математики в целом и геометрии в частности внесли философские школы, в которых происходит постепенный переход от практической к теоретической геометрии.

Одной из самых первых и самых известных геометрических школ была пифагорейская, она существовала в VI-V вв. до нашей эры. Названа она была в честь своего основателя древнегреческого ученого Пифагора.

Пифагорейцы использовали правильные многогранники для философских теорий. Так огню они придавали форму тетраэдра (пирамиды), земле – форму гексаэдра (куба), воздуху – форму октаэдра (фигуры, которая образована восьмью равносторонними треугольниками), воде – форму икосаэдра (фигуры, которая образована двадцатью равносторонними треугольниками). По их мнению вся вселенная имеет форму додекаэдра (фигуры, которая состоит из двенадцати правильных пятиугольников).

Но математикой в целом и геометрией в частности интересовались не только ученые. Существует так называемое математическое искусство Эшера.

Голландский художник Мориц Корнилис Эшер, родившийся в 1898 году в Леувардене создал уникальные и очаровательные работы, в которых использованы или показаны широкий круг математических идей.

Правильные геометрические тела — многогранники — имели особое очарование для Эшера. Во многих его работах многогранники являются главной фигурой и в еще большем количестве работ они встречаются в качестве вспомогательных элементов.

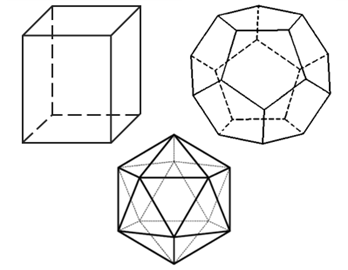
Существует лишь пять правильных многогранников, то есть таких тел, все грани которых состоят из одинаковых правильных многоугольников. Они еще называются телами Платона. Это — тетраэдр, гранями которого являются четыре правильных треугольника, куб с шестью квадратными гранями, октаэдр, имеющий восемь треугольных граней, додекаэдр, гранями которого являются двенадцать правильных пятиугольников, и икосаэдр с двадцатью треугольными гранями. На гравюре «Четыре тела» Эшер изобразил пересечение основных правильных многогранников, расположенных на одной оси симметрии, кроме этого многогранники выглядят полупрозрачными, и сквозь любой из них можно увидеть остальные.

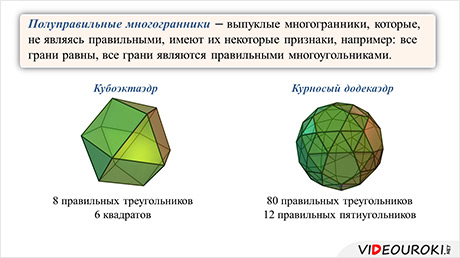
Помимо правильных многогранников существуют так называемые полуправильные многогранники. Это выпуклые многогранники, которые, не являясь правильными, имеют их некоторые признаки, например: все грани равны, все грани являются правильными многоугольниками. К таким фигурам относятся например кубоэктаэдр – фигура, гранями которой являются восемь правильных треугольников и шесть квадратов, или, например, курносый додекаэдр – фигура, которая состоит из восьмидесяти правильных треугольников и двенадцати правильных пятиугольников. Подобных многогранников существует двадцать шесть.

Закончить наш сегодняшний урок хочется словами советского математика Лазаря Ароновича Люстерника «Теория многогранников, в частности выпуклых многогранников,— одна из самых увлекательных глав геометрии».

Источник

Что такое невыпуклый многогранник

Кратко охарактеризуем геометрические свойства некоторых многогранников:

а) модель		б) эпюр
Рисунок 67. Пирамида

2. Призма — многогранник, две грани которого (основания призмы) представляют собой равные многоугольники с взаимно параллельными сторонами, а все другие грани параллелограммы. Призма называется прямой, если её ребра перпендикулярны плоскости основания. Если основанием призмы является прямоугольник, призму называют параллелепипедом (рис. 68).

а) модель		б) эпюр
Рисунок 68. Призма

3. Призматоид — многогранник, ограниченный двумя многоугольниками, расположенными в параллельных плоскостях (они являются его основаниями); его боковые грани представляют собой треугольники или трапеции, вершины которых являются и вершинами многоугольников оснований (рис.69).

а) модель		б) эпюр
Рисунок 69. Призматоид

4. Тела Платона. Многогранник, все грани которого представляют собой правильные и равные многоугольники, называют правильными . Углы при вершинах такого многогранника равны между собой.

Существует пять типов правильных многогранников. Эти многогранники и их свойства были описаны более двух тысяч лет назад древнегреческим философом Платоном, чем и объясняется их общее название.

Каждому правильному многограннику соответствует другой правильный многогранник с числом граней, равным числу вершин данного многогранника. Число ребер у обоих многогранников одинаково.

а) модель		б) эпюр
Рисунок 70. Тетраэдр

Гексаэдр — правильный шестигранник (рис. 71). Это куб состоящий из шести равных квадратов.

а) модель		б) эпюр
Рисунок 71. Гексаэдр

Октаэдр — правильный восьмигранник ( рис.72). Он состоит из восьми равносторонних и равных между собой треугольников, соединенных по четыре у каждой вершины.

а) модель		б) эпюр
Рисунок 72. Октаэдр

Додекаэдр — правильный двенадцатигранник, состоит из двенадцати правильных и равных пятиугольников, соединенных по три около каждой вершины (рис. 73).

а) модель		б) эпюр
Рисунок 73. Додекаэдр

Икосаэдр — состоит из 20 равносторонних и равных треугольников, соединенных по пять около каждой вершины (рис.74).

а) модель		б) эпюр
Рисунок 74. Икосаэдр

5. Звездчатые формы и соединения тел Платона. Кроме правильных выпуклых многогранников существуют и правильные выпукло-вогнутые многогранники. Их называют звездчатыми (самопересекающимися). Рассматривая пересечения продолжения граней Платоновых тел, мы будем получать звездчатые многогранники.

Источник