Что такое независимая выборка
Зависимые и независимые выборки в психологии. Примеры и порядок практического применения
Психологическое исследование предполагает изучение деятельности конкретного объекта (индивида или целой группы). Если эксперт анализирует единичный случай, то здесь достаточно сравнить все действия испытуемого с разработанной шкалой оценки, стандартами. Если же в поле зрения исследователя попала целая группа, то здесь уместно понятие выборка.
Психологическое исследование предполагает изучение деятельности конкретного объекта (индивида или целой группы). Если эксперт анализирует единичный случай, то здесь достаточно сравнить все действия испытуемого с разработанной шкалой оценки, стандартами. Если же в поле зрения исследователя попала целая группа, то здесь уместно понятие выборка.
Выборка в психологии
Выборка представляет собой группу объектов исследования, которые удовлетворяют конкретным требованиям. Отбор претендентов осуществляется из так называемой генеральной совокупности, то есть общей группы испытуемых, в которой присутствуют разные люди.

Требования к выборке разрабатываются автором научного изыскания, исходя из трех элементов: тема исследования, цель и задачи, объект и предмет. Фактически выборка конкретизирует объект исследования, кто именно будет подлежать изучению и анализу: возраст, пол, образование, опыт работы, наличие определенных привычек и качеств и пр.
Выборка предполагает, что к каждому исследованию будет подобрано определенное количество человек, удовлетворяющих требованиям автора научной работы. Использовать одну и ту же выборку в разных проектах не удастся.
Например, генеральной совокупностью психологического исследования могут быть все лица мужского пола. Выборкой в данном случае могут стать молодые люди в возрасте 25-30 лет.
Грамотно созданные выводы по выборке в дальнейшем могут быть перенесены на генеральную совокупность. В этом проявляется ее свойство репрезентативности.
Как производится отбор претендентов в выборку в психологическом исследовании?
Отбор испытуемых возможен на произвольной или плановой основе.
Первый вариант предполагает, что испытуемые были выбраны исследователем «методом тыка». Например, автору научной работы предстоит оценить уровень интеллектуального развития школьников. В данном случае их возраст не конкретизирован, поэтому он может остановиться на нескольких классах (притом разных!) и выбрать их них по 5-10 человек.

Плановая выборка представляет собой подбор претендентов путем сравнения их реального положения с заявленными исследователем параметрами. Например, при оценке уровня интеллектуального развития ученый может выбрать все группы: мальчики и девочки в возрасте 13-14 лет. То есть здесь выборка будет представлена в виде девушек и юношей подросткового периода.
Опытные исследователи отмечают, что целесообразно тщательно подбирать испытуемых, чтобы выборка обладала принципом репрезентативности.
При формировании выборки в психологическом исследовании предъявляют следующие требования:
Выборка должна помочь автору исследования собрать максимум материалов, который бы отразил полную картину генеральной совокупности, выборки.
Нужна помощь преподавателя?
Мы всегда рады Вам помочь!
Понятие зависимых и независимых выборок в психологии
В психологическом исследовании в большинстве случаев изучают либо один конкретный объект, либо несколько групп испытуемых. В зависимости от того, как будут сравнивать между собой результаты каждой из групп, выделяют зависимые и независимые выборки.
Если между испытуемыми разных групп была установлена некая зависимость, исследователь сравнивает результаты их работы между собой, то такая выборка считается зависимой. Притом на всех стадиях эксперимента или исследования должна быть очевидна связь конкретных испытуемых. Примером зависимой выборки могут быть мужья и жены. Например, психолог намерен выяснить отношение пары к семейным праздникам и традициям. Здесь он будет анализировать мнение жены и мнение мужа.
Если же взаимосвязь между выборками отсутствует, исследователь изучает результаты выборки в целом или отдельно взятого объекта исследования, то такая выборка считается независимой.
Примером независимой выборки является сравнение точек зрения мужчин и женщин в целом (по определенному поводу), анализ поведения психологов и математиков и пр. Фактически здесь сравнивают две противоположности или тех, кто не имеет явных сходств.
Важно отметить, что сравнение независимых выборок производится при помощи специальных методик: Стьюдента, Манна-Уитни, критерий знаков и пр.
Результаты психологического исследования в дальнейшем позволяют определить дальнейшие действия экспертов, нацеленные на решение конкретной проблемы. Они призваны оценить текущее положение дел, наличие стандартных решений и их эффективность, устранение существующих пробелов.
Решающим звеном научной работы является определение объекта исследования и выборки. От качества выборки, грамотности исследователя зависит дальнейшая судьба отрасли и жизнь общества.
Трудности с учебой?
Помощь в написании студенческих и
аспирантских работ!
Независимые выборки
Вы будете перенаправлены на Автор24
Понятие независимой выборки
Многие статистические анализы основаны на предположении, что выборки являются независимыми. Другие предназначены для оценки параметров, которые не являются независимыми.
Например, предположим, что инспекторы хотят сравнить две лаборатории по качеству, чтобы определить, дают ли их анализы крови схожие результаты. Они отправляют образцы крови, взятые у 10 детей, в обе лаборатории для анализа.
Поскольку обе лаборатории тестировали образцы крови одних и тех же 10 детей, результаты теста не являются независимыми. Чтобы сравнить средние результаты анализа крови в двух лабораториях, инспекторам потребуется выполнить парный t-тест, основанный на предположении, что образцы являются зависимыми.
Чтобы получить независимые образцы, инспекторам необходимо было бы случайным образом отобрать и проверить 10 детей в лаборатории А, а затем случайным образом выбрать и проверить другую группу из 10 разных детей в лаборатории В. Затем они могли бы сравнить средние результаты анализа крови из двух лабораторий, используя t-критерий с двумя выборками, основанный на предположении, что выборки независимы.
Статистические тесты основаны на предположении, что каждый субъект (или каждая экспериментальная единица) были отобраны независимо от остальных. Данные независимы тогда, когда любой случайный фактор, обладающий слишком высоким или слишком низким значением, влияет только на это значение. Если случайный фактор (тот, который не учитывался при анализе данных) может повлиять на несколько значений (но не на все), то данные не являются независимыми.
Понятие независимости довольно трудно определить. Рассмотрим следующие три ситуации:
Готовые работы на аналогичную тему
T-критерий для независимых выборок
T-критерий для двух независимых выборок может быть использован для определения наличия статистически значимой разницы между средними значениями двух независимых выборок. Иными словами, t-критерий подходит для проверки гипотезы о разнице между двумя независимыми выборками. Таким образом, тестируемая переменная должна иметь интервальное масштабирование (связь с уровнем масштабирования) и нормальное распределение. В отличие от Т-теста для парных переменных, в этом случае они не обязательно должны быть одинакового размера.
Т-критерий для двух независимых выборок используется для ответа на вопрос о том, различаются ли две группы по определенному признаку (потребительское поведение, стрессоустойчивость, отношение к различным проблемам и др.), или в случае, когда экспериментальная группа дает результаты, отличающиеся от результатов контрольной группы (успех в лечении, результаты некоторых тестов и т. д.). Поэтому этот t-тест подходит для таких вопросов, как «отличается ли потребительское поведение мужчин и женщин?» или «экспериментальная группа и контрольная группа по-разному реагируют на метод лечения?».
Процедура проведения t-теста для двух независимых выборок осуществляется на основе вопроса, взятого из маркетингового исследования.
Группу респондентов, состоящую примерно из половины мужчин и половины женщин, просят оценить качество продукта по шкале от 0 до 10, где 0 – это «очень плохо», а 10 – это «очень хорошо». Исследовательский вопрос можно сформулировать следующим образом: «По-разному ли оценивают качество продукта женщины и мужчины?». Цель исследования состоит в том, чтобы выяснить, как качество продукта влияет на его выбор у мужчин и женщин.
Чтобы проверить вопрос исследования статистически, необходимо сформулировать гипотезы. Другими словами, должно быть возможно выяснить, может ли разница в средних выборок быть обобщена на все популяцию, лежащую в основе выборок.
T-тесты являются параметрическими тестами, что подразумевает под собой возможность указания распределения вероятностей для совокупности переменных, из которой были взята выборка. Параметрические (и непараметрические) тесты имеют ряд допущений. Если эти предположения нарушаются, исследователь не может быть уверен в том, что тестовая статистика соответствует распределению t, и в этом случае p-значения могут быть неточными.
Представление результатов теста:
Выборка
Выборка — множество случаев (испытуемых, объектов, событий, образцов), с помощью определённой процедуры выбранных из генеральной совокупности для участия в исследовании.
Содержание
Объём выборки
Объём выборки — число случаев, включённых в выборочную совокупность. Из статистических соображений рекомендуется, чтобы число случаев составляло не менее 30—35.
Зависимые и независимые выборки
При сравнении двух (и более) выборок важным параметром является их зависимость. Если можно установить гомоморфную пару (то есть, когда одному случаю из выборки X сооветствует один и только один случай из выборки Y и наоборот) для каждого случая в двух выборках (и это основание взаимосвязи является важным для измеряемого на выборках признака), такие выборки называются зависимыми. Примеры зависимых выборок:
В случае, если такая взаимосвязь между выборками отсутствует, то эти выборки считаются независимыми, например:
Соответственно, зависимые выборки всегда имеют одинаковый объём, а объём независимых может отличаться.
Сравнение выборок производится с помощью различных статистических критериев :
Репрезентативность
Выборка может рассматриваться в качестве репрезентативной или нерепрезентативной.
Пример нерепрезентативной выборки
На действительных же выборах, как известно, победил Рузвельт, набрав более 60 % голосов. Ошибка «Литрери Дайджест» заключалась в следующем: желая увеличить репрезентативность выборки, — так как им было известно, что большинство их подписчиков считают себя республиканцами, — они расширили выборку за счёт людей, выбранных из телефонных книг и регистрационных списков. Однако они не учли современных им реалий и в действительности набрали ещё больше республиканцев: во время Великой депрессии обладать телефонами и автомобилями могли себе позволить в основном представители среднего и верхнего класса (то есть большинство республиканцев, а не демократов).
Виды плана построения групп из выборок
Выделяют несколько основных видов плана построения групп [2] :
Стратегии построения групп
Рандомизация
Попарный отбор
Стратометрический отбор
Приближённое моделирование
Источники
Рекомендуемая литература
Наследов А. Д. Математические методы психологического исследования. СПб.: Речь, 2004.
См. также
В некоторых типах исследований выборка разделяется на:
is:Úrtak lt:Imtis nl:Steekproef pl:Próba losowa sv:Stickprov
Зависимые и независимые выборки
Зависимые и независимые выборки. Обычна ситуация исследования, когда интересующее исследователя свойство изучается на двух или более выборках с целью их дальнейшего сравнения. Эти выборки могут находиться в различных соотношениях — в зависимости от процедуры их организации. Независимые выборка характеризуются тем, что вероятность отбора любого испытуемого одной выборки не зависит от отбора любого из испытуемых другой выборки. Напротив, зависимые выборки характеризуются тем, что каждому испытуемому одной выборки поставлен в соответствие по определенному критерию испытуемый из другой выборки.
Наиболее типичный пример зависимых выборок — повторное измерение свойства (свойств) на одной и той же выборке после воздействия (ситуация до-после). В этом случае выборки (одна — до, другая — после воздействия) зависимы в максимально возможной степени, так как они включают одних и тех же испытуемых. Могут быть и более слабые варианты зависимости. Например, мужья — одна выборка, их жены — другая выборка (при исследовании, например, их предпочтений). Или дети 5-7 лет — одна выборка, а их братья или сестры-близнецы — другая выборка.
В общем случае зависимые выборки предполагают попарный подбор испытуемых в сравниваемые выборки, а независимые выборки — независимый отбор испытуемых.
Следует отметить, что случаи частично зависимых (или частично независимых) выборок недопустимы: это непредсказуемым образом нарушает их репрезентативность.
Раздел 3. Формы учета результатов исследования
Обычно в ходе исследования интересующий исследователя признак измеряется не у одного-двух, а у множества объектов (испытуемых). Кроме того, каждый объект характеризуется не одним, а целым рядом признаков, измеренных в разных шкалах. Одни признаки представлены в номинативной шкале и указывают на принадлежность испытуемых к той или иной группе (пол, профессия, контрольная или экспериментальная группа и т. д.). Другие признаки могут быть представлены в порядковой или метрической шкале.
Для наглядного представления экспериментальных данных используются различные приемы, облегчающие прежде всего визуальный анализ полученной в эксперименте информации.
К таким приемам относят таблицы, ряды распределений, графики, гистограммы. Их применяют с той целью, чтобы полученные экспериментальные данные представить наглядным образом и можно было бы в явной форме увидеть характерные особенности и результаты эксперимента.
Первичный экспериментальный материал, полученный психологом, нуждается в соответствующей обработке. Обработка начинается с упорядочения и систематизации собранных данных.
Процесс систематизации результатов эксперимента, объединение их в относительно однородные группы по некоторому признаку называется группировкой.
Группировка — это не просто технический прием, позволяющий представить первичные данные в ином виде, но, прежде всего, такая операция, которая позволяет глубже выявить связи между изучаемыми явлениями. От того, как группируется исходный материал, во многих случаях зависят выводы о природе изучаемого явления. Поэтому группировка должна быть обдуманной, отвечать требованию поставленной задачи и соответствовать содержанию изучаемого явления.
Таблицы
Результаты измерения для дальнейшего анализа чаще всего представляют в виде таблицы исходных данных. Каждая строка такой таблицы обычно соответствует одному объекту, а каждый столбец — одному измеренному признаку. Таким образом, исходной формой представления данных является таблица типа «объект — признак». В ходе дальнейшего анализа каждый признак выступает в качестве переменной величины, или просто — переменной, значения которой меняются от объекта к объекту.
Таблицы бывают простыми и сложными.К простым относятся таблицы, применяемые при альтернативной группировке, когда одна группа испытуемых противопоставляется другой; например, здоровые — больным, высокие люди — низким и т.п. Пример простой таблицы приведен ниже. В ней представлены результаты обследования мануальной асимметрии у 110 учащихся 3—6-х классов.
Усложнение таблиц происходит за счет возрастания объема и степени дифференцированности представленной в них информации. К сложным таблицам относят так называемые многопольные таблицы, которые могут использоваться при выяснении причинно-следственных отношений между варьирующими признаками. Такие таблицы, как правило, имеют сложное строение, позволяющее одновременно осуществлять разные варианты группировки данных. Примером сложной таблицы служит Таблица 3.3, в которой представлены классические данные Ф. Гальтона, иллюстрирующие наличие положительной зависимости между ростом родителей и их детей. Таблица организована таким образом, что позволяет оценить частоту встречаемости в популяции однозначно фиксируемых соотношений роста родителей и роста ребенка. Например, при низком росте родителей в 66 дюймов (1 дюйм равен 2,54 см) только один из 144 обследованных детей имел рост в 60,7 дюймов, а 56 детей имели рост 66,7 дюйма. В то же время высокий рост детей (74,7 дюйма) был зафиксирован только в тех семьях, где родители имели рост не ниже 70 дюймов.
Эта таблица позволяет выявить тенденцию, заключающуюся в том, что у высоких родителей, как правило, дети имеют высокий рост, а у низкорослых родителей чаще бывают дети невысокого роста. Данный пример показывает, что таблицы имеют не только иллюстративное, но и аналитическое значение, позволяя обнаруживать разные аспекты связей между варьирующими признаками. Следует запомнить, что правильно составленные таблицы — это большое подспорье в экспериментальной работе, позволяющее одновременно осуществлять разные варианты группировки полученных данных.
Статистические ряды
Особую форму группировки данных представляют так называемые статистические ряды, или числовые значения признака, расположенного в определенном порядке. В зависимости от того, какие признаки изучаются, статистические ряды делят на атрибутивные, вариационные, ряды динамики, регрессии, ряды ранжированных значений признаков и ряды накопленных частот. Наиболее часто в психологии используются вариационные ряды, ряды регрессии и ряды ранжированных значений признаков.
Вариационным рядом распределения называют двойной ряд чисел, показывающий, каким образом числовые значения признака связаны с их повторяемостью в данной выборке. Например, психолог провел тестирование интеллекта по тесту Векслера у 25 школьников, и сырые баллы по второму субтесту оказались следующими: 6, 9, 5, 7, 10, 8, 9, 10, 8, 11, 9, 12, 9, 8, 10, 11, 9, 10, 8, 10, 7, 9, 10, 9, 11. Как видим, некоторые цифры попадаются в данном ряду по несколько раз. Следовательно, учитывая число повторений, данные ряд можно представить в более удобной, компактной форме:
Это и есть вариационный ряд. Числа, показывающие, сколько раз отдельные варианты встречаются в данной совокупности, называются частотами, или весами, вариант. Они обозначаются строчной буквой латинского алфавита.fi и имеют индекс “i”, соответствующий номеру переменной в вариационном ряду.
Процентное представление частот полезно в тех случаях, когда приходится сравнивать вариационные ряды, сильно различающиеся по объемам. Например, при тестировании школьной готовности детей города, поселка городского типа и села были обследованы выборки детей численностью 1000, 300 и 100 человека соответственно. Различие в объемах выборок очевидно. Поэтому сравнение результатов тестирования лучше проводить, используя проценты частот.
Приведенный выше ряд (3.1) можно представить по другому. Если элементы ряда расположить в возрастающем порядке, то получится так называемый ранжированный вариационный ряд:
Подобная форма представления (3.3) более предпочтительна, чем (3.1), поскольку лучше иллюстрирует закономерность варьирования признака.
Частоты, характеризующие ранжированный вариационный ряд, можно складывать, или накапливать. Накопленные частоты получаются последовательным суммированием значений частот от первой частоты до последней.
В качестве примера вновь обратимся к ряду 3.3. Преобразуем его в ряд 3.4 в котором введем дополнительную строчку и назовем ее «кумуляты частот»:
Рассмотрим подробно как получилась последняя строчка. В начале ряда частот стоит 1. В кумулятивном ряду на втором месте стоит 2 — это сумма первой и второй частоты, т.е. 1 + 1, на третьем месте стоит 4 это сумма второй (уже накопленной частоты) и третьей частоты, т.е. 2 + 2, на четвертом 8 = 4 + 4 и т.д.
Размах (иногда эту величину называют разбросом) выборки обозначается буквой R. Это самый простой показатель, который можно получить для выборки — разность между максимальной и минимальной величинами данного конкретного вариационного ряда, т.е.
Понятно, что чем сильнее варьирует измеряемый признак, тем больше величина R, и наоборот.
Однако может случиться так, что у двух выборочных рядов и средние, и размах совпадают, однако характер варьирования этих рядов будет различный. Например, даны две выборки:
При равенстве средних и разбросов для этих двух выборочных рядов характер их варьирования различен. Для того чтобы более четко представлять характер варьирования выборок, следует обратиться к их распределениям.
Таблицы и графики распределения частот
Как правило, анализ данных начинается с изучения того, как часто встречаются те или иные значения интересующего исследователя признака (переменной) в имеющемся множестве наблюдений. Для этого строятся таблицы и графики распределения частот. Нередко они являются основой для получения ценных содержательных выводов исследования.
Если признак принимает всего лишь несколько возможных значений (до 10-15), то таблица распределения частот показывает частоту встречаемости каждого значения признака. Если указывается, сколько раз встречается каждое значение признака, то это — таблица абсолютных частот распределения, если указывается доля наблюдений, приходящихся на то или иное значение признака, то говорят об относительных частотах распределения.
Во многих случаях признак может принимать множество различных значений, например, если мы измеряем время решения тестовой задачи. В этом случае о распределении признака позволяет судить таблица сгруппированных частот, в которых частоты группируются по разрядам или интервалам значений признака.
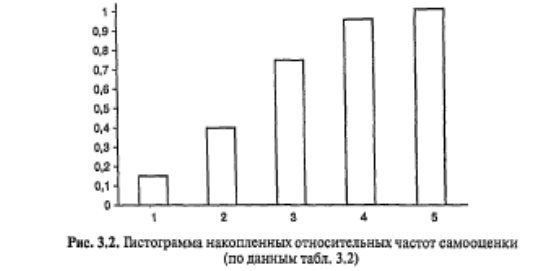
Еще одной разновидностью таблиц распределения являются таблицы распределения накопленных частот. Они показывают, как накапливаются частоты по мере возрастания значений признака. Напротив каждого значения (интервала) указывается сумма частот встречаемости всех тех наблюдений, величина признака у которых не превышает данного значения (меньше верхней границы данного интервала). Накопленные частоты содержатся в правых столбцах табл. 3.2 и 3.3.
Для более наглядного представления строится график распределения частот или график накопленных частот — гистограмма или сглаженная кривая распределения.
Гистограмма накошенных частот отличается от гистограммы распределения тем, что высота каждого столбика пропорциональна частоте, накопленной к данному значению (интервалу). На рис. 3.2 изображена гистограмма накопленных частот для данных табл. 3.2.
Построение полигона распределения частот напоминает построение гистограммы. В гистограмме вершина каждого столбца, соответствующая частоте встречаемости данного значения (интервала) признака, — отрезок прямой. А для полигона отмечается точка, соответствующая середине этого отрезка. Далее все точки соединяются ломаной линией (рис. 3.3). Вместо гистограммы или полигона часто изображают сглаженную кривую распределения частот. На рис. 3.4 изображена гистограмма распределения для примера из табл. 3.3 (столбики) и сглаженная кривая того же распределения частот.
Таблицы и графики распределения частот дают важную предварительную информацию о форме распределения признака: о том, какие значения встречаются реже, а какие чаще, насколько выражена изменчивость признака. Обычно выделяют следующие типичные формы распределения. Равномерное распределение – когда все значения встречаются одинаково (или почти одинаково) часто. Симметричное распределение — когда одинаково часто встречаются крайние значения. Нормальное распределение — симметричное распределение, у которого крайние значения встречаются редко и частота постепенно повышается от крайних к серединным значениям признака. Асимметричные распределения — левосторонние (с преобладанием частот малых значений), правосторонние (с преобладанием частот больших значений).
Уже сами по себе таблицы и графики распределения признака позволяют делать некоторые содержательные выводы при сравнении групп испытуемых между собой. Сравнивая распределения, мы можем не только судить о том, какие значения встречаются чаще в той или иной группе, но и сравнивать группы по степени выраженности индивидуальных различий — изменчивости по данному признаку.
Таблицы и графики накопленных частот позволяют быстро получить дополнительную информацию о том, сколько испытуемых (или какая их доля) имеют выраженность признака не выше определенного значения.
Раздел 4. Описательные статистики
(Статистическое распределение и его числовые характеристики)
Переменная может принимать много значений. На начальном этапе обработки данных вместо того, чтобы рассматривать все значения переменной, рекомендуется проанализировать т. к. описательные статистики. Они дают общее представление о значениях или разбросе значений, которые принимает переменная.
К первичным описательным статистикам (Descriptive Statistics) обычно относят числовые характеристики распределения измеренного на выборке признака. Каждая такая характеристика отражает в одном числовом значении свойство распределения множества результатов измерения: с точки зрения их расположения на числовой оси либо с точки зрения их изменчивости. Основное назначение каждой из первичных описательных статистик — замена множества значений признака, измеренного на выборке, одним числом (например, средним значением как мерой центральной тенденции). Компактное описание группы при помощи первичных статистик позволяет интерпретировать результаты измерений, в частности, путем сравнения первичных статистик разных групп.