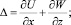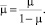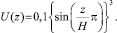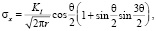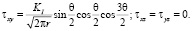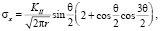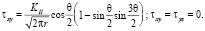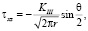Что такое напряженно деформированное состояние

Напряженно-деформированное состояние

Полезное

Смотреть что такое «Напряженно-деформированное состояние» в других словарях:

Напряженно-деформированное состояние — (НДС) состояние изделия, возникающее в результате воздействия нагрузок. Источник: МДС 53 2.2004. Диагностирование стальных конструкций (согласован Росстроем 20.01.2005) … Официальная терминология

Напряженно-деформированное состояние — – пространственное распределение напряжений и деформаций в конструкции моста. [Справочник дорожных терминов, М. 2005 г.] Рубрика термина: Теория и расчет конструкций Рубрики энциклопедии: Абразивное оборудование, Абразивы, А … Энциклопедия терминов, определений и пояснений строительных материалов

Напряженно-деформированное состояние — 12. Напряженно деформированное состояние состояние преднапряженных железобетонных строительных конструкций, ограждающих ЗЛА, характеризующееся усилиями натяжения арматурных пучков, проходящих внутри бетона. Источник: НП 010 98: Правила устройства … Словарь-справочник терминов нормативно-технической документации

напряженно-деформированное состояние — [strain stressed state] совместно описываемое динамическое и кинематическое состояние твердого тела, выраженное через напряжение и деформации и однозначно определяющее его пластическое поведение. Напряженно деформированное состояние обычно… … Энциклопедический словарь по металлургии

Напряженно-деформированное состояние — пространственное распределение напряжений и деформаций в конструкции моста. Источник: Справочник дорожных терминов … Строительный словарь

Напряженно-деформированное состояние (НДС) — состояние изделия, возникающее в результате воздействия нагрузок. Источник: МДС 53 2.2004: Диагностирование стальных конструкций Смотри также родственные термины: Напряженно деформированное состояние (НДС) газопровода состояние, при котором в… … Словарь-справочник терминов нормативно-технической документации

напряженно-деформированное состояние породного массива — Состояние породного массива, характеризуемое совокупностью в нем компонентов напряжений и деформаций. [ГОСТ Р 50544 93] Тематики горные породы EN stressed and strained state of rock massif DE Spannungs und Formanderungszustand des Gebirges FR… … Справочник технического переводчика

Напряженно-деформированное состояние (НДС) газопровода — состояние, при котором в металле труб газопровода возникают внутренние напряжения, вызванные воздействием внешних и внутренних нагрузок и воздействий. Источник: РД 12 411 01: Инструкция по диагностированию технического состояния подземных… … Словарь-справочник терминов нормативно-технической документации

напряженно-деформированное состояние породного массива — 43 напряженно деформированное состояние породного массива Состояние породного массива, характеризуемое совокупностью в нем компонентов напряжений и деформаций Источник: ГОСТ 30330 95: Породы горные. Термины и определения оригинал документа 43… … Словарь-справочник терминов нормативно-технической документации

напряженно-деформированное состояние (НДС) сооружения или основания — 3.28 напряженно деформированное состояние (НДС) сооружения или основания: Состояние объекта, характеризуемое контролируемыми уровнями значений напряжений и деформаций. Источник … Словарь-справочник терминов нормативно-технической документации

Источник

Что такое напряженно деформированное состояние

Идеи повышения эксплуатационной надежности оснований современных зданий и сооружений начали находить возможности своего приложения в практику проектирования достаточно давно. Одно из направлений – увеличение несущей способности грунтового основания за счет армирования грунта. Сама идея об использовании различных разновидностей вертикального и горизонтального армирования слабого грунтового основания в принципе была известна. Так, имели определенное распространение методы глубинной стабилизации слабых грунтов цементными и цементнопесчаными растворами [1, 5, 6]. Увеличение несущей способности горизонтальным армированием основания предложено французcкими учеными J. Binguet, K. Lee [7]. Авторами [7] показано, что горизонтальное армирование основания при трех слоях армирования синтетическими материалами в 1,6 раза увеличило несущую способность основания. Исследования горизонтально армированных оснований проводились также в университете штата Сан-Диего. Авторами было доказано, что несущая способность горизонтально армированного песчаного основания в зависимости от его плотности увеличивается от 1,2 до 1,6 раз. Перечисленные выше сведения об армировании грунтового основания можно отнести к «пассивным» системам повышения несущей способности оснований. В работах [2, 3] ставится вопрос об «активных» методах управления эксплуатационной надежностью и напряженно-деформированным состоянием основания. Идея активности методов управления эксплуатационной надежностью строительных конструкций вообще и оснований зданий и сооружений в частности неразрывно связана с теорией автоматического управления, методология которого применительно к регулированию напряженно-деформированного состояния (НДС) строительных конструкций существует только в виде отдельных положений.

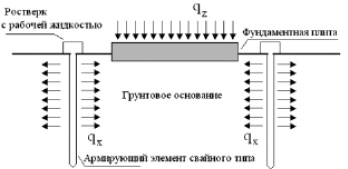
В работах Землянского А.А. принцип активности методов управления предлагается осуществлять за счет активного горизонтального армирования грунта с помощью шпунтовой стенки или полых рабочих свай с обеспечением возможности перемещений их боковых поверхностей (рис. 1). Активное армирование основания за счет давления преднапряжения в армирующей системе позволяет, как это экспериментально подтверждено в [2–4], повысить прочность и устойчивость слабых грунтов.

Рис. 1. Схема активного армирования основания

Непосредственной причиной повышения несущей способности грунтового основания, армированного активной горизонтальной системой, является предварительное напряжение грунтовой массы основания под фундаментной плитой. Теоретически учет такого преднапряжения связан с проявлением распределительных свойств грунта. Для этого необходима математическая модель основания, учитывающая полный вектор перемещений (вертикальные и горизонтальные перемещения).

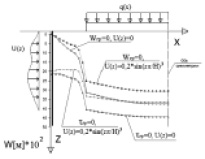
Для выявления особенностей НДС преднапряженного основания использована модель, представленная на рис. 2, а. Данная модель представляет собой грунтовый массив, ограниченный с двух сторон достаточно протяженными по длине армирующими элементами, создающими кинематическое нагружение. Эти условия позволяют перейти от решения трехмерной задачи к решению плоской симметричной задачи и сократить тем самым количество вычислений.

Рис. 2. Расчетная схема преднапряженного основания: а – при отсутствии вертикальной нагрузки; б – при наличии нагруженной фундаментной плиты

Рассматривая грунтовый массив как линейно деформируемую среду, в качестве неизвестных приняты вертикальные и горизонтальные компоненты (W(x, z), U(x, z)) вектора перемещений. В этом случае разрешающими уравнениями являются уравнения Ляме для плоской задачи:

(1)

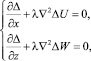
где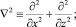

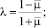
Расчетная схема преднапряженного основания без вертикального давления с граничными значениями перемещений и напряжений представлена на рис. 2. Для дискретизации этой модели в области интегрирования использован метод конечных разностей. В качестве исходных данных приняты следующие параметры: H = 10 м, L = 40 м, Е_гр = 20000 кПа, ν = 0,5, где H и L – размеры области интегрирования; Е_гр – модуль деформации грунта; ν – коэффициент Пуассона.

Предварительное напряжение грунта в данном случае задается в виде функции кинематического перемещения стенок армирующего элемента

Эпюры перемещений основания W(x, z), U(x, z) представлены на рис. 3.

Рис. 3. Эпюры перемещений слоя основания: а – вертикальных (W); б – горизонтальных (U)

На рис. 3, а можно наблюдать вертикальный выпор грунта вблизи зоны кинематического нагружения, убывающий по глубине слоя основания. Этот эффект обуславливает снижение осадок фундаментной конструкции при вертикальной нагрузке на армированный массив. В связи с принятой формой эпюры нагружения U(z) значения вертикальных перемещений вдоль оси Z приобретают обратный знак. Горизонтальные перемещения затухают ближе к оси симметрии (рис. 3, б).

НДС преднапряженного основания напрямую зависит от условий взаимодействия армирующего элемента с грунтовым массивом. Эпюры на рис. 3 соответствуют граничному условию, предполагающему отсутствие вертикальных перемещений грунта по поверхности армирующего элемента (W_гр = 0). При условии отсутствия касательных напряжений на границе армирования (τ_гр = 0), предполагающем свободное перемещение грунта по армирующему элементу, картина распределения перемещений грунтового массива качественно изменяется. Для наглядности сравним перемещения поверхности армированного основания с различными граничными условиями (рис. 4). Функция кинематического перемещения по высоте слоя при этом принята постоянной (U(z) = 0,2 м). Как видно из графиков на рис. 4, а, при условии (τ_гр = 0) максимальные вертикальные перемещения поверхности основания W(x) концентрируются у границы активного армирования. При условии (W_гр = 0) максимальный выпор грунта находится на некотором удалении от этой границы.

Условию (τ_гр = 0) соответствует большее абсолютное значение вертикальных перемещений. Также видно, что независимо от граничных условий вертикальные перемещения поверхности основания затухают по мере удаления от границы основания, взаимодействующей со шпунтом. То же происходит и с горизонтальными перемещениями U(x) (рис. 4, б).

При рассмотрении системы «фундаментная плита – преднапряженное основание», помимо граничных условий в постановке задачи, на НДС системы также существенное влияние оказывает положение армирующего элемента относительно фундаментной плиты и по высоте слоя основания. Попробуем проследить влияние рассмотренных различий в постановке задачи на НДС системы «фундаментная плита – преднапряженное основание». Для выявления особенностей НДС грунтового массива при сложном напряженном состоянии использована модель, представленная на рис. 2, б. В отличие от предыдущей модели, на рассматриваемый преднапряженный объем грунта опирается плита с соотношением сторон l/b > 10 нагруженная равномерно распределенной нагрузкой. Считается, что поверхность контакта балки и основания является абсолютно гладкой, а реакции контакта направлены по нормали к этой поверхности. Также предполагается, что вертикальные перемещения поверхности основания и нижней поверхности балки происходят совместно без отрыва, и величина вертикального давления, передаваемого на поверхность основания со стороны балки, равна вертикальному отпору R_z(x). Вертикальный отпор связан условием равновесия балки с величиной ее изгибной жесткости (EJ) и характером нагрузки q(x):

(2)

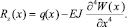
Рис. 4. Эпюры перемещений поверхности основания: а – вертикальных – W(x); б – горизонтальных – U(x)

Решение задачи находится на основе совместного решения системы уравнений Ляме (1) с уравнением изгиба балки (2), входящим в систему уравнений через граничные условия, записанные для участка поверхности основания, контактирующего с балкой.

На рис. 5 представлены эпюры вертикальных перемещений поверхности основания W(x) при различных граничных условиях контакта грунта с армирующим элементом.

Для исходных данных приняты следующие параметры: H = 30 м, L = 40 м, Егр = 20000 кПа, Е_b = 21000000 кПа, ν = 0,5, h_b = 1 м, q(x) = 500 кН/м, L/b = 1,5.

Рис. 5. Перемещения поверхности основания W(x) под фундаментной плитой

Как видно из графиков (рис. 5), кинематическое нагружение грунта способствует снижению вертикальных осадок фундаментной плиты на 18 %. Наибольший эффект наблюдается при отсутствии вертикальных перемещений грунта по поверхности армирующего элемента (W_гр = 0). Отсутствие касательных напряжений (τ_гр = 0) в данном случае ухудшает работу грунтового массива и увеличивает осадки на 20 %.

Оценивая снижение осадок фундаментной плиты, следует принимать во внимание упругую работу грунта под нагрузкой. В рассматриваемой линейной постановке задачи снижение осадок плиты прямо пропорционально увеличению величины кинематического нагружения. Особенности данной математической модели также можно отметить на эпюрах распределения напряжений в основании. Качественная картина распределения нормальных и касательных напряжений σ_z и τ_zx для системы «фундаментная плита – преднапряженное основание» представлена на рис. 6.

Рис. 6. Эпюры напряжений слоя основания: а – нормальных (σz); б – касательных (τzx)

Вдоль поверхности армирующего элемента присутствуют характерные очертания эпюр нормальных и касательных напряжений, обусловленные кинематическим нагружением (рис. 6). Максимальная же концентрация напряжений находится под торцом балки. Напряжения в этом месте возрастают по мере сгущения конечно-разностной сетки. При таких значениях напряжений в грунте, как правило, происходит развитие зон предельного равновесия, и грунт переходит в пластическую стадию работы. Для данной модели это обстоятельство накладывает соответствующие ограничения на величину вертикальной нагрузки.

При анализе величины абсолютных осадок фундаментной плиты следует учесть влияние положения армирующего элемента относительно фундаментной плиты и по глубине слоя основания. По мере смещения армирующего элемента к краю плиты наблюдается снижение ее осадок. Вместе с тем усиливается и влияние рассмотренных краевых эффектов.

Таким образом, напряженно-деформируемое состояние системы «фундаментная плита – преднапряженное основание» определяется многими факторами. Использование приведенной математической модели в рамках упругой задачи позволяет выделить наиболее существенные из них для более точной оценки НДС основания с активным армированием. В частности, при формулировке граничных условий необходимым является учет сил трения между грунтом и армирующим элементом, отражающий характер их взаимодействия. Также необходимым является учет неупругих свойств грунтовой среды. Для данной модели линейно-деформированного основания при активном армировании наблюдается снижение осадок фундаментной плиты под нагрузкой пропорционально увеличению величины кинематического нагружения, что дает повод для дальнейшего изучения вопросов математического моделирования, прочности и устойчивости преднапряженных оснований и их совместной работы с сооружениями.

Рецензенты:

Денисова А.П., д.т.н., профессор, Саратовский государственный технический университет имени Гагарина Ю.А., г. Саратов;

Гарибов Р.Б., д.т.н., генеральный директор, ЗАО «Научно-технический центр «Волгапромстройбезопасность», г. Энгельс.

Источник

Что такое напряженно деформированное состояние

Усталостное разрушение – одно из самых распространенных видов замедленного разрушения стали, при котором происходит зарождение и постепенный рост начальных трещин до достижения ими критических размеров. Выявлено, что такой вид разрушения является основной причиной эксплуатационных повреждений большинства современных металлоконструкций и их сварных соединений.

Несмотря на то, что ответственные элементы таких конструкций подлежат периодическому техническому освидетельствованию, их усталостное разрушение часто протекает без видимых признаков. В связи с этим актуальной является проблема прогнозирования усталостного разрушения стальных деталей.

Цель исследования: определить методики, позволяющие оценить напряженно-деформированное состояние материала в докритический период развития усталостных трещин. Ее достижение известными методами современной теории связано со значительными математическими трудностями, в частности с решениями сложных нелинейных уравнений в частных производных. Усталость, как один из механизмов разрушения, является причиной эксплуатационных повреждений подавляющего большинства современных инженерных сооружений. Поэтому проблема сохранения прочности элементов конструкций при действии переменных нагрузок является одной из наиболее актуальных [1].

Материалы и методы исследования

Период докритического роста усталостной трещины определяет остаточную долговечность элемента конструкции. Стадия развития усталостной трещины в зависимости от конструктивных особенностей изделия (режимов его нагрузки, условий эксплуатации и др.) может составлять значительную часть общей долговечности элемента металлоконструкции. Поэтому исследование кинетики распространения усталостных трещин с учетом всех факторов влияния является важной научно-технической задачей и имеет большое практическое значение.

Как показывают экспериментальные исследования [2, 3], подавляющему большинству современных инженерных конструкций и сооружений присуще наличие макроскопических дефектов (трещины, разного рода несплошности, непровары в сварных соединениях, включения и др.), возникающих еще в процессе изготовления этих конструкций или появляющихся в процессе их эксплуатации.

В результате действия циклической нагрузки эти дефекты могут развиваться путем распространения трещин до полного разрушения элемента металлоконструкции, причем этот процесс может происходить при значительно меньшем предельном уровне нагрузки и характеризуется длительным накоплением необратимых повреждений в материале, что приводит к зарождению, развитию трещин и полному разрушению тела. Такое разрушение при циклической, то есть переменной во времени, нагрузке называется усталостным разрушением. Как правило, усталостное разрушение происходит непредсказуемо, часто без признаков поврежденности на поверхности металла элемента конструкции.

В сложном процессе усталостного разрушения достаточно четко просматриваются отдельные его стадии, отличающиеся необратимыми изменениями в материале. Общепринято разделять этот процесс на три основные стадии:

— инкубационный период, который характеризуется неоднородной концентрацией микропластических оползней, главным образом в поверхностных слоях деформируемого тела вследствие их повышенной технологической дефектности и пониженного сопротивления текучести;

— период зарождения субмикротрещины, слияния и образования минитрещин – нарушение структуры материала на уровне его блоков, зерен, включений, а в поверхностном слое – образование ступенек экструзии и интрузии;

— период распространения трещины, который начинается в тот момент, когда одна из микротрещин становится доминантной и перерастает в макротрещину. Контролирующим фактором распространения трещины является величина циклической пластической деформации в области пластической зоны у вершины трещины.

Исследование процессов, происходящих при усталостном развитии трещин, в первую очередь базируется на анализе напряженно-деформированного состояния (НДС) в месте расположения трещины. В границах механики разрушения, которая базируется на принципах идеальной упругости рассматриваемого тела и понимает трещину как разрез с толщиной равной нулю с поверхностью, на которой отсутствует напряжение, такая задача решается как краевая задача теории упругости [3].

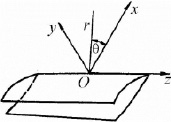
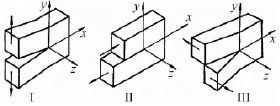
Общий случай распределения изменений в радиусе произвольной точки О (рис. 1) границ трещины можно показать в виде трех видов изменений (рис. 2), которые находятся в соответствии главным видам смещений на поверхности этой трещины: нормального отрыва (I), поперечного (II) и продольного (III) смещения [4, 5].

Рис. 1. Локальная система координат у вершины трещины

Первый представленный вид – это смещение верхних слоев трещины в разновекторных направлениях (симметрично к поверхностям ху и хz). Второй вид – это скольжение, в случае которого верхние слои трещины перемещаются один по другому в направлении, которое будет перпендикулярным по отношению к их фронту. Третий вид демонстрирует перемещение одного слоя трещины по-другому в направлении, параллельном фронту такой трещины.

Рис. 2. Схема основных макромеханизмов распространения трещины

Согласно исследованиям А.Е. Андрейкива [4, 5] при реализации каждого из упомянутых типов деформирования распределение напряжений в окрестности контура трещины запишется в виде (1), (2), (3).

Для нормального отрыва [4, 5]:

(1)

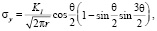
Для поперечного смещения [4, 5]:

(2)

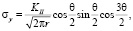
Для продольного смещения [4, 5]:

(3)

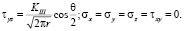
Дополнительно в соотношениях (1), (2) необходимо принять σz = 0 для плоского напряженного состояния и 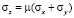для плоской деформации.

Таким образом, коэффициенты интенсивности напряжений являются основными расчетными характеристиками линейной механики разрушения, однозначно определяют НДС в зоне предразрушений.

При циклической нагрузке тела с трещиной анализ реальной механической ситуации в зоне предразрушения осложняется еще больше. Сложные процессы постепенного накопления повреждений во времени, сопровождающиеся непрерывным изменением реологических и прочностных свойств материала в этой зоне, практически не поддаются математическому описанию и могут быть смоделированы только в общих чертах.

Существование неупругих (пластичных) деформаций приводит к тому, что при разгрузке металлического материала, непосредственно у вершины трещины возникают остаточные напряжения сжатия, которые в свою очередь вызывают обратное пластическое течение материала. Таким образом, в некоторой части начальной зоны пластичности формируется область, где при циклических нагрузках происходит реверсивное течение, что приводит к накоплению пластических деформаций. Эта область и является, по сути, циклической пластической зоной.

Согласно некоторым качественным оценкам [4], ее размеры примерно в четыре раза меньше размеров пластической зоны при статической нагрузке. Наличие у вершины трещины зоны пластической деформации приводит к несоответствию настоящего НДС такому, что предполагается соотношениями, полученными при решении задачи для упругих тел.

Однако, если зона нелинейного поведения свойств материала достаточно мала, то существует область, которая по размерам является промежуточной между размерами пластической зоны и длиной трещины или размерами тела, в которой асимптотическое решение (1)–(3) еще описывает истинное распределение напряжений.

А поскольку в этом случае значения коэффициентов интенсивности напряжений полностью определяют поле напряжений вне зоны пластичности, то тем самым они контролируют напряженное состояние материала в середине этой области, а именно – интенсивность процессов разрушения, которые в ней происходят.

Таким образом, критерии линейной механики разрушения сохраняют свою прогнозирующую способность и в реальных ситуациях, если только выполняются условия малости пластических зон (условия квазихрупкого состояния). Необходимые ограничения, при которых указанные условия имеют место, устанавливаются специальными математическими соотношениями – условиями автомодельности [5].

Эти соотношения, в частности, являются основным критерием выбора оптимальных размеров образцов, при испытании которых разрушение происходит квазихрупким механизмом и тем самым обеспечивается адекватное определение характеристик трещиностойкости. Следует отметить, что развитие усталостных трещин происходит при сравнительно низких уровнях действующих напряжений и сопровождается меньшими, чем в статике, пластическими зонами.

Поэтому возможности применения коэффициентов интенсивности напряжений как расчетных параметров для описания усталостного разрушения значительно шире, чем при однократной (монотонной) нагрузке. Они могут быть эффективно использованы при расчете многих реальных инженерных объектов. В тех случаях, когда условия квазихрупкого разрушения не обеспечиваются, для расчета нужны более точные методы, учитывающие наличие развитых пластических зон у вершины трещины.

Для всех реальных материалов, при напряжениях превышающих σT, линейная связь между напряжениями и деформациями нарушается и дальнейшая нагрузка сопровождается пластическим течением. В результате этого перед концом трещины всегда существует пластическая зона определенных размеров. Для расчета этой зоны необходимо исследовать распределение напряжений и деформаций у вершины трещины в упруго-пластической постановке, что связано со значительными математическими трудностями.

Рассчитать в ней локальные напряжения возможно с помощью компьютерного математического моделирования напряженно-деформированного состояния методом конечных элементов (МКЭ).

Суть метода конечных элементов заключается в том, что тело представляется в виде некоторого каркаса, состоящего из элементов прямоугольной или треугольной формы. Совокупность элементов образует законченную решетку, внешняя форма которой соответствует форме тела.

Распределение напряжений в теле рассчитывают, рассматривая равновесие сил в общих точках или узлах решетки, а распределение деформаций – принимая во внимание перемещение обоих узлов.

Результаты исследования и их обсуждение

Авторами [6, 7] была разработана схема создания математической модели образца с надрезом, согласно которой исследуемый объект – идеализированная расчетная схема – система линейных алгебраических уравнений.

Непосредственный переход к расчетной схеме дает возможность естественно формулировать граничные условия, произвольно располагать узлы сетки элементов, сгущая ее в местах ожидаемого большого градиента напряжений и деформаций. Используемая модель позволяет рассчитывать напряжения, в том числе и в пластической зоне перед надрезом, с учетом эффекта упрочнения. Конечно-элементная сеть строится посредством стыковки любого числа фрагментов.

Графический образ сетки конечных элементов вблизи концентратора напряжений представлен на рис. 3.

Рис. 3. Графический образ сетки конечных элементов вблизи концентратора напряжений [6]

Входные характеристики программы: предел текучести, модуль Юнга, показатель и коэффициент упрочнения определяется из испытаний на растяжение гладких образцов МРГ-3. В результате расчетов с помощью МКЭ определяется напряженно-деформированное состояние во всех узлах сетки конечных элементов.

С помощью этой методики можно определить локальные напряжения в зоне зарождения трещины по известному пределу текучести стали [7].

Выводы

Для любой заданной нагрузки можно определить локальное напряжение до и после образования пластически деформированной зоны разрушения.

Использование приемов математического моделирования напряженно-деформированного состояния стали и стальных деталей в местах формирования микротрещин предоставляет возможность диагностировать критические напряжения в местах зарождения трещин. Метод конечных элементов можно применять для определения докритического периода развития усталостных трещин.

Источник