Что такое нормали в blender

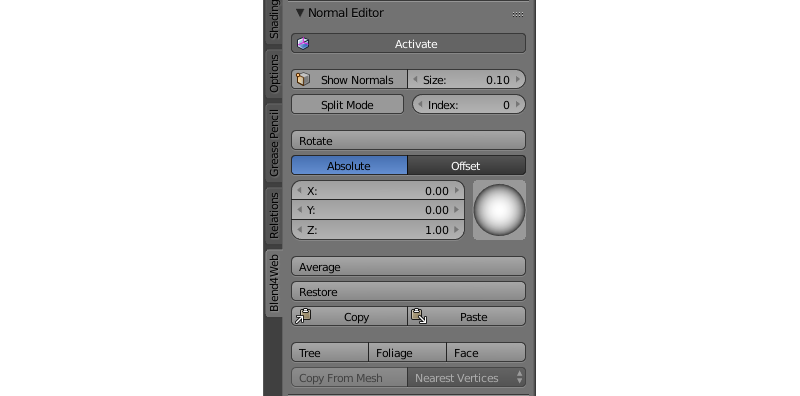
Редактор нормалей¶

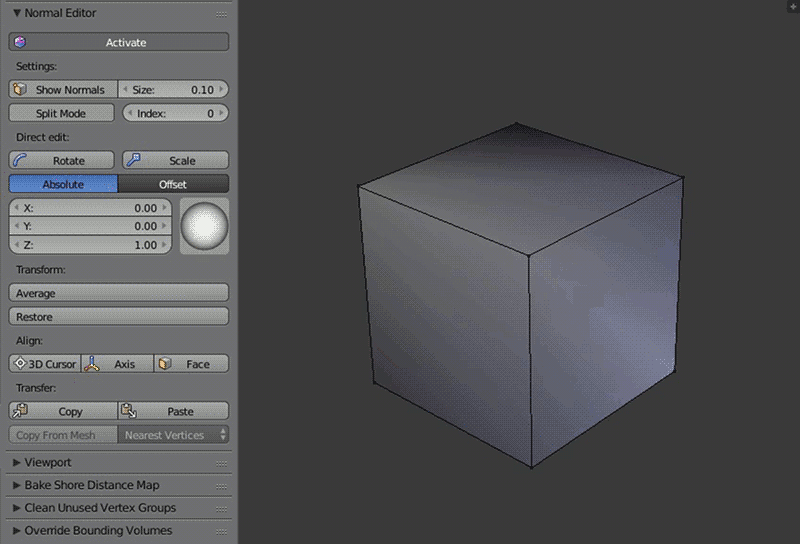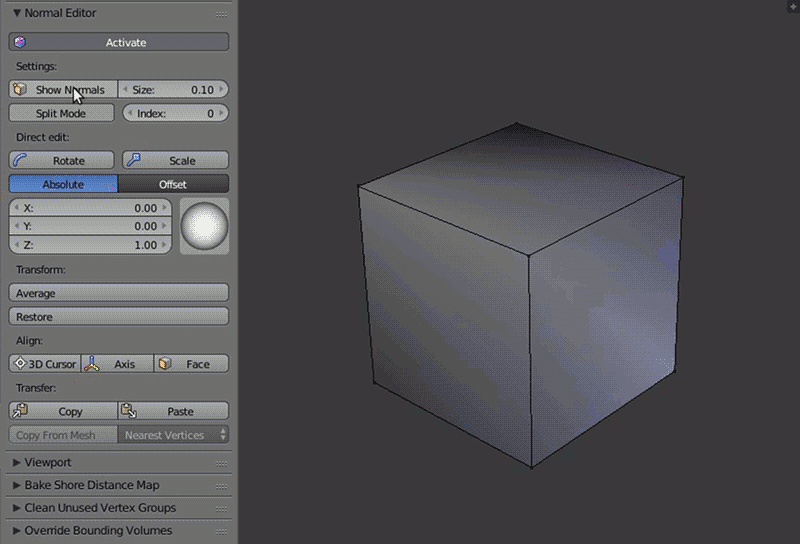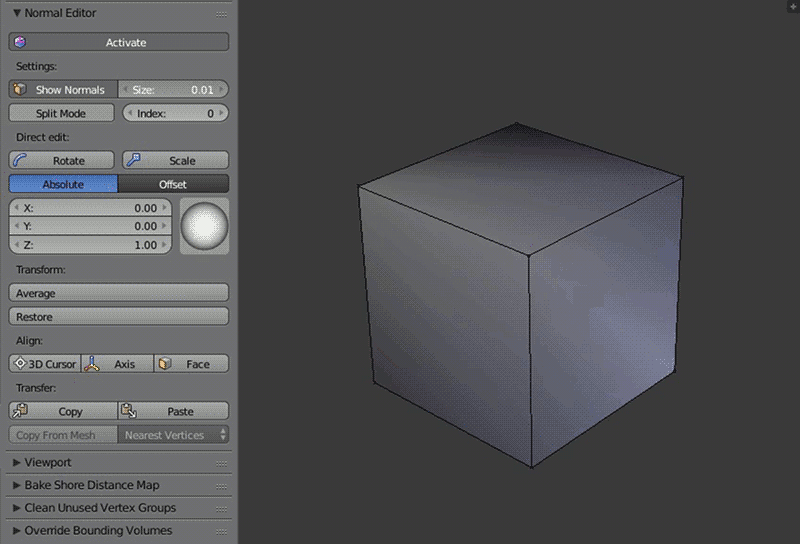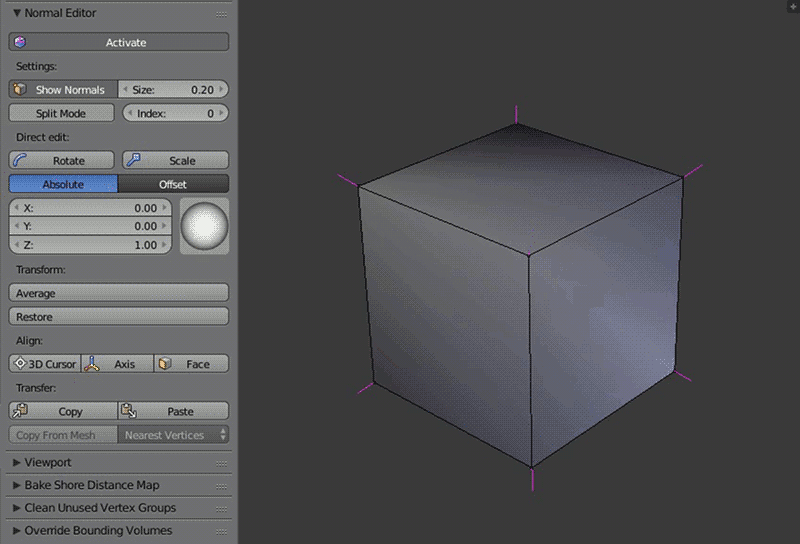
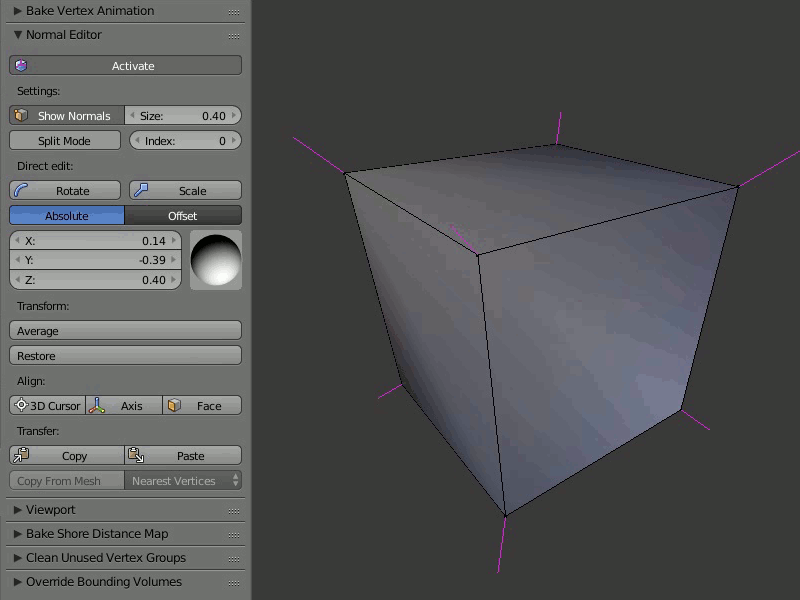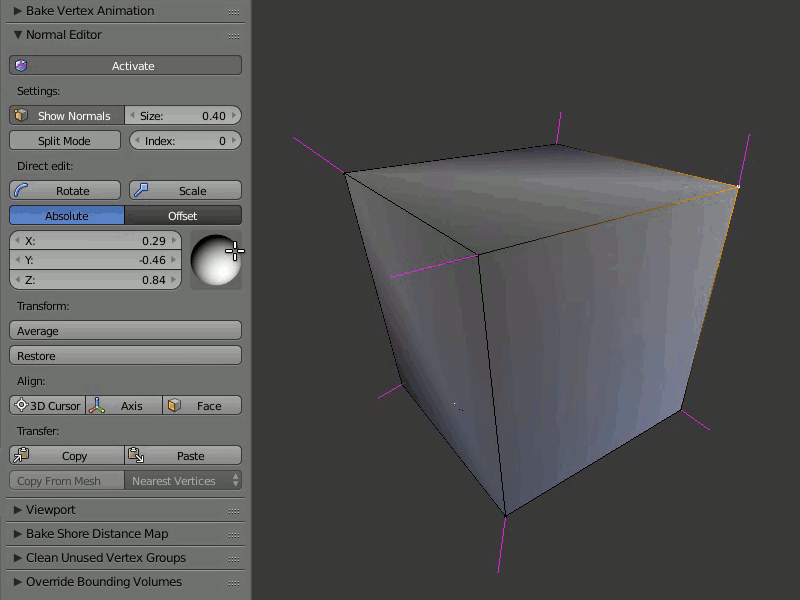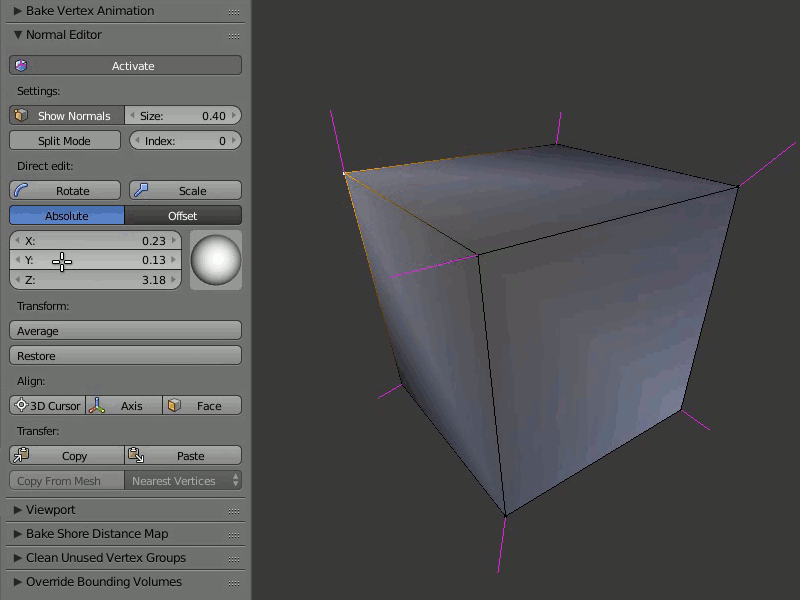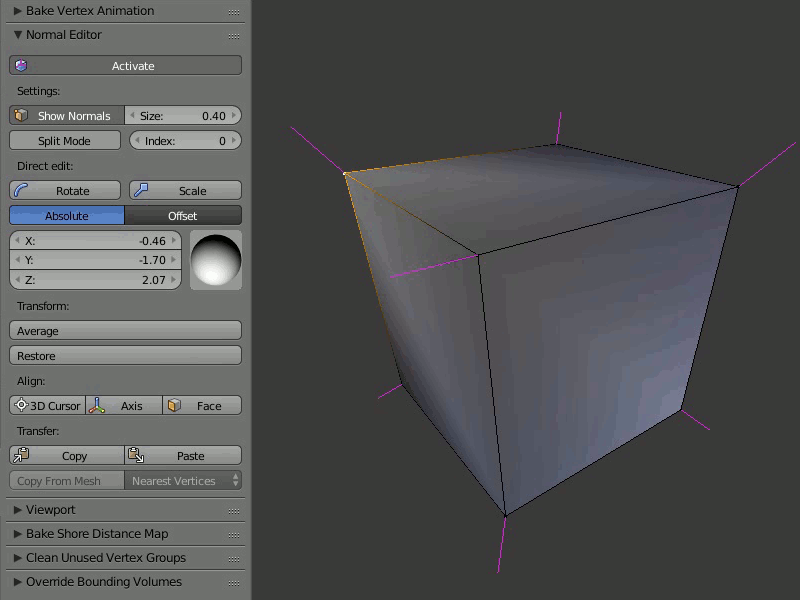
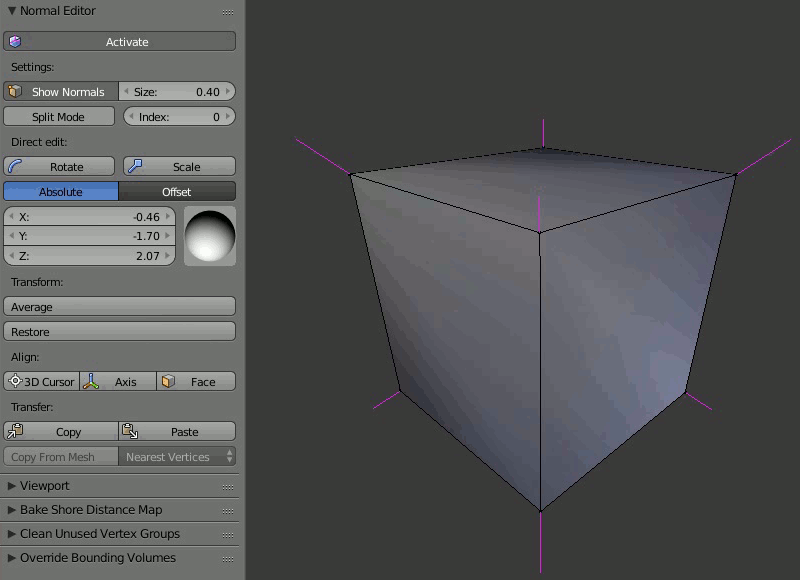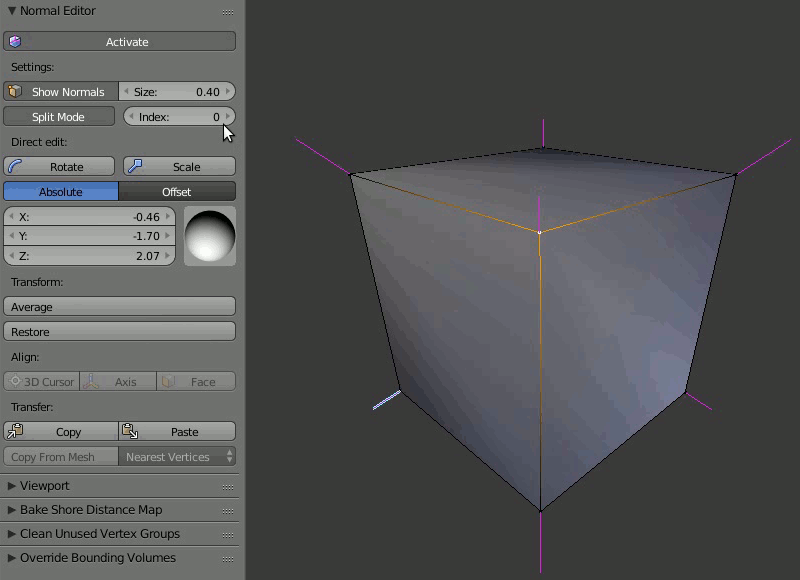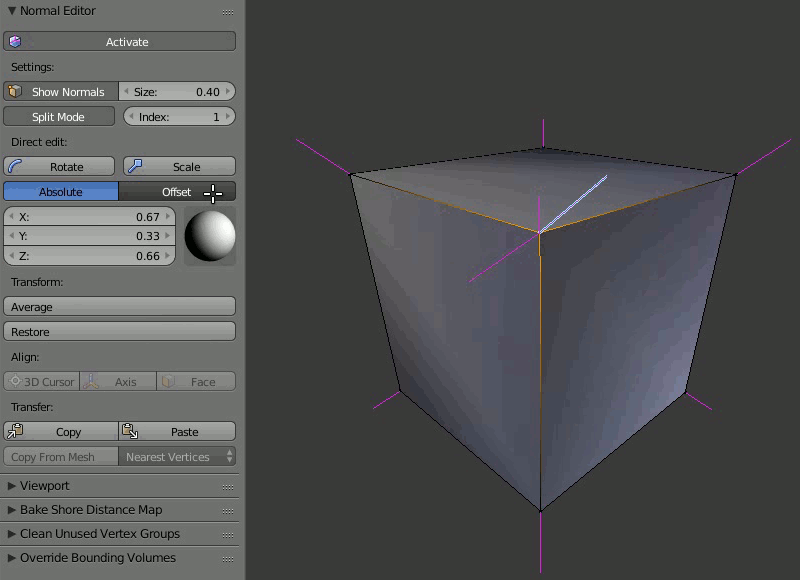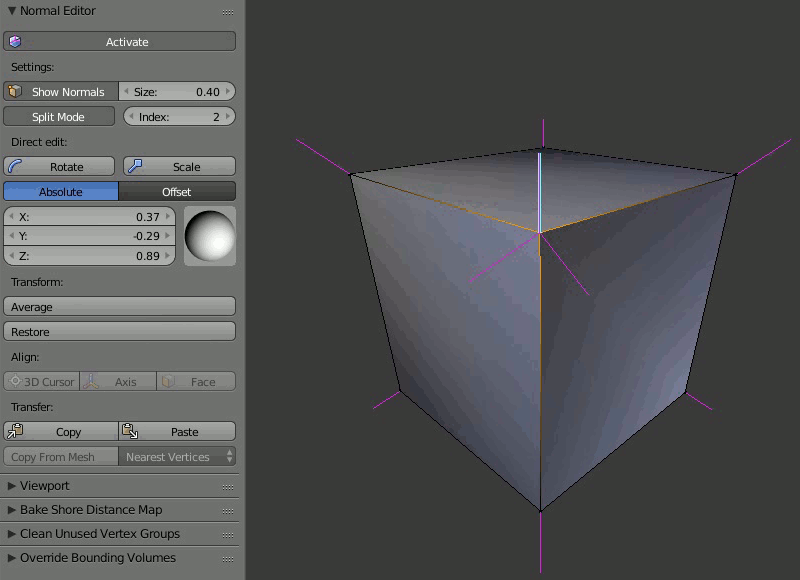
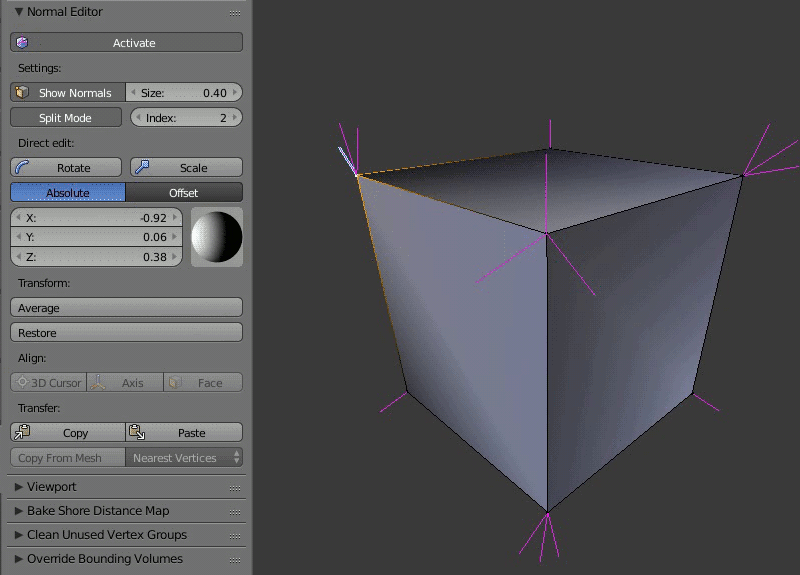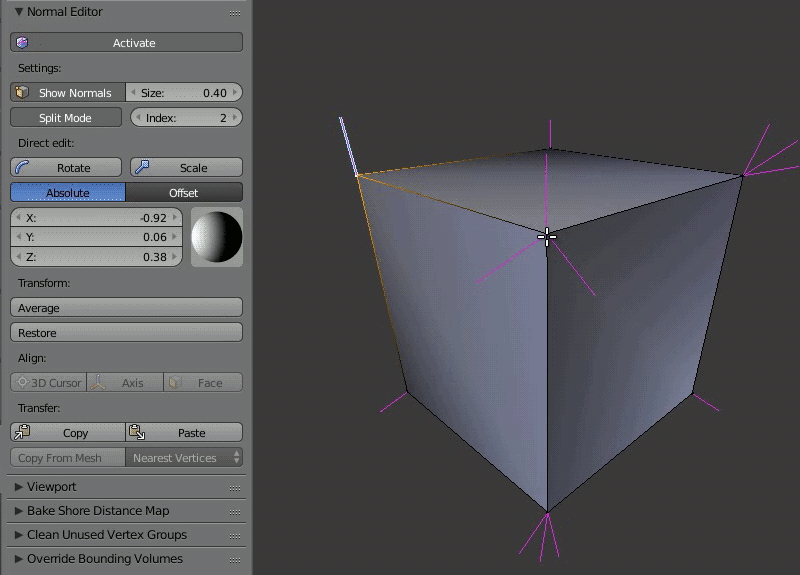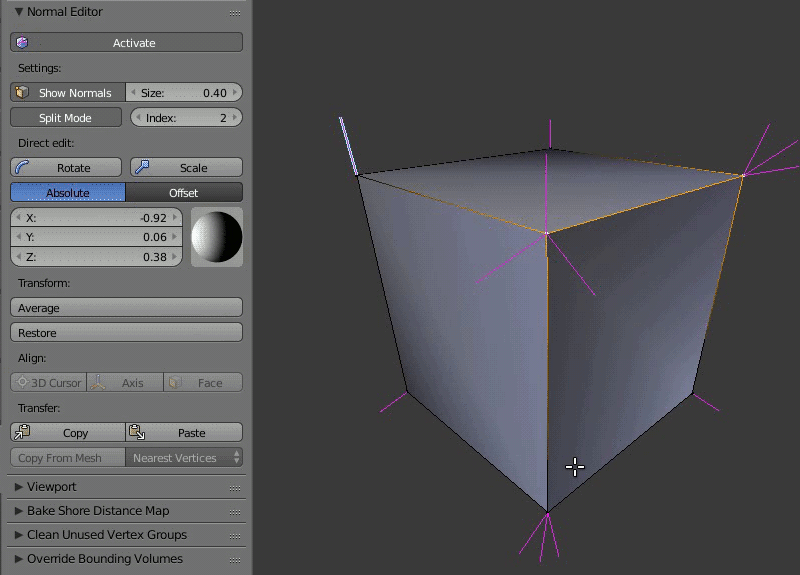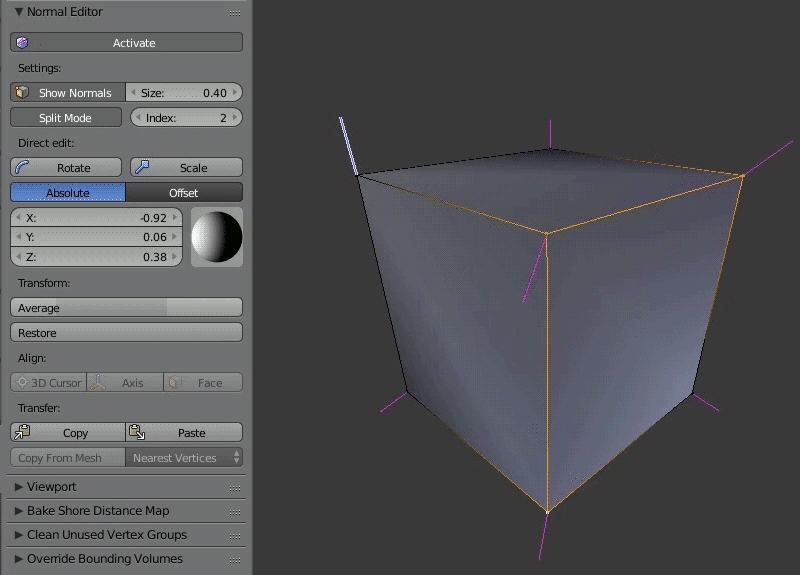
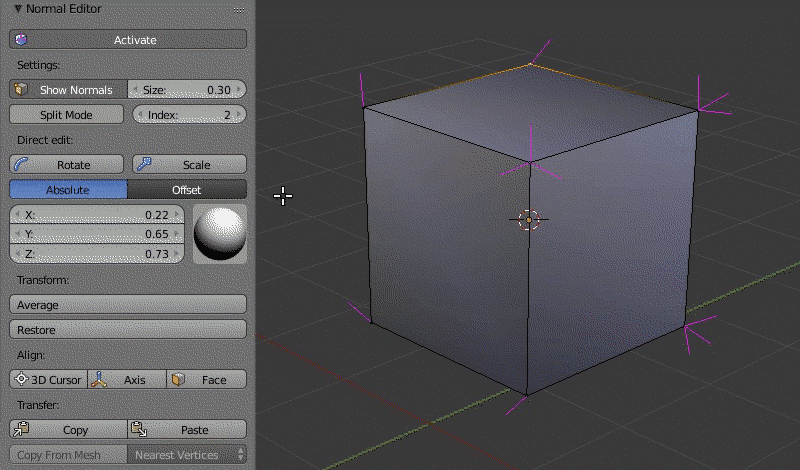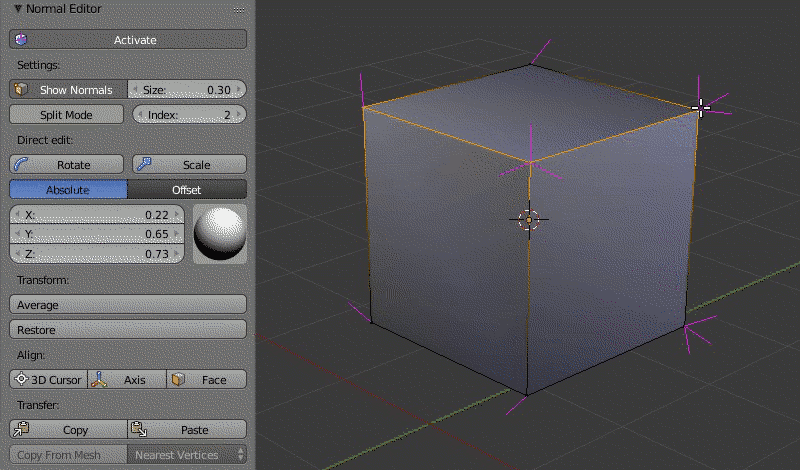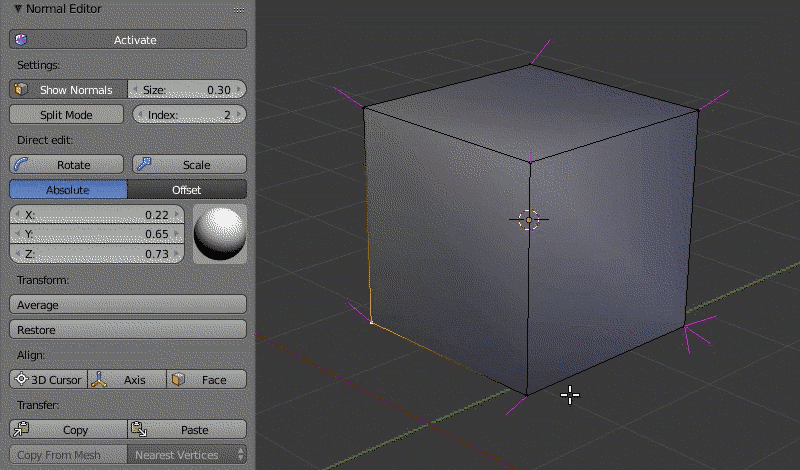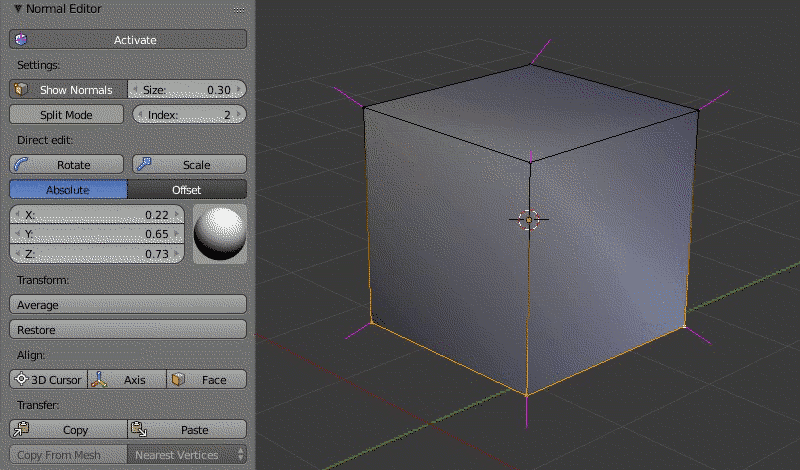
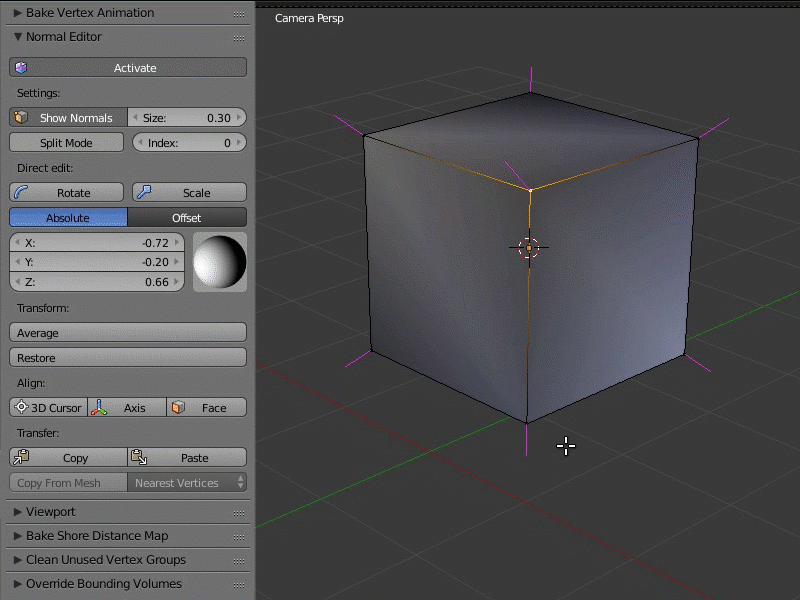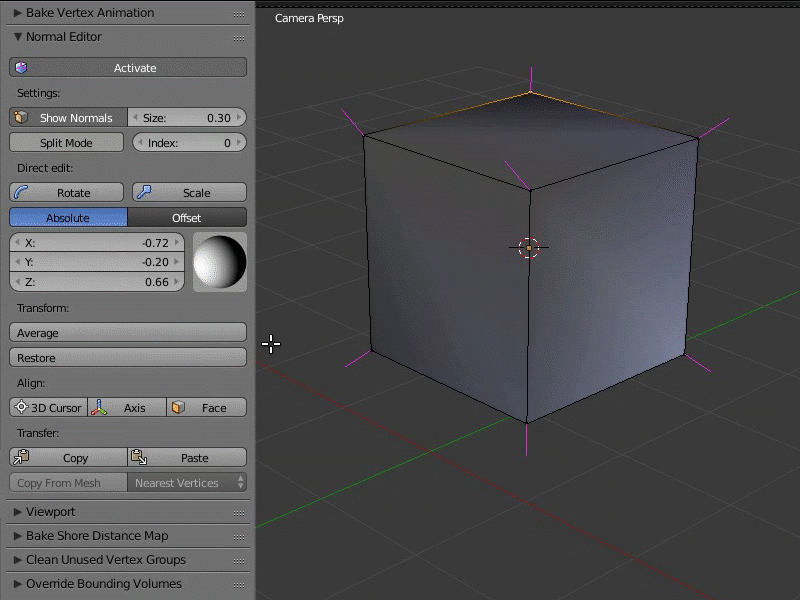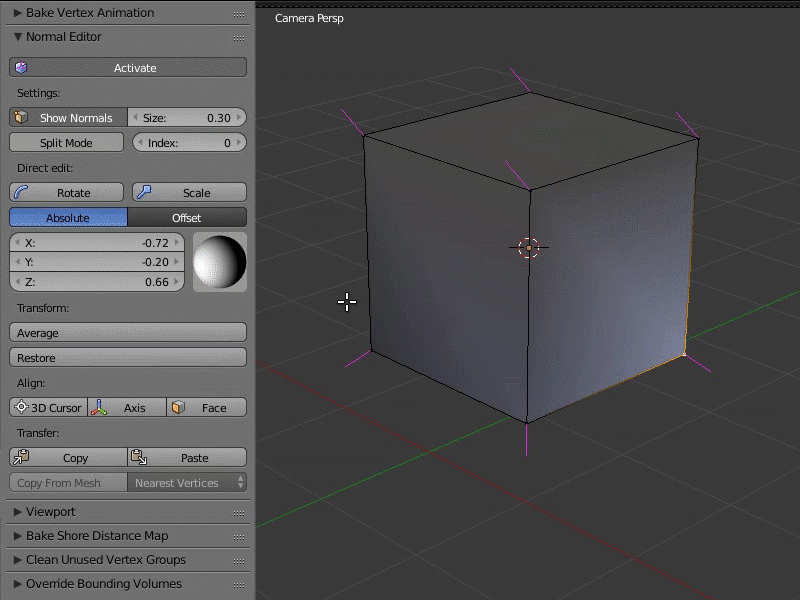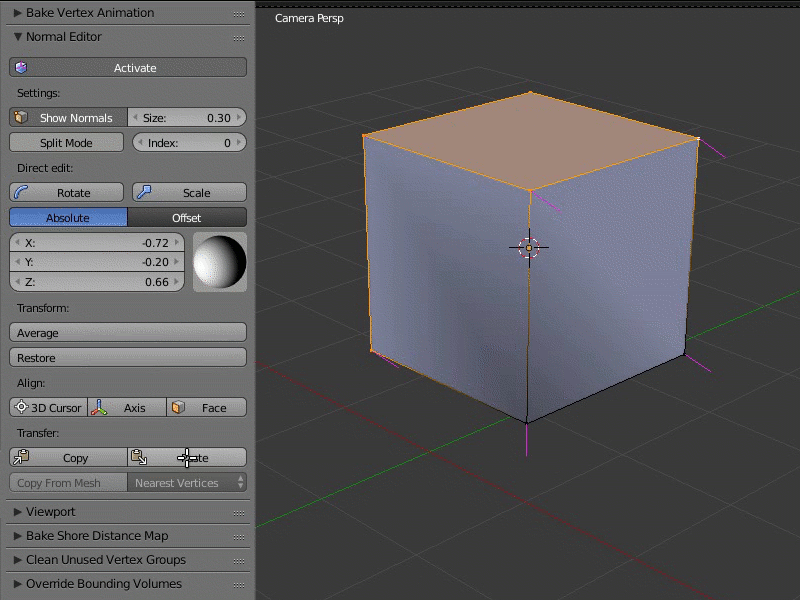
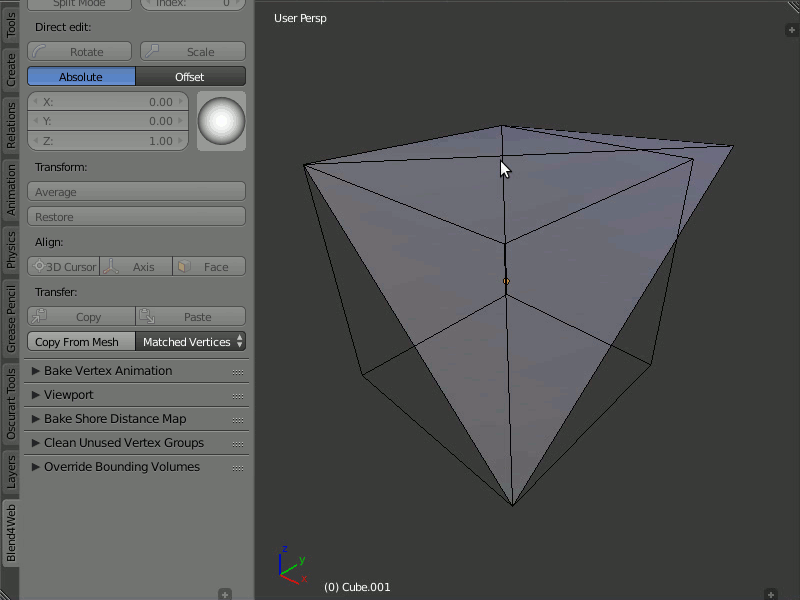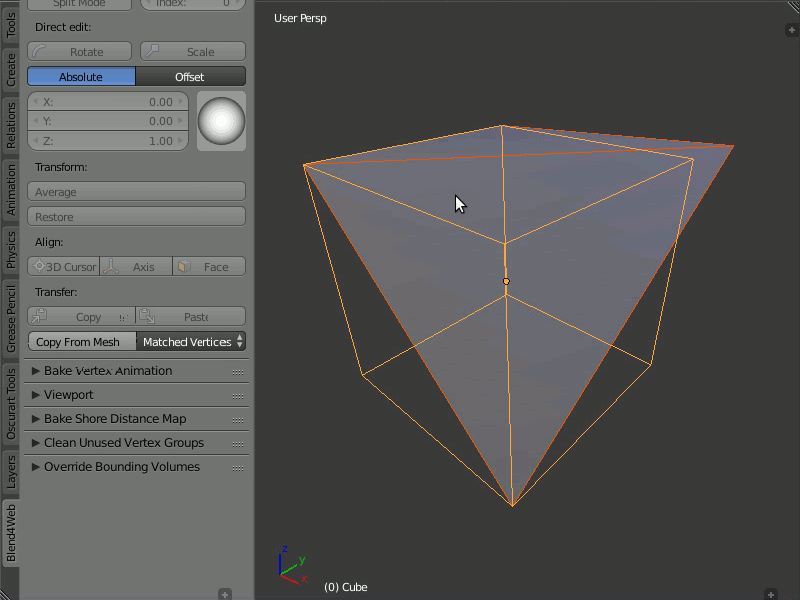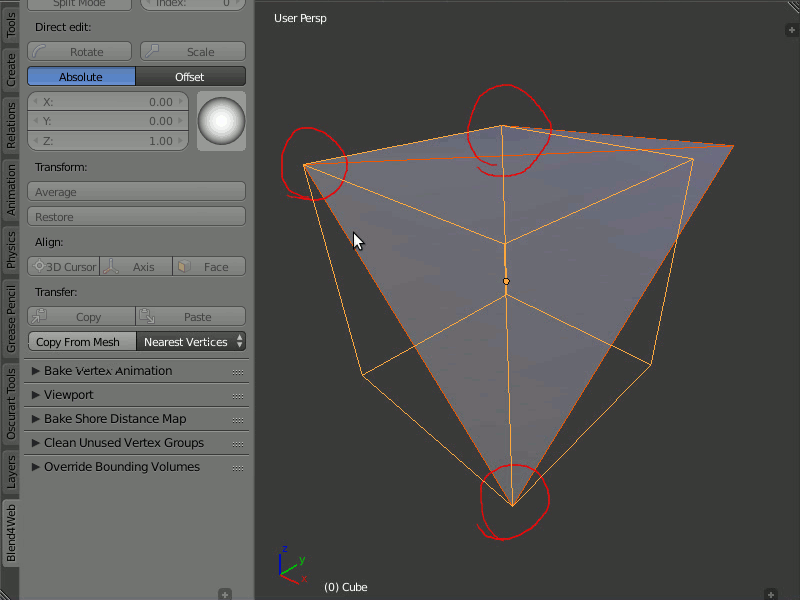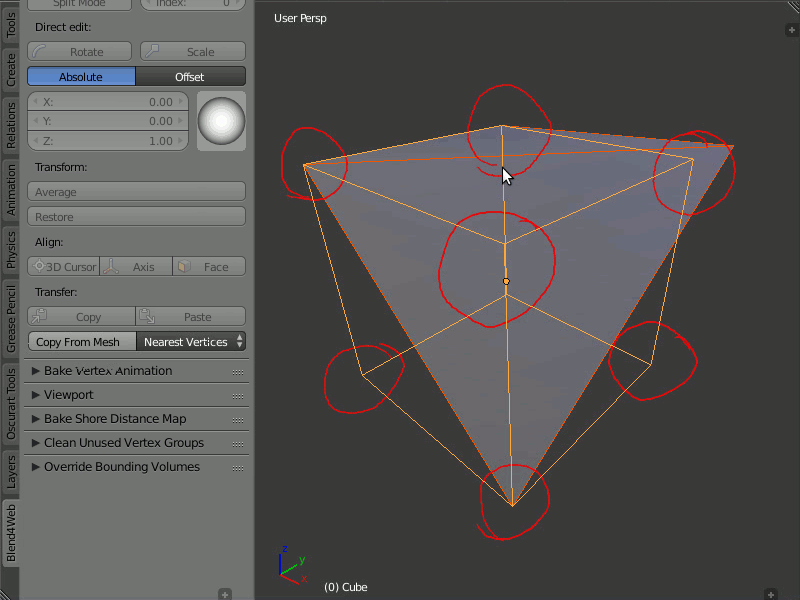
Пример работы редактора нормалей:

Основные особенности редактора нормалей:¶

для хранилища массива данных с направлениями вертексных нормалей используется “родной” блок данных Blender (появился в версии 2.74);

редактирование нормалей и отображение затенения теперь происходит в режиме редактирования ( Edit Mode );

все изменения записываются сразу же автоматически;

редактированные нормали экспортируются автоматически.

Интерфейс¶

Activate¶

Кнопка Activate включает режим редактирования вертекных нормалей.

Show Normals¶

Для удобства в панель продублирована оригинальная кнопка Blender, включающая отображение маркеров вертексных нормалей во Viewport’е, а так же настройка их длины.

Rotate¶

При помощи этого инструментария можно вращать нормаль каждого вертекса индивидуально. Функция Rotate также доступна по горячим клавишам Shift+Ctrl+R и позволяет вращать вертексные нормали в привычном для пользователя Blender режиме.

Выделив один или несколько вертексов, которые хотите изменить, вращайте их, используя визуальную сферу на панели редактора вертексных нормалей Blend4Web, или задайте направление каждой координате в цифровом значении.

Scale¶

Обратите внимание, что видимая длинна нормали определяется параметром Size и не меняется при масштабировании.

Режимы Absolute и Offset¶

Режим Absolute¶

Режим Offset¶

В этом режиме к нормальному вектору прибавляется вектор, заданный пользователем.

Split Normals¶

Режим Split Normals позволяет редактировать вертексные нормали индивидуально для каждой грани ( Face в Blender), образующей редактируемую вершину ( Vertex в Blender). Переключатель вертексных индексов позволяет перемещаться между нормалями разделенного вертекса.

Average¶

Restore¶

Кнопка Restore восстанавливает исходное направление нормалей выделенных вертексов.

3D Cursor, Axis и Face¶

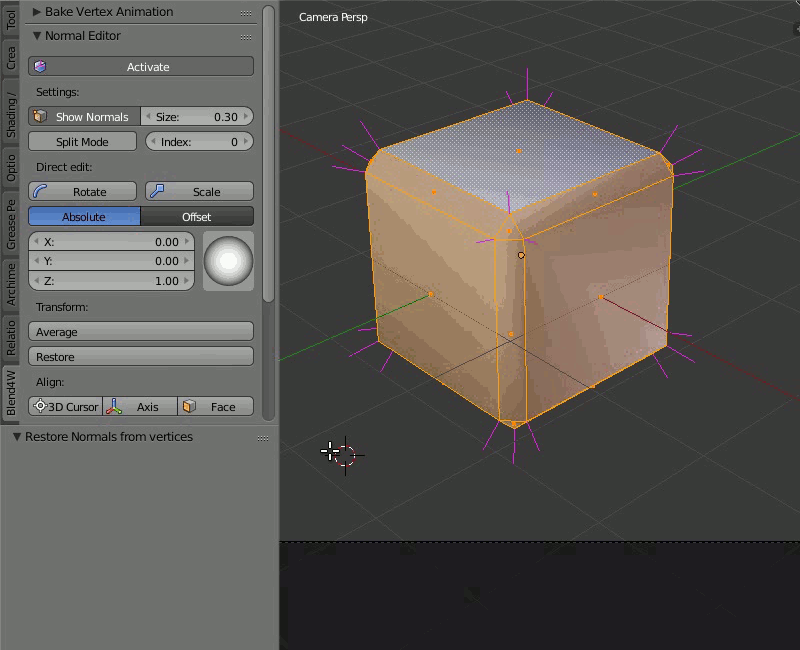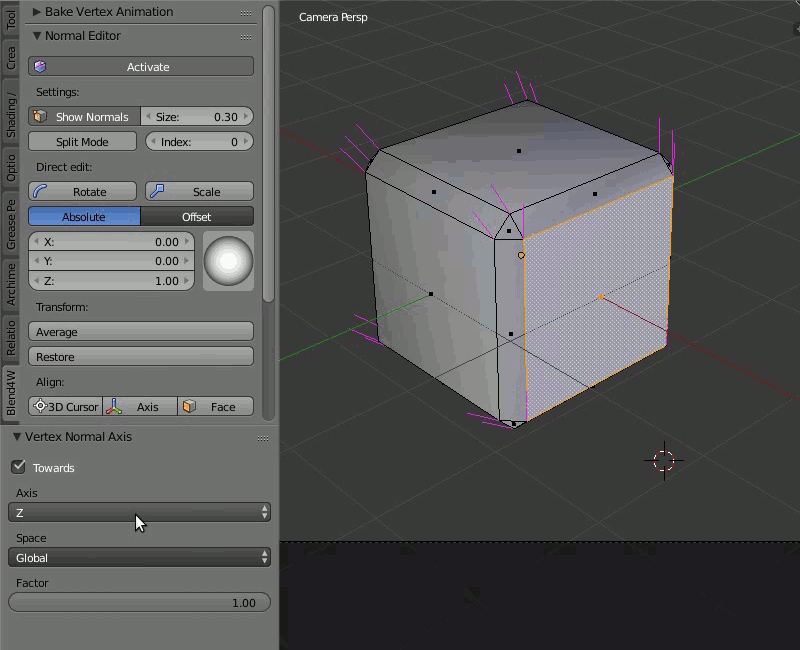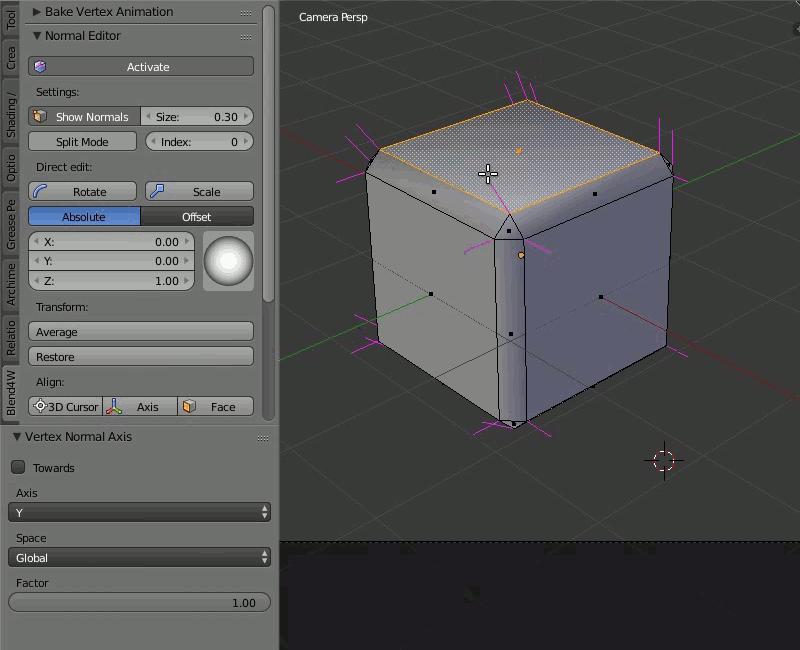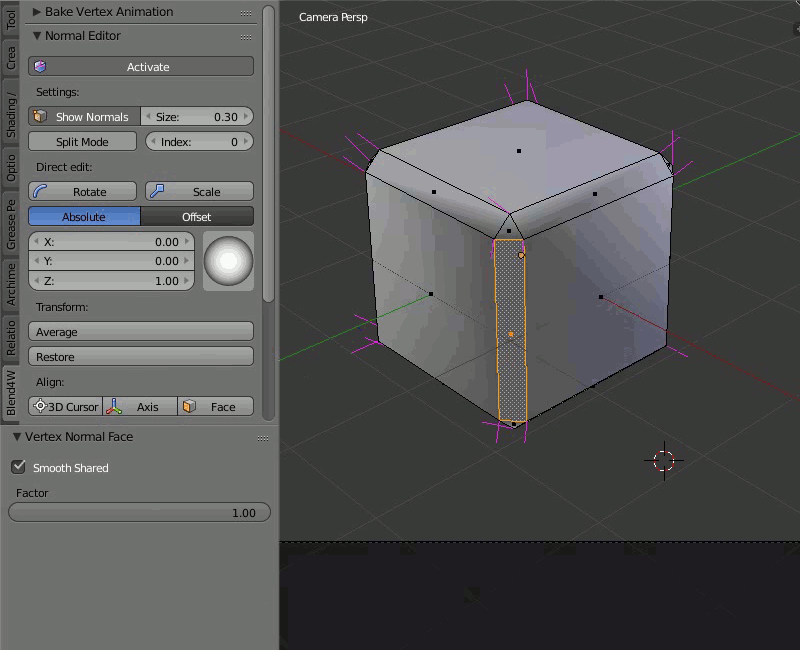
Кнопка 3D Cursor ориентирует нормали выбранных вершин по направлению к 3D-курсору (если активирован параметр Towards на панели Vertex Normal Cursor ) или в противоположную сторону. Кнопка Axis направляет нормали вдоль одной из осей координат (ось задаётся на той же панели Vertex Normal Cursor ). Кнопка Face ориентирует нормали всех вершин выбранной грани параллельно нормали этой грани.

Использовать функцию Axis очень просто: достаточно выбрать вершины и нажать кнопку, после чего функция направит нормали этих вершин вдоль оси координат, выбранной на панели Vertex Normal Cursor (по умолчанию выбрана ось Z) или в противоположном направлении (если отключить опцию Towards на той же панели).

Copy/Paste¶

Копирует направление нормали с одного вертекса на другой.

Copy From Mesh¶

В режиме Matched Vertices копируются направления нормалей с вертекса одной модели на вертекс другой, если у них одинаковые координаты; прочие вертексы игнорируются. В режиме Nearest Vertices копируются нормали с ближайших вертексов другой модели.

Работа с этой функцией производится в объектном режиме. Первым нужно выделить объект, с которого будет происходить копирование, далее объект, на который будет происходить копирование. Необходимо также выделить вертексы целевого объекта, на которые необходимо произвести перенос направления нормалей.

© Copyright 2014-2017, Триумф. Обновлено: 2019-04-16.

Источник

Простой Blender. Часть 3

КДПВ 3. Неполная разборка

В предыдущей части я писал об объектах. Эта часть — о геометрии.

Геометрия

По традиции, отступление

Как бы я ни хотел сделать пост поменьше (а картинок — побольше), такая серьезная тема как геометрия все-таки требует понимания.
Не понимая основ компьютерной графики, в 3D моделировании многого не достичь (разве что скульптингом заняться, но там уже творчество). Поэтому чуть ниже я возьму совсем уж менторский тон, одновременно погружаясь в пучины основ. Если вы знаете, чем треугольник отличается от полигона, а тот — от нормали, то смело и решительно пропускайте.

В компьютерном представлении 3х-мерный объект обычно представляется как набор точек с координатами, ребер между ними и граней, которые натянуты на эти ребра.
“Обычно” — потому что есть еще как минимум воксели.

Подробнее.
Точка (vertex) — это базис и основа, это альфа и омега, без точек — никак. Точки могут и существуют сами по себе. Характеристика точки — координаты.
Ребро (edge) — это соединение ровно двух точек. По-русски это “трехмерный отрезок”. Характеристики ребра — точки, его образующие и, собственно, сама линия.

Итак, ребра создают каркас. На этот каркас потом натягивается то, ради чего и затевается обычно (необычность) весь этот балет — грани. Или полигоны. Или поверхности. Я возьму на себя смелость использовать далее свои термины — просто потому, что мне так удобней.

Итак. Поверхность (полигон, грань) натягивается на замкнутую “рамку” из ребер. Минимальное возможное количество ребер в рамке равно трем, что очевидно, иначе это уже будет палка.
Теперь главный поинт: треугольник из 3 ребер нельзя изогнуть. Это важно. У него все ребра всегда лежат в одной плоскости. Если потянуть за любую из его вершин (точек, которым принадлежат его ребра), то поверхность не переломится. Это свойство критично для компьютерных расчетов, поэтому, в принципе, после точки и ребра идет:

Треугольник — поверхность, натянутая на замкнутую рамку из 3 ребер. Характеристики: ребра, координаты вершин, и нормаль. Нормаль — это чисто компьютерная характеристика, нужная для расчета освещения. Если вы никогда не собираетесь рендерить свои модели, либо экспортировать в другую программу, то забудьте про нормаль. Если собираетсь, то вот объяснение. У треугольника есть 2 поверхности. Когда мы говорим, что свет падает на поверхность треугольника, то нужно указать (этого требуют алгоритмы расчета), с какой стороны ожидается, что он будет падать, другими словами, указать внешнюю сторону треугольника. Нормаль — это вектор, выходящий из треугольника под прямым углом к его поверхности во внешнюю сторону. Некоторые программы (не Blender) просто не отрисовывают внутреннюю сторону треугольника, могут быть дырки. У точки и ребра поверхностей нет, поэтому и нормали у них тоже нет.

Рисунок 1. Треугольник (серый) с выходящей из него нормалью (голубая линия). Как видим, внешняя сторона у этого треугольника — вверху и нам не видна. Есть программы, которые не рендерят треугольники, если внешняя сторона не видна из камеры. На рендере из такой программы на месте изображенного треугольника было бы то, что находится за ним.

Этим, в принципе можно было бы и ограничиться, так как треугольника достаточно, чтобы замостить любую поверхность с достаточно хорошим приближением. Слово “достаточно” тут ключевое. Чем больше треугольников — тем больше нагрузка на систему. Процесс стартового замощения треугольниками называется триангуляцией. Процесс увеличения детализации уже триангулированной поверхности — это тесселяция. Видеокарточки, OpenGL, DirectX оперируют именно треугольниками. Принцип минимальной необходимости.

Однако, когда мы говорим о моделлинге, в свои права вступает человеческая лень. Если мне скажут триангулировать рамку, показанную на рисунке 2, то я это сделаю. А если мне скажут, что есть алгоритмы автоматической триангуляции, то я попробую автоматизировать процесс. Такие алгоритмы есть. Поэтому появляется следующая ступень — полигон.

Полигон — набор треугольников, лежащих в одной плоскости и соприкасающихся друг с другом ребрами.

Рисунок 2. Слева — замкнутая рамка из ребер, по центру — ее триангуляция (лично сделал!), справа — полигон на этой рамке.

Состыковывая между собой треугольники (или полигоны), лежащие в разных плоскостях мы и получаем то, что называется “объект”.

Важно понимать, что, например, у понятия “точка” есть свои обязательные атрибуты — координаты, а вот у понятия “объект” их нет. Даже замкнутость его поверхности — необязательна. Даже состыковка полигонов — необязательна. Две точки — это объект. Точка — это тоже объект. Если вы, как автор модели, так решили — значит, так и будет в рамках данной модели.

Более того, в 3D редакторах есть объект “Empty” (используется как вспомогательный). У него есть только координаты. Точки нет, а координаты есть.

Резюмируя. Геометрические понятия в 3D моделлинге, начиная снизу: точка, ребро, треугольник (и производная — полигон). А вот объект — это просто контейнер для геометрических элементов.

Рисунок 3. Молекулярная, так сказать, модель объекта. Данный объект состоит из 8 точек (одна не привязана ни к чему), 9 ребер, треугольника (не подписан на английском намеренно) и полигона (рассчитан автоматически, на самом деле состоит из двух треугольников).

Вынырнув из пучин основ, теперь я нырну в пучины рассуждений. Эта часть тоже необязательная, но поможет лучше понять мою позицию.

Примитивы

В прошлой серии я писал о примитивах. “Примитив” — это, по большому счету, маркетологический термин. Назвать Сюзанну примитивной я не могу. На самом деле, примитивы следовало бы назвать “базовые объекты” или “стандартные объекты” — ну как-то так. Но, спорить об устоявшихся терминах — дело неблагодарное. Примитив так примитив.

Так вот, примитивы, как вы уже поняли — это не самое дно (я в хорошем смысле этого слова) моделирования. Самое дно моделирования — это, как вы уже поняли — точки, ребра и грани, из которых они состоят. Как и любой другой 3D объект.

В примитивах нет ничего особенного. Они доступны сходу просто потому, что они общеупотребимы и имеют простую форму, что помогает применить технику Микеланджело — посмотреть на моделируемый объект, прикинуть наиболее похожий примитив, создать его и отсечь лишнее. Причем от программы к программе набор примитивов разнится. В максе есть даже “расширенные примитивы” (помимо обычных), включающие в себя уголок, цилиндр с фасками, капсулу, узел и т.п.

Для повышения удобства пользования у примитивов выделили присущие им ключевые параметры (например, радиус у шара) и дали возможность эти параметры при старте задавать. После задания параметров и подтверждения создания 3D-пакет согласно соответствующему скрипту просто расставляет точки, натягивает ребра и треугольники с учетом этих параметров. Вуаля — примитив готов.

Примитивы — это просто библиотека для ускорения работы.

Модификаторы

Как уже ясно, модификаторы работают на уровне геометрии объектов, а не самих объектов. Объект — это просто контейнер. Работу любого модификатора можно проделать на том же уровне геометрии и руками, просто это дольше. Модификаторы — из той же оперы, что полигон и примитивы.

Собственно, разница идеологий

Кнопка “Создать шарик” в Blender делает именно то, о чем я написал выше. Программа создает геометрию. Можно указать точные параметры сферы, но только один раз — при создании. При снятии выделения с шарика параметры заново не укажешь. Blender в этом смысле хардкорен по сравнению с максом, где…

“Создать шарик” в максе — это команда стека. Это процедура. Она помещается в низ стека, выбрав ее в стеке можно переуказать параметры сферы: радиус, количество сегментов и т.п. Она не порождает геометрию (в том смысле слова, что ее можно редактировать), она порождает основу для последующих модификаторов. Макс как бы намекает нам: “Эй, не надо копаться с точками! У меня есть сто миллионов модификаторов и даже расширенные примитивы, просто скомбинируй!” Работа с геометрией в максе — это исключение. Настолько, что был введен модификатор редактируемой геометрии. Вдумайтесь — модификатор, который просто разрешает работать вручную с геометрией. Но все-таки, в максе можно работать с геометрией, так что…

Так что получается, что Blender не так гибок, как макс: не нравится получившаяся детализация — пересоздавай примитив, указывай нужные параметры, заново проделывай те же операции. Мрак. Вроде.

Если в максе сделать шар, применить модификатор “Edit Mesh”, передвинуть парочку вершин/ребер/граней, а затем кликнуть на команду стека “Создать шарик” (ну типа не нравится мне детализация, хочу воспользоваться архитектурным совершенством макса), то произойдет следующее:

Рисунок 4. Макс. Возврат в начало стека после ручной работы с геометрией. Так как макса давно нет под рукой, то выдирал из видео, сорри за качество.

Макс перекладывает ответственность на юзера, ведь чудес не бывает: если я передвинул два рядом стоящих полигона в противоположные стороны, а потом в стеке уменьшил детализацию сферы в 4 раза — при подъеме вверх по стеку куда двигать полигон, находящийся на месте предыдущих двух?

Рисунок 5. Дилемма выбора макса. Сдвинули один полигон влево, другой — вправо, потом откатились к старту стека и уменьшили детализацию. Куда двигать полигон?

Фактически, стек макса тут бессилен и фактически же параметры сферы в максе тоже задаются раз и навсегда. Все вышесказанное справедливо, если мы говорим о ручной работе с геометрией (которая включает в себя развертку). Если речь идет только модификаторах, то тут макс в своем праве.

Зато в максе есть align to, а вот Blender все филонит (аддоны нещитово).

Резюмируя: макс рассчитывает на то, что вы начинаете работу с концепции примитива и будете оперировать модификаторами, а в Blender — с геометрии примитива и будете оперировать с геометрией (но модификаторы тоже есть).

Работа с геометрией

Точка поворота

Как я уже написал выше, объект в Blender — это контейнер. У него, помимо собственно геометрии (mesh), есть также название, стек модификаторов, материалы примененные, и origin — точка поворота. Устанавливается она по умолчанию в центр масс примитива, но ее можно передвинуть (либо она сама уедет, оказавшись не там, где надо — ниже приведен пример). Для установки origin надо выделить объект и, не снимая выделения, поставить 3D курсор в нужном месте и нажать Shift-Ctrl-Alt-C (или пробел — Set origin, если кому пальцев жалко).
Ниже иллюстрации.

Рисунок 6. Слева куб с точкой поворота (грязно оранжевый квадратик), выставленной по умолчанию в центр масс. Справа — результат базовой операция поворота куба (специально включил отображение контроллеров для наглядности) — куб крутится на месте.

Рисунок 7. Слева куб со смещенной точкой поворота (я создал куб в центре координат, сдвинул его в сторону, нажал Shift-S, выбрал Cursor to Center, а затем Shift-Ctrl-Alt-C и выбрал “Origin to 3D cursor”). Справа — результат базовой операция поворота куба (специально включил отображение контроллеров для наглядности) — куб крутится не на месте, а по кругу.

В первой серии я упоминал, что Blender фокусируется на задачах, отбрасывая ненужное в данный момент. Помимо лэйаутов, это относится еще и к такой концепции, как “режим работы”.

Вот его индикатор — выпадающий список с почти всеми доступными режимами:

Рисунок 8. Возможные режимы работы Blender (есть еще режим установки позы, но он доступен только при выборе кости). При переключении обратите внимание, на то, как меняются ближайшие к индикатору пункты меню в зависимости от режима работы.

До текущего момента мы работали в Object Mode. В нем минимальной единицей работы является объект. Максимальной — вся сцена.

Для работы с геометрией надо а) выбрать интересующий объект и б) перейти в Edit Mode. Горячая клавиша переключения между именно Object и Edit Mode — клавиша Tab (напоминаю, должен быть выделен объект). Можно, естественно, воспользоваться и выпадающим списком режимов. Далее режим работы с геометрией я буду называть EM — сокращенно от Edit Mode. Режим работы с объектами, соответственно — OM.

Минимальная единица работы в EM — точка. Максимальная — вся геометрия объекта.

Итак, создаем примитив, нажимаем Tab и видим следующее:

Рисунок 9. Отображение объекта для работы на уровне геометрии.

Вся геометрия выделена потому, что вы только что создали примитив в OM и потом перешли в EM. Blender не знает, с чем именно вы хотите работать и предлагает работать со всей геометрией сразу (мог бы вообще не предлагать, но в BF сидят дружелюбные люди). Если вы прямо сейчас потянете за контроллер и сдвинете всю геометрию вправо, то увидите, как геоетрия уехала, а вот origin остался на месте. Сдвиньте и вернитесь в OM, а затем поверните кубик. Вот поэтому я писал об origin. И вот поэтому EM — это режим работы именно с геометрией. Origin — это не геометрия объекта, это отдельная характеристика объекта.

В этом месте уместно сказать, что на уровне сцены Blender оперирует именно и только объектами и их сочетаниями. Нельзя просто так взять и создать геометрию без объекта — у нее не будет ни origin, ни имени, ни всего остального. А если попытаться дать геометрии имя — так ведь это опять объект получается. Геометрия — это важная часть объекта, но только часть, это критично.

Итак, как выделить нужный элемент (пару точек или ребро, например)? Очень просто. Сначала нужно сказать Blender, какой тип геометрии вас интересует. Можно через UI:

Рисунок 10. Кнопки 1 переключают между точками, ребрами и гранями, кнопка 2 включает/выключает бэкфейсинг (учет элементов на задней поверхности объекта).

А можно в EM нажать Ctrl-Tab:

Рисунок 11. Меню выбора способа работы с геометрией. Работает курсор, мышь и даже кнопки 1,2,3.

Оперирование геометрией

Blender, в отличие от макса, не дает оперировать таким понятием, как треугольник. Он оперирует полигоном. И он сам его режет на треугольники. Если вам нужен тотальный контроль — делайте все полигоны треугольными. Рисунок 3 отображает эти реалии — в Blender доступны те элементы, у которых на рисунке есть английское название.

Выбор элемента

EM-only

Вообще, так как в любой мало-мальски нетривиальной геометрии ОЧЕНЬ много элементов, то и способов выбора в EM тоже гораздо больше, чем в OM. Все я перечислять не буду — проще заглянуть в Select (переключившись в EM), там есть режимы выделения, которые относятся только к геометрии. Используются редко, но порой очень выручают.

Базовые операции над элементами

Перенос, поворот, масштабирование работает так же, как и в OM.
Upd. Leopotam (взявший на себя роль строгого редактора моих опусов, за что ему спасибо) заметил, что origin — это только одна из возможных точек поворота. Доступны и другие, выбор можно сделать здесь:

Оперирование элементами

Опять же, геометрия — это, прежде всего, множество связанных(!) элементов. И возможных операций для них побольше, чем для объектов. Например, операция Subdivide (делит элемент на указанное количество частей). Основные операции отображены в панели по T. Все — в меню Mesh. Некоторые из них — контекстно-зависимы, учитывайте это (Subdivide бессмысленен для точки. Да и для объекта тоже — как разделить на равные части несимметричный объект?).

При вызове операции внизу в панели детальной настройки можно указать параметры операции.

Укажу здесь самые часто используемые мной операции:

Причина появления случайных дублей — остальные незавершенные операции можно откатить по Esc. Экструзия же — это 2 операции — создание геометрии и собственно ее перенос. По Esc отменяется только перенос, геометрия остается. Чтобы удалить ее — надо нажать Ctrl-Z.

Хочу отдельно обратить внимание на то, что в EM доступно создание примитивов. При создании к текущей геометрии объекта добавится геометрия (и только) вновь созданного примитива.

Работа с нормалью

Также, при работе с геометрией порой возникают проблемы с нормалями. Чтобы понять текущую ситуацию, вам нужно будет просматривать нормали:

Рисунок 12. UI отображения нормалей. Слева — кнопки способа отображения, справа — длина вектора (в случае с хитрой геометрией помогает, если выкрутить на максимум — посмотреть, где пробьется).

И управлять ими — вкладка «Shading/UVs» (что логично, так как нормали нужны для освещения) панели по T.

Заключение

Используя вышеописанные приемы, можно за полминуты сделать такой же объект, как и на рисунке 3. Можете потренироваться. Операция удаления требует а) выделить удаляемое и б) нажать Delete (в случае геометрии вас могут спросить, что удалять. Если нужно удалить полигон, не трогая его ребра или же ребро, не трогая его точки — выбирайте вариант, где есть слово only):

Рисунок 13. Пример объекта.

Источник

NormalsпѓЃ

The Normal Edit Modifier can be used to edit normals.

The Weighted Normal Modifier can be used to affect normals by various methods, including Face Strength (see below).

You can also copy normals from another mesh using Mesh Data Transfer ( operator or modifier ).

FlipпѓЃ

Mesh ‣ Normals ‣ Flip

This will reverse the normals direction of all selected faces. Note that this allows you to precisely control the direction (not the orientation, which is always perpendicular to the face) of your normals, as only the selected faces are flipped.

RecalculateпѓЃ

Mesh ‣ Normals ‣ Recalculate Outside and Mesh ‣ Normals ‣ Recalculate Inside

These tools will recalculate the normals of selected faces so that they point outside (respectively inside) the volume that the face belongs to. The volume does not need to be closed; inside and outside are determined by the angles with adjacent faces. This means that the face of interest must be adjacent to at least one non-coplanar other face. For example, with a Grid primitive, recalculating normals does not have a meaningful result.

Set from FacesпѓЃ

Mesh ‣ Normals ‣ Set from Faces

Set the custom normals at corners to be the same as the face normal that the corner is part of.

RotateпѓЃ

Mesh ‣ Normals ‣ Rotate

Point to TargetпѓЃ

Mesh ‣ Normals ‣ Point to Target

A target is set by the keys:

The mouse cursor M

The object origin O

The tool operation can be modified; if one of the following keys has been previously pressed:

All normals will point in the same direction: from the center of selected points to the target.

Each normal will be an interpolation between its original value and the direction to the target.

The normal directions are reversed from what was specified above.

Will reset the custom normals back to what they were when the operation started.

MergeпѓЃ

Mesh ‣ Normals ‣ Merge

Merge all of the normals at selected vertices, making one average normal for all of the faces.

SplitпѓЃ

Mesh ‣ Normals ‣ Split

Split the normals at all selected vertices so that there are separate normals for each face, pointing in the same direction as those faces.

AverageпѓЃ

Mesh ‣ Normals ‣ Average

Average all of the normals in each fan of faces between sharp edges at a vertex.

Copy VectorsпѓЃ

Mesh ‣ Normals ‣ Copy Vectors

If a single normal is selected, copy it to an internal vector buffer.

Paste VectorsпѓЃ

Mesh ‣ Normals ‣ Paste Vectors

Replace the selected normals with the one in the internal vector buffer.

Smooth VectorsпѓЃ

Mesh ‣ Normals ‣ Smooth Vectors

Adjust the normals to bring them closer to their adjacent vertex normals.

Reset VectorsпѓЃ

Mesh ‣ Normals ‣ Reset Vectors

Put normals back the to default calculation of the normals.

Select by Face StrengthпѓЃ

Mesh ‣ Normals ‣ Select by Face Strength

Another way to affect normals is to set a Face Strength on the faces of the model. The Face Strength can be either Weak, Medium, or Strong. The idea is that the Weighted Normal Modifier can be set to pay attention to the Face Strength as follows: When combining the normals that meet at a vertex, only the faces with the strongest Face Strength will contribute to the final value.

For example, if three faces meet at a vertex and have the face weights weak, medium, and strong, then only the normal associated with the strong face will be used to set the final result.

Use the submenu to pick one of Weak, Medium, or Strong. Then this tool selects those faces that have the chosen face strength.

Set Face StrengthпѓЃ

Mesh ‣ Normals ‣ Set Face Strength

Use the submenu to pick one of Weak, Medium, or Strong. Then this tool changes the Face Strength of currently selected faces to the chosen face strength.

© Copyright : This page is licensed under a CC-BY-SA 4.0 Int. License. Last updated on 12/13/2021.

Источник