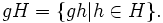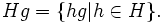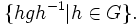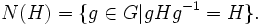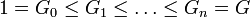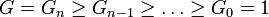Что такое нормальная подгруппа

Минимальная нормальная подгруппа

Минимальная нормальная подгруппа — неединичная нормальная подгруппа , такая, что между ней и единичной подгруппой нет других нормальных подгрупп всей группы.

Минимальная нормальная подгруппа имеются далеко не во всякой группе. Если группа конечна, то любая её минимальная нормальная подгруппа является прямым произведением изоморфных простых групп. Если минимальная нормальная подгруппа у группы существует и единственна, то она называется монолитом (иногда сердцевиной), а сама группа называется монолитичной.

Полезное

Смотреть что такое «Минимальная нормальная подгруппа» в других словарях:

МИНИМАЛЬНАЯ НОРМАЛЬНАЯ ПОДГРУППА — неединичная нормальная подгруппа Нтакая, что между ней и единичной подгруппой нет других нормальных подгрупп всей группы. М. н. п. имеются далеко не во всякой группе. Если группа конечна, то любая ее М. н. п. является прямым произведением… … Математическая энциклопедия

Глоссарий теории групп — Группа (математика) Теория групп … Википедия

Словарь терминов теории групп — Для общего ознакомления с теорией групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И К Л М Н О П Р … Википедия

Изоморфизм групп — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия

Изоморфные группы — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия

Класс смежности — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия

Класс сопряженности — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия

Класс сопряжённости — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия

Конечно определенная группа — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия

Конечно определённая группа — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия

Источник

Нормальный ряд

Для общего описания теории групп см. Группа (математика) и Теория групп.

Курсив обозначает ссылку на этот словарь.

p-группа — группа, все элементы в которой имеют порядок, равный некоторой степени простого числа p (не обязательно одинаковой у всех элементов). Также говорят о примарной группе. Более подробно см. в статье конечная p-группа.

Аддитивная группа кольца ― группа, элементами которой являются все элементы данного кольца, а операция совпадает с операцией сложения в кольце.

Антигомоморфизм групп — отображение групп f : (G,*) → (H,×) такое, что

для произвольных a и b в G (сравните с гомоморфизмом).

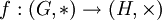
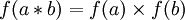
Гомоморфизм групп — отображение групп такое, что

для произвольных a и b в G.

Группа Шмидта — это ненильпотентная группа, все собственные подгруппы которой нильпотентны.

Группа Миллера — Морено — это неабелева группа, все собственные подгруппы которой абелевы.

Групповая алгебра группы G над полем K — это векторное пространство над K, образующими которого являются элементы G, а умножение образующих соответсвует умножению элементов G.

Длина ряда подгрупп — число n в определении ряда подгрупп.

Изоморфизм групп — биективный гомоморфизм.

Изоморфные группы — группы, между которыми существует хотя бы один изоморфизм.

Индекс подгруппы H в группе G — число смежных классов в каждом (правом или левом) из разложений группы G по этой подгруппе H.

Индексы ряда подгрупп — индексы | G_{i + 1}:G_i | в определении субнормального ряда подгрупп.

Класс смежности/смежный класс (левый или правый) подгруппы H в G. Левый класс смежности элемента 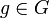по подгруппе H в G есть множество

Аналогично определяется правый класс смежности:

Класс сопряжённости элемента 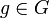есть множество

Коммутант группы есть подгруппа, порождённая всеми коммутаторами группы, обычно обозначается [G,G] или .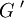

Коммутативная группа. Группа G является коммутативной, или абелевой, если её операция * коммутативна, то есть g*h=h*g .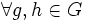

Коммутатор подгрупп — множество всевозможных произведений .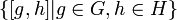

Композиционный ряд группы G — ряд подгрупп, в котором все факторы G_{i + 1} / G_i — простые группы.

Конечная группа — группа с конечным числом элементов.

Конечно определённая группа — группа, обладающая конечным числом образующих и задаваемая в этих образующих конечным числом соотношений.

Конечнопорождённая группа — группа, обладающая конечной системой образующих.

Кручение, TorG, коммутативной или нильпотентной группы G есть подгруппа всех элементов конечного порядка.

Локальная теорема. Говорят, что для некоторого свойства P групп справедлива локальная теорема, если всякая группа, локально обладающая этим свойством, сама обладает им.

Например: локально абелева группа является абелевой, но локально конечная группа может быть бесконечной.

Метабелева группа ― группа, второй коммутант которой тривиален (разрешимая ступени 2).

Метациклическая группа ― группа, обладающая циклической нормальной подгруппой, факторгруппа по которой также циклическая. Всякая конечная группа, порядок которой свободен от квадратов (то есть не делится на квадрат какого-либо числа), является метациклической.

Мультипликативная группа тела ― группа, элементами которой являются все ненулевые элементы данного тела, а операция совпадает с операцией умножения в теле.

Нильпотентная группа — группа, обладающая центральным рядом подгрупп. Минимальная из длин таких рядов называется её классом нильпотентности.

Норма группы — совокупность элементов группы, перестановочных со всеми подгруппами, то есть пересечение нормализаторов всех её подгрупп.

Нормализатор подгруппы H в G — это максимальная подгруппа G, в которой H нормальна. Иначе говоря, нормализатор есть стабилизатор H при действии G на множестве своих подгрупп сопряжениями, то есть

Нормальная подгруппа (инвариантная подгруппа, нормальный делитель). H есть нормальная подгруппа G, если для любого элемента g в G gH = Hg, то есть правые и левые классы смежности H в G совпадают. Иначе говоря, если .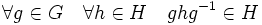

Период группы ― наименьшее общее кратное порядков элементов данной группы.

Периодическая группа ― группа, каждый элемент которой имеет конечный порядок.

Подгруппа — подмножество H группы G, которое является группой относительно операции, определённой в G.

Подгруппа кручения см. кручение.

Для произвольного подмножества S в G, обозначает наименьшую подгруппу G, содержащую S.

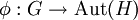
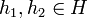
Полупрямое произведение групп G и H над гомоморфизмом (обозначается по разному, в том числе G ⋊_φ H) — множество G × H, наделенное операцией *, для которой (g₁,h₁) * (g₂,h₂) = (g₁φ(h₁)(g₂),h₁h₂) для любых , .

Порядок группы (G,*) — мощность G (то есть число её элементов).

Порядок элемента g группы G — минимальное натуральное число m такое, что g m = e. В случае, если такого m не существует, считается, что g имеет бесконечный порядок.

Простая группа — группа, в которой нет нормальных подгрупп, кроме тривиальной <e> и всей группы.

Примарная группа — группа, все элементы в которой имеют порядок, равный некоторой степени простого числа p (не обязательно одинаковой у всех элементов). Также говорят о p-группе.

Расширение группы — группа, содержащая данную группу в качестве нормальной подгруппы.

Разрешимая группа — группа, обладающая нормальным рядом подгрупп с абелевыми факторами. Наименьшая из длин таких рядов называется её ступенью разрешимости.

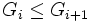
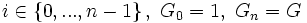
Ряд подгрупп — конечная последовательность подгрупп G₀,G₁. G_n называется рядом подгрупп, если , для всех . Такой ряд записывают в виде

Сверхразрешимая группа — группа, обладающая нормальным рядом подгрупп с циклическими факторами.

Свободная группа, порождённая множеством A — это группа, порождённая элементами этого множества и не имеющая никаких соотношений, кроме соотношений, определяющих группу. Все свободные группы, порождённые равномощными множествами, изоморфны.

Соотношение — тождество, которому удовлетворяют образующие группы (при задании группы образующими и соотношениями).

Факторгруппа группы G по нормальной подгруппе H есть множество классов смежности подгруппы H с умножением, определяемым следующим образом:

Факторы субнормального ряда — фактор-группы G_{i + 1} / G_i в определении субнормального ряда подгрупп.

Холлова подгруппа — подгруппа, порядок которой взаимно прост с её индексом во всей группе.

Центр группы G, обычно обозначается Z(G), определяется как

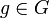
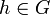
Z(G) = <| gh = hg для любого >,

иначе говоря, это максимальная подгруппа элементов, коммутирующих с каждым элементом G.

Централизатор элемента есть максимальная подгруппа, коммутирующая с этим элементом.

Центральный ряд подгрупп — нормальный ряд подгрупп, в котором 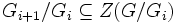, для всех членов ряда.

Циклическая группа — группа, состоящая из порождающего элемента и всех его целых степеней. Конечна в случае, если порядок порождающего элемента конечен.

Ядро гомоморфизма — прообраз нейтрального элемента при гомоморфизме. Ядро всегда есть нормальная подгруппа, более того, любая нормальная подгруппа есть ядро некоторого гомоморфизма.

Литература

Полезное

Смотреть что такое «Нормальный ряд» в других словарях:

НОРМАЛЬНЫЙ РЯД — группы ряд нормальных подгрупп группы (см. Подгрупп ряд). Если каждый член ряда нормален не во всей группе, а только в предыдущем члене, то такой ряд наз. субнормальным. Кроме конечных рассматриваются также бесконечные убывающие и бесконечные… … Математическая энциклопедия

Нормальный ряд подгрупп — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия

Центральный ряд подгрупп — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия

Центральный ряд — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия

ПОДГРУПП РЯД — конечная цепочка вложенных одна в другую подгрупп группы G: (*) или Рассматриваются также бесконечные цепочки вложенных подгрупп (убывающие и возрастающие), занумерованные порядковыми числами или даже элементами упорядоченного множества. Их чаще… … Математическая энциклопедия

ЦЕНТРАЛЬНЫЙ РЯД — группы нормальный ряд, все факторы к рого центральны, т. е. ряд подгрупп для к рого Gi+1/G лежит в центре группы G/Gi для всех i (см. также Подгрупп ряд). Если для всех i подгруппа Gi+1/Gi в точности совпадает с центром группы G/Gi то ряд наз.… … Математическая энциклопедия

Список магматических горных пород — Интрузивные горные породы Гипабисальные горные породы Эффузивные горные породы Ультраосновные горные породы Нормальный ряд оливинит, дунит, и семейство перидотитов, где выделяются гарцбургиты, лерцолиты, верлиты и роговообманковые перидотиты… … Википедия

Глоссарий теории групп — Группа (математика) Теория групп … Википедия

Словарь терминов теории групп — Для общего ознакомления с теорией групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И К Л М Н О П Р … Википедия

Источник

Расширение группы

Для общего описания теории групп см. Группа (математика) и Теория групп.

Курсив обозначает ссылку на этот словарь.

p-группа — группа, все элементы в которой имеют порядок, равный некоторой степени простого числа p (не обязательно одинаковой у всех элементов). Также говорят о примарной группе. Более подробно см. в статье конечная p-группа.

Аддитивная группа кольца ― группа, элементами которой являются все элементы данного кольца, а операция совпадает с операцией сложения в кольце.

Антигомоморфизм групп — отображение групп f : (G,*) → (H,×) такое, что

для произвольных a и b в G (сравните с гомоморфизмом).

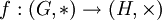
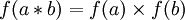
Гомоморфизм групп — отображение групп такое, что

для произвольных a и b в G.

Группа Шмидта — это ненильпотентная группа, все собственные подгруппы которой нильпотентны.

Группа Миллера — Морено — это неабелева группа, все собственные подгруппы которой абелевы.

Групповая алгебра группы G над полем K — это векторное пространство над K, образующими которого являются элементы G, а умножение образующих соответсвует умножению элементов G.

Длина ряда подгрупп — число n в определении ряда подгрупп.

Изоморфизм групп — биективный гомоморфизм.

Изоморфные группы — группы, между которыми существует хотя бы один изоморфизм.

Индекс подгруппы H в группе G — число смежных классов в каждом (правом или левом) из разложений группы G по этой подгруппе H.

Индексы ряда подгрупп — индексы | G_{i + 1}:G_i | в определении субнормального ряда подгрупп.

Класс смежности/смежный класс (левый или правый) подгруппы H в G. Левый класс смежности элемента 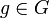по подгруппе H в G есть множество

Аналогично определяется правый класс смежности:

Класс сопряжённости элемента 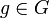есть множество

Коммутант группы есть подгруппа, порождённая всеми коммутаторами группы, обычно обозначается [G,G] или .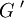

Коммутативная группа. Группа G является коммутативной, или абелевой, если её операция * коммутативна, то есть g*h=h*g .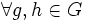

Коммутатор подгрупп — множество всевозможных произведений .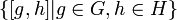

Композиционный ряд группы G — ряд подгрупп, в котором все факторы G_{i + 1} / G_i — простые группы.

Конечная группа — группа с конечным числом элементов.

Конечно определённая группа — группа, обладающая конечным числом образующих и задаваемая в этих образующих конечным числом соотношений.

Конечнопорождённая группа — группа, обладающая конечной системой образующих.

Кручение, TorG, коммутативной или нильпотентной группы G есть подгруппа всех элементов конечного порядка.

Локальная теорема. Говорят, что для некоторого свойства P групп справедлива локальная теорема, если всякая группа, локально обладающая этим свойством, сама обладает им.

Например: локально абелева группа является абелевой, но локально конечная группа может быть бесконечной.

Метабелева группа ― группа, второй коммутант которой тривиален (разрешимая ступени 2).

Метациклическая группа ― группа, обладающая циклической нормальной подгруппой, факторгруппа по которой также циклическая. Всякая конечная группа, порядок которой свободен от квадратов (то есть не делится на квадрат какого-либо числа), является метациклической.

Мультипликативная группа тела ― группа, элементами которой являются все ненулевые элементы данного тела, а операция совпадает с операцией умножения в теле.

Нильпотентная группа — группа, обладающая центральным рядом подгрупп. Минимальная из длин таких рядов называется её классом нильпотентности.

Норма группы — совокупность элементов группы, перестановочных со всеми подгруппами, то есть пересечение нормализаторов всех её подгрупп.

Нормализатор подгруппы H в G — это максимальная подгруппа G, в которой H нормальна. Иначе говоря, нормализатор есть стабилизатор H при действии G на множестве своих подгрупп сопряжениями, то есть

Нормальная подгруппа (инвариантная подгруппа, нормальный делитель). H есть нормальная подгруппа G, если для любого элемента g в G gH = Hg, то есть правые и левые классы смежности H в G совпадают. Иначе говоря, если .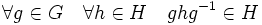

Период группы ― наименьшее общее кратное порядков элементов данной группы.

Периодическая группа ― группа, каждый элемент которой имеет конечный порядок.

Подгруппа — подмножество H группы G, которое является группой относительно операции, определённой в G.

Подгруппа кручения см. кручение.

Для произвольного подмножества S в G, обозначает наименьшую подгруппу G, содержащую S.

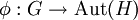
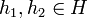
Полупрямое произведение групп G и H над гомоморфизмом (обозначается по разному, в том числе G ⋊_φ H) — множество G × H, наделенное операцией *, для которой (g₁,h₁) * (g₂,h₂) = (g₁φ(h₁)(g₂),h₁h₂) для любых , .

Порядок группы (G,*) — мощность G (то есть число её элементов).

Порядок элемента g группы G — минимальное натуральное число m такое, что g m = e. В случае, если такого m не существует, считается, что g имеет бесконечный порядок.

Простая группа — группа, в которой нет нормальных подгрупп, кроме тривиальной <e> и всей группы.

Примарная группа — группа, все элементы в которой имеют порядок, равный некоторой степени простого числа p (не обязательно одинаковой у всех элементов). Также говорят о p-группе.

Расширение группы — группа, содержащая данную группу в качестве нормальной подгруппы.

Разрешимая группа — группа, обладающая нормальным рядом подгрупп с абелевыми факторами. Наименьшая из длин таких рядов называется её ступенью разрешимости.

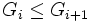
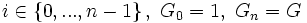
Ряд подгрупп — конечная последовательность подгрупп G₀,G₁. G_n называется рядом подгрупп, если , для всех . Такой ряд записывают в виде

Сверхразрешимая группа — группа, обладающая нормальным рядом подгрупп с циклическими факторами.

Свободная группа, порождённая множеством A — это группа, порождённая элементами этого множества и не имеющая никаких соотношений, кроме соотношений, определяющих группу. Все свободные группы, порождённые равномощными множествами, изоморфны.

Соотношение — тождество, которому удовлетворяют образующие группы (при задании группы образующими и соотношениями).

Факторгруппа группы G по нормальной подгруппе H есть множество классов смежности подгруппы H с умножением, определяемым следующим образом:

Факторы субнормального ряда — фактор-группы G_{i + 1} / G_i в определении субнормального ряда подгрупп.

Холлова подгруппа — подгруппа, порядок которой взаимно прост с её индексом во всей группе.

Центр группы G, обычно обозначается Z(G), определяется как

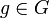
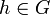
Z(G) = <| gh = hg для любого >,

иначе говоря, это максимальная подгруппа элементов, коммутирующих с каждым элементом G.

Централизатор элемента есть максимальная подгруппа, коммутирующая с этим элементом.

Центральный ряд подгрупп — нормальный ряд подгрупп, в котором 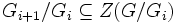, для всех членов ряда.

Циклическая группа — группа, состоящая из порождающего элемента и всех его целых степеней. Конечна в случае, если порядок порождающего элемента конечен.

Ядро гомоморфизма — прообраз нейтрального элемента при гомоморфизме. Ядро всегда есть нормальная подгруппа, более того, любая нормальная подгруппа есть ядро некоторого гомоморфизма.

Литература

Полезное

Смотреть что такое «Расширение группы» в других словарях:

расширение (в телекоммуникационных технологиях) — расширение Процесс добавления в исходный сигнал группы кодированных символов, которые в дальнейшем обрабатываются и преобразуются как единый сигнал. [Л.М. Невдяев. Телекоммуникационные технологии. Англо русский толковый словарь справочник. Под… … Справочник технического переводчика

РАСШИРЕНИЕ — д и ф ф е р е н ц и а л ь н о г о п о л я F0 дифференциальное поле FЙF0. с таким множеством дифференцирований D, что ограничение D на F0 совпадает с множеством дифференцирований, заданных на F0. В свою очередь F0 будет д и ф ф ер е н ц и а л ь н… … Математическая энциклопедия

РАСШИРЕНИЕ — п о л у г р у п п ы А полугруппа S, содержащая Ав качестве подполугруппы. Обычно речь идет о расширениях полугруппы А, связанных с Атеми или иными условиями. Наиболее развита теория идеальных Р. полугрупп (полугрупп, содержащих Ав качестве… … Математическая энциклопедия

Расширение территории Москвы (2011—2012) — Данные в этой статье приведены по состоянию на 26 июня 2012. Вы можете помочь … Википедия

РАСШИРЕНИЕ — г р у п п ы группа, содержащая данную группу в качестве нормального делителя. Обычно фиксируется и факторгруппа, т. е. р а с ш и р е н и е м г р у п п ы Ап р и п о м о щ и г р у пп ы Вназ. группа G, содержащая Ав качество нормального делителя и… … Математическая энциклопедия

Группы самопомощи (self-help groups) — Г. с. представляют собой более или менее формальные орг ции непрофессионалов, преследующих общую цель ради достижения блага для каждого члена группы. Речь идет о группах, главная цель к рых изменения в психологии или поведении участников. Они… … Психологическая энциклопедия

Группы самопомощи — (self help groups) более или менее формальные группы непрофессионалов, преследующих общую цель (изменение психологии или поведения участников) ради достижения блага для каждого члена группы. Группа, состоит из лиц, объединенных общими… … Психология общения. Энциклопедический словарь

Изоморфные группы — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия

Источник