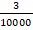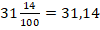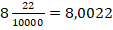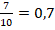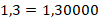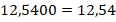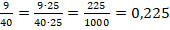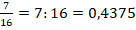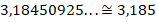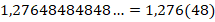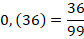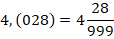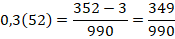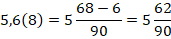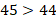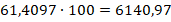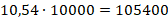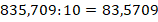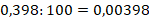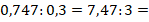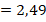Что такое нулевая дробная часть

Десятичная дробь

Десятичные дроби: определение, сложение, вычитание, умножение, деление, сравнение

Десятичная дробь является частным случаем обыкновенных дробей (у которой знаменатель кратен 10).

Определение

Десятичными называют дроби, знаменатели которых представляют собой числа, состоящие из единицы и некоторого количества следующих за нею нулей. То есть это дроби со знаменателем 10, 100, 1000 и т.д. Иначе десятичную дробь можно охарактеризовать как дробь со знаменателем 10 или одной из степеней десятки.

, ,

Десятичная дробь записывается иначе, чем обыкновенная. Операции с этими дробями также отличны от операций с обыкновенными. Правила действий над ними в значительной мере приближены к правилами действий над целыми числами. Этим, в частности, обусловлена их востребованность при решении практических задач.

Представление дроби в десятичной записи

В записи десятичной дроби нет знаменателя, в ней отображено число числителя. В общем виде запись десятичной дроби осуществляется по такой схеме:

где Х – целая часть дроби, Y – ее дробная часть, «,» – десятичная запятая.

Для правильного представления обыкновенной дроби в виде десятичной требуется, чтобы она была правильной, то есть с выделенной целой частью (если это возможно) и числителем, который меньше знаменателя. Тогда в десятичной записи целая часть записывается до десятичной запятой (Х), а числитель обыкновенной дроби – после десятичной запятой (Y).

Если в числителе представлено число с количеством знаков, меньшим, чем количество нулей в знаменателе, то в части Y недостающее количество знаков в десятичной записи заполняется нулями впереди цифр числителя.

Пример:

Если обыкновенная дробь меньше 1, т.е. не имеет целой части, то для Х в десятичном виде записывают 0.

В дробной части (Y), после последнего значимого (отличного от нуля) разряда, может быть вписано произвольное количество нулей. На значение дроби это не влияет. И наоборот: все нули в конце дробной части десятичной дроби можно опустить.

Прочтение десятичных дробей

Часть Х читается в общем случае так: «Х целых».

Часть Y прочитывается в соответствии с числом в знаменателе. Для знаменателя 10 следует читать: «Y десятых», для знаменателя 100: «Y сотых», для знаменателя 1000: «Y тысячных» и так далее… 😉

Более корректным считается другой подход к прочтению, основанный на подсчете количества разрядов дробной части. Для этого нужно понимать, что дробные разряды расположены в зеркальном отражении по отношению к разрядам целой части дроби.

Наименования для правильного прочтения приведены в таблице:

Исходя из этого, прочтение должно опираться на соответствие наименованию разряда последней цифры дробной части.

Перевод произвольной обыкновенной дроби в десятичную

Если в знаменателе обыкновенной дроби стоит 10 или какая-нибудь степень десятки, то перевод дроби выполняется как описано выше. В остальных ситуациях необходимы дополнительные преобразования.

Существует 2 способа перевода.

Первый способ перевода

Числитель и знаменатель необходимо домножить на такое целое число, чтобы в знаменателе было получено число 10 или одна из степеней десятки. А далее дробь представляется в десятичной записи.

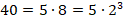
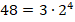
Этот способ применим для дробей, знаменатель которых раскладывается только на 2 и 5. Так, в предыдущем примере . Если же в разложении присутствуют другие простые множители (например, ), то придется прибегнуть ко 2-му способу.

Второй способ перевода

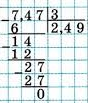
2-й способ заключается в делении числителя на знаменатель в

Правило деления в столбик, приводящее в результате к десятичной дроби, описано ниже (см. Деление десятичных дробей).

Перевод десятичной дроби в обыкновенную

Для этого следует ее дробную часть (справа от запятой) записать в виде числителя, а результат прочтения дробной части – в виде соответствующего числа в знаменателе. Далее, если это возможно, нужно сократить полученную дробь.

Конечная и бесконечная десятичная дробь

Конечной называют десятичная дробь, дробная часть которой состоит из конечного количества цифр.

Выше все приведенные примеры содержат именно конечные десятичные дроби. Однако не всякую обыкновенную дробь возможно представить в виде конечной десятичной. Если 1-й способ перевода для данной дроби не применим, а 2-й способ демонстрирует, что деление невозможно завершить, значит, получена может быть только бесконечная десятичная дробь.

В полном виде бесконечную дробь записать невозможно. В неполном же виде такие дроби можно представить:

Периодической называется дробь, у которой после запятой можно выделить повторяющуюся бесконечно последовательность цифр.

Остальные дроби называются непериодическими. Для непериодических дробей допустим только 1-й способ представления (округление).

Пример периодической дроби: 0,8888888… Здесь налицо повторяющаяся цифра 8, которая, очевидно, будет повторяться до бесконечности, поскольку нет оснований предполагать иное. Эта цифра называется периодом дроби.

Периодические дроби бывают чистыми и смешанными. Чистой является десятичная дробь, у которой период начинается непосредственно после запятой. У смешанной дроби до периода после запятой имеется 1 или больше цифр.

54,33333… – периодическая чистая десят.дробь

2,5621212121… – периодическая смешанная дробь

Примеры записи бесконечных десятичных дробей:

Во 2-м примере показано, как правильно оформлять период в записи периодической дроби.

Перевод периодических десятичных дробей в обыкновенные

Для перевода чистой периодической дроби в обыкновенную ее период записывают в числитель, а в знаменатель пишут число, состоящее из девяток в количестве, равном количеству цифр в периоде.

Смешанная периодическая десятичная дробь переводится следующим образом:

Сравнение десятичных дробей

Десятичные дроби сравнивают первоначально по их целым частям. Больше та дробь, у которой больше ее целая часть.

Если целые части одинаковы, то сравнивают цифры соответствующих разрядов дробной части, начиная с первого (с десятых). Здесь действует тот же принцип: больше та из дробей, у которой больше разряд десятых; при равенстве цифр разряда десятых сравнивают разряды сотых и так далее.

, поскольку

, поскольку при равных целых частях и равных десятых в дробной части у 2-й дроби больше цифра сотых.

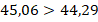
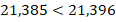
Сложение и вычитание десятичных дробей

Десятичные дроби складывают и вычитают так же, как и целые числа, записав соответствующие цифры друг под другом. Для этого нужно, чтобы друг под другом находились десятичные запятые. Тогда единицы (десятки и т.д.) целой части, а также десятые (сотые и т.д.) дробной окажутся в соответствии. Недостающие разряды дробной части заполняют нулями. Непосредственно процесс сложения и вычитания осуществляется так же, как и для целых чисел.

Примеры:

Умножение десятичных дробей

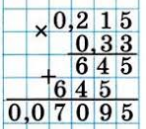
Для умножения десятичных дробей нужно записать их друг под другом, выровняв по последней цифре и не обращая внимания на местоположение десятичных запятых. Затем нужно перемножить числа так же, как и при умножении целых чисел. После получения результата следует пересчитать количество цифр после запятой в обоих дробях и отделить запятой в результирующем числе суммарное количество дробных разрядов. Если разрядов не хватает, то они заменяются нулями.

Умножение и деление десятичных дробей на 10 n

Примеры:

Деление десятичной дроби и целого числа на целое число и на десятичную дробь

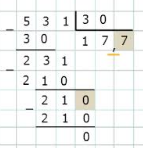
Деление в столбик десятичной дроби на целое число выполняется аналогично делению двух целых чисел. Дополнительно требуется только учет положения десятичной запятой: при сносе цифры разряда, за которым следует запятая, необходимо поставить запятую после текущей цифры формируемого ответа. Далее нужно продолжать делить до получения нуля. Если знаков в делимом для полного деления недостает, в их качестве следует использовать нули.

Аналогично делятся в столбик 2 целых числа, если снесены все цифры делимого, а полное деление еще не завершено. В этом случае после сноса последней цифры делимого ставится десят.запятая в формирующемся ответе, а в качестве сносимых цифр используют нули. Т.е. делимое здесь, по сути, представляют как десятичную дробь с нулевой дробной частью.

Пример:

Графическое представление десятичных дробей

Графически десятичные дроби изображаются посредством координатной прямой. Для этого единичные отрезки делят дополнительно на 10 равных долей подобно тому, как на линейке откладываются одновременно сантиметры и миллиметры. Это обеспечивает точное отображение десятичных дробей и возможность объективного их сравнения.

Чтобы дольные деления на единичных отрезках были одинаковыми, следует тщательно продумывать длину самого единичного отрезка. Она должна быть такой, чтобы можно было обеспечить удобство дополнительного деления.

Источник

Целая и дробная части числа

Разделы: Математика

Цели урока: познакомить учащихся с понятием целой и дробной части числа; сформулировать и доказать некоторые свойства целой части числа; познакомить учащихся с широким спектром применения целой и дробной части числа; совершенствовать умение решать уравнения и системы уравнений, содержащих целую и дробную части числа.

Оборудование: плакат “Кто смолоду делает и думает сам, тот и становится потом надёжнее, крепче, умнее” (В. Шукшин).
Проектор, магнитная доска, справочник по алгебре.

I. Организационный момент: сообщение темы урока; постановка цели урока; сообщение этапов урока.

II. Проверка домашнего задания.

Ответить на вопросы учащихся по домашнему заданию. Решить задачи, вызвавшие затруднения при выполнении домашней работы.

III. Изучение нового материала.

Во многих задачах алгебры приходится рассматривать наибольшее целое число, не превосходящее данного числа. Такое целое число получило специальное название “целая часть числа”.

Целой частью действительного числа х называется наибольшее целое число, не превосходящее х. Целая часть числа х обозначается символом [x] или Е(х) (от французского Entier “антье” ─ “целый”). Например, [5] = 5, [ π ] = 3,

Из определения следует, что [x] ≤ х, так как целая часть не превосходит х.

С другой стороны, т.к. [x] – наибольшее целое число, удовлетворяющее неравенству, то [x] +1>х. Таким образом, [x] есть целое число, определяющееся неравенствами [x] ≤ х α = υ ─ [x] называют дробной частью числа х и обозначают <х>. Тогда имеем: 0 ≤ <х>0 ≤ α о [x+у] = [x] + [у].

Это свойство распространяется на любое конечное число слагаемых:

Умение находить целую часть величины очень важно в приближенных вычислениях. В самом деле, если мы умеем находить целую часть величины х, то, приняв [x] или [x]+1 за приближенное значение величины х, мы сделаем погрешность, величина которой не больше единицы, так как

Поскольку х – целое число, то остается проверить значения от 0 до 6. Решениями уравнения оказываются числа 0,4 и 5.

Задача 7. Решить систему уравнение

(Провести проверку с помощью проектора.)

Найти число корней уравнения

Преобразуем, неравенство к виду , откуда получим, что искомое количество целых чисел равно 5. Значит, число корней данного уравнения равно 5.

Задача 9. (Соросовская олимпиада).

а) провести проверку самостоятельных работ с помощью проектора;

б) ответить на вопросы:

в) выставление отметок.

VI. Домашнее задание.

Дополнительная задача (по желанию).

Некто измерил длину и ширину прямоугольника. Он умножил целую часть длины на целую часть ширины и получил 48; умножил целую часть длины на дробную часть ширины и получил 3,2; умножил дробную часть длины на целую часть ширины и получил 1,5. Определите площадь прямоугольника.

Источник

Урок №4 Дробные числа и цикл if

Теория

Практика

Домашнее задание

Дробные числа

Операция деления с остатком

Цикл if

I Дробные числа

В прошлом уроке мы прошли целые числа: как они хранятся, считываются, выписываются и обрабатываются в языке программирования С/С++. Но в математике целые числа занимают лишь малую часть среди всех чисел. Потому что есть ещё и дробные числа, и они, конечно же, тоже есть и в языке программирования С/С++.

Хранение дробных чисел

Дробные числа хранятся в переменных типа double (от англ. double — двойной). Данный тип так называется, потому что для хранения дробного числа необходимо использовать две ячейки в памяти: для целой и для дробной части.

Целая часть числа

Дробная часть числа

Для того, чтобы вычислить дробную часть числа в языке программирования С/С++, необходимо вычесть из этого числа его целую часть.

Но бывают дробные числа, дробная часть которых бесконечна. Такие числа хранятся в компьютере с некоторой точностью в силу невозможности хранить бесконечное число чисел.

Создание переменной типа double

Чтобы создать переменную типа double :

Как и в случае с целыми переменными, рекомендуется сразу же очищать переменную от мусора, присваиванием ей нулевое значение:

Считывание дробных чисел с клавиатуры

Считывание дробных чисел с клавиатуры в языке программирования С/С++ происходит аналогично считыванию целых чисел с помощью функции scanf() за исключением другого типа данных (6 строка):

Вывод дробных чисел на экран

Вывод дробных чисел на экран в языке программирования С/С++ происходит аналогично выводу целых чисел с помощью функции printf() (7-8 строки):

Формат вывода дробных чисел на экран

В языке программирования С/С++ можно регулировать, сколько цифр после точки будет выписано на экран. По умолчанию выписываются 6 цифр после точки.

Чтобы указать, сколько цифр после точки необходимо отобразить, можно написать следующий код (7-8 строки):

Пример вывода данного кода:

II Операция деления с остатком

В языке программирования С/С++ есть операция деления с остатком. Более того, данная операция является очень популярной и широко используемой.

Определение оператора %

Для того, чтобы узнать остаток при делении одного числа на другое, существует специальный оператор, обозначающийся символом процента % :

Остаток при делении отрицательных чисел

Процедура универсализации взятия остатка написана в данном уроке чуть ниже.

III Цикл if

Мы начинаем знакомство с таким объектом языка программирования С/С++, как цикл. В языке программирования С/С++ есть несколько основных базовых циклов.

Определение

Разновидности условий

В качестве условий могут выступать совершенно любые математические выражения, которые могут быть абсолютно точно истинными или же абсолютно точки ложными. Например, условие «Среди чисел от 1 до 1000 есть число, которое делится на все положительные однозначные числа» указать в цикле if нельзя.

Условие должно быть односложным и легкопроверяемым компьютером с точки зрения вычисления. Условия могут быть как на созданные ранее переменные, так и на конкретные числа. Рассмотрим самые популярные разновидности условий:

Выражения со знаками:

В программировании существуют точно такие же знаки, что и в математике:

Условие пишется в круглых скобочках через пробел после названия цикла:

Выражения, требующие вычисления:

Для этого, конечно можно создать дополнительную переменную, положить в неё сумму, а потом уже сравнить эту сумму и число c в цикле if :

Однако это не очень удобно с точки зрения лишнего кода, а также использования памяти, необходимо для создания новой переменной.

Данное сравнение можно осуществить гораздо удобней, сразу сравнив результат суммы и число:

Внутри цикла if можно вычислять выражения любой сложности:

Проверка делимости одного числа на другое:

Поэтому проверить делимость числа a на число b в программе можно следующим образом:

Сложные условия в цикле if:

Иногда необходимо проверить сразу несколько условий. Например, что число чётное и положительное. В таком случае можно воспользоваться двумя циклами if :

Но иногда условия могут быть сложней: проверить, что число чётное, положительное и не делится на 7. И создавать для этого три вложенных друг в друга цикла if достаточно долго. Вместо этого можно воспользоваться одним циклом if со сложным условием, состоящем из нескольких простых:

Чтобы в одном цикле if проверить, что число кратно 11 или 13, необходимо воспользоваться связкой «ИЛИ»:

Иерархия простых условий в составе сложного:

Важно понимать, что связка «ИЛИ» относится к связке «И» точно также, как операция сложения к операции умножения.

Допустим, необходимо проверить условие, что число положительное, чётное и при этом кратно или 11 или 13.

Можно написать просто:

И это будет неправильно. Перейдём от условий к выражениям с операциями сложения и умножения:

(a>0) \times (a \% 2 == 0) \times (a \% 11 == 0) + (a \% 13 == 0)

Совершенно логично, что сначала будет произведено умножение, а только потом сложение полученного произведения с последним слагаемым. Но ведь нам необходимо, чтобы число гарантированно было чётно и положительно, и только потом кратно 11 или 13.

В стандартной арифметике для этого используются скобки:

(a>0) \times (a \% 2 == 0) \times \Big( (a \% 11 == 0) + (a \% 13 == 0)\Big)

В языке программирования происходит тоже самое. Чтобы условие работало корректно, необходимо добавить скобки:

Конструкция else

Допустим, необходимо разделить число на 2 и выписать его на экран, если оно чётное, и просто выписать его на экран, если нечётное. Для этого и нужно использовать else :

Всё просто: «Если число a чётно, делим его на 2 и выписываем, иначе просто выписываем его».

Конструкция else if

Данная конструкция может быть использована и в ещё более сложном условии. Например, необходимо сделать что-то конкретное, в зависимости от остатка при делении на 3. Так как при делении на 3 может быть три остатка (0, 1 и 2), обыкновенно конструкцией «если. иначе. » ограничиться нельзя. В таком случае можно воспользоваться:

Взятие остатка от отрицательного числа

Как уже было замечено, в языке программирования С/С++ операция взятия остатка от отрицательных чисел работает не так, как принято у математиков. Если есть вероятность, что программному коду нужно будет работать с отрицательными числами, необходимо не просто брать остаток при делении одного числа на другое, а осуществлять проверку, с положительным или отрицательным числом идёт работа:

Однако можно поступить проще. Так как ясно, что в языке программирования С/С++ при делении с остатком отрицательных чисел получается остаток, равный разности принятого у математиков остатка и делителя.

Таким образом, например, при нахождении чисел, имеющих остаток 4 при делении на 11, можно написать следующее условие в цикле if :

Источник

Методическое пособие на тему «Целая и дробная часть числа»

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

История и определение целой и дробной части числа

Оккама считают одним из предшественников великих мыслителей Рене Декарта и Иммануила Канта. Согласно его философским воззрениям, реальность есть бытие конкретной вещи, поэтому «тщетно делать с большим то, что можно делать с меньшим». Это высказывание стало основой принципа экономии мышления. Уильям Оккам применял его с такой разящей силой, что он получил впоследствии столь популярное сейчас название «бритвы Оккама».

Для многих людей, не сведущих в математике, общим местом стали вопросы типа «Что же ещё можно открыть в математике?». Учитывая математическую подготовленность спрашивающих, можно предположить, что речь идёт только о математике школьного уровня. Вполне в духе Оккама мы предлагаем вопрошающим, и в первую очередь самим учащимся, некоторые задачи, варьирующие хорошо знакомые им понятия целой и дробной частей числа. На этих задачах мы покажем, как важно рассматривать не каждую задачу в отдельности, а соединять их в систему, разрабатывая общий алгоритм решения. Такой методический приём диктует нам принцип экономии мышления Оккама.

Определение: целой частью числа х называется наибольшее целое число с, не превышающее х, т.е. если [х] = с, c ≤ x c + 1.

Обозначается целая часть действительного числа x символом [x] или E(x).

Простейшие свойства функции y = [x]:

1. Область определения функции y = [x] есть множество всех действительных чисел R.

3. Функция y = [x] кусочно-постоянная.

4. Функция y = [x] неубывающая, т. е. для любых х ₁ и х ₂ из R таких,

5. Для любого целого числа n и любого действительного числа x выполняется равенство: [x + n] = [x] + n.

7. Для любого действительного числа х верно соотношение

[x] ≤ x ─ целое число, т. е. х Z.

Возникает вопрос: «Если есть функция целой части числа, может, есть и функция дробной части числа?»

Построим график функции у = <х>. Он выглядит следующим образом:

Простейшие свойства функции y = :

1. Область определения функции y = есть множество всех действительных чисел R.

2. Область значений функции y = есть полуинтервал [0;1).

3. Функция y = ограничена, т. е. для любого действительного числа x имеет место соотношение: 0 ≤

4. Для любого целого числа n и любого действительного числа х выполняется равенство: = , т. е. функция y = — периодическая с основным периодом, равным единице.

Представление о том, как выглядят графики функций у = [х] и у = <х>поможет выполнить и некоторые задания.

1) Построить графики функций:

2) Какими могут быть числа х и у, если:

4) Что больше: [а] или <а>?

2.1. Простейшие уравнения

К простейшим уравнениям относятся уравнения вида [х] = а.

Уравнения такого вида решаются по определению:

Рассмотрим пример решения одного из таких уравнений:

Это и будет являться решением уравнения.

Ответ: х[-6,3;-5,3).

Рассмотрим ещё одно уравнение, относящееся к разряду простейших:

Доказательство: х = [х] +

х = k + а, где k = [х], а =

Ответ: х[6;7).

Рассмотрим более сложное уравнение:

Получаем х(1;4)

РЕШИТЕ ПРЕДЛОЖЕННЫЕ УРАВНЕНИЯ САМОСТОЯТЕЛЬНО:

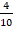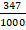Источник