Что такое нулевой отрезок

нулевой отрезок

Смотреть что такое «нулевой отрезок» в других словарях:

Нулевой год — Это статья об ошибочной нумерации лет в календаре, см. также статью о числе 0. Нулевой год не существует согласно григорианскому или юлианскому летоисчислению. Его упоминание связано с расчётом лет согласно номерам целых чисел на координатной… … Википедия

Направленный отрезок — Под направленным отрезком в геометрии понимают упорядоченную пару точек, первая из которых точка A называется его началом, а вторая B его концом. Содержание 1 Определение … Википедия

Транслёр — Отрезок транслорного рельса. Транслёр (или Транслор; англ. Translohr) трамвай на шинах, использующий усовершенствованное крепление к единственному рельсу. Разработан и производится … Википедия

ДЕЛЕНИЕ ШКАЛЫ — отрезок шкалы между двумя соседними градуировочными отметками на аналоговой шкале. Д. ш. используется как единица счета для выражения показаний. При этом принимается во внимание, что индикаторная метка (указатель) начиная от нулевой отметки… … Энциклопедический словарь по психологии и педагогике

Вектор (математика) — Вектор У этого термина существуют и другие значения, см. Вектор … Википедия

ЭРГОДИЧЕСКАЯ ТЕОРИЯ — Введение Э. т. (метрическая теория динамических систем) раздел теории динамических систем, изучающий их статистич. свойства. Возникновение Э. т. (1 я треть 20 в.) было стимулировано попытками доказать эргодическую гипотезу (термин введён П. и Т.… … Физическая энциклопедия

ГОСТ Р 50779.10-2000: Статистические методы. Вероятность и основы статистики. Термины и определения — Терминология ГОСТ Р 50779.10 2000: Статистические методы. Вероятность и основы статистики. Термины и определения оригинал документа: 2.3. (генеральная) совокупность Множество всех рассматриваемых единиц. Примечание Для случайной величины… … Словарь-справочник терминов нормативно-технической документации

ВЕКТОР — В физике и математике вектор это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент,… … Энциклопедия Кольера

ГОСТ Р 50030.5.1-2005: Аппаратура распределения и управления низковольтная. Часть 5. Аппараты и коммутационные элементы цепей управления. Глава 1. Электромеханические аппараты для цепей управления — Терминология ГОСТ Р 50030.5.1 2005: Аппаратура распределения и управления низковольтная. Часть 5. Аппараты и коммутационные элементы цепей управления. Глава 1. Электромеханические аппараты для цепей управления оригинал документа: (обязательное)… … Словарь-справочник терминов нормативно-технической документации

В Америке есть таланты (сезон 3) — Производство NBC Ведущий(е) Джерри Спрингер Страна производства США Судьи Дэвид Хасселхофф Пирс Морган Шэрон Осборн Количество выпусков В Америке есть таланты … Википедия

МАГНИТЫ И МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА — Простейшие проявления магнетизма известны очень давно и знакомы большинству из нас. Однако объяснить эти, казалось бы, простые явления на основе фундаментальных принципов физики удалось лишь сравнительно недавно. Существуют магниты двух разных… … Энциклопедия Кольера

Источник

Отрезок — что это такое

Что такое отрезок? Ответ на этот вопрос кажется весьма простым, когда вы учитесь в школе. Но с возрастом школьный курс математики постепенно забывается настолько, что такие простые вещи становятся не столь очевидными.

Отрезок — что это за фигура

Не стоит недооценивать значимость геометрических понятий в человеческой жизни, так как иногда эти знания помогают решать вполне реальные задачи, а не только блистать кругозором в кругу друзей.

Отрезок — это составная часть прямой, расположенная между двумя точками.

Вы можете дать определение также исходя из структурного подхода:

Отрезок — это такая математическая фигура, которая состоит из следующих элементов:

С этими составными частями вы можете ознакомиться на слайде:

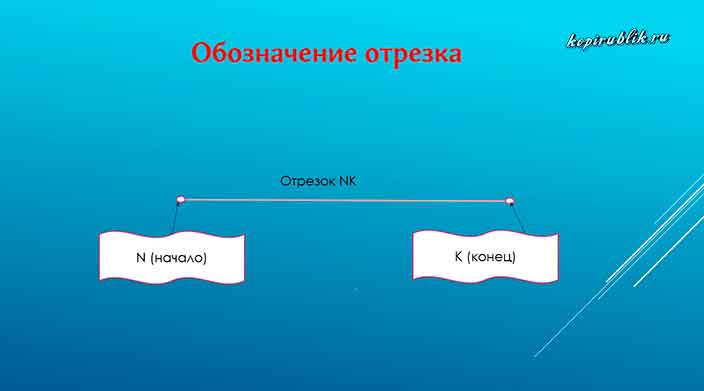
В связи с тем, что границы отрезка отмечаются точками, которые в рамках математики выделяются латинскими буквами, сама фигура описывается двумя буквами, например, NK.

Пример визуального изображения отрезка вы видите на рисунке: точки N и K являются началом и концом.

Важная характеристика, которая присуща любому отрезку – его длина.

Основные меры измерения длины отрезков– это миллиметр, сантиметр, метр, километр.

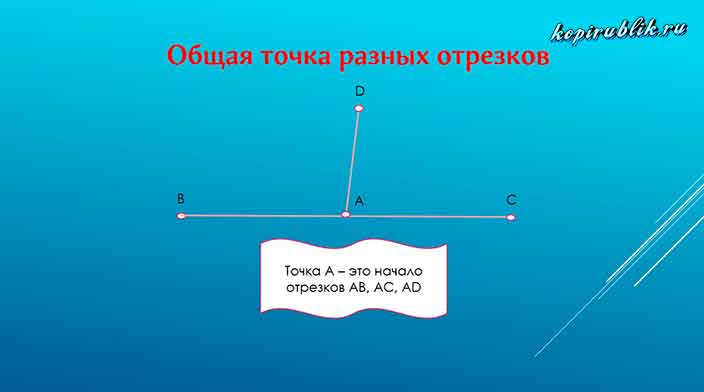
Из математической трактовки следует, что отрезок – это такая прямая, которая расположена между двумя точками не выходя за их пределы. При этом одна же точка может быть концом множества отрезков.

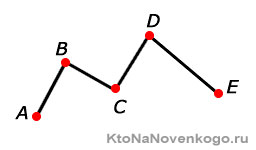
Такую ситуацию вы видите на рисунке: точка А является общей для всех отрезков. При этом точки B, C, D — индивидуальны для каждого из отрезков.

Сравнение отрезка с геометрическими фигурами

В математике существуют три очень похожих понятия – это отрезок, луч, прямая. Учащиеся нередко задают такой вопрос «Что такое отрезок, чем он отличается от луча и прямой?». Давайте сразу определимся с понятиями, которые позволят вам понять разницу между фигурами.

Отрезок — это часть линии, которая проходит от точки начала до точки, обозначающей конец.

Луч — составная часть прямой, которая ограничена точкой с одной стороны. С другого конца луч продлевается до бесконечности.

Прямая — это линия, не подверженная искривлениям, у которой к тому же, в отличие от отрезков, отсутствуют начало и конец.

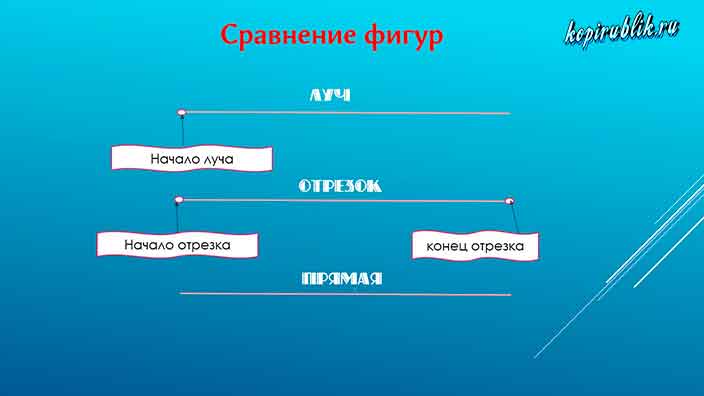
Сравнив 3 понятия, вы можете убедиться, что луч совмещает ограниченность отрезка и бесконечность прямой.

Примечательно, что прямая и луч бесконечны, поэтому вы сможете измерить длину только у отрезков.

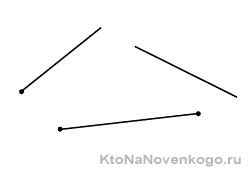
У вас может возникнуть вопрос: «Как быстро определить, что именно перед вами — отрезок, луч или прямая?». Визуально идентифицировать геометрические фигуры можно по количеству ограничивающих их длину точек:

Направленный отрезок

В статье вы увидели базовый вид отрезка — ненаправленный. Это отрезок, у которого невозможно определить, что является его началом, а что — концом.

Существует второй вид отрезков – направленные.

Альтернативное название этой математической фигуры — вектор.

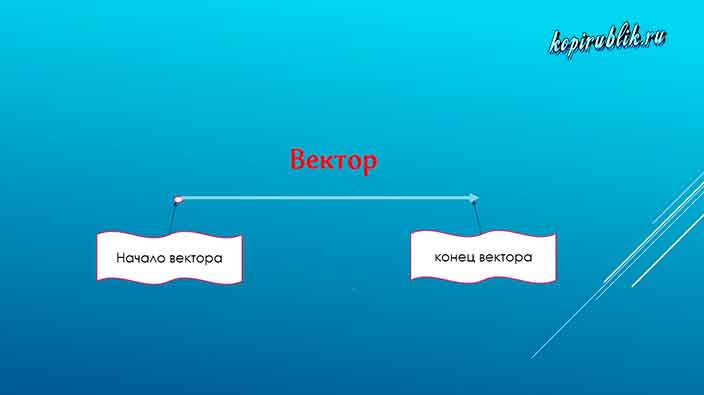
Особенностью направленного отрезка является то, что одна из точек, ограничивающих его длину, обозначается стрелкой. Она указывает, что именно там находится конец. Соответственно часть вектора, обозначенная точкой — это его начало.

Характерной чертой вектора является то, что он может быть описан не только двумя латинскими буквами, но и одной маленькой буквой, над которой располагается стрелка.

Направленный отрезок вместо показателя длины имеет характеристику — модуль, которая измеряется величинами, измеряющими расстояние – миллиметр, сантиметр, метр, километр.

В процессе работы с отрезками возникает вопрос: «Как рассчитать модуль вектора с использованием системы координат?».

Вы определите его следующим образом:

Направленные отрезки, которые лежат на одной прямой или параллельных прямых – это коллинеарные направленные отрезки.

Направленные отрезки, расположенные на параллельных прямых – это коллинеарные направленные отрезки.

Нулевой вектор — это отрезок, у которого одна точка включает начало и его конец.

Отрезки, соединённые в ломаную линию

Ломаная линия — это совокупность соединённых между собой отрезков, в которой окончание одного отрезка совпадает с начальной точкой другого. Каждая из составных частей ломаной линии называется звеном.

Ломаная линия содержит три типа вершин — точек, из которых состоят отрезки:

Первое и последнее звенья фигуры имеют по одной точке, которую они не делят с другими звеньями, а все остальные точки являются одновременно концом одного отрезка и началом другого, поэтому количество точек ломаной линии всегда на одну больше числа составляющих её отрезков.

Сравнение отрезков

Сравнить два отрезка — это значит сделать вывод о том, одинаковы ли они, или один по размеру больше другого.

Если наложить один отрезок на другой и они совпадут — это значит, что фигуры равны.

Наложение не всегда является возможным, поэтому для сравнения размеров отрезков вы можете использовать циркуль или линейку.

Отрезок: разные значения слова

Обратите внимание, что отрезок — это не только математическое понятие, хотя наибольшее распространение получило именно в этой точной науке.

Часто слово употребляется для характеристики временного промежутка — «отрезок времени»

Так же вы можете услышать словосочетание — «отрезок пути». Эта фраза обозначает расстояние — составную часть путешествия. Суть слова «отрезок» — ограничение какого-либо понятия, которое подлежит измерению.

Источник

нулевой отрезок

Смотреть что такое «нулевой отрезок» в других словарях:

Нулевой год — Это статья об ошибочной нумерации лет в календаре, см. также статью о числе 0. Нулевой год не существует согласно григорианскому или юлианскому летоисчислению. Его упоминание связано с расчётом лет согласно номерам целых чисел на координатной… … Википедия

Направленный отрезок — Под направленным отрезком в геометрии понимают упорядоченную пару точек, первая из которых точка A называется его началом, а вторая B его концом. Содержание 1 Определение … Википедия

Транслёр — Отрезок транслорного рельса. Транслёр (или Транслор; англ. Translohr) трамвай на шинах, использующий усовершенствованное крепление к единственному рельсу. Разработан и производится … Википедия

ДЕЛЕНИЕ ШКАЛЫ — отрезок шкалы между двумя соседними градуировочными отметками на аналоговой шкале. Д. ш. используется как единица счета для выражения показаний. При этом принимается во внимание, что индикаторная метка (указатель) начиная от нулевой отметки… … Энциклопедический словарь по психологии и педагогике

Вектор (математика) — Вектор У этого термина существуют и другие значения, см. Вектор … Википедия

ЭРГОДИЧЕСКАЯ ТЕОРИЯ — Введение Э. т. (метрическая теория динамических систем) раздел теории динамических систем, изучающий их статистич. свойства. Возникновение Э. т. (1 я треть 20 в.) было стимулировано попытками доказать эргодическую гипотезу (термин введён П. и Т.… … Физическая энциклопедия

ГОСТ Р 50779.10-2000: Статистические методы. Вероятность и основы статистики. Термины и определения — Терминология ГОСТ Р 50779.10 2000: Статистические методы. Вероятность и основы статистики. Термины и определения оригинал документа: 2.3. (генеральная) совокупность Множество всех рассматриваемых единиц. Примечание Для случайной величины… … Словарь-справочник терминов нормативно-технической документации

ВЕКТОР — В физике и математике вектор это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент,… … Энциклопедия Кольера

ГОСТ Р 50030.5.1-2005: Аппаратура распределения и управления низковольтная. Часть 5. Аппараты и коммутационные элементы цепей управления. Глава 1. Электромеханические аппараты для цепей управления — Терминология ГОСТ Р 50030.5.1 2005: Аппаратура распределения и управления низковольтная. Часть 5. Аппараты и коммутационные элементы цепей управления. Глава 1. Электромеханические аппараты для цепей управления оригинал документа: (обязательное)… … Словарь-справочник терминов нормативно-технической документации

В Америке есть таланты (сезон 3) — Производство NBC Ведущий(е) Джерри Спрингер Страна производства США Судьи Дэвид Хасселхофф Пирс Морган Шэрон Осборн Количество выпусков В Америке есть таланты … Википедия

МАГНИТЫ И МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА — Простейшие проявления магнетизма известны очень давно и знакомы большинству из нас. Однако объяснить эти, казалось бы, простые явления на основе фундаментальных принципов физики удалось лишь сравнительно недавно. Существуют магниты двух разных… … Энциклопедия Кольера

Источник

Что такое отрезок

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Одним из понятий геометрии, с которым знакомятся еще в начальной школе, является отрезок. Уйма задач по математике и геометрии строится на понятиях отрезка и прямой.

Понимание, что такое отрезок, поможет решать всевозможные задачи и примеры на уроках математики как в школе, так и в высших учебных заведениях.

Отрезок — это геометрическая фигура

Согласно определению в словаре, отрезком называют часть прямой, ограниченную двумя точками, находящимися на ней. Именно по обозначениям этих точек и дается название отрезка.

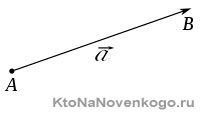
На рисунке, изображенном ниже, показан отрезок AB. Точки A и B являются концами отрезка. Длиной отрезка называют расстояние между его концами.

В математике принято обозначать точки, и соответственно отрезки, большими буквами латинского алфавита. Если нужно нарисовать отрезок, чаще всего его изображают без прямой, а лишь от одного конца до другого.

Также можно сказать, что отрезок — это совокупность всех точек, которые лежат на одной прямой и находятся между двумя заданными точками, которые являются концами данного отрезка.

Если на отрезке между его концами отметить еще одну точку, она разделит данный отрезок на два. Длину отрезка АВ можно посчитать, просуммировав длины отрезков АС и СВ.

Разница между отрезком, лучом и прямой

Школьники иногда путают понятия прямой, луча и отрезка. И вправду, эти понятия очень схожи между собой, однако имеют принципиальное различие:

Точка, находящаяся на прямой, делит ее на два луча. Количество же отрезков на одной прямой может быть бесконечным.

Чтобы различать эти фигуры на рисунке, в начале и конце рисуемой линии ставятся или не ставятся точки. Рисуя луч, точка ставится в одном конце, а изображая отрезок — в обоих концах. Прямая не имеет концов, поэтому точки в конце линии не ставятся.

Направленный отрезок — это вектор

Отрезки бывают двух видов:

Для ненаправленных отрезков, АВ и ВА — одинаковые отрезки, так как направление не имеет значения.

Если же говорить о направленных отрезках, порядок перечисления его концов имеет решающее значение. В таком случае, АВ ➜ и ВА ➜ — разные отрезки, так как они противоположно направленные.

Направленные отрезки называются векторами. Векторы могут обозначаться как двумя заглавными буквами латинского алфавита со стрелочкой над ними, так и одной маленькой буквой со стрелочкой.

Векторы часто рассматривают в системе координат. Модуль вектора равен квадратному корню суммы квадратов координат концов вектора.

Коллинеарными векторами называются те, что лежат на одной или на параллельных прямых.

Ломаная линия — это множество соединенных отрезков

Ломаная линия состоит из множества отрезков, которые называются ее звеньями. Эти отрезки соединены друг с другом своими концами и не расположены под углом 180°.

Вершинами ломаной являются следующие точки:

Число вершин ломаной всегда на один больше, чем количество ее звеньев. Обозначается ломаная перечислением всех ее вершин начиная с одного конца и заканчивая другим.

Например, ломаная ABCDEF состоит из отрезков AB, BC, CD, DE и EF и вершин A, B, C, D, E и F. Звенья AB и BC являются смежными, так как имеют общий конец — точку В. Длина ломаной вычисляется как сумма длин всех ее звеньев.

Любая замкнутая ломаная является геометрической фигурой — многоугольником.

Сумма углов многоугольника кратна 180° и вычисляется по следующей формуле 180*(n-2), где n — количество углов или отрезков, составляющих данную фигуру.

Отрезок времени

Интересно, что слово отрезок применимо не только к геометрическим понятиям, но и как временной термин.

Отрезком времени называют период между двумя событиями, датами. Он может измеряться как секундами или минутами, так и годами или даже десятилетиями.

Время в целом в таком случае определяется как временная прямая.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (2)

Чтобы не путать с лучом, надо просто запомнить, что отрезок — это две точки. То есть эта прямая и на ней две точки — это и называется отрезком.

Это самая простая часть геометрии и надо просто внимательно читать.

Жизнь тоже можно разделить на отрезки и все они будут неотделимо связаны с временем и конкретным человеком.

Источник

Вычислительная геометрия, или как я стал заниматься олимпиадным программированием.Часть 1

Здравствуйте, уважаемые хабравчане! Это моя вторая статья, и мне хотелось бы поговорить о вычислительной геометрии.

Немного истории

Я являюсь студентом уже 4 курса математического факультета, и до того как я начал заниматься программированием, я считал себя математиком на 100 процентов.

В конце первого курса мой преподаватель по информатике, который занимается олимпиадным программированием, обратил на меня внимание. Им как раз не хватало одного математика в команду. Так потихоньку меня начали приучать к олимпиадному программированию. Скажу честно, для меня это было очень сложно: для человека, который узнал слово Delphi на первом курсе. Однако мой преподаватель оказался очень грамотным специалистом и нашел хороший подход ко мне. Он начал давать мне математические задачи, который я сначала решал чисто математически, а уже потом писал код (с грехом пополам).

Мне очень нравится подход моего преподавателя: «разберись с этой темой, а потом расскажи нам, да так чтоб мы все поняли».

Итак, первой на самом деле важной задачей, с которой мне поручили разобраться, было именно вычислительная геометрия, необходимо было разобраться в типичных задач этого раздела информатики. И я решил подойти к этой задаче со всей ответственностью.

Я помню, как долго мучился с этими задачами, чтобы они прошли все тесты на сайте informatics.mccme. Зато теперь я очень рад, что прошел через все испытания и знаю, что же такое задачи вычислительной геометрии.

Вступление

«Вычислительная геометрия – это раздел информатики, изучающий алгоритмы решения геометрических задач. Такие задачи возникают в компьютерной графике, проектировании интегральных схем, технических устройств и др. Исходными данными в такого рода задачах могут быть множество точек, набор отрезков, многоугольники и т.п. Результатом может быть либо ответ на какой-то вопрос, либо какой-то геометрический объект».

Поскольку статья является достаточно большой я решил разбить ее на две части: первая часть посвящена многоугольникам, вторая – взаимному расположению различных геометрических объектов.

Немного теории о векторах

Отрезок, для которого указано, какой из его концов считается началом, а какой — концом, называется вектором. Любая точка пространства также может рассматриваться как вектор. Такой вектор называется нулевым. Начало и конец нулевого вектора совпадают, и он не имеет какого-либо определенного направления.

Длиной ненулевого вектора AB называется длина отрезка AB. Длина нулевого вектора считается равной нулю.
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Если два ненулевых вектора AB и CD коллинеарны и если при этом лучи AB и CD сонаправлены, то векторы AB и CD называются сонаправленными, а если эти лучи не являются сонаправленными, то векторы AB и CD называются противоположно направленными. Нулевой вектор принято считать сонаправленным с любым вектором.

Скалярное произведение векторов

Скалярное произведение векторов — это число, равное произведению длин этих векторов на косинус угла между ними.
(a, b) = |a||b|cos∠(a, b)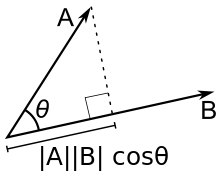

Если векторы заданы своими координатами a(x₁, y₁), b(x₂, y₂) то скалярное произведение (a, b) = x₁x₂ + y₁y₂.

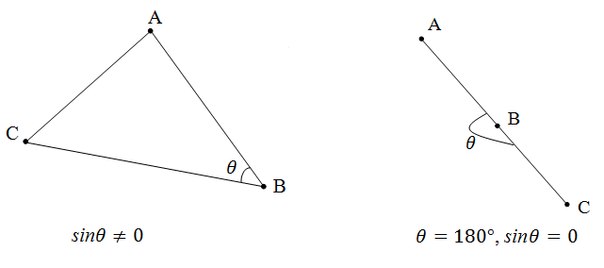
Косое произведение векторов

Псевдоскалярным или косым произведением векторов на плоскости называется число
[a, b] = |a||b|sinθ
где — угол вращения (против часовой стрелки) от a к b. Если хотя бы один из векторов a и b нулевой, то полагают [a, b] = 0.
Если векторы заданы своими координатами a(x₁, y₁), b(x₂, y₂) то косое произведение [a, b] = x₁y₂ — x₂y₁.
Геометрически косое произведение векторов представляет собой ориентированную площадь параллелограмма, натянутого на эти вектора.

Косое произведение векторов в задачах вычислительной геометрии занимает такое же почетное место, как рекурсии в комбинаторике. Это своего рода жемчужина вычислительной геометрии. Практически каждая задача вычислительной геометрии имеет более простое решение с помощью косового произведение вместо лобового решения.

А теперь займемся практикой

Начнем с треугольников

Задача №1

Задача очень простая, а именно: по введенным трем числам a, b, c определить существует ли треугольник с такими сторонами.

Решение
Понятно, что здесь нужно только проверить неравенство треугольника: a + b > c, a + c > b, b + c > a. Интересно, при изучении неравенства треугольника только ли у меня возник вопрос: не могут ли отрицательные числа тоже удовлетворять этим трем неравенствам? Оказывается, нет! Если мы сложим каждое неравенство, то получим a > 0, b > 0, c > 0. Поэтому неравенство треугольника является необходимым и достаточным условием существования треугольника.

Задача №2

Задача является очень похожей на предыдущую с той разницей, что треугольник задан не сторонами, а координатами вершин.

Решение
С первого взгляда решение кажется очевидным: вычислить стороны треугольника и свести задачу к предыдущей. Однако поскольку расстояние между двумя точками A(x₁, y₁), B(x₂, y₂) вычисляется по формуле √(x₁-x₂) 2 +(y₁-y₂) 2 то при извлечении корня возможна потеря точности, что плохо скажется на проверке неравенства треугольника. Оказывается, что если треугольник задан координатами своих вершин, то вычислять длины его сторон и проверять неравенство треугольника не требуется. В этом случае треугольника не существует тогда и только тогда, когда данные три точки лежат на одной прямой. А это легко проверяется через косое произведение векторов. Если оно равно нулю, то векторы коллинеарные, то есть все три точки лежат на одной прямой.

Во всех следующих задачах будем считать, что треугольник существует, поскольку процедуру проверки существования треугольника мы только что рассмотрели.

Задача №3

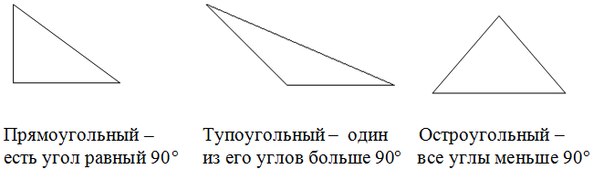
Треугольник задан своими сторонами. Определить тип треугольника: тупоугольный, прямоугольный или остроугольный.

Решение
Вспомним, что представляют собой каждый вид треугольника.

Задача №4

Задача аналогична предыдущей задаче, только треугольник задан не своими сторонами, а координатами вершин.

Решение
Аналогично задаче 2 можно сказать, что эта задача полностью сводится к предыдущей задаче (так оно и есть). Однако, как и во второй задаче, решение можно упростить. Вообще, если треугольник задан координатами своих вершин, то всегда легче работать с ним через вектора, нежели вычислять стороны. Аналогично предыдущей задаче, необходимо определить каким является наибольший из углов треугольника. Вид угла легко определяется по знаку скалярного произведения образующих его векторов: оно положительно для острого угла, равно нулю для прямого угла и отрицательно для тупого угла. Поэтому необходимо посчитать все три скалярных произведения и перемножить их и по знаку данного числа можно судить о типе треугольника.

Задача №5

По данным сторонам треугольника найти его площадь.

Решение
Очевидно решение, заключается в применение формулы Герона.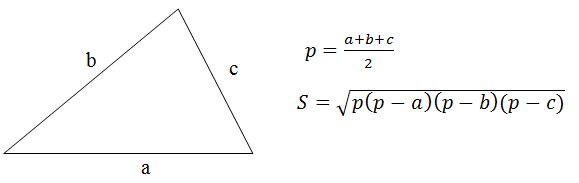

Кстати, никого не интересовало доказательство этой формулы?

Задача №6

Вычислить площадь треугольника заданного координатами своих вершин.

Решение
Не будем говорить о решении, которое сводится к предыдущей задачи, а попробуем воспользоваться геометрическим смыслом косового произведения. Геометрически косое произведение двух векторов определяет ориентированную площадь параллелограмма натянутого на эти вектора. Поскольку диагональ параллелограмма разбивает его на два равновеликих треугольника, то можем найти площадь нашего треугольника, как половину площади параллелограмма.
Для векторов a(x₁, y₁), b(x₂, y₂)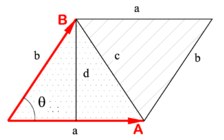

S = (x₁y₂ — x₂y₁) / 2 — ориентированная площадь треугольника

Задача №7

Дана точка и треугольник заданный координатами своих вершин. Определить лежит ли точка внутри, на границе или вне этого треугольника.

Решение
У этой задачи есть два принципиально разных решения. Начнем с наименее привлекательного.

Метод площадей

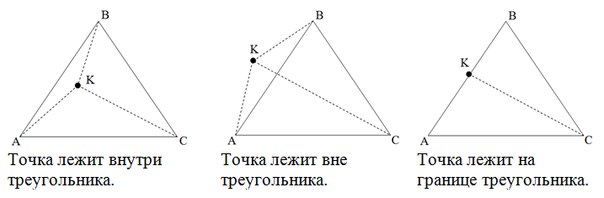
Если сумма площадей треугольников AKB, AKC, BKC (не ориентированных, а «обычных») больше площади треугольника ABC точка лежит вне треугольника. Если же сумма первых трех площадей равна четвертой, то нужно проверить, не равна ли нулю одна из трех площадей. Если равна, то точка лежит на границе треугольника, иначе – внутри.
Вычислять площади треугольников, естественно, надо через косое произведение векторов. Этот метод не очень хороший. Поскольку здесь используются сравнение чисел с плавающей точкой, а это в свою очередь может привести к принятию неверного решения при сравнении. Второй метод опять таки опирается на вектора, он намного эффективнее во всех отношениях.

Проверка полуплоскостей

Если хотя бы одна из сторон треугольника «разводит» противолежащую ей вершину и точку по разным полуплоскостям, то точка лежит вне треугольника. Иначе, если точка принадлежит хотя бы одной из прямых, содержащих стороны треугольника, то она находится на границе треугольника. Иначе точка лежит внутри треугольника.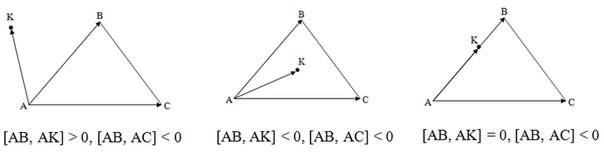

В первом примере сторона AB разводит вершину C и точку K по разным полуплоскостям, поэтому точка лежит снаружи.

Задача №8

Вычисление площади многоугольника заданного координатами своих вершин.

Решение
Под многоугольником будем подразумевать простой многоугольник, то есть без самопересечений. При этом он может быть как выпуклым, так и не выпуклым.

Данную задачу можно решить двумя способами: вычисляя ориентированные площади трапеций и треугольников.

Метод трапеций

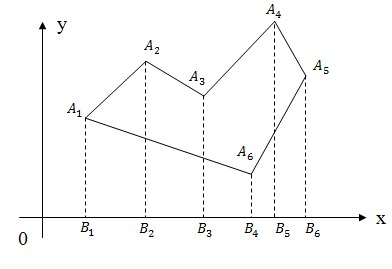
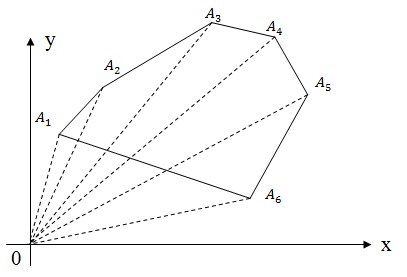
Для того чтобы посчитать площадь многоугольника нужно разбить его на трапеции, так как это показано на рисунке, а затем сложить ориентированные площади полученных трапеций это будет ориентированной площадью исходного многоугольника.
S = S_{A1 A2 B2 B1} + S_{A2 A3 B3 B2} + S_{A3 A4 B5 B3} + S_{A4 A5 B6 B5} + S_{A5 A6 B4 B6} + S_{A6 A1 B1 B4}
Площади трапеций считаем по известной формуле: полусумма оснований на высоту
S_{A1 A2 B2 B1} = 0.5 * (A₁B₁ + A₂B₂) *(B₂ — B₁)

Поскольку полученная площадь является ориентированной, необходимо вычислить ее модуль.

Метод треугольников

Как вы видите задача вычисления площади многоугольника достаточна проста. Не знаю, почему, но мне больше нравится решать эту задачу методом разбиения на трапеции (наверно потому, что на всех олимпиадах я ее так решал). Тем более, что при втором решении площади треугольников надо вычислять через косое произведение. О формуле Герона надо забыть.

Задача №9

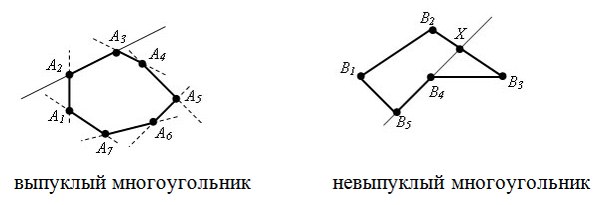
Многоугольник задан координатами своих вершин в порядке его обхода. Необходимо проверить является ли многоугольник выпуклым.

Решение
Напомню, что многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону.

Задача опять сводится к вычислению косового произведения векторов, а именно у выпуклого многоугольника знаки косых произведений [A_i A_i+1, A_i+1 A_i+2] либо положительны, либо отрицательны. Поэтому если мы знаем направление обхода, то знак косых произведений для выпуклого многоугольника одинаков: он неотрицателен при обходе против часовой стрелки и неположителен при обходе по часовой стрелки.

Задача №10

Многоугольник (не обязательно выпуклый) на плоскости задан координатами своих вершин. Требуется подсчитать количество точек с целочисленными координатами, лежащих внутри него (но не на его границе).

Решение
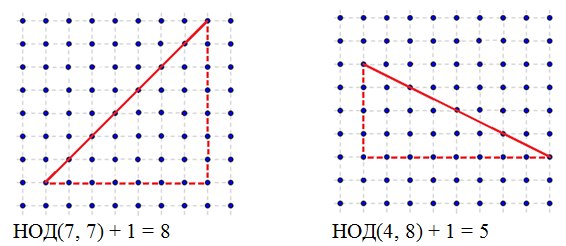
Для решения этой задачи рассмотрим вспомогательную задачу: отрезок задан координатами своих концов, являющихся целыми числами. Необходимо посчитать количество целочисленных точек лежащих на отрезке. Понятно, что если отрезок вертикальный или горизонтальный, то необходимо вычесть координаты концов и добавить единицу. Интерес представляет случай, когда отрезок не является вертикальным или горизонтальным. Оказывается в этом случае необходимо достроить отрезок до прямоугольного треугольника и ответом будет число равное наибольшему общему делителю длин катетов этого треугольника плюс единица.

Для любого многоугольника с целочисленными координатами вершин справедлива формула Пика: S = n + m/2 — 1, где S – площадь многоугольника, n – количество целых точек лежащих строго внутри многоугольника, m – количество целых точек лежащих на границе многоугольника. Поскольку площадь многоугольника мы знаем как вычислять, то S известно. Так же мы можем вычислить количество целых точек лежащих на границе многоугольника, поэтому в формуле Пика остается лишь одна искомая неизвестная которую мы можем найти.
Рассмотрим пример: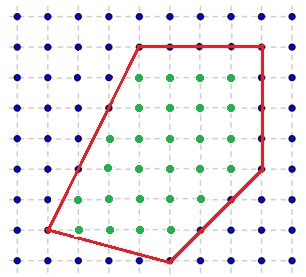

S = 16 + 4 + 4,5 + 6 + 1 + 2 = 33,5
m = 15
n = 33,5 – 7,5 +1 = 27 — точек лежит строго внутри многоугольника
Вот так вот решается эта задачка!

Вот и все! Надеюсь, Вам понравилась статья, и я напишу ее вторую часть.

Источник