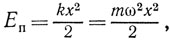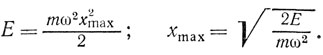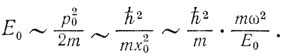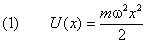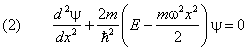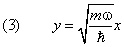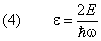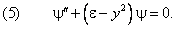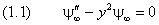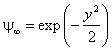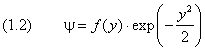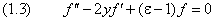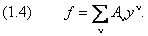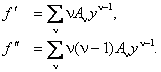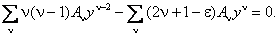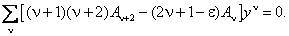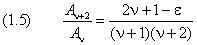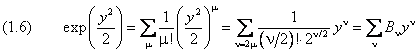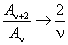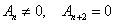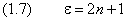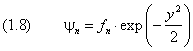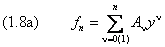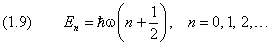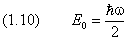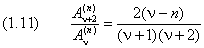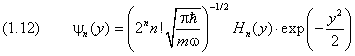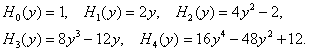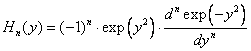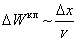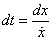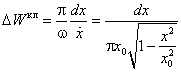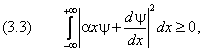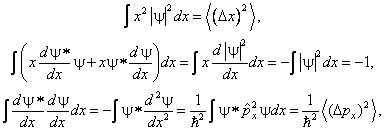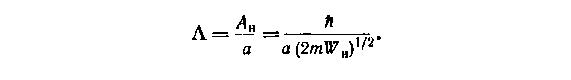Что такое нулевые колебания как объяснить наличие нулевых колебаний

Речь идет о тех колебаниях атомов кристаллической решетки, которые происходят тогда, когда температура кристалла становится равной нулю.

Различают нулевые колебания вакуума и нулевые колебания атомов конденсированной среды, устанавливающиеся после «выморожения» нормальных тепловых колебаний кристаллической решётки. Считается, что нулевые колебания атомов устанавливаются при абсолютном нуле температур. Таким образом, энергия нулевых колебаний есть ничто иное как энергия основного состояния системы. Энергия одного нулевого колебания атома равна

E0 = hν, где h — постоянная Планка, ν — частота нулевого колебания.

Этой же формулой определяется и энергия нулевых колебаний физического вакуума. Суммарная энергия нулевых колебаний конечного объема физического вакума или конденсированной среды огромна, однако с точки зрения квантовой механики ее невозможно практически использовать, поскольку нет квантовомеханических способов отнять всю или часть энергии у нулевого колебания. С точки зрения теоремы Нернста энтропия нулевых колебаний должна быть равна нулю, поскольку это чрезвычайно упорядоченное движение атомов. С точки зрения квантовой термодинамики нулевые колебания атомов устанавливаются при температуре несколько выше температуры абсолютного нуля, это значение температуры конденсированного состояния вещества, в котором выморожены тепловые колебания, равно

T0 = hν / k, где k — постоянная Больцмана.

PS Что то уже не воспринимается что написано

Источник

Нулевые колебания. Часть 1

Но обратимся к принципиальной стороне вопроса. Откуда вообще берется энергия вакуума? Наличие некоторой конечной энергии в основном состоянии физических систем непосредственно следует из самих основ квантовой теории, в квантовой физике на этот счет имеются основательные соображения. Отсутствие такой энергии означало бы, что точно задан как импульс объекта (равный нулю), так и его координата, которая в этом случае соответствовала бы точке минимума потенциальной энергии. Однако возникновение такой ситуации противоречит одному из базовых постулатов квантовой механики — принципу неопределенности Гейзенберга, т. е. для любых финитных систем должно существо-

вать по крайней мере одно квантовое состояние, реализующее минимум функционала полной энергии системы. Известно, что соотношение неопределенности позволяет оценить, с точностью до некоторого числового множителя, энергию любой финитной квантовой системы, в частности, наинизшая энергия квантового осциллятора не равна нулю, она составляет величину ш/2. Из этих «нулевых колебаний», как их называют, и складывается ненулевая энергия наинизшего энергетического состояния квантовых полей. Таков принципиальный ответ на вопрос о природе энергии квантового вакуума. Но реально подсчитать соответствующую суммарную плотность энергии, связанную с нулевыми колебаниями, квантовая теория поля (как мы уже замечали) не позволяет. Если рассмотреть ансамбль квантовых осцилляторов в качестве модели физических полей и суммировать энергию нулевых колебаний по всем возможным частотам вплоть до бесконечности, то результатом и будет бесконечная энергия и бесконечная плотность энергии вакуума.

Чтобы избежать таких расходимостей, прибегают к ограничению диапазона частот сверху на некотором значении частоты, которое принимается за предельное. Можно, например, считать, что предельной частоте отвечает планковская энергия Мр\, так что k>max

Мр\. Аргументом в пользу подобного выбора предельной частоты служит тот несомненный факт, что для энергий, превышающих планковскую, стандартные представления физики, в том числе и само понятие частоты, теряют обычный смысл. Но получающаяся при таком подходе плотность вакуума, как можно видеть (хотя бы из соображений размерности), равна по порядку величины четвертой степени частоты, и следовательно, она будет иметь значение

рр\, которое, как мы видели, на сто с лишним порядков величины отличается от реального.

Кроме того, необходимо учитывать и неопределенности в энергии нулевых колебаний [46], связанные как с линейной связью рассматриваемой системы с внешним миром, так и с нелинейной связью (в частности, для гармонического осциллятора энергия нулевых колебаний зависит от частоты осциллятора, которая, в свою очередь, зависит от внешних условий, например, наличия трения [83]). Как следствие, у рассматриваемой системы всегда есть тепловые и фундаментальные квантовые неопределенности, вследствие чего становится неопределенной частота резонатора и, соответственно, энергия его нулевых колебаний, причем такие эф-

Источник

Что такое нулевые колебания как объяснить наличие нулевых колебаний

Нулевые колебания

Отсюда следует, что амплитуда колебания х_mak связана с запасом энергии тела Е формулой

Но амплитуда колебаний на квантовом языке как раз определяет характерный размер области локализации частицы, который в силу соотношения неопределенностей связан с минимальным импульсом частицы. Получается, с одной стороны, чем меньше энергия колебаний, тем меньше должна быть амплитуда; с другой стороны, уменьшение амплитуды приводит к увеличению импульса, а следовательно, и энергии частицы. Минимальная энергия, которой может обладать частица, определяется из оценки

Сравнивая здесь первое и последнее выражения, находим E₀

ћω. Точный расчет дает вдвое меньшее значение. Энергия нулевых колебаний равна ћω/2. Она максимальна у легких атомов, которые колеблются с большей частотой.

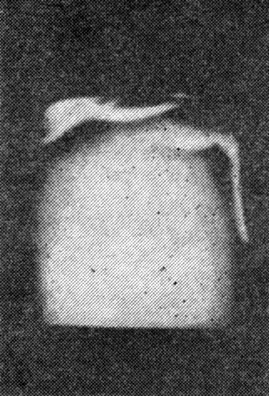
Рис. 4. Волны на границе между твердым (светлая область) и жидким гелием

При давлении около 25 атмосфер жидкий гелий все-таки затвердевает. Твердый гелий, правда, тоже не совсем кристалл. В нем нулевые колебания определяют, например, кинетическую энергию атомов на границе между твердым и жидким гелием, и вследствие этого поверхность кристалла может совершать гигантские колебания, словно граница между двумя неперемешивающимися жидкостями (рис. 4). Твердый гелий физики назвали квантовым кристаллом, и его свойства сейчас интенсивно исследуются.

Источник

Что такое нулевые колебания как объяснить наличие нулевых колебаний

Линейным гармоническим осциллятором называется система, потенциал ьная энерги я которой квадратично зависит от координаты:

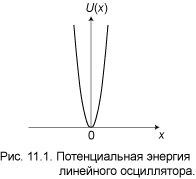
Здесь m — масса частицы, а ω — собственная частота осциллятора. На рис. 11.1 зависимость (1)

изображена графически. Кривая U ( x ) своей крутизной и бесконечно большой высотой напоминает потенциал ьную яму. Ниже мы увидим, что линейный осциллятор, действительно, проявляет некоторые свойства частицы в бесконечно высокой потенциал ьной яме. Например, он имеет бесконечное число дискретных уровней. Но в отличие от отвесных стенок ямы, потенциал осциллятора растёт плавно, и, как следствие, появляется некоторая вероятность обнаружить частицу достаточно далеко от начала координат. Плавная форма потенциал а позволяет осциллятору при определённых условиях проявить свойства классической (не квантовой) частицы. Для этого достаточно, чтобы длина волны де Бройля была меньше характерных размеров области изменения потенциал а. В случае потенциал ьной ямы, либо потенциал ьного барьера, такая возможность полностью исключена, так как там потенциал меняется скачком в одной точке. Перейдём к количественному решению задачи.

Напишем одномерное уравнение Шредингера с потенциал ьной энерги ей (1):

У него нет естественных граничных условий. Дискретные уровни энерги и получаются как следствие ограниченности волновой функции.

Преобразуем уравнение (2): вместо координаты x введём безразмерный аргумент

и вместо E — безразмерную энерги ю осциллятора

Квантовые свойства осциллятора имеют многочисленные приложения в атомной физике. Ниже мы рассмотрим два из них: влияние нулевых колебаний электромагнитного вакуума на функцию Планка и связанный с ними лэмбовский сдвиг метастабильного уровня атома водорода.

11.1 Решение волнового уравнения

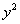
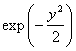
Множитель перед функцией появляется при двукратном дифференцировании экспоненты , а именно:

В области больших значений аргумента можно пренебречь единицей по сравнению с y 2 в множителе 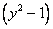. Следовательно, рассматриваемая экспонента может служить асимптотическим приближением точного решения:

Решение уравнения (5) при произвольных значениях аргумента будем искать в виде

Согласно (5), функция f ( y ) удовлетворяет уравнению

Ищем решение в виде ряда:

Дважды продифференцируем искомую функцию

Подставив эти разложения в (1.3), получим бесконечную цепь линейных уравнений для коэффициентов разложения A _ν :

Соберем степени с одинаковыми показателями, для чего индекс первой суммы увеличиваем на два:

Здесь ν принимает только чётные значения. Мы ввели обозначение

Теперь ясно, что функция, описываемая соотношением (1.5), растёт быстрее, чем экспонента (1.6). Следовательно, произведение (1.4) при больших значениях аргумента неограниченно возрастает. Поэтому физический смысл имеет только такое решение (1.3), в котором сумма (1.4) содержит лишь конечное число слагаемых.

Покажем, как требование конечности числа слагаемых приводит к дискретному спектру энергетических уровней осциллятора. Пусть n — номер последнего члена ряда (1.4), не равного нулю:

Из (1.5) вытекает связь между величиной энергетического уровня и его номером:

Итак, мы снова получили дискретные уровни энерги и. Каждому уровню с номером n соответствует ровно одна волновая функция:

причём нижний предел равен нулю при чётном n и единице — при нечётном. Уровни энерги и, согласно (4) и (1.7), принимают дискретный ряд значений:

Обратим внимание на то, что наименьшее из возможных значений энерги и, равное

Рекуррентное соотношение (1.5) с учётом (1.7) принимает вид

Приведём несколько первых полиномов Эрмита:

Исследуем полученное решение.

11.2 Свойства квантового осциллятора

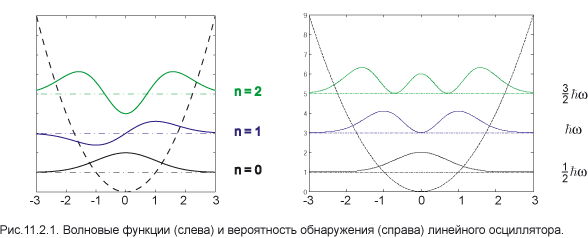
Парабола изображает потенциал ьную функцию, а горизонтальные прямые — значения энергетических уровней. Для удобства восприятия волновые функции сдвинуты по вертикальной оси.

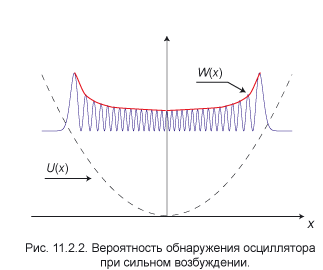
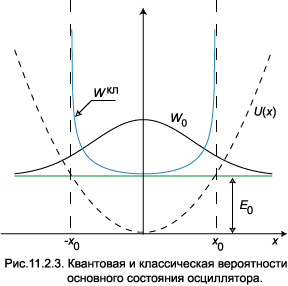
В состояниях с сильным возбуждением квантовый осциллятор приобретает свойства классической частицы. На рис. 11.2.2 схематически изображён график вероятности в

В точках поворота скорость обращается в нуль, поэтому там легче всего найти частицу. В самом деле, рассмотрим движение частицы по закону

Классическую вероятность обнаружения частицы на отрезке от x до x + dx определим как отношение времени прохождения отрезка

к половине периода колебаний:

обозначает уровень нулевых колебаний E ₀ из (1.10). Классическая вероятность увеличивается по мере приближения к точке x ₀, определяемой условием U ( x ₀) = E ₀, но не может перейти через эту границу. Квантовая теор ия предсказывает уменьшение вероятности при приближении к границе, причём частица может быть обнаружена в классически недоступной области x > x ₀.

11.3. Нулевые колебания

В самом низком состоянии осциллятор имеет отличную от нуля энерги ю (1.10), определяемую его собственной частотой. Нулевые колебания осциллятора имеют чисто квантовую природу и находят своё объяснение в соотношении неопределённостей. Полная энерги я осциллятора равна сумме кинетической и потенциал ьной

.

.

.

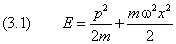
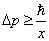
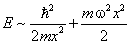
Полная энерги я как функция x имеет минимум в точке

,

.

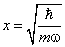
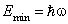
Полученное значение в два раза отличается от результата точного расчёта. Это не удивительно, так как соотношение неопределёностей даёт оценки лишь по порядку величины. Точное выражение для энерги и нулевых колебаний получается из упомянутого в главе неравенства для дисперсий момента и координаты:

,
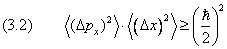
Формально она выводится следующим образом. Пусть состояние частицы описывается функцией y ( x ), причём средние значения импульса и координаты для простоты вывода предполагаются равными нулю. Напишем очевидное неравенство

где a — действительная постоянная. Далее вычислим три полезных выражения:

Они позволяют преобразовать левую часть (3.3) в квадратичный по a трёхчлен:

Источник

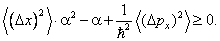
НУЛЕВЫЕ КОЛЕБАНИЯ

НУЛЕВЫЕ КОЛЕБАНИЯ

Вначале о термине «нулевые колебания». Речь идет о тех колебаниях атомов кристаллической решетки, которые происходят и тогда, когда температура кристалла становится равной нулю. Они происходят и при иной, более высокой температуре, одновременно с обычными, классическими колебаниями, которые при нулевой температуре должны замереть. Классические замирают, а нулевые, или квантовые, остаются в чистом виде. Они не чувствительны к температуре! Они неуничтожаемы! Они — непременный признак жизни кристалла.

Если читателю совершенно неизвестны элементарные квантовые представления, буду его просить на начальном этапе наших рассуждений просто поверить мне, а я буду добросовестным и злоупотреблять доверием не стану. Впрочем, в очерке о теории Эйнштейна и Дебая я уже молчаливо пользовался доверием читателя, обсуждая свойства квантового маятника.

Здесь мне надо воспользоваться законом, который в конце 20-х годов сформулировал один из создателей квантовой механики немецкий физик Вернер Гейзенберг. Этот закон часто называют «принципом неопределенности». Речь идет вот о чем. Согласно принципу неопределенности для какой-либо частицы нельзя одновременно абсолютно точно определить координату х и импульс р х , направленный вдоль оси х. И та, и другая величины могут быть найдены с некоторой неточностью, при этом произведение этих неточностей обязательно превосходит величину постоянной Планка h, деленную на 2?:

Откуда следует это утверждение? Оно — изначальный, фундаментальный закон природы, которая устроена так, а не иначе. Оно, говоря философскими терминами, отражение объективной реальности. Вопрос «откуда» в данном случае задавать не следует, как не следовало спрашивать, почему энергия маятника квантуется. Впрочем, и принцип неопределенности, и квантование энергии маятника — это две стороны одного и того же закона природы. И Планк, и Эйнштейн, и Гейзенберг потому и велики, что сумели, наблюдая природу, подсмотреть или выпытать у нее фундаментальные законы, которые природа соблюдает. Или, быть может, догадаться о них, почувствовать, что они должны существовать.

То обстоятельство, что импульс атома в узле кристаллической решетки, т. е. в той позиции, где в соответствии со структурой кристалла атом расположен, не может быть равен нулю (потому что нуль — величина точная, а импульс может определяться с некоторой неточностью!), означает, что атом должен двигаться, а так как факт существования кристалла означает, что атом должен находиться неподалеку от узла решетки и, следовательно, ему не позволено смещаться на неограниченные расстояния, то его движение должно быть колебательным.

Итак, один из непременных признаков жизни кристалла — нулевые колебания составляющих его атомов. Нам, живущим в мире «нормальных условий» и «классических» проявлений законов природы, легко воспринять факт существования тепловых колебаний: более высокая температура — колебания активнее, при определенной температуре колебания могут стать настолько активными, что кристалл будет вынужден расплавиться. Тепловые колебания — еще со школьных лет явление настолько привычное, что кажется понятным и тогда, когда истинного понимания нет. Привычное, как правило, не вызывает вопросов, а, следовательно, молчаливо предполагается понятным. А вот нулевые колебания — за пределами привычного. Приблизимся к ним, попытаемся освоиться с ними, оценить величины, которые характеризуют этот вид колебаний.

Вначале о частоте нулевых колебаний. Здесь все ясно: она та же, что и при тепловых колебаниях. Иной она быть не может, так как вне зависимости от причины, вызывающей колебания, атом колеблется в определенной среде, обладающей определенными свойствами. Характеристики среды и атома и определяют частоту его колебаний. Эту частоту легко вычислить, так как ранее мы уже находили ? 0:

Теперь об энергии нулевых колебаний W н. Как следует из квантовой механики (поверьте!),

Видимо, читатель хочет спросить: где источник этой энергии нулевых колебаний, которые существуют всегда, пока кристалл есть кристалл, за счет какого горючего она сохраняется? Сегодня не следует этого спрашивать! Нет такого горючего! Эта энергия — необходимое условие существования вещества, ее нельзя позаимствовать у данного вещества и перенести в другое. Философ, со свойственной ему склонностью к трудным словам, сказал бы так: она — непременный атрибут материи, она — форма существования материи, она существует, поскольку существует материя. Мы уже не первый раз встречаемся с тем, что не любая фраза, завершающаяся вопросительным знаком, формулирует вопрос, на который можно и нужно отвечать. Вот так! А вот вопрос о том, велика или мала величина энергии W н (разумеется, по сравнению с какой-либо иной характерной энергией кристалла), — это вопрос! Его следует задать, и на него следует ответить.

W н = kТ Г, т. е. Т Г = W н /k. Легко вычислить, что Т Гн 2 = 73 К, а Т ГAu = 255 К. Кристалл водорода раньше расплавится, чем перейдет в область температур, где главенствуют тепловые колебания, а кристалл золота уже при комнатной температуре, которая ниже температуры его плавления больше, чем на тысячу градусов, окажется во власти главным образом тепловых колебаний.

Если руководствоваться самыми общими соображениями, естественно предположить, что свойства кристалла должны существенно зависеть от соотношения между двумя его характерными энергиями: нулевой и энергией связи. Верное предположение, мы будем иметь случай убедиться в этом.

Об амплитуде нулевых колебаний. Ее легко можно оценить, воспользовавшись уже известным нам соотношением, которое описывает принцип неопределенности. Неопределенности в координате ?х придадим смысл амплитуды нулевых колебаний A н, а неопределенность в импульсе ?р х близка к среднему значению импульса частицы р х, который связан с кинетической энергией нулевых колебаний: W н = р х 2 /2т. Таким образом,

Вот теперь соотношение неопределенностей можно переписать в виде

Рассуждая о нулевых колебаниях, физики часто пользуются величиной так называемого параметра де Бура. Им определяется отношение амплитуды нулевых колебаний к межатомному расстоянию:

Когда параметр де Бура существенно превосходит единицу, это означает, что вещество ни при какой температуре не может существовать в кристаллической фазе, если искусственно (приложением внешнего давления) не уменьшить амплитуду нулевых колебаний и таким образом уменьшить ? до значений порядка единицы и менее. Таким веществом, как известно, является гелий, который в обычных условиях остается жидким при сколь угодно низких температурах. Закристаллизовать его можно, лишь приложив давление. Небольшое, около 25 атмосфер. Естественно, может возникнуть вопрос, почему этим свойством не обладает водород, который, как известно, легче гелия. Дело в том, что параметр де Бура определяется не только массой атомов, но и энергией взаимодействия между ними. В случае водорода эта энергия больше, чем в случае гелия, и в этом причина того, что водород отвердевает, а гелий нет!

Мой рассказ об одном из непременных признаков жизни кристалла — о нулевых колебаниях — с самого начала основан на доверии читателя.

Доверием я не злоупотребил. Нулевые колебания себя обнаруживают во многих физических явлениях, главным образом в так называемых «квантовых кристаллах», у которых амплитуда нулевых колебаний велика, параметр ? достигает значений, превосходящих единицу. Это — кристаллы, для которых характерна малая энергия связи, и существуют они в области низких температур (ожиженные и закристаллизованные идеальные газы и др.). Благодаря активным нулевым колебаниям, эти кристаллы обладают аномальными механическими свойствами. А недавно физики обнаружили, что в кристаллах изотопов гелия вблизи 0 К происходит так называемая «квантовая диффузия», при которой коэффициент диффузии растет с понижением температуры. Удивительно? Удивительно, но факт!

Читайте также

Глава 49 СОБСТВЕННЫЕ КОЛЕБАНИЯ

Глава 49 СОБСТВЕННЫЕ КОЛЕБАНИЯ § 1. Отражение волн§ 2. Волны в огра­ниченном пространстве и собственные частоты§ 3. Двумерные собственные колебания§ 4. Связанные маятники§ 5. Линейные системы§ 1. Отражение волнВ этой главе мы рассмотрим ряд замеча­тельных явлений,

4. Тайна света: колебания в пятом измерении

4. Тайна света: колебания в пятом измерении Если она [относительность], как я предвижу, будет подтверждена, его следует считать Коперником XX в. Макс Планк об Альберте Эйнштейне История жизни Альберта Эйнштейна выглядит как длинная череда неудач и разочарований. Его мать

12. Механические колебания

12. Механические колебания Повторяющиеся движения (или изменения состояния) называют колебаниями (переменный электрический ток, явление маятника, работа сердца и т. п.). Различают:1) свободные, или собственные, колебания – такие колебания, которые происходят в отсутствие

V. Колебания

V. Колебания Равновесие В некоторых случаях равновесие очень трудно поддержать – попробуйте пройтись по натянутому канату. В то же время никто не награждает аплодисментами сидящего в кресле-качалке. А ведь он тоже поддерживает свое равновесие.В чем же разница в этих

Простые колебания

Простые колебания Если толкнуть шарик, лежащий в углублении, он начнет двигаться в гору, постепенно теряя кинетическую энергию. Когда она будет потеряна полностью, произойдет мгновенная остановка и начнется движение вниз. Теперь уже потенциальная энергия будет

Более сложные колебания

Более сложные колебания То, что говорилось до сих пор, относится к колебаниям вблизи положения равновесия, происходящим под действием возвращающей силы, величина которой прямо пропорциональна смещению точки от положения равновесия. Такие колебания происходят по закону

Звуковые колебания

Звуковые колебания Мы уже сообщили читателю много сведений о колебаниях. Как колеблется маятник, шарик на пружинке, каковы закономерности колебания струны – этим вопросам была посвящена пятая глава книги. Мы не говорили о том, что происходит в воздухе или другой среде,

Колебания черных дыр

Колебания черных дыр В 1971 году Билл Пресс, мой студент в Калтехе, обнаружил, что черные дыры могут вибрировать на особых резонансных частотах, подобно тому как это происходит со скрипичной струной.Если правильно ущипнуть струну, она издаст чистый тон – звуковую

Резонансные колебания Гаргантюа

Резонансные колебания Гаргантюа На рис. 18.1 – первая страница данных, собранных Ромилли. Каждая строчка чисел на этой странице относится к одной из резонансных частот колебаний Гаргантюа. Рис. 18.1. Первая страница данных, подготовленных Янгом и Циммерманом, чтобы

Источник