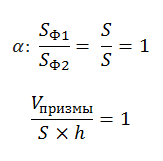Что такое объемные фигуры

Конспект занятия по ФЭМП «Объемные геометрические фигуры» в подготовительной к школе группе

Айлана Хеймер-ооловна Иргит
Конспект занятия по ФЭМП «Объемные геометрические фигуры» в подготовительной к школе группе

Конспект по ФЭМП: «Объемные геометрические фигуры» в подготовительной к школе группе.

Цель: систематизировать и закрепить математические представления детей подготовительной группы

— закреплять знания геометрических фигур, их элементов (углы, стороны);

— развивать умение группировать геометрические фигуры по цвету и форме;

— упражнять в составлении тематических композиций из геометрических фигур;

— закреплять знания объемных (куб, цилиндр, шар, конус, тор, параллелепипед, призма) и плоскостных (квадрат, треугольник, трапеция, круг, прямоугольник, овал, многоугольник) фигур.

— развивать психологические процессы: слуховое и зрительное внимание, логическое мышление, мелкую моторику рук, воображение, сообразительность;

— развивать социальные навыки: умение работать индивидуально и в коллективе, договариваться, учитывать мнение партнёра;

— развивать умения анализировать предметы сложной формы, составленных из гео-метрических фигур, и воссоздавать модель по образцу;

— развивать у детей логическое мышление, сообразительность, внимание, умение находить признаки сходства и различия.

— воспитывать личностные качества у каждого ребёнка: любознательность, целе-устремлённость, устойчивость интереса к знаниям и умениям, самостоятельность.

Материал: набор геометрических фигур разного цвета, счётные палочки, пласти-лин, набор плоскостных и объёмных фигур, мешочек с фигурами, раздаточный материал «Найди лишнюю фигуру», плакаты плоскостных и объёмных фигур.

Ход занятия.

1. Вступление. Организационный момент.

Воспитатель: Здравствуйте, ребята!

Наши умные головки

Будут думать много, ловко

Ушки будут слушать,

Ротик четко говорить,

Ножки будут топать,

Друг другу улыбаемся,

Занятие начинается.

Воспитатель: Молодцы, ребята! Сегодня на занятии мы с вами вспомним всё, что мы знаем о геометрических фигурах и узнаем новые секреты фигур. Но для того, чтобы вы быстро и правильно отвечали, надо сделать зарядку для ума. Повторение фигур (за-ранее вывешивается плакат геометрическими фигурами разной формы и разных цветов)

Воспитатель: Молодцы! Вот теперь можно приступать к более сложной работе.

— Ребята, у вас на столах у каждого есть набор геометрических фигур. Давайте по-строим дом из фигур. Ставим стену, берем квадрат. Ребята у вас получается? (ответы детей)

Воспитатель: На самом деле. Может прямоугольник может устоять? Может быть круг? Треугольник? Овал? (ответы детей)

Воспитатель: В чём же дело? Какой он тоненький. Ах, да у него же нету тела.

У меня есть тело, и у вас есть тело, можете даже постоять? (ребята встают)

На самом деле мы не падаем. Таким образом мы подводим ребят к понятию «тело».

2. Постановка цели. Геометрическое тело.

Воспитатель показывает фигуры:

Круг –шар (шар стоит, круг нет)

Квадрат – куб (у куба есть тело, а у квадрата нет). А давайте посчитаем стороны куба. Считаем с детьми.

Призма – треугольник. И катится призма не очень.

— Ребята, как называются фигуры, которые изображены на рисунке, давайте пере-числим, начиная с первой.

— Что лежит в основании цилиндра?

— Что лежит в основании конуса?

— Что лежит в основании призмы?

— Что лежит в основании куба? Прямоугольного параллелепипеда?

— А теперь вспомним, что такое грани и назовем количество граней этих фигур. (Показываю грани и считаю их вместе с детьми, демонстрируя это на объемных фигурах)

— Сколько граней у куба? Призмы? Параллелепипеда?

3. Совместная деятельность воспитателя с детьми.

Работа со счётными палочками.

Цель: развивать мелкую моторику рук, воображение, умение, воссоздавать модель по образцу;

Воспитатель: Теперь поработаем со счетными палочками.

Вам будет следующее задание: предлагается детям собрать модель куба при помощи счетных палочек и пластилина. Показываю поэтапно, как собрать куб, параллелепипед, и призму.

Если дети затрудняются, то подсказать им, или помочь выполнить задание.

4. Физминутка «Колобок»

5. Игра «Найди лишнюю фигуру».

Цель: Учить детей находить лишнюю фигуру, ориентируясь на форму (цвет и размер) фигуру, развивать смекалку, сообразительность и логическое мышление

Воспитатель: Ребята посмотрите на картинку, как вы думаете, какая из этих фигур лишняя и по какому принципу? (по цвету, форме, размеру?

7. Игра «Волшебный мешочек»

Цель: закреплять знания геометрических тел.

Воспитатель: Ребята сейчас я вам расскажу сказку.

8. Игра «Геометрический город»

Цель: закрепить знания геометрических тел, развитие мелкой моторики

Воспитатель: Теперь ребята, я, вам предлагаю из объемных геометрических фигур построить город.

Воспитатель: Ребята, вам понравилось моделировать фигуры из счетных палочек? В следующий раз мы попробуем смоделировать другую фигуру.

— Что мы сегодня с вами повторяли? (ответы детей).

— Молодцы, вы хорошо сегодня поработали!

Конспект НОД по ФЭМП в подготовительной к школе группе «Умная мастерская» Интеграция образовательных областей: «Познавательное развитие», Социально-коммуникативное развитие», «Речевое развитие», «Физическое.

Конспект НОД по ФЭМП в подготовительной к школе группе «Умная мастерская» Интеграция образовательных областей: «Познавательное развитие», «Социально-коммуникативное», «Речевое развитие», «Физическое развитие».

Конспект открытого занятия по ФЭМП в подготовительной к школе групп «Занимательная математика» Программное содержание: Цель: закрепление знаний о математических представлениях посредством игры – путешествия. Обучающие задачи: 1. Закрепить.

Конспект занятия по ФЭМП в младшей группе «Геометрические фигуры» Конспект занятия по ФЭМП в младшей группе «Геометрические фигуры» Цель: Совершенствовать умение различать и называть геометрические фигуры:.

Мастер-класс «Объемные фигуры из спичек и пластилина» для детей подготовительной группы Чтобы научить детей делать сложные объемные фигуры, начинаем с проведения занятия, на котором учим изготавливать кубы из спичек и пластилина:.

«Геометрические фигуры. Круг, квадрат». Конспект занятия по математике в младшей группе Программное содержание: 1. Учить сравнивать два предмета по форме и величине. 2. Содействовать овладению умения обследовать геометрические.

Конспект занятия с использованием дидактической игры «Поможем Маше и Мишке выучить основные цвета и геометрические фигуры» Мультимедийная игра «Поможем Маше и Мишке выучить основные цвета и геометрические фигуры» Автор: Белашова Татьяна Анатольевна МДАНОУ детский.

Конспект НОД по ФЭМП в подготовительной к школе группе «Как помочь Буратино» Программное содержание: 1. Закрепить знание детей о последовательности дней недели, о временах года, осенних месяцах; 2. Продолжать учить.

Источник

Что такое объемные фигуры

Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту

В этом уроке познакомимся с понятием «объемные тела», а также изучим элементы объемных тел.

Треугольники, квадраты, ромбы, круги, окружности, кубы. Если посмотреть вокруг, то в привычных нам предметах и вещах можно увидеть геометрические фигуры и тела.

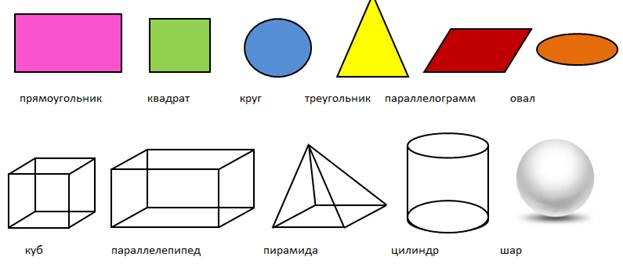
Рассмотрим геометрические фигуры, изображенные на рисунке, и попробуем назвать их.

Фигуры в верхнем ряду нам знакомы, и назвать их не составит труда: прямоугольник, квадрат, круг, треугольник, параллелограмм, овал. Все эти фигуры плоские.

Посмотрим внимательно на фигуры нижнего ряда, там расположены следующие фигуры: куб, параллелепипед, пирамида, цилиндр, шар. Все эти фигуры объемные.

С объемными фигурами мы часто сталкиваемся в обычной жизни.

На какие объемные геометрические фигуры похожи разные предметы?

Автобус формой похож на параллелепипед;

Мячик имеет форму шара;

Банка сгущенки – это цилиндр;

Египетская пирамида – пирамида;

Детские кубики – куб.

Интересно, а в чем отличие объемных геометрических фигур от плоских?

Чтобы ответить на этот вопрос, рассмотрим следующие пары: квадрат и куб, треугольник и пирамида.

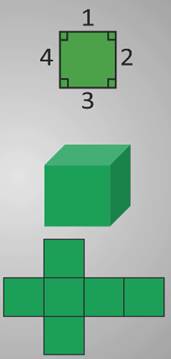
Рассмотрим первую пару: квадрат и куб.

Квадрат – это плоская геометрическая фигура, у которой 4 одинаковые стороны и 4 угла. У квадрата мы можем измерить длину и ширину.

Куб – это объемная фигура.

Если мы развернем куб, то увидим, что он состоит из 6 квадратов.

Значит, квадрат – это элемент куба, его сторона.

У куба мы можем измерить не только длину и ширину, но и высоту.

Рассмотрим вторую пару: треугольник и пирамида.

Треугольник – это плоская геометрическая фигура, у которой 3 стороны и 3 угла.

У треугольника мы можем измерить длины его сторон.

Пирамида – это объемная геометрическая фигура.

Если мы развернем пирамиду, то увидим, что она состоит из 4 треугольников и одного квадрата.

Значит, треугольники и квадрат – это элементы пирамиды, треугольники – это стороны пирамиды, а квадрат – ее основание.

У пирамиды мы можем измерить длину, ширину и высоту.

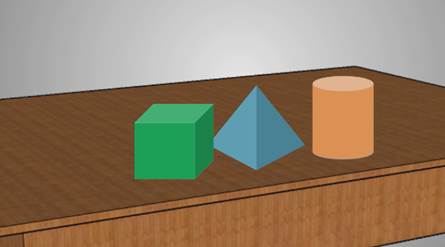
На стол поставим объемные фигуры: куб, пирамиду и цилиндр.

С левой стороны включим настольную лампу.

Объемные фигуры отбрасывают тень.

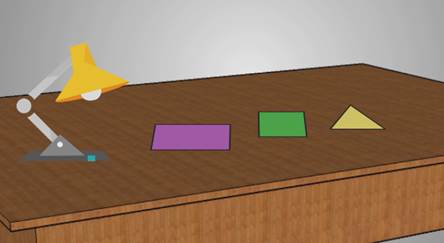
А теперь на стол положим плоские фигуры: квадрат, прямоугольник и треугольник. Включим лампу.

Что заметим на этот раз?

Плоские фигуры не отбрасывают тень, они полностью соприкасаются с поверхностью стола.

Сравнив пары фигур и проведя эксперимент, можем сделать вывод: объемные фигуры отбрасывают тень; у объемных фигур в отличие от плоских имеется три меры: длина, ширина и высота; плоские фигуры являются элементами объемных фигур.

Подведем итоги урока:

1.Все геометрические фигуры в математике можно разделить на две группы: плоские и объемные.

2.Объемные геометрические фигуры – это фигуры, у которых можно измерить длину, ширину и высоту.

3.Объемные фигуры на свету отбрасывают тень.

4.Плоские фигуры являются элементами объемных фигур.

Источник

Объемы геометрических тел

Объемы геометрических тел

Раньше для определения объемов геометрических тел традиционно использовались интегралы. Сегодня есть и другие подходы, которые подробно представлены в учебниках нашей корпорации. В одном из вебинаров «Российского учебника» учитель высшей категории Алексей Доронин рассказал о методах определения объема разных геометрических тел с помощью принципа Кавальери и других аксиом.

Определение объема

Объем можно определить как функцию V на множестве многогранников, удовлетворяющую следующим аксиомам:

Принцип Кавальери (итальянского математика, ученика Галилея). Если при пересечении двух тел плоскостями, параллельными одной и той же плоскости, в сечениях этих тел любой из плоскостей получаются фигуры, площади которых относятся как m : n, то объемы данных тел относятся как m : n.

В открытом банке заданий ЕГЭ есть много задач для отработки этого способа определения объема.

Примеры

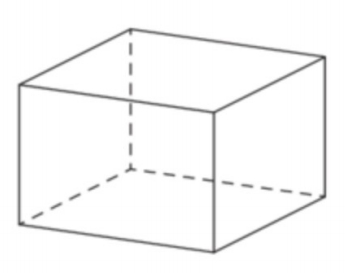
Задача 1. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.

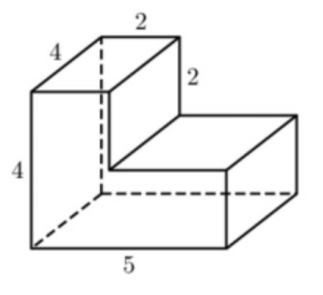
Задача 2. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

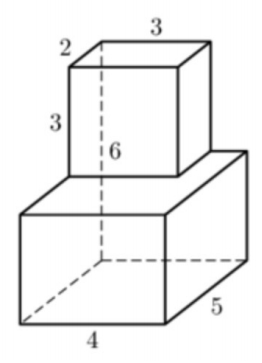
Задача 3. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Разберем, как можно вычислять объемы изучаемых в школе фигур.

Объем призмы

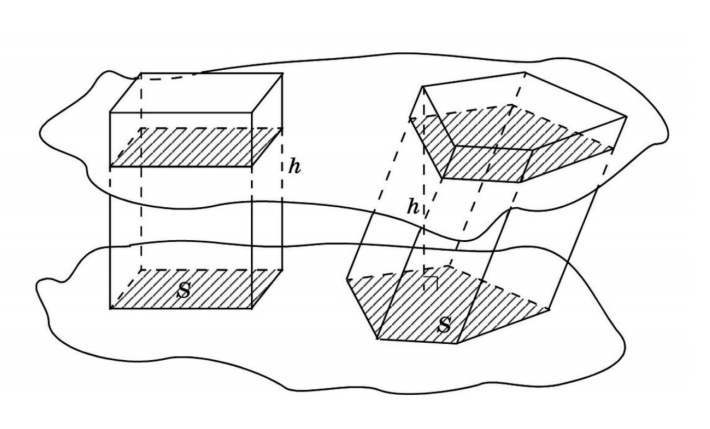
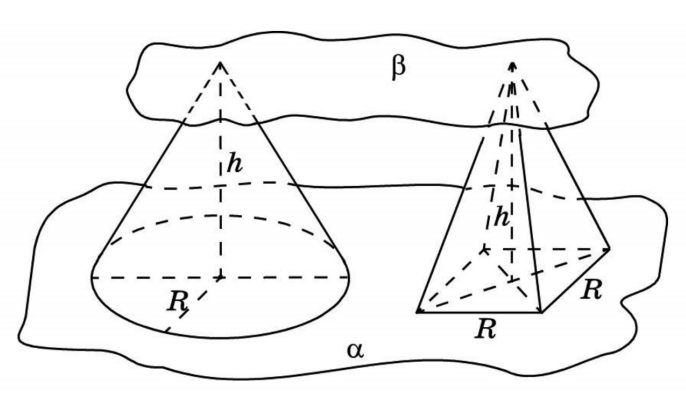
В представленном случае известны площадь основания и высота призмы. Чтобы найти объем, используем принцип Кавальери. Рядом с призмой (Ф₂) поместим прямоугольный параллелепипед (Ф₁), в основании которого — прямоугольник с такой же площадью, как у основания призмы. Высота у параллелепипеда такая же, как у наклонного ребра призмы. Обозначим третью плоскость (α) и рассмотрим сечение. В сечении виден прямоугольник с площадью S и, во втором случае, многоугольник тоже с площадью S. Далее вычисляем по формуле:

Объем пирамиды

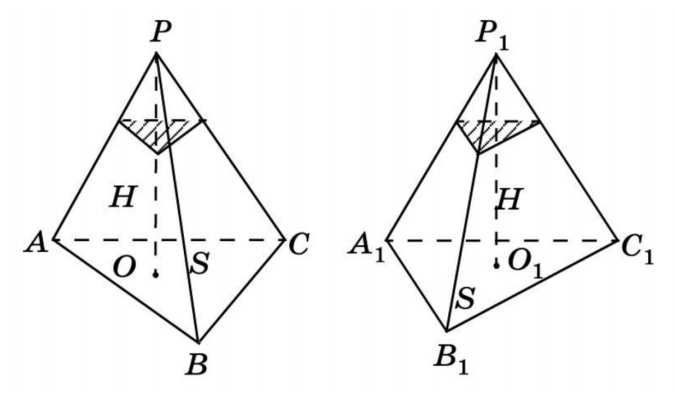
Лемма: две треугольные пирамиды с равновеликими основаниями и равными высотами равновелики. Докажем это, используя принцип Кавальери.

Возьмем две пирамиды одинаковой высоты и заключим их между двумя параллельными плоскостями α и β. Обозначим также секущую плоскость и треугольники в сечениях. Заметим, что отношения площадей этих треугольников связаны непосредственно с отношением оснований.

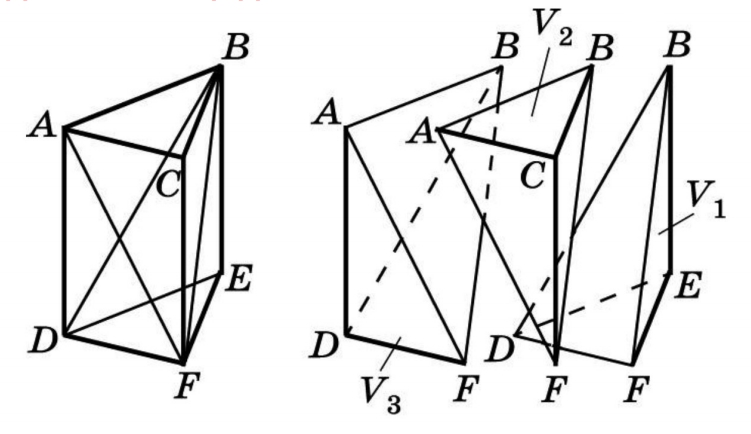
Известно, что объем любой пирамиды равен одной трети произведения площади основания на высоту. Данной теоремой апеллируют довольно часто. Однако откуда в формуле объема пирамиды появляется коэффициент 1/3? Чтобы понять это, возьмем призму и разобьем ее на 3 треугольные пирамиды:

Объем цилиндра

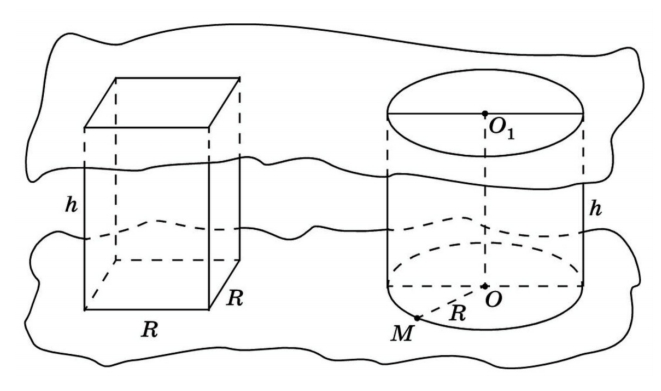
Возьмем прямой круговой цилиндр, в котором известны радиус основания и высота. Рядом поместим прямоугольный параллелепипед, в основании которого лежит квадрат. Рассмотрим:

Объем конуса

Конус лучше всего сравнивать с пирамидой. Например, с правильной четырехугольной пирамидой с квадратом в основании. Две фигуры с равными высотами заключаем в две параллельные плоскости. Обозначив третью плоскость, в сечении получаем круг и квадрат. Представления о подобиях приводят к числу π.

Объем шара

Объем шара — одна из наиболее сложных тем. Если предыдущие фигуры можно продуктивно разобрать за один урок, то шар лучше отложить на последующее занятие.

Итак, чтобы найти объем нового, не изученного геометрического тела, нужно сравнить его с тем телом, которое наиболее на него похоже. Многочисленные примеры заданий из открытого банка задач показывают, что в работе с фигурами имеет смысл использовать представленные формулы и аксиомы.

Источник

Основные геометрические фигуры

Основные понятия

Основные геометрические фигуры на плоскости — это точка и прямая линия. А простейшие фигуры — это луч, отрезок и ломаная линия.

Минимальный объект в геометрии — точка. Ее особенность в том, что она не имеет размеров: у нее нет высоты, длины, радиуса. У точки можно определить только ее расположение, которое принято обозначать одной заглавной буквой латинского алфавита.

Из множества точек может получится линия, а из нескольких соединенных между собой линий — геометрические фигуры.

Обучение на курсах по математике поможет быстрее разобраться в видах и свойствах геометрических фигур.

Каждая математическая фигура имеет собственную величину, которую можно измерить при помощи формул и внимательности.

Площадь — это одна из характеристик замкнутой геометрической фигуры, которая дает нам информацию о ее размере. S (square) — знак площади.

Периметром принято называть сумму длин всех сторон многоугольника. Периметр обозначается заглавной латинской P.

Если параметры переданы в разных единицах измерения длины, нужно перевести все данные к одной единице измерения.

Популярные единицы измерения площади:

Геометрические тела — часть пространства, которая ограничена замкнутой поверхностью своей наружной границы.

Если все точки фигуры принадлежат одной плоскости, значит она является плоской.

Объемная фигура — геометрическая фигура, у которой все точки не находятся на одной плоскости.

Примеры объемных геометрических фигур:

Рассмотрим подробнее некоторые фигуры, разберем их определения и свойства.

Прямоугольник

Прямоугольник — параллелограмм, у которого все углы прямые.

Узнать площадь прямоугольника помогут следующие формулы:

Диагональ — это отрезок, который соединяет противоположные вершины фигуры. Он есть во всех фигурах, число вершин которых больше трех.

Периметр прямоугольника — сумма длины и ширины, умноженная на два.

P = 2 × (a + b), где a — ширина, b — высота.

Квадрат

Квадрат — это тот же прямоугольник, у которого все стороны равны.

Найти площадь квадрата легко:

Периметр квадрата — это длина стороны, умноженная на четыре.

P = 4 × a, где a — длина стороны.

Трапеция

Трапеция — это четырехугольник, у которого две стороны параллельны, а две не параллельны.

Основное свойство: в трапецию можно вписать окружность, если сумма ее оснований равна сумме боковых сторон.

Как найти площадь трапеции:

S = (a + b) : 2 × h, где a, b — два разных основания, h — высота трапеции.

Построить высоту трапеции можно, начертив отрезок так, чтобы он соединил параллельные стороны и был расположен перпендикулярно к этим основаниям.

Формула периметра для равнобедренной трапеции отличается от прямоугольника тем, что у равнобедренной трапеции есть две равные стороны.

P = a + b + 2 × c, где a, b — параллельные стороны, c — две длины одинаковых сторон.

Параллелограмм и ромб

Параллелограмм — четырехугольник, противоположные стороны которого попарно параллельны

Ромб — это параллелограмм с равными сторонами.

Общие формулы расчета площади фигур:

Периметр ромба — это произведение длины стороны на четыре.

P = 4 × a, где a — длина стороны.

Периметр параллелограмма — сумма длины и ширины, умноженная на два.

P = 2 × (a + b), где a — ширина, b — высота.

Треугольник

Треугольник — это такая фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки принято называть вершинами, а отрезки — сторонами.

Рассчитать площадь треугольника можно несколькими способами по исходным данным, давайте их рассмотрим.

S = 0,5 × a × h, где a — длина основания, h — высота, проведенная к основанию.

Основание может быть расположено иначе, например так:

При тупом угле высоту можно отразить на продолжение основания:

При прямом угле основанием и высотой будут его катеты:

S = 0,5 × a × b × sinα, где a и b — две стороны, sinα — синус угла между ними.

S = (a × b × с) : 4 × R, где a, b и с — стороны треугольника, а R — радиус описанной окружности.

S = p × r, где р — полупериметр треугольника, r — радиус вписанной окружности.

Периметр треугольника — это сумма длин трех его сторон.

P = a + b + c, где a, b, c — длина стороны.

Формула измерения периметра для равностороннего треугольника — это длины стороны, умноженная на три.

P = 3 × a, где a — длина стороны.

Круг — это это часть плоскости, которая лежит внутри окружности.

Окружность — это граница круга.

Радиус окружности — это расстояние от центра окружности до любой точки на ней.

Диаметр круга — это отрезок, который соединяет две точки на окружности и проходящий через ее центр. Диаметр круга равен двум его радиусам.

Формулы площади круга:

Периметр круга или длина окружности — это произведение радиуса на два Пи или произведение диаметра на Пи.

L = d × π = 2 × r × π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Источник