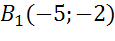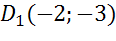Что такое отображение плоскости на себя

Понятие движения

Вы будете перенаправлены на Автор24

Отображение плоскости на себя

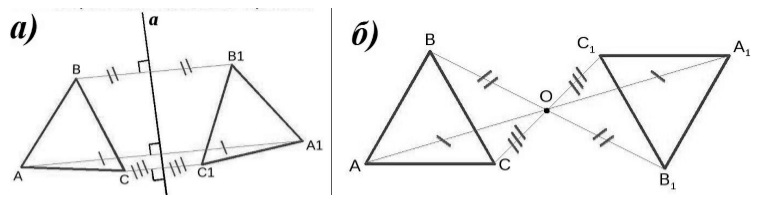
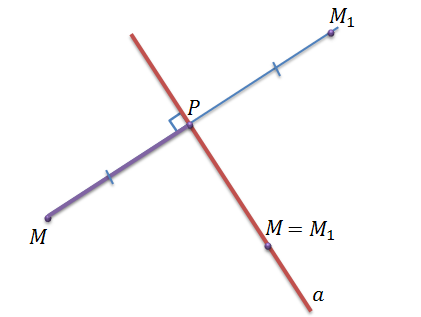
Примерами отображения плоскости на себя могут являться осевая симметрия (рис. 1,а) и центральная симметрия (рис. 1,б).

Рисунок 1. а) осевая симметрия; б) центральная симметрия

Понятие движения

Введем теперь определение движения.

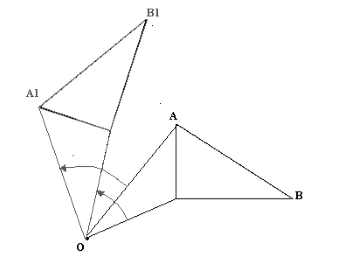
Движением плоскости называется такое отображение плоскости на себя, при котором сохраняются расстояния (рис. 2).

Рисунок 2. Пример движения

Теоремы, связанные с понятием движения

При движении отрезок отображается на равный ему отрезок.

Доказательство.

Рисунок 3. Отображение отрезка на отрезок при движении

Готовые работы на аналогичную тему

Так как, по определению движения, расстояния сохраняются, то

Теорема доказана.

При движении треугольник отображается на равный треугольник.

Доказательство.

Теорема доказана.

Аналогично можно доказать, что луч отображается на луч, угол отображается на равный ему угол.

Для формулирования следующей теоремы вначале ведем следующее определение.

Наложением называется такое движение плоскости, которое обладает следующими аксиомами:

Любое движение является наложением.

Доказательство.

Теорема доказана.

Пример задачи на понятие движения

Доказать, что при движении угол отображается на равный ему угол.

Доказательство.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 15 04 2021

Источник

Геометрия

А Вы уже инвестируете?
Слышали про акцию в подарок?

Зарегистрируйся по этой ссылке
и получи акцию до 100.000 руб

План урока:

Отображение плоскости на себя

Пусть есть некоторое правило, которое устанавливает для каждой точки плоскости какую-нибудь точку этой же плоскости. Подобное правило именуют отображением плоскости на себя.

Лучше всего пояснить это понятие на конкретных примерах. Так, уже изученная нами ранее осевая симметрия может считаться отображением плоскости на себя. Проведем на плоскости прямую m, которая сыграет роль оси симметрии. Далее отметим несколько произвольно выбранных точек А, В, С, D:

Для каждой из отмеченных точек несложно определить точку, симметричную ей относительно оси симметрии. Чтобы сделать это, надо опустить из точек перпендикуляры АА’, ВВ’, СС’на прямую m, а потом на продолжении этих перпендикуляров отложить отрезки А’A’’, B’B’’, C’C’’ так, чтобы выполнялись равенства:

Тогда точки А и А’’, В и В’’, С и С’’ будут симметричны относительно m. Можно сказать, что точки А, В и С отобразились соответственно в точки А’’, В’’, С’’:

Обратите внимание на точку D, которая непосредственно лежит на m. Для нее не получится выполнить такое же построение, как для А, В и C, однако считается, что она симметрична сама себе. Поэтому можно сказать, что точка D преобразуется в точку D’’, которая совпадает с самой D. То есть точка отобразилась сама на себя.

Таким образом, любую точку можно отобразить симметрично относительно произвольной прямой m, и такое отображение как раз является примером отображения плоскости на себя.

В качестве ещё одного примера можно привести центральную симметрию. Отметим на плоскости произвольную точку О, которая будет центром симметрии, а также некоторые точки А, В, С. Отобразим их симметрично относительно О. Для этого надо просто построить прямые АО, ВО и СО, а потом от О отложить на этих прямых отрезки А’О, В’O, C’O:

Можно сказать, что А, В и С отобразились в точки А’, В’ и C’. Если бы мы захотели отобразить с помощью центральной симметрии саму точку О, то она отобразилась бы сама в себя. Таким образом, центральная симметрия также представляет собой отображение плоскости на себя, так как с помощью описанного алгоритма можно найти отображение любой точки на плоскости.

Важно понимать, что бывают отображения плоскости, которые вовсе не являются симметриями. Например, снова возьмем точку О ещё три точки А, В, С. Снова построим прямые АО, ВО и СО, но теперь уже от самих точек А, В и С отложим отрезки, равные АО, ВО и СО, и обозначим их как АА’, ВВ’ и CС’:

В результате наших действий мы снова каждой точке А, В, С поставили в соответствие точку А’, В’, С’. То есть имеет место отображение плоскости. Такое преобразование называется гомотетией (точнее говоря, это частный случай гомотетии), и оно симметрией не является.

Все три описанных примера отображений плоскости на себя объединяет то, что они содержат описание правила (алгоритма), по которому произвольной точке А может быть поставлена в соответствие какая-то произвольная точка А’. При этом точку А’ называют отображением, или образом точки А. В свою очередь А можно назвать прообразом точки А’. Ещё раз отметим, что допускается ситуация, когда точки А и А’ совпадают. Попробуйте сами придумать ещё несколько алгоритмов, которые представляют собой отображения плоскости.

Понятие движения в геометрии

Среди всех отображений плоскости в особую группу объединяют те преобразования, при которых не изменяется расстояние между отображаемыми точками. Эти отображения именуются движениями. Также используются термины перемещение и изометрия.

Центральная и осевая симметрия– это как раз примеры движений. Докажем это для осевой симметрии. Рассмотрим две точки А и В, расположенные так, как это показано на рисунке, а также ось симметрии m. Отобразим А и В относительно mпо правилам осевой симметрии:

Здесь Н и К – это точки прямой m, на которые упали перпендикуляры, опущенные из А и В. Проведем отрезки НВ и НВ’. Теперь исследуем ∆KBH и ∆KB’H. Они оба являются прямоугольными, у них один катет общий (HK), а вторые катеты равны по свойству осевой симметрии. Из этого вытекает равенство ∆KBH и ∆KB’H, а это значит, что

Далее рассмотрим ∆АВН и ∆А’B’H. Только что мы выяснили, что у них есть одинаковые углы ∠BHA и ∠B’HA’. Прилегающие к ним стороны также одинаковы:

Надо отметить, что приведенное доказательство не является полным, так как рассматривает один случай расположения точек А и В. Возможны ещё как минимум 6 случаев расположения А и В:

В рамках полного доказательства следовало бы полностью рассмотреть каждый из этих случаев и для каждого из них доказать равенство

но мы не будем тратить на это время, можете попробовать самостоятельно сделать это.

Далее проанализируем центральную симметрию, она также представляет собой движения. Отобразим точки А и В в образы А’и В’ относительного произвольного центра симметрии О:

Сравним ∆АОВ и А’OB’. У них одинаковы∠АОВ и ∠А’ОВ’, так как они – вертикальные. По свойству центральной симметрии можно записать, что

Надо понимать, что не всякое отображение плоскости представляет собой движение. Например, рассмотренная нами гомотетия изменяет расстояния между точками, а потому она не относится к движениям.

Свойства движения

При движении, как и при любом отображении, можно отображать не только отдельные точки, но и их множества, то есть геометрические фигуры. Сформулируем важную теорему:

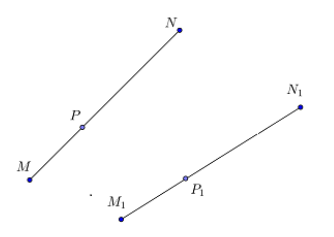
Действительно, пусть есть отрезок MN, все точки которого мы отобразили с помощью движения. Произвольную точку отрезка MN обозначим как Р. После отображения мы получим точки M’, N’ и Р’. Соединим М’ и N’ и получим отрезок M’N’.Докажем, что Р’ принадлежать отрезку M’N’.

Р лежит на NP, поэтому справедливо равенство:

Заметим, что это равенство как раз может выполняться только в случае, если Р’ принадлежит M’N’. Действительно, если Р’ не лежит на M’N’, то существует ∆M’N’P’, для которого, в силу неравенства треугольника, можно записать

Итак, мы показали, что всякая точка Р исходного отрезка MN обязательно будет отображаться на отрезок M’N’. Однако этого мало. Вдруг на M’N’ есть такая точка Р’, что ее прообраз не лежит на исходном отрезке MN?Для того, чтобы опровергнуть такую возможность, надо рассуждать в «обратную сторону». Для Р’, лежащей на M’N’, выполняется равенство

Такое равенство означает, что Р лежит на MN. В итоге мы смогли показать, что отрезок MN отображается именно в отрезок M’N’.

Доказанное нами свойство позволяет доказать следующий факт:

В результате отрезки АВ, АС, и ВС отобразятся в равные им отрезки А’B’, А’С’ и B’C’. Но тогда ∆АВС и ∆А’В’С’ будут равны, ведь у них одинаковы все 3 стороны, ч. т. д.

Из этого факта легко показать, что при движении остаются неизменными не только расстояния, но и углы. Пусть есть некоторый ∠А. Отметим на его сторонах точки В и C, в результате получим ∆АВС (если только ∠А не является развернутым). При движении ∆АВС отобразится в равный ему ∆А’В’С’. Из равенства треугольников вытекает и равенство углов:

Аналогичными рассуждениями можно продемонстрировать, что вообще любая фигура, изученная нами в курсе геометрии (прямая, луч, многоугольник, окружность) будет отображаться в равную ей фигуру.

Более того, если между двумя фигурами есть некоторая взаимосвязь, то она сохраняется после движения. Например, при движении две параллельные прямые отображаются в две другие параллельные прямые, и расстояние между ними не меняется. Если движению подвергают окружность и прямую, являющуюся касательной к ней, то в результате получают новую окружность и прямую, причем прямая останется касательной к окружности.

Параллельный перенос

Мы уже изучили два вида движения – осевую и центральную симметрию. Однако есть ещё несколько видов движений. Один из них именуется параллельным переносом. Для выполнения параллельного переноса необходимо предварительно задать некоторый вектор а. При параллельном переносе точки М она отображается в точку M’ так, что вектор MM’ оказывается равным а. Переносить можно сразу множество точек.

Докажем, что параллельный перенос действительно представляет собой движение. Для этого надо всего лишь продемонстрировать, что при нем расстояние между двумя произвольными точками не меняется. Пусть в результате параллельного переноса на вектор а некоторые точки M и N отобразились в M’ и N’ соответственно:

Рассмотрим получившийся четырехугольник NMM’N’. Две его стороны, MM’ и NN’, параллельны и имеют одинаковую длину, так являются равными векторами. Это значит, что NMM’N’ – это параллелограмм (согласно одному из признаков параллелограмма). Но тогда и две другие стороны NMM’N’, то есть MN и M’N’, также одинаковы, ч. т. д.

Примечание. Возможен частный случай, когда отрезок MN параллелен вектору а. В этом частном случае построить параллелограмм не удастся, но вы можете убедиться самостоятельно, что и в этом случае расстояние между M и N не изменяется.

Параллельный перенос может быть использован при решении ряда задач, в том числе и связанных с построением.

Задание. Даны две непересекающиеся окружности с различными радиусами. Постройте общие внешние касательные к этим окружностям.

Решение. Предположим, что нам удалось построить обе внешние касательные. Обозначим точки касания как К, Р, M и N:

Теперь осуществим параллельный перенос касательных. Касательную КР перенесем на вектор КО₁, а MN – на вектор MО₁. В результате точки K и M отобразятся в О₁, а точки Р и N – в точки Р’ и N’:

Так как при движении углы сохраняются, то прямые О₁Р’ и О₂N’ останутся перпендикулярными радиусам О₂Р и О₂N. Значит, если построить окружность с радиусом О₂Р’ (а его величина равна R – r), то для нее эти прямые останутся касательными. Отсюда легко понять алгоритм построения внешних касательных. Сначала надо построить отрезок длиной R– r (на рисунке показан зеленым цветом):

Далее из О₂ проводим окружность с радиусом R– r:

Теперь из точки О₁ проводим касательные к новой окружности. Построение таких касательных – отдельная геометрическая задача, изучаемая ещё в 8 классе. В результате мы сможем найти точки касания Р’ и N’:

Далее надо найти осуществить параллельный перенос касательных. Для этого продолжаем радиусы О₂Р’ и О₂N’, пока они не пересекутся с большей окружностью в точках Р и N соответственно. Чтобы найти точки касания меньшей окружности, надо просто провести перпендикуляры к касательным:

Поворот

Ещё одно движение, используемое в планиметрии – это поворот. Для того, чтобы его совершить, необходимо указать центр поворота и выбрать угол поворота, а также задать направление вращение. На следующем рисунке показан поворот точки М относительно О на угол 45° по часовой стрелке:

В общем случае поворот относительно точки О на некоторый угол α– это такое отображение, при котором произвольная точка М преобразуется в М’, и при этом выполняется два равенства:

Поворачивать можно не только точки, но и целые фигуры. Например, ниже продемонстрирован поворот треугольника:

Докажем, что поворот действительно является движением, то есть при его применении расстояния не искажаются. Пусть точки M и N поворачиваются на угол α относительно точки О:

Тогда по определению поворота можно записать:

Использование движения в задачах

Мы уже рассмотрели одну задачу на построение, в которой применялся параллельный перенос прямой. Однако чаще в задачах используется поворот, а также различные виды симметрии.

Задание. Точки А и В лежат по одну сторону от прямой m. Как, используя только циркуль и линейку, отметить на m такую точку C, что сумма длин отрезков АС и ВС будет минимально возможной?

Решение. Отобразим А симметрично относительно прямой m и получим точку А’. После этого соединим А’ с В. Отрезок пересечет m в точке, которая как раз и будет искомой точкой С:

Действительно, по свойству движения отрезки АС и А’С одинаковы, поэтому сумма длин АС и ВС будет совпадать с суммой А’С и ВС, то есть будет равна длине А’В. Если бы выбрали вместо С какую-нибудь другую точку К, не лежащую на А’В, то сумма длин А’K и ВК оказалась бы больше, чем длина А’В вследствие неравенства треугольника, записанного для ∆А’KB.

Задание. Петя и Ваня играют в игру. Они по очереди кладут одинаковые круглые фишки на прямоугольный стол. До тех пор, пока это возможно сделать. Если игрок не может сделать ход, то он проигрывает. Какова оптимальная стратегия в этой игре и кто, используя ее, выиграет игру?

Решение. Заметим, что прямоугольный стол обладает центральной симметрией относительно своего центра (центр прямоугольника можно определить как точку, в которой пересекаются его диагонали). Пусть первый игрок положит первую фишку ровно в центр стола:

Далее на любой второго игрока первый игрок может положить свою фишку симметрично относительно центра стола (число в центре круга – номер хода):

Получается, что на ход второго игрока первый всегда сможет ответить. То есть первый игрок никак не может проиграть, используя эту тактику. Так как игра когда-нибудь окончится (ведь свободная площадь на столе рано или поздно закончится), и она не может завершиться вничью, то именно первый игрок и выиграет.

Задание. Для произвольного ∆АВС отмечены точки А₁, В₁ и С₁ так, что ∆А₁ВС, ∆АВ₁С и ∆АВС₁ являются равносторонними, причем никакие из этих четырех треугольников не имеют общей площади (в таких случаях говорят, что треугольники построены внешним образом). Докажите, что отрезки АА₁, ВВ₁ и СС₁ имеют одинаковую длину.

Решение. Напомним, что в равносторонних треугольниках все углы составляют по 60°. Выберем любую из вершин ∆АВС (например, С) и повернем отрезок АА₁ на 60° против часовой стрелки. Тогда точка А₁ отобразится в В, а точка А – в точку В₁.

В итоге отрезок АА₁ отобразился в отрезок ВВ₁. Это значит, что они одинаковы. Аналогичным образом, осуществляя поворот вокруг вершины А, можно показать, что отрезок ВВ₁ переходит в отрезок СС₁, и потому они также одинаковы. Таким образом, все три отрезка имеют одну и ту же длину.

Задание. В ∆АВС проведена медиана СМ. На стороне АС внешним образом построен квадрат АСDE, а на стороне ВС – квадрат ВСKF (также внешним образом). Докажите, что СМ вдвое короче KD, и СМ перпендикулярен KD.

Решение. Повернем ∆АВС на 90° против часовой стрелки вокруг точки С вместе с медианой СМ. Тогда точка А перейдет в точку D, а М и B отобразятся в некоторые точки M’ и B’ соответственно:

Заметим, что ∠ВСК – прямой, так как это угол квадрата. ∠ВСВ’ также прямой, ведь поворот мы осуществили как раз на 90°. Тогда ∠В’СКокажется развернутым:

Это значит, что точки В’, С и К лежат на одной прямой. Отрезки ВС и СК одинаковы как стороны квадрата, а отрезок В’С имеет ту же длину, что и ВС (так как он получен поворотом ВС, а при повороте расстояния не искажаются). Тогда можно записать, что

то есть отрезки СК и В’C также одинаковы. Это означает, что С – середина В’К.

М – это середина АВ (по определению медианы), поэтому и при повороте М’ останется серединой В’D. Получается, что отрезок СМ’ соединяет середины сторон В’К и В’D в ∆В’KD, то есть отрезок СМ’ является средней линией. Отсюда сразу вытекает два факта:

1) М’C вдвое короче КD;

2) М’C параллелен KD.

Ясно, что отрезки МС и М’C одинаковы по определению движения, поэтому МС также будет в 2 раза короче KD:

Отрезки МС и М’C перпендикулярны, ведь поворот мы выполнили на 90°. Но тогда МС также будет перпендикулярен и КD, ведь KD и М’C параллельны, ч. т. д.

Сегодня мы познакомились с понятием отображения плоскости на себя и его частным случаем – движением. При движении сохраняются все расстояния между точками, все углы, формы фигур и все соотношения между геометрическими объектами. Это свойство движения позволяет находить краткие решения весьма сложных геометрических задач.

Источник

Отображение плоскости на себя

Урок 39. Геометрия 9 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Отображение плоскости на себя»

Если каждой точке плоскости ставится в соответствие какая-то точка этой же плоскости, причем любая точка плоскости оказывается сопоставленной некоторой точке, то говорят, что дано отображение плоскости на себя.

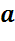
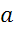
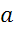
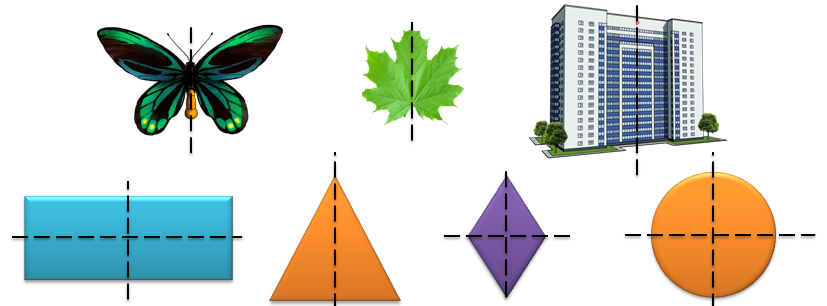
Мы уже встречались с примерами отображения плоскости на себя. Это осевая симметрия. Фигура называется симметричной относительно прямой , если для каждой точки фигуры симметричная ей точка относительно прямой также принадлежит этой фигуре. Прямая называется осью симметрии фигуры. Про такую фигуру говорят, что она обладает осевой симметрией.

Давайте приведем примеры таких фигур из жизни и геометрии. Например, бабочка обладает осью симметрии. У бабочки крылья симметричны относительно брюшка, кленовый лист симметричен относительно одной из центральных жилок. Вообще в нашей жизни очень много примеров осевой симметрии. В геометрии к фигурам с осевой симметрией относятся: прямоугольник, равнобедренный треугольник, ромб и другие.

То что осевая симметрия является примером отображения плоскости на себя доказать нетрудно.

Пусть a – это ось симметрии. Возьмем произвольную точку М, которая не лежит на прямой a и построим симметричную ей точку М один относительно прямой a. Для этого нужно провести перпендикуляр MP к прямой a и отложить на этом перпендикуляре отрезок PM₁=MP. Точка М₁ – искомая.

Если точка М лежит на прямой a, то симметричная ей точка М один совпадает с точкой М. То есть каждой точке М плоскости ставиться в соответствие точка M₁ этой плоскости. Этот факт доказывает, то что осевая симметрия является примером отображения плоскости на себя.

Вспомним еще один вид симметрии – центральную симметрию.

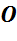
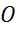
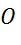
Фигура называется симметричной относительно точки , если для каждой точки фигуры симметричная ей точка относительно точки также принадлежит этой фигуре. Точка называется центром симметрии фигуры.

Примерами центрально симметричных фигур можно назвать некоторые цветы. В геометрии яркими примерами центрально симметричных фигур являются окружность (центр симметрии – центр окружности) и параллелограмм (центром симметрии является точка пересечения диагоналей).

Доказать то, что центральная симметрия является примером отображения плоскости на себя, нетрудно. Пусть точка О – центр симметрии. Возьмем произвольную точку М и построим точку, которая симметрична точке М относительно центра симметрии О. Для этого соединим точки М и О и на продолжении прямой МО отложим отрезок О М₁ равный отрезку МО. Точка М₁ – искомая точка.

То есть мы доказали, что центральная симметрия тоже является примером отображения плоскости на себя.

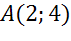
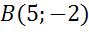
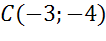
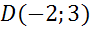
Задача. Пусть в координатной плоскости имеются точки , , , . Построить точки симметричные:

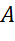
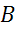
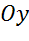
а) точкам и относительно оси ;

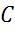
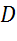
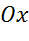
б) точкам и относительно оси ;

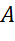
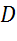
в) точкам и относительно начала координат.

а) ;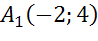

б) ;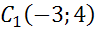

в) ;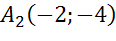

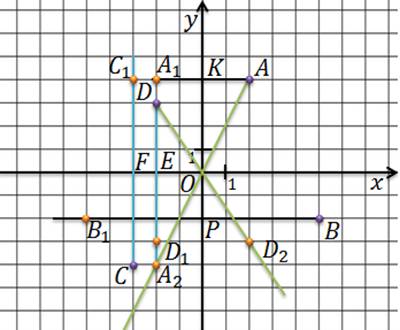
Для того, чтобы построить точки, симметричные точкам А и B относительно оси Оy, необходимо из точек А и B провести перпендикуляр к оси Оy и затем на продолжении этих перпендикуляров отложить отрезки равные АК и BP соответственно. Тогда получим точки A_1, B₁, которые симметричны точкам А и B относительно оси Оy.

Аналогично, для построения точек симметричных точкам C и D относительно оси Ox, опустим из этих точек перпендикуляры на ось Ox и на продолжении перпендикуляров отложим отрезки равные отрезкам CE и DF соответственно. Таким образом, мы получим точки C₁D₁ симметричны точкам C и D относительно оси Ox.

Для того, чтобы построить точки, симметричные точкам А и D относительно начала координат, соединим точки А и D с началом координат и на продолжении этих прямых отложим отрезки, равные АО и DО соответственно. Получим точки A2 и D2. Эти точки и будут симметричными точкам А и D относительно начала координат.

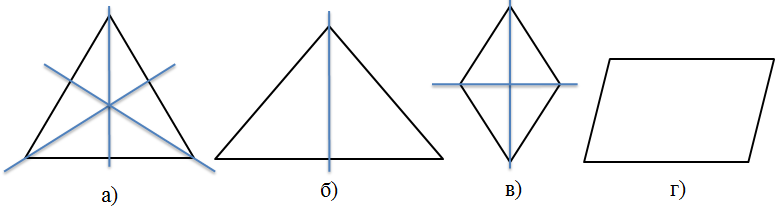
Задача. Указать количество осей симметрии:

a) у равностороннего треугольника 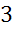оси симметрии;

б) у равнобедренного треугольника 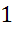ось симметрии;

в) у ромба 2 оси симметрии;

г) у параллелограмма нет осей симметрии.

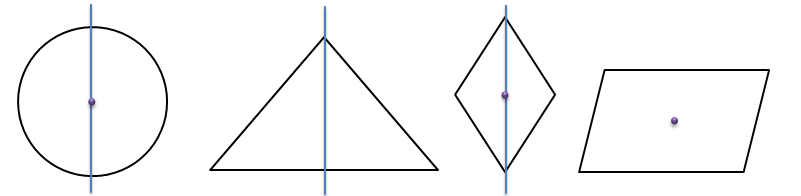
Задача. Среди представленных фигур укажите фигуры, у которых:

а) есть ось симметрии;

б) есть центр симметрии.

Легко увидеть, что ось симметрии имеют все фигуры кроме параллелограмма. А вот центр симметрии будут иметь окружность, ромб и параллелограмм.

Подведем итоги урока. Сегодня мы ввели понятие отображения плоскости на себя. Мы сказали, что если каждой точке плоскости ставится в соответствие какая-то точка этой же плоскости, причем любая точка плоскости оказывается сопоставленной некоторой точке, то говорят, что дано отображение плоскости на себя.

Вспомнили такие понятия как центральная и осевая симметрия.

Источник