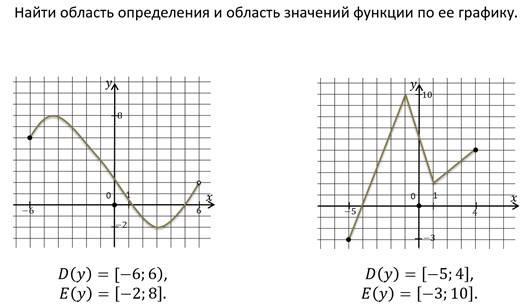
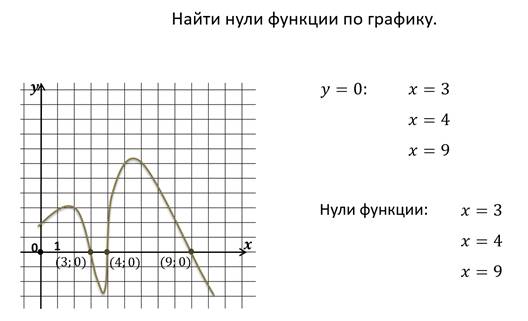
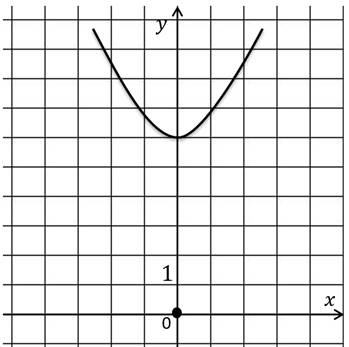
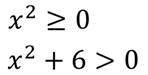Что такое область определения функции и область значения функции простыми словами
Область значений функции (множество значений функции). Необходимые понятия и примеры нахождения
Зачастую в рамках решения задач нам приходится искать множество значений функции на области определения или отрезке. Например, это нужно делать при решении разных типов неравенств, оценках выражений и др.
В рамках этого материала мы расскажем, что из себя представляет область значений функции, приведем основные методы, которыми ее можно вычислить, и разберем задачи различной степени сложности. Для наглядности отдельные положения проиллюстрированы графиками. Прочитав эту статью, вы получите исчерпывающее представление об области значений функции.
Начнем с базовых определений.
Обратите внимание, что понятие множества значений функции не всегда тождественно области ее значений. Эти понятия будут равнозначны только в том случае, если интервал значений x при нахождении множества значений совпадет с областью определения функции.
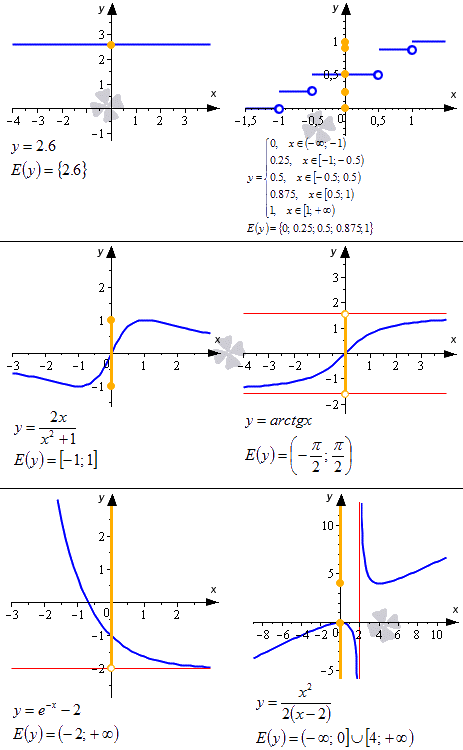
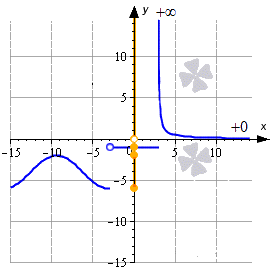
Ниже приводится иллюстрация, на которой показаны некоторые примеры. Синие линии – это графики функций, красные – асимптоты, рыжие точки и линии на оси ординат – это области значений функции.
Рассмотрим основные способы нахождения области значений функции.
Возьмем задачу, в которой нужно определить область значений арксинуса.
Решение
Решение
Все, что нам нужно сделать, – это вычислить наибольшее и наименьшее значение функции в заданном интервале.
Для определения точек экстремума надо произвести следующие вычисления:
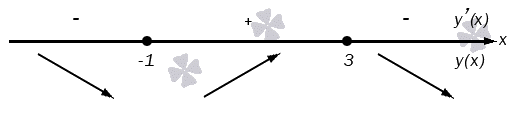
Начнем с определения наибольшей и наименьшей точки, а также промежутков возрастания и убывания на заданном интервале. После этого нам нужно будет вычислить односторонние пределы в концах интервала и/или пределы на бесконечности. Иными словами, нам надо определить поведении функции в заданных условиях. Для этого у нас есть все необходимые данные.
Решение
Определяем наибольшее и наименьшее значение функции на заданном отрезке
Решение
Решение
Мы получили, что значения функции будут возрастать от минус бесконечности до плюс бесконечности при изменении значений x от нуля до плюс бесконечности. Значит, множество всех действительных чисел – это и есть область значений функции натурального логарифма.
Ответ: множество всех действительных чисел – область значений функции натурального логарифма.
Решение
Данная функция является определенной при условии, что x – действительное число. Вычислим наибольшие и наименьшие значения функции, а также промежутки ее возрастания и убывания:
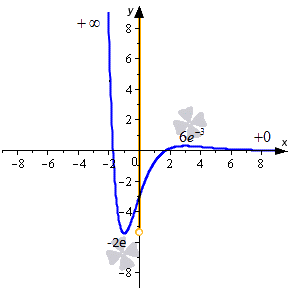
Посмотрим, как же ведет себя функция на бесконечности:
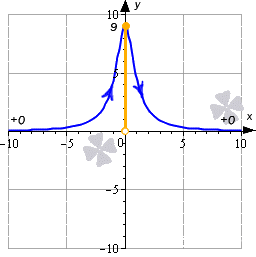
Из записи видно, что значения функции в этом случае будут асимптотически приближаться к 0.
На нем видно, что областью значений функции будет интервал E ( y ) = ( 0 ; 9 ]
Ответ: E ( y ) = ( 0 ; 9 ]
А как быть в случае, если область определения некоторой функции представляет из себя объединение нескольких промежутков? Тогда нам надо вычислить множества значений на каждом из этих промежутков и объединить их.
Решение
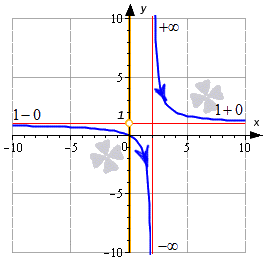
Для открытого луча 2 ; + ∞ производим точно такие же действия. Функция на нем также является убывающей:
Это можно увидеть на графике:
Особый случай – периодические функции. Их область значения совпадает с множеством значений на том промежутке, который отвечает периоду этой функции.
Решение
Синус относится к периодической функции, а его период составляет 2 пи. Берем отрезок 0 ; 2 π и смотрим, каким будет множество значений на нем.
Если вам нужно знать области значений таких функций, как степенная, показательная, логарифмическая, тригонометрическая, обратная тригонометрическая, то советуем вам перечитать статью об основных элементарных функциях. Теория, которую мы приводим здесь, позволяет проверить указанные там значения. Их желательно выучить, поскольку они часто требуются при решении задач. Если вы знаете области значений основных функций, то легко сможете находить области функций, которые получены из элементарных с помощью геометрического преобразования.
Решение
Еще один пример запишем без пояснений, т.к. он полностью аналогичен предыдущему.
Решение
Теперь разберем, как найти область значений функции, которая не является непрерывной. Для этого нам надо разбить всю область на промежутки и найти множества значений на каждом из них, после чего объединить то, что получилось. Чтобы лучше понять это, советуем повторить основные виды точек разрыва функции.
Решение
Решение показано на графике:
Решение
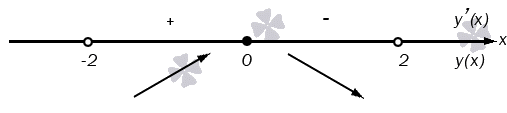
Она определена для всех значений аргумента, представляющих собой действительные числа. Определим, в каких промежутках данная функция будет возрастать, а в каких убывать:
Теперь найдем соответствующие значения функции:
Посмотрим на поведение функции на бесконечности:
Для вычисления второго предела было использовано правило Лопиталя. Изобразим ход нашего решения на графике.
Область определения функции
Прежде чем перейти к изучению области определения функции внимательно изучите уроки
«Что такое функция в математике» и «Как решать задачи на функцию».
Вспомним кратко основные определения функции в математике.
Функция — это зависимость переменной « y » от независимой переменной « x ».
Функцию можно задать через формулу (аналитически). Например:
Вместо « x » (аргумента функции) в формулу « у = 2x » подставляем произвольные числовые значения и по заданной формуле вычисляем
значение « y ».
Подставим несколько числовых значений вместо « x » в формулу « у = 2x » и запишем результаты в таблицу.
| x | y = 2 x | ||||||
|---|---|---|---|---|---|---|---|
| x = −2 | у = 2 · (−2) = −4 | ||||||
| x = 0 | y = 2 · 0 = 0 | ||||||
x =
| y = 2 ·
=
= 1 | ||||||
| x = 3 | y = 2 · 3 = 6 |
Область определения функции — это множество числовых значений, которые можно подставить вместо « x » (аргумента функции).
Обозначают область определения функции как:
Вернемся к нашей функции « у = 2x » и найдем её область определения.
Посмотрим ещё раз на таблицу функции « y = 2x », где мы подставляли произвольные числа вместо « x », чтобы найти « y ».
| x | y = 2x | ||
|---|---|---|---|
| −2 | −4 | ||
| 0 | 0 | ||
| 1 | ||
| 3 | 6 |
Так как у нас не было никаких ограничений на числа, которые можно подставить вместо « x », можно утверждать, что вместо « x » мы могли подставлять любое действительное число.
Другими словами, вместо « x » можно подставить любые числа, например:
В нашей функции « у = 2x » вместо « x » можно подставить любое число, поэтому область определения функции « у = 2x » — это любые действительные числа.
Запишем область определения функции « у = 2x » через математические обозначения.
Ответ выше написан словами без использования специального математического языка. Заменим лишние слова на математические символы. Для этого вспомним понятие числовой оси.
Заштрихуем область на числовой оси, откуда можно брать значения для « x » в функции « у = 2x ». Так как в функции
« у = 2x » нет ограничений для « x », заштрихуем всю числовую ось от минус бесконечности « −∞ » до плюс бесконечности « +∞ ».
Запись выше читается как: « x » принадлежит промежутку от минус бесконечности до плюс бесконечности.
Запишем окончательный ответ для области определения функции.
По-другому промежуток
« x ∈ (−∞ ; +∞) » можно записать
как « x ∈ R ».
Читается « x ∈ R » как: « x » принадлежит всем действительным числам».
Записи « x ∈ (−∞ ; +∞) » и
« x ∈ R » одинаковы по своей сути.
Область определения функции с дробью
Разберем пример сложнее, когда в задании на поиск области определения функции есть дробь с « x » в знаменателе.
№ 233 (2) Мерзляк 8 класс
Найдите область определения функции:
Задание «Найдите область определения функции» означает, что нам нужно определить все числовые значения, которые может принимать « x » в функции
« f(x) =
| 8 |
| x + 5 |
».
По законам математики из школьного курса мы помним, что на ноль делить нельзя. Иначе говоря, знаменатель (нижняя часть дроби) не может быть равен нулю.
Переменная « x » находится в знаменателе функции « f(x) =
| 8 |
| x + 5 |
». Так как на ноль делить нельзя, запишем, что знаменатель не равен нулю.
Получается, что « x » может принимать любые числовые значения кроме « −5 ». На числовой оси заштрихуем все доступные значения для « x ».
Число « −5 » отмечено «пустой» точкой на числовой оси, так как не входит в область допустимых значений.
Запишем заштрихованную область на числовой оси через знаки неравенства.
Запишем промежутки через математические символы. Так как число « −5 » не входит в область определения функции, при записи ответа рядом с ним будет стоять круглая скобка.
Вспомнить запись ответа через математические символы можно в уроке «Как записать ответ неравенства».
Запишем окончательный ответ для области определения функции
« f(x) =
| 8 |
| x + 5 |
».
Область определения функции с корнем
Рассмотрим другой пример. Требуется определить область определения функции, в которой содержится квадратный корень.
№ 98 (5) Колягин (Алимов) 8 класс
Найти область определения функции:
Из урока «Квадратный корень» мы помним, что подкоренное выражение корня чётной степени должно быть больше или равно нулю.
Найдём, какие значения может принимать « x » в функции
« у = √ 6 − x ». Подкоренное выражение
« 6 − x » должно быть больше или равно нулю.
Решим линейное неравенство по правилам урока «Решение линейных неравенств».
Запишем полученный ответ, используя числовую ось и математические символы. Число « 6 » отмечено «заполненной» точкой на числовой оси, так как входит в область допустимых значений.
Правило для определения области определения функции
Чтобы найти область определения функции нужно проверить формулу функции по двум законам школьного курса математики:
При нахождении области определения функции необходимо всегда задавать себе два вопроса:
Если на оба вопроса вы получаете отрицательный ответ, то область определения функции — это все действительные числа.
Рассмотрим пример поиска области определения функции с корнем и дробью.
№ 242 (3) Мерзляк 8 класс
Найдите область определения функции:
Идем по алгоритму. Задаём себе первый вопрос, есть ли в функции дробь с « x » в знаменателе. Ответ: да, есть.
В функции « f(x) = √ x + 3 +
| 1 |
| x 2 − 9 |
» есть дробь «
| 1 |
| x 2 − 9 |
», где « x » расположен в знаменателе. Запишем условие, что знаменатель « x 2 − 9 » не может быть равен нулю.
Решаем квадратное уравнение через формулу квадратного уравнения.
x1;2 =
| −b ± √ b 2 − 4ac |
| 2a |
x1;2 =
| −0 ± √ 0 2 − 4 · 1 · (−9) |
| 2 · 1 |
x1;2 ≠
| −0 ± √ 0 − (−36) |
| 2 |
Запомним полученный результат. Задаем себе второй вопрос. Проверяем, есть ли в формуле функции
« f(x) = √ x + 3 +
| 1 |
| x 2 − 9 |
» корень четной степени. В формуле есть квадратный корень « √ x + 3 ». Подкоренное выражение « x + 3 » должно быть больше или равно нулю.
Решим линейное неравенство.
Объединим полученные ответы по обоим вопросам:
Объединим все полученные результаты на числовых осях. Сравнивая полученные множества, выберем только те промежутки, которые удовлетворяют обоим условиям.
Выделим красным заштрихованные промежутки, которые совпадают на обеих числовых осях. Обратим внимание, что числа « −3 » и « 3 » отмечены «пустыми» точками и не входят в итоговое решение.

промежутка « −3 » и « x > 3 », которые являются областью определения функции
« f(x) = √ x + 3 +
| 1 |
| x 2 − 9 |
». Запишем окончательный ответ.
Примеры определения области определения функции
№ 101 Колягин (Алимов) 8 класс
Найти область определения функции:
Для поиска области определения функций задаем себе первый вопрос. Есть ли знаменатель, в котором содержится « x »?
Ответ: в формуле функции
« y = 6 √ x + 5 √ 1 + x » нет дробей.
Задаем второй вопрос. Есть ли в функции корни четной степени?
Ответ: в функции есть корень шестой степени: « 6 √ x ». Степень корня — число « 6 ». Число « 6 » — чётное, поэтому подкоренное выражение корня « 6 √ x » должно быть больше или равно нулю.
В формуле функции « y = 6 √ x + 5 √ 1 + x » также есть корень пятой степени
« 5 √ 1 + x ». Степень корня « 5 » — нечётное число, значит, никаких ограничений на подкоренное выражение « 1 + x » не накладывается.
Получается, что единственное ограничение области определения функции
« y = 6 √ x + 5 √ 1 + x » — это ограничение подкоренного выражения « 6 √ x ».
Нарисуем область определения функции на числовой оси и запишем ответ.
№ 242 (4) Мерзляк 8 класс
Найдите область определения функции:
Есть ли в функции знаменатель, в котором содержится « x »? В заданной функции подобных знаменателей два. Выделим знаменатели с « x » красным цветом.
Запишем условие, что каждый из знаменателей не должен быть равен нулю.
| √ x + 2 ≠ 0 |
| x 2 − 7x + 6 ≠ 0 |
Обозначим их номерами « 1 » и « 2 » и решим каждое уравнение отдельно.
| √ x + 2 ≠ 0 (1) |
| x 2 − 7x + 6 ≠ 0 (2) |
Решаем первое уравнение.
Если значение квадратного корня
« √ x + 2 ≠ 0 » не должно быть равно нулю, значит, подкоренное выражение
« x + 2 ≠ 0 » также не должно быть равно нулю.
Теперь решим уравнение под номером « 2 », используя формулу квадратного уравнения.
x1;2 =
| −b ± √ b 2 − 4ac |
| 2a |
x1;2 =
| −(−7) ± √ (−7) 2 − 4 · 1 · 6 |
| 2 · 1 |
x1;2 =
| 7 ± √ 49 − 24 |
| 2 |
x1;2 =
| 7 ± 5 |
| 2 |
x1 ≠
| x2 ≠
|
x1 ≠
| x2 ≠
|
| x1 ≠ 6 | x2 ≠ 1 |
Запишем все полученные ответы в порядке возрастания вместе под знаком системы, чтобы их не забыть.
| x ≠ −2 |
| x ≠ 1 |
| x ≠ 6 |
В формуле функции
« f(x) =
| √ x − 4 |
| √ x + 2 |
+
| 4x − 3 |
| x 2 − 7x + 6 |
»
есть два корня « √ x − 4 » и « √ x + 2 ». Их подкоренные выражения должны быть больше или равны нулю.
| x − 4 ≥ 0 |
| x + 2 ≥ 0 |
| x − 4 ≥ 0 |
| x + 2 ≥ 0 |
| x ≥ 4 |
| x ≥ −2 |
Нарисуем полученные решения на числовой оси. Выберем заштрихованный промежуток, который есть на обеих числовых осях.
Выпишем результат решения системы неравенств.
Объединим в таблицу ниже полученные ответы по обеим проверкам:
Результат проверки, что знаменатели дробей с « x » не равны нулю
Результат проверки, что подкоренные выражения должно быть больше или равны нулю
Нарисуем полученные результаты проверок на числовых осях, чтобы определить, какая заштрихованная область удовлетворяет всем полученным условиям.
Понятие функции. Область определения и область значений функции. Свойства функций
Урок 38. Подготовка к ОГЭ по математике 9 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Понятие функции. Область определения и область значений функции. Свойства функций»
· вспомнить основные сведения о координатной плоскости, функции;
· повторить основные свойства функции.
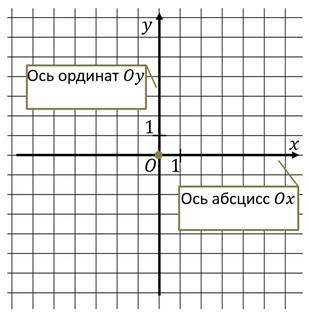
Начнём мы с вами с координатной плоскости.
Таким образом, мы задали на плоскости прямоугольную систему координат.
Плоскость, на которой задана система координат, называют координатной плоскостью.
Повторим определение функции.
Зависимость одной переменной у от переменной х, при которой каждому значению переменной х из определённого множества D соответствует одно определённое значение у, называется функцией от переменной х.
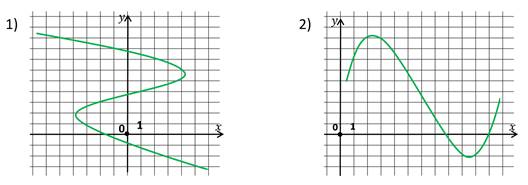
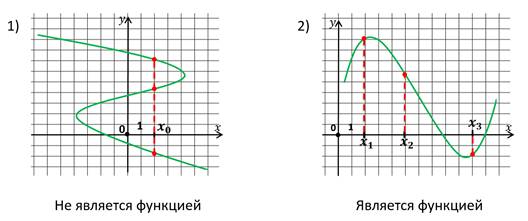
Перед нами графики двух зависимостей.
Мы должны определить, какая из них является функцией, а какая нет. В определении сказано, что только та зависимость является функцией, у которой каждому значению аргумента соответствует единственное значение функции. Давайте посмотрим на первый график.
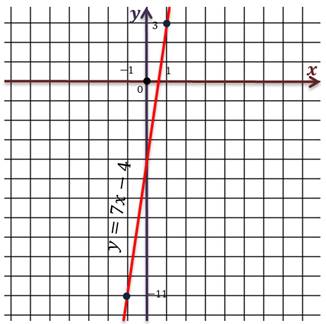
В общем виде любую функцию можно записать так y = f(x). Например, для функции y= 7x – 14 можно записать, что f(x) = 7x – 14, это одно и тоже. Под буквой f понимают некоторый набор действий над переменной x, в данном случае умножение на 7 и вычитание 14.
Переменную x называют независимой или аргументом функции, а y — зависимой (она зависит от x).
Понятно, что функция может принимать различные значения в зависимости от значения аргумента. Найдём значение каждой функции при заданном значении аргумента.
Вы заметили, что в этом задании функции и аргументы названы разными буквами. Действительно, функцию и аргумент можно называть любой буквой латинского или греческого алфавитов.
Сейчас попробуем выяснить, как же получается график функции, и дадим определение этому понятию.
f(1) = 7 · 1 – 4 = 7 – 4 =3
Получаем точку с координатами (1; 3).
Проведём прямую через полученные точки. Мы изобразили график функции y = 7x – 4.
Взяв некоторое x, мы получаем соответствующее y. Эти значения и являются координатами точек графика. Если перебрать все возможные значения x, то мы получим множество точек, изображение которых на координатной плоскости и называют графиком.
Множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — значениям функции, называют графиком функции.
Существует три способа задания функции.
Функция может быть задана формулой.
Например, f(x) = 5x + 1.
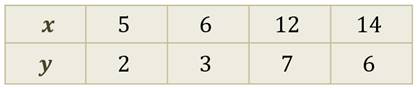
Функция может быть задана таблицей значений аргумента и функции.
Здесь сразу указаны координаты точек графика функции.
Функция можно задать словесно.
Например, каждому натуральному числу x, из отрезка [10; 20], поставлен в соответствие остаток от деления этого числа на пять. Построить график такой функции не составит труда. Для этого составим таблицу значений аргумента и функции.
Аргументами этой функции будут натуральные числа из отрезка от десяти до двадцати. А значениями функции будут остатки от деления соответствующих аргументов на пять.
Теперь давайте поговорим об основных свойствах функции.
Первое свойство о котором мы поговорим – это область определения.
Все значения аргумента, т.е. переменной x образуют область определения функции (пишут D(f)),
Следующее свойство – область значений функции. Все значения зависимой переменной, т.е. y, — область значений функции (пишут E(f)). В скобках указывают букву, которой названа функция.
Область определения можно находить не только по графику функции, но и по формуле, с помощью которой задана функция.
Следующее свойство, которое мы рассмотрим – нули функции.
Значения аргумента, при которых функция принимает значение, равное нулю, называют нулями функции.
В данном случае функция задана графически и мы определили нули функции по графику. Нули функции можно находить по формуле, с помощью которой задана функция.
Стоит обратить внимание на то, что не каждая функция имеет нули.
На графике это будет выглядеть так.
График не пересекает ось икс ни в одной точке.
Теперь поговорим о промежутках знакопостоянства функции.
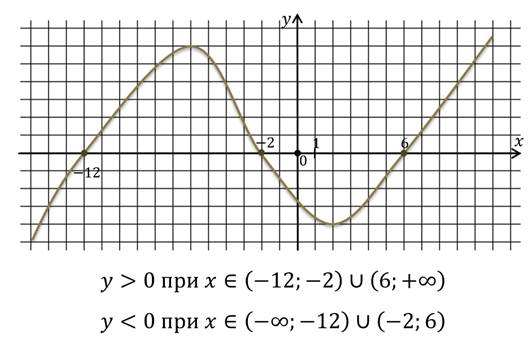
Промежутки знакопостоянства функции — это такие промежутки из области определения, на которых данная функция принимает значения только одного знака, либо положительные, либо отрицательные.
Выполните задание. Запишите промежутки знакопостоянства функции.
Осталось рассмотреть ещё одно свойство. Промежутки монотонности функции.
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции.
Функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
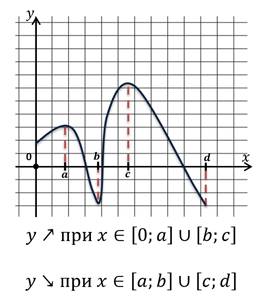
Промежутками монотонности называют такие промежутки из области определения, на которых функция либо возрастает, либо убывает.
Найдём промежутки монотонности данной функции.
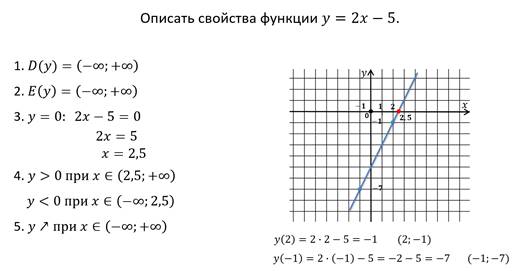
Выполним задание, где нужно описать свойства функции.
Сегодня на уроке мы повторили такие понятия как координатная плоскость, функция, график функции, повторили основные свойства функции.