Что такое область определения функции область значения функции
Определение числовой функции. Область определения функции. Область значения функции.
Что такое область определения функции? что такое область значения функции? Давайте, в этой статье разберемся в понятиях числовой функции и ее характеристиках и свойствах.
Определение функции.
Функция y=f(x) — это когда каждому допустимому значению переменной x соответствует единственное значение переменной y или другими словами такая зависимость переменной y от переменной x.
х — называется независимой переменной или аргументом.
y – называется зависимой переменной или значением функции.
Множество чисел, где x∈X или D(f) — называется областью определения функции. Это множество всех допустимых значений переменной х.
Область значений функций, когда задаем правило или функцию, которая позволяет по произвольно выбранному значению x∈D(f) вычислить соответствующее значение y.
Переменную х или аргумент мы придумываем сами и подставляем в правило, которое задали или функцию. Далее рассчитываем переменную y или значение функции.
В тех диапазонах в которых существует переменная х называется областью определения функции.
В тех диапазонах в которых существует переменная y называется областью значения функции.
Графиком функции y=f(x), x∈X называется множество точек (x; f(x)) координатной плоскости.
Разберём пример №1:
Найдите область определения и область значения числовой функции y=x 2
Вместо переменной x мы можем брать любые числа и просчитать переменную y.
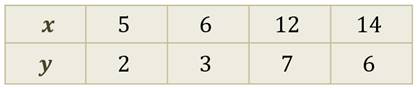
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 16 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 |
По графику также видно, что сколько бы угодно мы не проводили линий через ось х, мы найдем пересечение с графиком.
А теперь рассмотрим переменную у. В таблице мы видим, что переменная y принимает положительные значение, так как и самое минимальное значение 0. Следовательно, y∈[0; +∞).
Если посмотрим на график, то увидим, что графика ниже нуля нет. Следовательно, область значения функции E(f) = [0; +∞).
Разберём пример №2:
Найдите область определения и область значения числовой функции y=x+1?
Вместо переменной x мы можем брать любые числа и просчитать переменную y.
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
По графику также видно, что сколько бы угодно мы не проводили линий через ось х, мы найдем пересечение с графиком.

Рассмотрим переменную у. В таблице мы видим, что переменная y также принимает значения как в положительном, так и в отрицательном направлении. Следовательно, ограничений у переменной y нет, y∈(−∞; +∞). Область значения функции E(f) = (−∞; +∞).
Область определения функции
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие области определения функции
Впервые школьники знакомятся с термином «функция» на алгебре в 7 классе, и с каждой четвертью, с каждой новой темой это понятие раскрывается с новых сторон. И, конечно же, усложняются задачки. Сейчас дадим определения ключевым словам и будем находить область определения функции заданной формулой и по графику.
Если каждому значению x из некоторого множества соответствует число y, значит, на этом множестве задана функция. При этом х называют независимой переменной или аргументом, а у — зависимой переменной или функцией.
Зависимость переменной у от переменной х называют функциональной зависимостью. Записывают так: y = f(x).
Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества.
Из понятия функции сформулируем определение области определения функции.
Область определения функции — это множество всех значений аргумента (переменной x). Геометрически — это проекция графика функции на ось Ох.
Множество значений функции — множество всех значений, которые функция принимает на области определения. Геометрически — это проекция графика функции на ось Оy.
Чтобы обозначить область определения некоторой функции f, используют запись D(f). При этом нужно помнить, что у некоторых функций есть собственные обозначения. Например, у тригонометрических. Поэтому в учебниках можно встретить такие записи: D(sin) — область определения функции синус, D(arcsin) — область определения функции арксинус.
Можно также записать D(f), где f — функция синуса или арксинуса. Если функция f определена на множестве значений x, то можно использовать формулировку D(f) = X. Так, например, для того же арксинуса запись будет выглядеть так: D (arcsin) = [-1, 1].
Область определения можно описывать словами, но часто ответ получается громоздким. Поэтому используют специальные обозначения.
Если мы хотим указать на множество чисел, которые лежат в некотором промежутке, то делаем так:
Например, все действительные числа от 2 до 5 включительно можно записать так:
Все положительные числа можно описать так:
Ноль не положительное число, поэтому скобка возле него круглая.
Области определения основных элементарных функций
Область определения функции — неотъемлемая часть самой функции. Когда мы вводим какую-либо функцию, то сразу указываем ее область определения.
На уроках алгебры мы последовательно знакомимся с каждой функцией: прямая пропорциональность, линейная функция, функция y = x2 и другие. А области их определения изучаем, как свойства.
Рассмотрим области определения основных элементарных функций.
Область определения постоянной функции
Постоянная функция задается формулой y = C, то есть f(x) = C, где C — некоторое действительное число. Ее еще называют константа.
Смысл функции — в том, что каждому значению аргумента соответствует значение, которое равно C. Поэтому, область определения этой функции — множество всех действительных чисел R.
Константная функция — функция, которая для любого элемента из области определения возвращает одно и то же заданное значение. Множество значений такой функции состоит из одного единственного элемента.
Область определения функции с корнем
Функцию с корнем можно определить так: y = n √x, где n — натуральное число больше единицы.
Рассмотрим две вариации такой функции.
Область определения корня зависит от четности или нечетности показателя:
Значит, область определения каждой из функций y = √x, y = 4 √x, y = 6 √x,… есть числовое множество [0, +∞). А область определения функций y = 3 √x, y = 5 √x, y = 7 √x,… — множество (−∞, +∞).
Пример
Найти область определения функции:
Так как подкоренное выражение должно быть положительным, то решим неравенство x 2 + 4x + 3 > 0.
Разложим квадратный трёхчлен на множители:
Дискриминант положительный. Ищем корни:
Значит парабола a(x) = x 2 + 4x + 3 пересекает ось абсцисс в двух точках. Часть параболы расположена ниже оси (неравенство x 2 + 4x + 3 2 + 4x + 3 > 0).
Область определения степенной функции
Область определения степенной функции зависит от значения показателя степени.
Перечислим возможные случаи:
Рассмотрим несколько примеров.
Область определения показательной функции
Область определения показательной функции — это множество R.
Примеры показательных функций:
Область определения каждой из них (−∞, +∞).
Область определения логарифмической функции
Логарифмическая функция выглядит так: y = logax, где где число a > 0 и a ≠ 1. Она определена на множестве всех положительных действительных чисел.
Область определения логарифмической функции или область определения логарифма — это множество всех положительных действительных чисел. То есть, D (loga) = (0, +∞).
Например:
Рассмотрим примеры логарифмических функций:
Область определения этих функций есть множество (0, +∞).
Пример
Укажите, какова область определения функции:
Составим и решим систему:
Область определения тригонометрических функций
Сначала вспомним, как задавать тригонометрические функции и как увидеть их области определения.
Поэтому, если x — аргумент функций тангенс и котангенс, то области определения тангенса и котангенса состоят из всех таких чисел x, что 
Пример
Найдите область определения функции f(x) = tg2x.
Так как a(x) = 2x, то в область определения не войдут следующие точки:
Перенесем 2 из левой части в знаменатель правой части:
В результате 
Ответ: область определения: 
Область определения обратных тригонометрических функций
Вспомним обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккотангенс.
Область определения арктангенса и арккотангенса — все множество действительных чисел R. То есть, D(arctg) = R и D(arcctg) = R.
Таблица областей определения функций
Области определения основных функций в табличном виде можно распечатать и использовать на уроках, чтобы быстрее решать задачки.
И, помните: чем чаще вы практикуетесь в решении задач — тем быстрее все запомните.
Функция
Область определения функции
Что такое функция?
7 класс, 11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие функции
Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.
1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.
Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.
Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у.
2. Функция — это определенное действие над переменной.
Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину у.
В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у. Схематично это выглядит так:
В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях.
3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.
Например, в функции у = 2х каждому действительному числу х ставит в соответствие число в два раза большее, чем х.
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида
область определения выглядит так:
И записать это можно так: D (y): х ≠ 0.
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.
В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению х соответствует одно и только одно значение у. И наоборот — зная у, можно сразу найти х.
Понятие функции. Область определения и область значений функции. Свойства функций
Урок 38. Подготовка к ОГЭ по математике 9 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Понятие функции. Область определения и область значений функции. Свойства функций»
· вспомнить основные сведения о координатной плоскости, функции;
· повторить основные свойства функции.
Начнём мы с вами с координатной плоскости.
Таким образом, мы задали на плоскости прямоугольную систему координат.
Плоскость, на которой задана система координат, называют координатной плоскостью.
Повторим определение функции.
Зависимость одной переменной у от переменной х, при которой каждому значению переменной х из определённого множества D соответствует одно определённое значение у, называется функцией от переменной х.
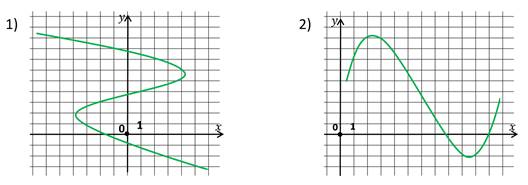
Перед нами графики двух зависимостей.
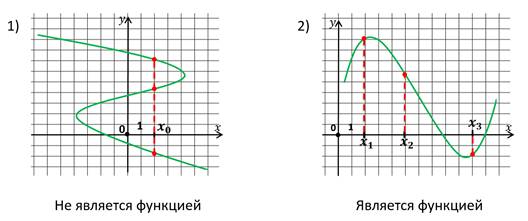
Мы должны определить, какая из них является функцией, а какая нет. В определении сказано, что только та зависимость является функцией, у которой каждому значению аргумента соответствует единственное значение функции. Давайте посмотрим на первый график.
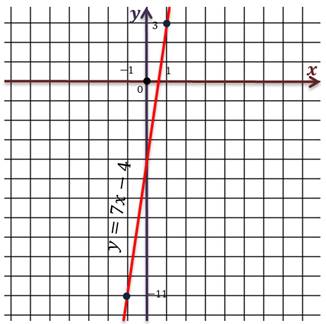
В общем виде любую функцию можно записать так y = f(x). Например, для функции y= 7x – 14 можно записать, что f(x) = 7x – 14, это одно и тоже. Под буквой f понимают некоторый набор действий над переменной x, в данном случае умножение на 7 и вычитание 14.
Переменную x называют независимой или аргументом функции, а y — зависимой (она зависит от x).
Понятно, что функция может принимать различные значения в зависимости от значения аргумента. Найдём значение каждой функции при заданном значении аргумента.
Вы заметили, что в этом задании функции и аргументы названы разными буквами. Действительно, функцию и аргумент можно называть любой буквой латинского или греческого алфавитов.
Сейчас попробуем выяснить, как же получается график функции, и дадим определение этому понятию.
f(1) = 7 · 1 – 4 = 7 – 4 =3
Получаем точку с координатами (1; 3).
Проведём прямую через полученные точки. Мы изобразили график функции y = 7x – 4.
Взяв некоторое x, мы получаем соответствующее y. Эти значения и являются координатами точек графика. Если перебрать все возможные значения x, то мы получим множество точек, изображение которых на координатной плоскости и называют графиком.
Множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — значениям функции, называют графиком функции.
Существует три способа задания функции.
Функция может быть задана формулой.
Например, f(x) = 5x + 1.
Функция может быть задана таблицей значений аргумента и функции.
Здесь сразу указаны координаты точек графика функции.
Функция можно задать словесно.
Например, каждому натуральному числу x, из отрезка [10; 20], поставлен в соответствие остаток от деления этого числа на пять. Построить график такой функции не составит труда. Для этого составим таблицу значений аргумента и функции.
Аргументами этой функции будут натуральные числа из отрезка от десяти до двадцати. А значениями функции будут остатки от деления соответствующих аргументов на пять.
Теперь давайте поговорим об основных свойствах функции.
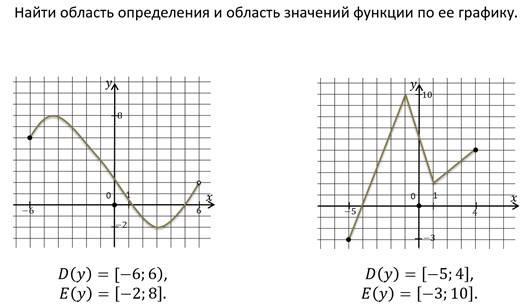
Первое свойство о котором мы поговорим – это область определения.
Все значения аргумента, т.е. переменной x образуют область определения функции (пишут D(f)),
Следующее свойство – область значений функции. Все значения зависимой переменной, т.е. y, — область значений функции (пишут E(f)). В скобках указывают букву, которой названа функция.
Область определения можно находить не только по графику функции, но и по формуле, с помощью которой задана функция.
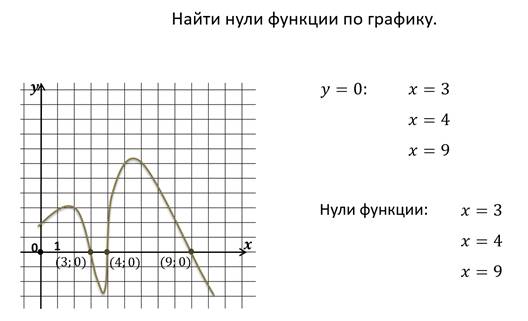
Следующее свойство, которое мы рассмотрим – нули функции.
Значения аргумента, при которых функция принимает значение, равное нулю, называют нулями функции.
В данном случае функция задана графически и мы определили нули функции по графику. Нули функции можно находить по формуле, с помощью которой задана функция.
Стоит обратить внимание на то, что не каждая функция имеет нули.
На графике это будет выглядеть так.
График не пересекает ось икс ни в одной точке.
Теперь поговорим о промежутках знакопостоянства функции.
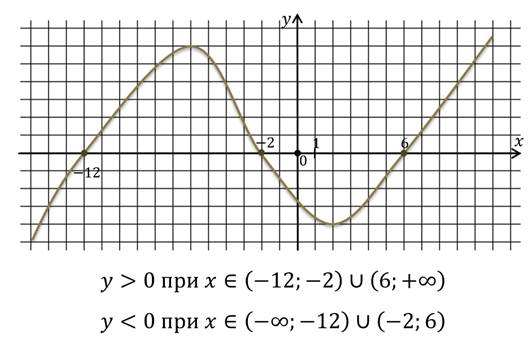
Промежутки знакопостоянства функции — это такие промежутки из области определения, на которых данная функция принимает значения только одного знака, либо положительные, либо отрицательные.
Выполните задание. Запишите промежутки знакопостоянства функции.
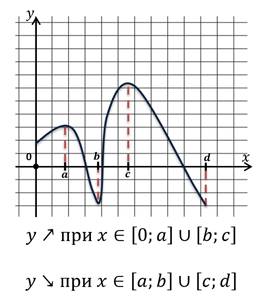
Осталось рассмотреть ещё одно свойство. Промежутки монотонности функции.
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции.
Функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Промежутками монотонности называют такие промежутки из области определения, на которых функция либо возрастает, либо убывает.
Найдём промежутки монотонности данной функции.
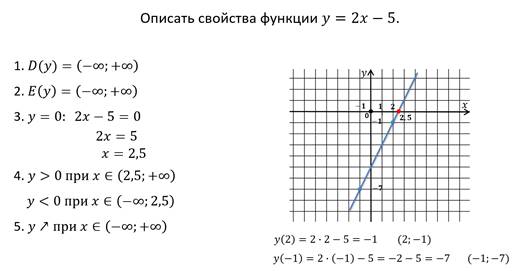
Выполним задание, где нужно описать свойства функции.
Сегодня на уроке мы повторили такие понятия как координатная плоскость, функция, график функции, повторили основные свойства функции.