Что такое область определения выражения с переменной

Область определения функции

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие области определения функции

Впервые школьники знакомятся с термином «функция» на алгебре в 7 классе, и с каждой четвертью, с каждой новой темой это понятие раскрывается с новых сторон. И, конечно же, усложняются задачки. Сейчас дадим определения ключевым словам и будем находить область определения функции заданной формулой и по графику.

Если каждому значению x из некоторого множества соответствует число y, значит, на этом множестве задана функция. При этом х называют независимой переменной или аргументом, а у — зависимой переменной или функцией.

Зависимость переменной у от переменной х называют функциональной зависимостью. Записывают так: y = f(x).

Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества.

Из понятия функции сформулируем определение области определения функции.

Область определения функции — это множество всех значений аргумента (переменной x). Геометрически — это проекция графика функции на ось Ох.

Множество значений функции — множество всех значений, которые функция принимает на области определения. Геометрически — это проекция графика функции на ось Оy.

Чтобы обозначить область определения некоторой функции f, используют запись D(f). При этом нужно помнить, что у некоторых функций есть собственные обозначения. Например, у тригонометрических. Поэтому в учебниках можно встретить такие записи: D(sin) — область определения функции синус, D(arcsin) — область определения функции арксинус.

Можно также записать D(f), где f — функция синуса или арксинуса. Если функция f определена на множестве значений x, то можно использовать формулировку D(f) = X. Так, например, для того же арксинуса запись будет выглядеть так: D (arcsin) = [-1, 1].

Область определения можно описывать словами, но часто ответ получается громоздким. Поэтому используют специальные обозначения.

Если мы хотим указать на множество чисел, которые лежат в некотором промежутке, то делаем так:

Например, все действительные числа от 2 до 5 включительно можно записать так:

Все положительные числа можно описать так:

Ноль не положительное число, поэтому скобка возле него круглая.

Области определения основных элементарных функций

Область определения функции — неотъемлемая часть самой функции. Когда мы вводим какую-либо функцию, то сразу указываем ее область определения.

На уроках алгебры мы последовательно знакомимся с каждой функцией: прямая пропорциональность, линейная функция, функция y = x2 и другие. А области их определения изучаем, как свойства.

Рассмотрим области определения основных элементарных функций.

Область определения постоянной функции

Постоянная функция задается формулой y = C, то есть f(x) = C, где C — некоторое действительное число. Ее еще называют константа.

Смысл функции — в том, что каждому значению аргумента соответствует значение, которое равно C. Поэтому, область определения этой функции — множество всех действительных чисел R.

Константная функция — функция, которая для любого элемента из области определения возвращает одно и то же заданное значение. Множество значений такой функции состоит из одного единственного элемента.

Область определения функции с корнем

Функцию с корнем можно определить так: y = n √x, где n — натуральное число больше единицы.

Рассмотрим две вариации такой функции.

Область определения корня зависит от четности или нечетности показателя:

Значит, область определения каждой из функций y = √x, y = 4 √x, y = 6 √x,… есть числовое множество [0, +∞). А область определения функций y = 3 √x, y = 5 √x, y = 7 √x,… — множество (−∞, +∞).

Пример

Найти область определения функции:

Так как подкоренное выражение должно быть положительным, то решим неравенство x 2 + 4x + 3 > 0.

Разложим квадратный трёхчлен на множители:

Дискриминант положительный. Ищем корни:

Значит парабола a(x) = x 2 + 4x + 3 пересекает ось абсцисс в двух точках. Часть параболы расположена ниже оси (неравенство x 2 + 4x + 3 2 + 4x + 3 > 0).

Область определения степенной функции

Область определения степенной функции зависит от значения показателя степени.

Перечислим возможные случаи:

Рассмотрим несколько примеров.

Область определения показательной функции

Область определения показательной функции — это множество R.

Примеры показательных функций:

Область определения каждой из них (−∞, +∞).

Область определения логарифмической функции

Логарифмическая функция выглядит так: y = log_ax, где где число a > 0 и a ≠ 1. Она определена на множестве всех положительных действительных чисел.

Область определения логарифмической функции или область определения логарифма — это множество всех положительных действительных чисел. То есть, D (loga) = (0, +∞).
Например:

Рассмотрим примеры логарифмических функций:

Область определения этих функций есть множество (0, +∞).

Пример

Укажите, какова область определения функции:

Составим и решим систему:

Область определения тригонометрических функций

Сначала вспомним, как задавать тригонометрические функции и как увидеть их области определения.

Поэтому, если x — аргумент функций тангенс и котангенс, то области определения тангенса и котангенса состоят из всех таких чисел x, что и x ∈ r, x ≠ πk, k ∈ Z соответственно.

Пример

Найдите область определения функции f(x) = tg2x.

Так как a(x) = 2x, то в область определения не войдут следующие точки:

Перенесем 2 из левой части в знаменатель правой части:

В результате . Отразим графически:

Ответ: область определения: .

Область определения обратных тригонометрических функций

Вспомним обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккотангенс.

Область определения арктангенса и арккотангенса — все множество действительных чисел R. То есть, D(arctg) = R и D(arcctg) = R.

Таблица областей определения функций

Области определения основных функций в табличном виде можно распечатать и использовать на уроках, чтобы быстрее решать задачки.

И, помните: чем чаще вы практикуетесь в решении задач — тем быстрее все запомните.

Функция

Область определения функции

Источник

Выражения с переменной. Область определения.

В выражения с переменной могут входить буквы, числа, знаки операции, скобки. Так, 4х + 3, х +2у – 2, (у + 4) : х – выражения с переменными.

Областью определения выражения с переменной называется множество значений переменной, при которых это значение имеет смысл. Если дано выражение с двумя переменными х и у, то областью его определения является множество пар чисел (х, у), при которых это выражение имеет смысл.

Тождества

Два математических выражения называются тождеством, если оно превращается в верное числовое равенство при любых значениях переменных, принадлежащих общей области определения (т.е. при значениях переменных, при которых выражения имеют смысл).

Неравенства с одной переменной. Основные понятия. Равносильные неравенства. Теоремы о равносильных неравенствах, следствия из них.

Предложения 2х+7>10-х, х²+7х g(х) или f(х) 10 и 2х>3 равносильны, так как множества их решений равны и представляют промежуток (2/3; ∞).

Теорема 3.Пусть неравенство f(х)>g(х) задано на множестве Х, h(х) – выражение, определённое на том же множестве. Тогда неравенства f(х)>g(х) и f(х)+ h(х)> g(х)+ h(х) равносильны на множестве Х.

Следствия:

1. Если к обеим частям неравенства f(х)>g(х) прибавить одно и то же число d, то получим неравенство f(х)+ d>g(х)+d, равносильное исходному.

2. если какое-либо слагаемое перенести из одной части в другую, поменяв знак слагаемого на противоположный, то получим неравенство равносильное данному.

Теорема 4. Пусть неравенство f(х)>g(х) задано на множестве Х и h(х) – выражение, определённое на том же множестве и для всех х из множества Х выражение h(х) принимает отрицательные значения. Тогда неравенства f(х)>g(х) и f(х)·h(х) g(х) умножить на одно и то же отрицательное число d и знак неравенства поменять на противоположный, то получим неравенство f(х)·d

Уравнения с двумя переменными. Основные понятия (область определения, решение, множество решений, соотношение между ними).

Равенство f(х; у) = 0 представляет уравнение с двумя переменными.

Решением такого уравнения является пара значений переменных, которая обращает уравнение с двумя переменными в верное равенство.

Если перед нами уравнение с двумя переменными, то в его записи на первое место мы должны поставить х, на второе – у.

Чтобы найти другие пары решений данного уравнения, необходимо одну переменную выразить посредством другой – например, х через у. В результате мы получим уравнение

Если уравнения с двумя переменными имеют одинаковые корни, то такие уравнения называются равносильными.

Для уравнений с двумя переменными справедливы теоремы о равносильных преобразованиях уравнений.

Рассмотрим график уравнения с двумя переменными.

Пусть дано уравнение с двумя переменными f(х; у) = 0. Все его решения можно изобразить точками на координатной плоскости. Это множество точек плоскости и называется графиком уравнения f(х; у) = 0.

Так, графиком уравнения у – х 2 = 0 является парабола у = х 2 ; графиком уравнения у – х = 0 является прямая; графиком уравнения у – 3 = 0 является прямая, параллельная оси х, и др.

Уравнение вида ax + by = c, где x и y – переменные, а a, b и c – числа, называется линейным; числа a, b называются коэффициентами при переменных, с – свободным членом.

Графиком линейного уравнения ax + by = c является:

1. прямая; если хотя бы один из коэффициентов при переменных отличен от нуля;

2. прямая, параллельная оси х, если а = 0;

3. прямая, параллельная оси у, если b = 0.

Если линейное уравнение ax + by = c имеет вид 0 ∙ х + 0 ∙ y = c, то мы должны рассмотреть два случая:

1. с = 0. В таком случае уравнению удовлетворяет любая пара (х; у), а потому графиком уравнения является вся координатная плоскость;

2. с ≠ 0. В таком случае уравнение не имеет решения, значит, его график не содержит ни одной точки.

25. графическое решение неравенств и систем неравенств с двумя переменными.

Предикат вида f₁(х, у)> 0,хÎХ, уÎ У. Решением неравенствас двумя переменными называется пара значений пере­менных, обращающая неравенство в верное числовое неравенство. Известно, что пара действительных чисел(х, у) однозначно определяет точку координатной плос­кости. Это дает возможность изобразить решения неравенства или системы нера­венств с двумя переменными геометрически, в виде некоторого множества точек коорди­натной плоскости. Если уравнение. f(х, у) = 0 определяет некоторую линию на координат­ной плоскости, то множество точек плоско­сти, не лежащих на этой линии, состоит из конечного числа областей С₁,С₂,. С_п (рис. 17.8). В каждой из областей С, функцияf(х, у) отлична от нуля, т.к. точки, в которыхf(х, у) = 0 принадлежат границам этих областей

Уравнение прямой

Общее уравнение прямой— уравнение первой степени относительно пе­ременных х и у, т.е. уравнение вида Ах +Ву + С = 0 при условии, что коэффици­енты А и В одновременно не равны нулю.

Уравнение прямой в отрезкахимеет вид х/а + у/b= 1, гдеа иb- соответственно абсцисса и ордината точек пересечения прямой с осямиОх иОу.

ордината точки пересечения прямой с осьюОу

Угловой коэффициент прямой, проходящей через точкиА и В, находится по формуле

27.Взаимное расположение прямых на плоскости

На плоскости заданы прямые общими уравнениями:

Если выполнены условия , то прямые совпадают.

Если выполнены условия , то прямые параллельны.

Если скалярное произведение векторов и обращается в ноль, т. е. то прямые и перпендикулярны.

Условие перпендикулярности прямых и в координатной форме:

Время и его измерение Промежутки времени можно сравнивать. Промежутки времени можно складывать, вычитать, умножать на положительное действительное число. Промежутки времени измеряют.. Единицей времени должен быть регулярно повторяющийся процесс. Такой единицей в Международной системе единиц названа секунда. Год – это промежуток времени, близкий по продолжительности к периоду обращения Земли вокруг Солнца. Год делится на 12 календарных месяцев разной продолжительности (28, 29, 30, 31 день). В году примерно 365 дней. Различаю: календарный (юлианский, григорианский), лунный, звездный, тропический, драконический, аномалистический. Месяц – это промежуток времени, близкий к периоду обращения Луны вокруг Земли. Месяц делится на 4 недели, в каждой из которых 7 дней. Различают: календарный, звездный, синодический, драконический. Сутки бывают эфемеридные (24 ч = 1440 мин = 86400 с), солнечные, средние солнечные, звездные. Неделя – это единица измерения времени равная 7 суткам. В недели примерно168 часов. Минута (от лат. minutus – «маленький», «мелкий») – это единица измерения времени, которая равна 1/60 части часа, т.е. 60 секундам. Секунда (от лат. secunda divisio – «второе деление») – это единица измерения времени, равная 1/60 минуты. 1 г = 12 мес = 52 недели 1 мес= 4 недели 1 неделя = 7 суток 1 сутки = 24 часа = 1440 минут = 86400 секунд 1 час = 1/24 суток = 60 минут = 3600 секунд 1 минута = 1/1440 суток = 1/60 часа = 60 секунд 1 секунда = 1000 миллисекунд Календарь – система счисления длительных промежутков времени, основанная на периодичности таких явлений природы, как смена дня и ночи, смен фаз Луны, смена времени года. Лунный календарь;Солнечно – лунный календарь;Юлианский календарь («старый стиль»); Григорианский календарь («новый стиль») и др. Прямо пропорциональная зависимость между временем и пройденным рассто­янием обладает свойством: во сколько раз увеличивается (уменьша­ется) время движения, во столько же раз увеличивается (умень­шается) пройденное расстояние. Зависимость расстояния прямолинейного равномерного движения от времени (при постоянной скорости) может быть и линейной, т. е. она может выражаться формулой вида у = kх +b, где k и b — некоторые данные числа Если среди величин S, v, tдве величины — скорость и время — принимают различные значения, а расстояние постоянно, то зависимость между скоростью и временем движения обратно пропорциональная, так как может быть выражена формулой у =k: х, где переменная х есть скорость движения, переменная у — время движения (или наоборот), достояннаяkесть расстояние, которое на­до пройти телу. Обратно пропорциональная зависимость между скоростью и временем движения обладает свойством: во сколько раз увеличивает­ся (уменьшается) скорость движения, во столько же раз уменьшается (увеличивается) время, затраченное на движение. 36. Зависимость между величинами, хар-ми процессы купли-продажи 37. Прямолинейное равномерное движение — это такое движение, при котором за одинаковые промежутки времени, тело проходит одинаковое расстояние. Равномерное движение — это такое движение тела, при котором его скорость остается постоянной ( ),то есть все время движется с одной скоростью, а ускорение или замедление не происходит ( ). Прямолинейное движение — это движение тела по прямой линии, то есть траектория у нас получается — прямая. Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена также, как и перемещение тела. То есть вектор скорости совпадает с вектором перемещения. При всем этом средняя скорость в любой промежуток времени равна начальной и мгновенной скорости: Скорость равномерного прямолинейного движения — это физическая векторная величина, равная отношению перемещения тела за любой промежуток времен к значению этого промежутка t: Из данной формулы. мы легко можем выразить перемещение тела при равномерном движении: 38. Угол – это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Лучи называются сторонами угла, а их общее начало – вершиной угла. Угол называется развёрнутым, если обе его стороны лежат на одной прямой. Можно сказать, что каждая сторона развёрнутого угла является продолжением другой стороны. Угол называется прямым, если он равен 90°, острым, если он меньше прямого угла, т.е. меньше 90°, тупым, если он больше 90°, но меньше 180°, т.е. больше прямого, но меньше развёрнутого угла. Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными. Сумма смежных углов равна 180°. Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого. 39. Треугольником называется геометрическая фигура, которая состоит из трёх тчек, не лежащих на одной прямой, и трёх отрезков, соединяющих эти три точки. Элементы: стороны, углы, высоты,биссектрисы, медианы, средние линии. 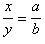Высотойтруегол., опущенной из данной вершины, называется перпендикуляр, проведённый из этой вершины к прямой, содержащей противолежащую сторону. Медианатреугольника — это отрезок, соединяющий верщину треугольника с серединой противолежащей стороны этого треугольника. Свойства : 1.Медиана разбивает треугольник на два треугольника одинаковой площади. 2.Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника. 3.Весь треугольник разделяется своими медианами на шесть равновеликих треугольников. Биссектриса угла — это луч, который исходит из его вершины, проходит между его сторонами и делит данный угол пополам. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника. Свойства 1.Биссектриса угла — это геометрическое место точек, равноудаленных от сторон этого угла. 2.Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилегажащим сторонам: . 3.Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник. Высота Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону этого треугольника. Источник ← Что такое окуляр в микроскопе 5 класс Что такое вертикальная планировка земельного участка → Вам также понравится Что такое батальон в армии кратко 27.10.202312.04.2022 admin 0 Что такое дгк на заправке 27.10.202315.04.2022 admin 0 Что такое органическая еда в америке 25.10.202320.04.2022 admin 0 Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сохранить моё имя, email и адрес сайта в этом браузере для последующих моих комментариев.