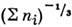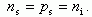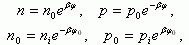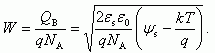Что такое область пространственного заряда

Что такое область пространственного заряда

(3.1)

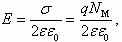
Отметим, что в случае реализации эффекта поля источником внешнего электрического поля могут быть заряды на металлических пластинах вблизи поверхности полупроводника, заряды на границе и в объеме диэлектрического покрытия и т.д.

(3.2)

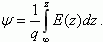
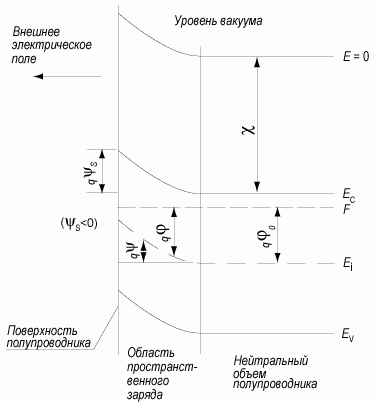
Значение электростатического потенциала на поверхности полупроводника называется поверхностным потенциалом и обозначается ψ_s. На зонной диаграмме (рис. 3.1) величина ψ_s отрицательна.

Рис. 3.1. Зонная диаграмма приповерхностной области полупроводника n-типа

Выразим концентрацию электронов n и дырок p в ОПЗ через электростатический потенциал ψ. В квазинейтральном объеме в невырожденном случае

(3.3)

(3.4)

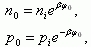
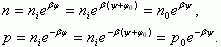
Величины концентраций электронов n_s и дырок p_s на поверхности носят название поверхностной концентрации и имеют значения

(3.5)

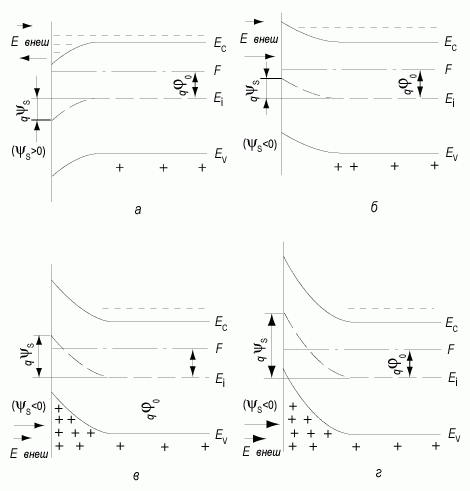
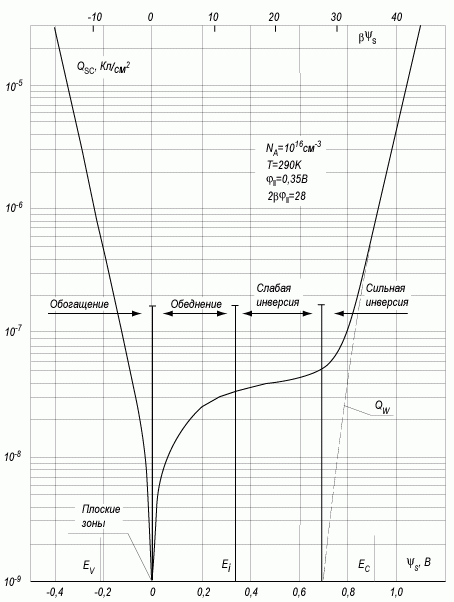
В зависимости от направления и величины внешнего электрического поля, типа полупроводниковой подложки различают 4 различных состояния поверхности полупроводника: обогащение, обеднение, слабая инверсия и сильная инверсия. Все эти ситуации отражены на рисунке 3.2 для полупроводника n-типа.

Переход от состояния обогащения к состоянию обеднения происходит при значении поверхностного потенциала ψ_s = 0, получившем название потенциала «плоских» зон. При этом концентрации основных и неосновных носителей на поверхности и в объеме совпадают.

Переход от области обеднения к области слабой инверсии происходит при значении поверхностного потенциала |ψ_s| = φ₀, соответствующем состоянию поверхности с собственной проводимостью

Рис. 3.2. Зонная диаграмма приповерхностной области полупроводника n-типа при различных состояниях поверхности:
а) обогащение; б) обеднение; в) слабая инверсия; г) сильная инверсия

Переход от области слабой инверсии к области сильной инверсии происходит при значении поверхностного потенциала ψ_s = 2φ₀, получившем название «порогового» потенциала. При этом концентрация неосновных носителей на поверхности равна концентрации основных носителей в объеме полупроводника.

Та область в ОПЗ, где суммарная концентрация свободных носителей электронов и дырок меньше, чем концентрация ионизованной примеси, называется областью обеднения. Область в ОПЗ, где концентрация свободных неосновных носителей больше, чем основных, получила название инверсионного канала.

Источник

Что такое область пространственного заряда

3.2.1. Уравнение Пуассона для ОПЗ

Запишем уравнение Пуассона для полупроводника p-типа:

(3.6)

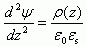
Величина ρ(z) в общем случае, когда отсутствует ограничение на малость возмущения, будет:

(3.7)

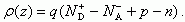
В квазинейтральном объеме, где условие электронейтральности выполняется, ρ(z) = 0.

(3.8)

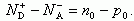
для ρ(z) в ОПЗ имеем:

(3.9)

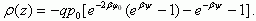
Подставляя (3.9) в (3.6), имеем для нахождения ψ(z) дифференциальное уравнение:

(3.10)

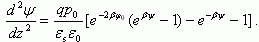
Домножим выражение для дебаевской длины экранирования, которое представлено в разделе 2.5 формулой (2.23), слева и справа на величину dψ/dz. Тогда

(3.11)

(3.12)

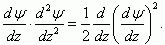
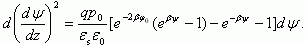
Проинтегрировав (3.12) от бесконечности до некоторой точки ОПЗ, получаем:

(3.13)

(3.14)

(3.15)

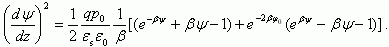
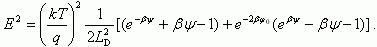
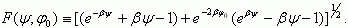
Из (3.14) и (3.15) имеем:

(3.16)

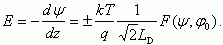
Соотношение (3.16) называется первым интегралом уравнения Пуассона.

Знак электрического поля выбирается в зависимости от знака поверхностного потенциала. Если ψ_s > 0 (обеднение основными носителями или инверсия), поле направлено вглубь полупроводника по оси z и положительно. При ψ_s 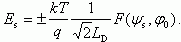(3.17)

Поскольку согласно теореме Гаусса величина электрического поля на поверхности E_s связана определенным образом с плотностью пространственного заряда на единицу площади Q_sc, имеем:

(3.18)

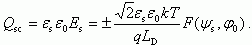
3.2.2. Выражение для заряда в ОПЗ

Выражение (3.18) для заряда в ОПЗ, полученное в предыдущем параграфе, справедливо для любых значений поверхностного потенциала. Однако использование его для конкретных случаев довольно затруднено в силу громоздкости функции F(ψ, φ₀) в виде (3.15). Получим выражение для заряда Q_sc, упростив соотношение (3.18) для различных областей.

Область обогащения (ψ_s 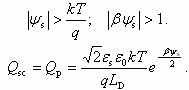(3.19)

Область обеднения (φ₀ > ψ_s > 0). Заряд в ОПЗ Q_sc обусловлен только зарядом ионизованных акцепторов Q_B. Из (3.16, 3.18) следует, что

(3.20)

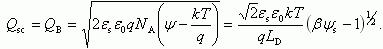
Ширина обедненной области

Область слабой инверсии (2φ₀ > ψ_s > φ₀). Заряд в ОПЗ Q_sc, так же как и в случае обеднения, обусловлен только зарядом ионизованных акцепторов Q_B, поскольку заряд свободных электронов Q_n 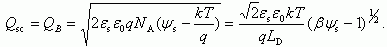(3.21)

Область сильной инверсии (ψ_s > 2φ₀). Заряд в ОПЗ Q_sc обусловлен в основном зарядом свободных электронов вблизи поверхности в инверсионном канале Q_n, хотя в начале области сильной инверсии еще существен вклад заряда ионизованных акцепторов

(3.22)

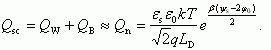
Величина заряда ионизованных акцепторов Q_B в ОПЗ и ширина слоя обеднения W не зависят от поверхностного потенциала ψ_s и равны:

(3.23)

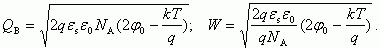
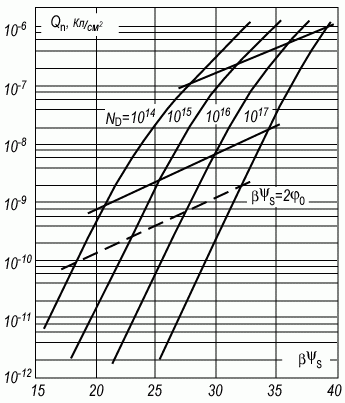
Рис. 3.3. Зависимость заряда в ОПЗ от поверхностного потенциала ψ_s, рассчитанная для кремния p-типа

3.2.3. Избыток свободных носителей заряда

Важной характеристикой ОПЗ является значение заряда свободных носителей (электронов или дырок) Q_p,n или, если выразить этот заряд в единицах элементарного заряда, величина избытка электронов или дырок Γ_p,n в ОПЗ. Определим величину Γ_p как

(3.24)

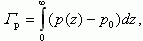
Из (3.24) следует, что

(3.25)

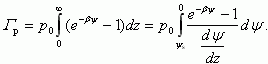
Аналогично избыток электронов Γ_n равен:

(3.26)

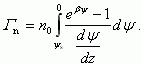
Понятиями избытка Γ_p,n чаще пользуются, когда говорят о свободных носителях в инверсионном канале. Для случая обогащения выражения (3.25, 3.26), рассчитанные с учетом (3.15), при значениях |βψ_s| > 3 будут иметь вид:

(3.27) (3.28)

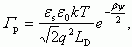
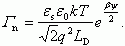
Для области слабой и сильной инверсии выражение для Γ_p,n можно получить в аналитическом виде из выражений для зарядов в ОПЗ, не прибегая к интегрированию (3.25, 3.26).

Действительно, заряд свободных носителей, например, электронов, в инверсионном канале Q_n равен разности полного заряда Q_sc и заряда ионизованных доноров Q_B, для которых имеются аналитические выражения:

(3.29)

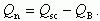
Для случая инверсии соотношение (3.18) для Q_sc упростится и будет иметь вид:

(3.30)

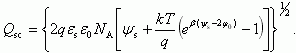
Используя выражения для Q_B в виде (3.20) и (3.23), получаем соответственно для области слабой и сильной инверсии выражения для Q_n в виде:

(3.31) (3.32)

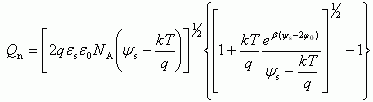
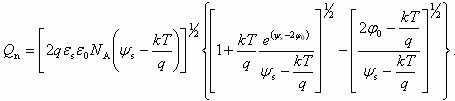
Для случая (3.32), используя соотношение

(3.33)

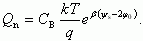
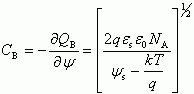
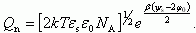
Здесь — емкость обедненной области.

(3.34)

Отметим, что выражение (3.33) совпадает с соответствующим выражением для Q_n в уравнении (3.22). Величина избытка электронов Γ_n = Q_n/q будет для области слабой и сильной инверсии при соответствующих ограничениях равна:

(3.35) (3.36)

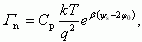
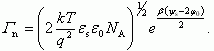
Рис. 3.4. Зависимость заряда свободных электронов Q_n в инверсионном канале от поверхностного потенциала ψ_s, рассчитанная для кремния p-типа с различной концентрацией акцепторов

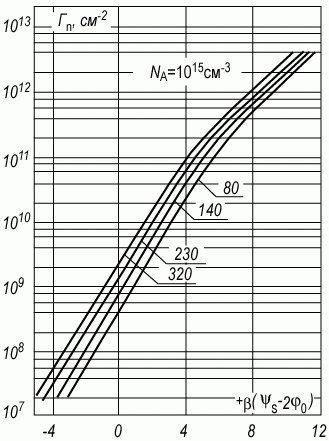
Рис. 3.5. Зависимость избытка электронов Γ_n в инверсионном канале от поверхностного потенциала ψ_s, рассчитанная для кремния p-типа при различной температуре

3.2.4. Среднее расстояние локализации свободных носителей от поверхности полупроводника

Для ряда процессов, протекающих в ОПЗ, важной характеристикой является среднее расстояние λ_c, на котором локализованы свободные носители заряда, электроны или дырки, от поверхности полупроводника. Определим величину λ_c следующим образом:

(3.37)

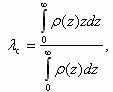
Очевидно, что интеграл

(3.38)

(3.39)

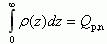
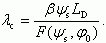
Отметим, что соотношение (3.39) применимо и для случая инверсии, если под λ_c понимать центроид расположения полного заряда Q_sc в ОПЗ.

Для области слабой инверсии электрическое поле E(z) в пределах инверсионного слоя постоянно и равно полю на поверхности E_s. Электростатический потенциал линейно спадает по инверсионному слою:

(3.40)

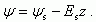
При этом распределение концентрации n(z) по глубине инверсионного слоя будет:

(3.41)

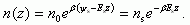
Тогда из (3.39) и (3.41) с учетом (3.4, 3.5) и (3.18) следует:

(3.42)

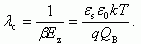
Как следует из (3.42), в области слабой инверсии среднее расстояние λ_c свободных носителей заряда слабо зависит от поверхностного потенциала ψ_s, а следовательно, и от избытка свободных носителей в канале. Зависимость λ_c от температуры T близка к линейной.

Для области очень сильной инверсии, когда Q_n >> Q_B, выражение для центроида электронов в инверсионном канале дается соотношением (3.39). В промежуточной области значений поверхностного потенциала среднее расстояние λ_c необходимо рассчитывать, пользуясь численными методами, по уравнению (3.37).

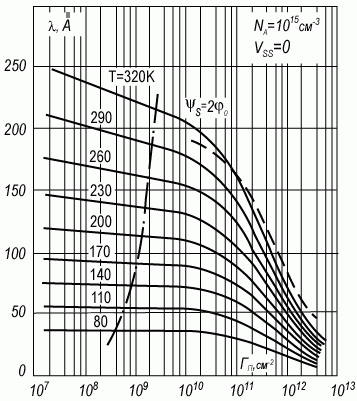
На рисунке 3.6 приведен результат такого численного расчета. Обращает на себя внимание тот факт, что значения центроида λ_c лежат в пределах (20 ÷ 300) A в реально достижимых случаях как для случая обогащения, так и инверсии. Особой точкой является значение потенциала плоских зон ψ_s = 0, где значение λ_c равняется дебаевской длине экранирования, достигающей десятых долей микрона.

Рис. 3.6. Рассчитанное численно среднее расстояние локализации электронов λ_c в ОПЗ в зависимости от избытка электронов Γ_n при разных температурах. Пунктирная линия соответствует самосогласованному квантовому расчету Стерна для многих уровней при T = 300 К для кремния p-типа [2, 21]

3.2.5. Форма потенциального барьера на поверхности полупроводника

При решении уравнения Пуассона в разделе 3.2.1 нами был получен первый интеграл в виде (3.16). Для нахождения формы потенциального барьера, т.е. зависимости электростатического потенциала ψ(z), необходимо проинтегрировать соотношение (3.16) и получить второй интеграл уравнения Пуассона:

(3.43)

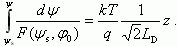
В общем виде уравнение (3.43) решить и найти аналитическое выражение ψ(z) не удается. Рассмотрим частные случаи.

1. Собственный полупроводник: p = n = n_i; φ₀ = 0

Из (3.15) следует, что величина F(ψ, φ₀) для собственного полупроводника

(3.44)

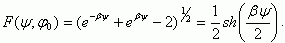
Подставляя (3.44) в (3.43), имеем:

(3.45)

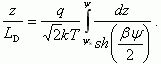
Легко убедиться, что решение (3.45) будет в виде:

(3.46)

(3.47)

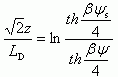
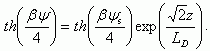
Из (3.47) трудно наглядно представить форму потенциального барьера. Расчет показывает быстрый спад ψ(z) вблизи поверхности и относительно медленное убывание при больших величинах z.

2. Обеднение и слабая инверсия в примесном полупроводнике

Для этой области, как следует из (3.15), функция F(ψ, φ₀) имеет совсем простой вид. Второй интеграл уравнения Пуассона при этом будет равен:

(3.48)

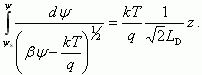
Используя граничное условие, что при z = W, т.е. ширине ОПЗ в обеднении и слабой инверсии потенциала ψ = 0, получаем непосредственным интегрированием:

(3.49)

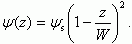
Таким образом, из (3.49) следует, что потенциал ψ в ОПЗ в случае обеднения и слабой инверсии квадратично спадает по глубине ОПЗ. Поскольку толщина инверсионного слоя много меньше ширины обедненной области, то в первом приближении

(3.50)

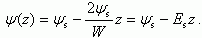
Потенциал ψ в области слабой инверсии спадает по толщине инверсионного слоя по линейному закону, поэтому говорят о треугольной потенциальной яме на поверхности.

3. Область обогащения и очень сильной инверсии в примесном полупроводнике

Будем рассматривать область изменения поверхностного потенциала ψ_s, когда для зарядов в ОПЗ справедливы соотношения (3.19) и (3.22). Получим форму потенциального барьера ψ(z) для случая инверсии, а для случая обогащения вид будет аналогичный.

Из (3.44) и (3.15) следует, что при βψ > 7

(3.51)

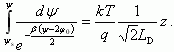
Непосредственное интегрирование (3.51) приводит к зависимости:

(3.52)

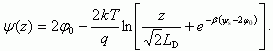
Для случая обогащения аналогично получаем:

(3.53)

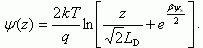
Потенциал ψ(z) в этой области меняется по логарифмическому закону, в таком случае говорят о логарифмической яме на поверхности полупроводника.

Источник

Пространственный заряд

Полезное

Смотреть что такое «Пространственный заряд» в других словарях:

ПРОСТРАНСТВЕННЫЙ ЗАРЯД — (объемный заряд), электрич. заряд, рассредоточенный по нек рому объёму. П. з. определяет пространств. распределение электрич. потенциала и напряжённости электрич. поля. Для возникновения П. з. концентрации положит. и отрицат. носителей заряда… … Физическая энциклопедия

Пространственный заряд — Пространственный заряд распределенный нескомпенсированный электрический заряд одного знака. Пространственные заряды возникают в вакуумных и газоразрядных лампах в пространстве между электродами, а также в неоднородных областях… … Википедия

ПРОСТРАНСТВЕННЫЙ ЗАРЯД — (3) … Большая политехническая энциклопедия

ПРОСТРАНСТВЕННЫЙ ЗАРЯД — (объемный заряд) суммарный электрический заряд свободных электронов и ионов в газе или вакууме. Появление пространственного заряда обычно связано с прохождением электрического тока … Большой Энциклопедический словарь

пространственный заряд — объёмный заряд — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия Синонимы объёмный заряд EN space chargespatial… … Справочник технического переводчика

пространственный заряд — (объёмный заряд), электрический заряд, распределённый по некоторому объёму так, что его плотность конечна. Возникновение пространственного заряда обычно связано с прохождением электрического тока. * * * ПРОСТРАНСТВЕННЫЙ ЗАРЯД ПРОСТРАНСТВЕННЫЙ… … Энциклопедический словарь

пространственный заряд — erdvinis krūvis statusas T sritis Standartizacija ir metrologija apibrėžtis Elektros krūvis, pasiskirstęs tam tikrame vakuumo, dujų, kietojo kūno ar kitokios terpės tūryje. atitikmenys: angl. space charge; volume charge; volumetric charge vok.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

пространственный заряд — erdvinis krūvis statusas T sritis Standartizacija ir metrologija apibrėžtis Erdviniu krūvio tankiu apibūdinamas (elektros) krūvis. atitikmenys: angl. space charge; volume charge; volumetric charge vok. Raumladung, f; Volumenladung, f; Volumladung … Penkiakalbis aiškinamasis metrologijos terminų žodynas

пространственный заряд — erdvinis krūvis statusas T sritis chemija apibrėžtis Laisvųjų krūvininkų el. krūvis erdvėje. atitikmenys: angl. space charge rus. объемный заряд; пространственный заряд … Chemijos terminų aiškinamasis žodynas

пространственный заряд — erdvinis krūvis statusas T sritis fizika atitikmenys: angl. space charge vok. Raumladung, f rus. пространственный заряд, m pranc. charge d’espace, f; charge spatiale, f … Fizikos terminų žodynas

Источник

Пространственный заряд

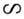
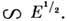
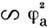
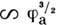
Решение аналогичной задачи для положительных ионов в газе зависит от характера движения ионов (см. Под-вижностъ электронов и ионов). В слабых полях иE в сильных и В первом случае получается j, во втором j . Поля, создаваемые пространственным зарядом в газе, определяют многие важные свойства разряда (временной ход развития разряда, образование стримеров, плазменные колебания и пр.). Образование пространственного заряда влияет на нарастание электронной лавины, распространяющейся в газе высокого давления. В этом случае при превышении определённого числа зарядов в лавине (

10 6 ) пространственный заряд ионов, поле к-рого направлено противоположно внеш. электрич. полю, частично экранирует его и тем самым снижает эффективность размножения носителей в лавине и уменьшает скорость её распространения (см. Лавина электронная).

Пространственный заряд, возникающий при распространении пучка электронов через вакуум, служит причиной угл. расходимости пучка. В результате магн. взаимодействия электронов пучка эффект расходимости с ростом энергии электронов пучка уменьшается. При распространении электронного пучка в газе расходимость также уменьшается в связи с экранирующим действием пространственного заряда положительных ионов.

Поскольку ρ определяется алгебраической суммой зарядов разных носителей, наличие в объёме зарядов противоположных знаков может привести к частичной или полной компенсации пространственного заряда. Примерами могут служить плазма, в которой концентрации ионов и электронов почти равны, и прикатодная область в разряде с накалённым катодом, где положительные ионы практически компенсируют заряд электронов, благодаря чему падение потенциала в таком разряде невелико и почти не зависит от тока.

Уравнение Пуассона, применяющееся в указанных выше случаях, предполагает, что пространственный заряд распределён непрерывно по всему рассматриваемому объёму. В действительности поле пространственного заряда складывается из полей отдельных носителей. Поэтому приведённые зависимости φ и E есть величины, усреднённые для областей, линейные размеры которых велики по сравнению со средним расстоянием между носителями, т. е. с длиной порядка . Хаотически меняющиеся во времени локальные поля должны вычисляться непосредств. наложением полей отдельных носителей с учётом их статистического распределения.

Источник